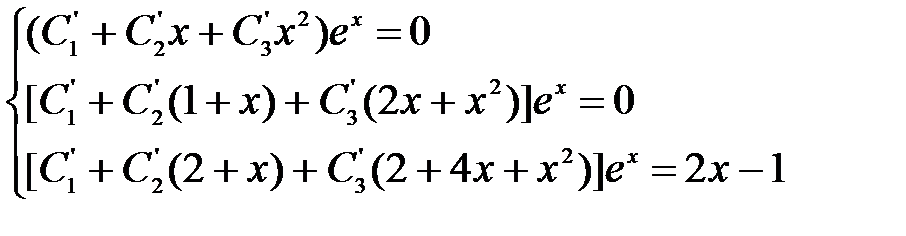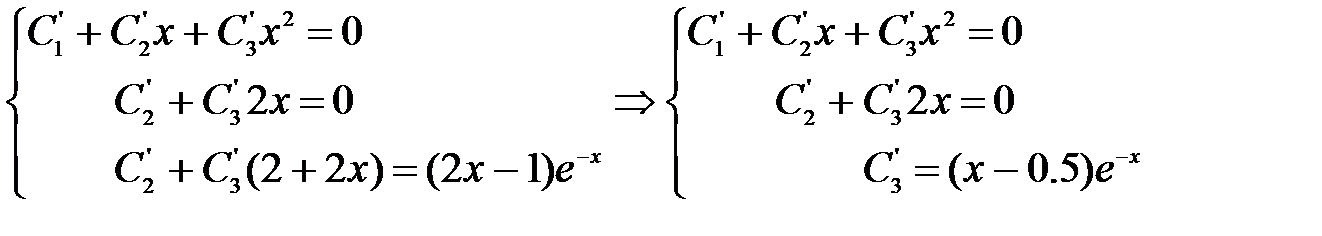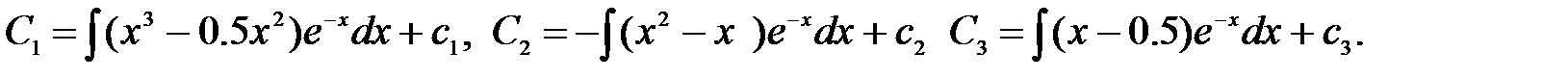§6 Дифференциальные уравнения, допускающие понижение порядка.
1.Пусть дано дифференциальное уравнение вида
y ( n ) = f (x). (19)
Учитывая, что правая часть является функцией только аргумента и, учитывая определение производной n-го порядкаy(n) = [y(n-1)]’, перепишем уравнение в виде:
z’ = f(x), где z(x) = y(n-1) (20)
Дифференциальное уравнение (20) – уравнение первого порядка с разделяющимися переменными. После интегрирования и обратной замены, получим:
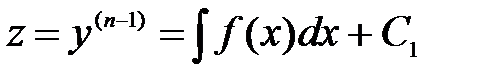 (20)
(20)
Таким образом, в результате такой замены и последующего интегрирования получено дифференциальное уравнение на один порядок ниже. Произведя аналогичную операцию n раз, получим решение уравнения (19):
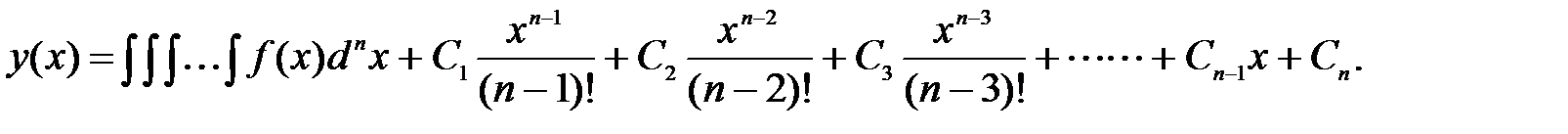
Пример 6.1. 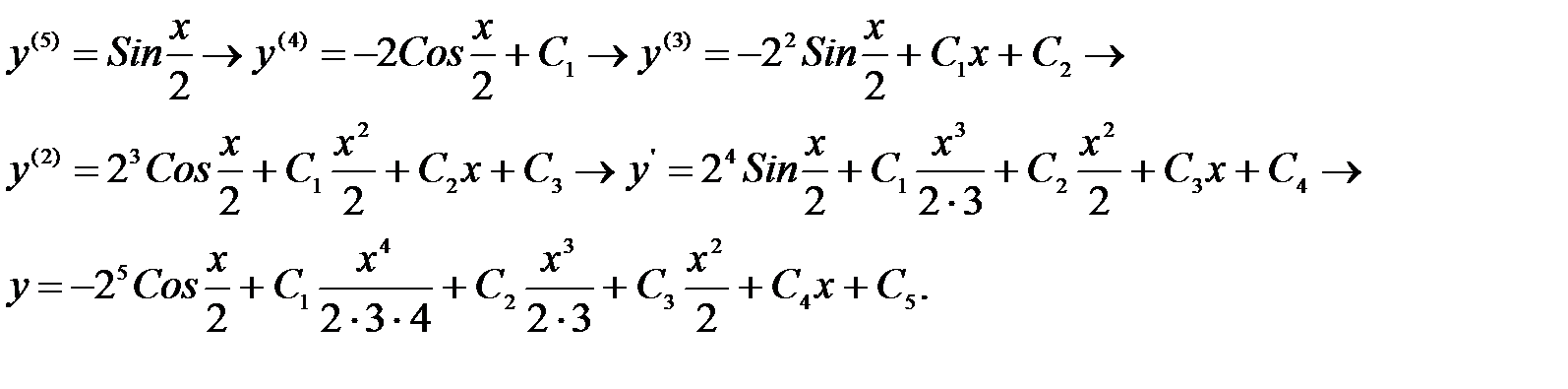
2. Уравнение не содержит независимого переменного:
F(y, y’, y”,………,y(n)) = 0.
В этом случае порядок уравнения может быть понижен на единицу подстановкойy’ = p(y). Правая часть подстановки рассматривается как новая переменная, зависящая от y(x), и, следовательно, все производные  необходимо выразить через производные новой неизвестной функции p(y) поy, дифференцируя функцию p(y) как сложную.
необходимо выразить через производные новой неизвестной функции p(y) поy, дифференцируя функцию p(y) как сложную.
В частности, если уравнение второго порядка F (y, y ’, y ”)=0 не содержит независимой переменной, то указанная замена приводит к уравнению первого порядка. Действительно, дифференцируя подстановку y’=p(y), найдем вторую производную 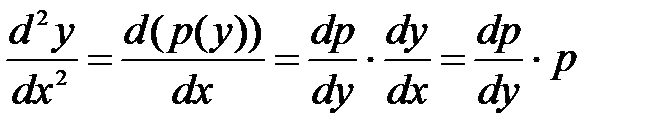 и, произведя замену, получим дифференциальное уравнение первого порядка: F(y, p, p’) = 0.
и, произведя замену, получим дифференциальное уравнение первого порядка: F(y, p, p’) = 0.
Пример 6.2. 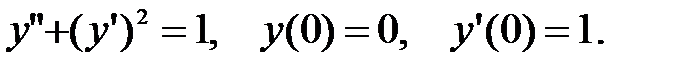 Так как дифференциальное уравнение не содержит независимую переменную, то заменой y’ = p(y), y” = p’p приведем его к виду: p’p + p2 = 1→ p’·p =1 – p2. Полученное уравнение с разделяющимися переменными первого порядка
Так как дифференциальное уравнение не содержит независимую переменную, то заменой y’ = p(y), y” = p’p приведем его к виду: p’p + p2 = 1→ p’·p =1 – p2. Полученное уравнение с разделяющимися переменными первого порядка 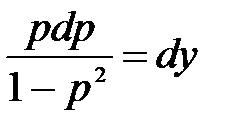 и начальным условием y’(0) = p(0) = 1.Интегрируя уравнение, получим ln|1-p2| = -2y + C1 →|1-p2| = C1e-2y и, после подстановки начального условия и определения произвольного постоянного С1=0, получаем уравнение вида p2 = 1→ p = 1→y’ = 1 с начальным условием y(0) = 0. Его решение y = x + C2,y(0) = 0. Окончательное решение y = x.
и начальным условием y’(0) = p(0) = 1.Интегрируя уравнение, получим ln|1-p2| = -2y + C1 →|1-p2| = C1e-2y и, после подстановки начального условия и определения произвольного постоянного С1=0, получаем уравнение вида p2 = 1→ p = 1→y’ = 1 с начальным условием y(0) = 0. Его решение y = x + C2,y(0) = 0. Окончательное решение y = x.
Пример 6.3. 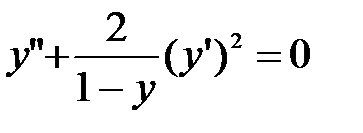 дифференциальное уравнение не зависит от аргумента. Произведем выше указанную замену.
дифференциальное уравнение не зависит от аргумента. Произведем выше указанную замену.  Данное уравнение имеет решение p = 0 или y = C. После сокращения на p, получим дифференциальное уравнение
Данное уравнение имеет решение p = 0 или y = C. После сокращения на p, получим дифференциальное уравнение  решение которогоln|p| = 2ln|y-1| + lnC1→ p=C1(y-1)2. Произведем обратную замену p = dy/dx и придём к уравнению
решение которогоln|p| = 2ln|y-1| + lnC1→ p=C1(y-1)2. Произведем обратную замену p = dy/dx и придём к уравнению  после интегрирования которого,получаем решение дифференциального уравнения →
после интегрирования которого,получаем решение дифференциального уравнения →  или
или 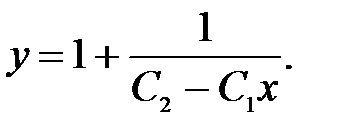
3. Уравнение не содержит искомой функции и ее производных до порядка k -1 включительно:
F(x, y(k), y(k+1), y(k+2),………,y(n)) = 0.
В этом случае порядок дифференциального уравнения может быть понижен до n- k подстановкой y(k) = z(x), y(k+1) = z’(x), y(k+2) = z”(x)…….., y(n)= z(n-k).
В частности, уравнение второго порядка F(x,y’,y”) = 0 подстановкой y’ = z(x), y” = z’(x) сводится к уравнению первого порядка F(x,z,z’) = 0.
Пример 6.3. 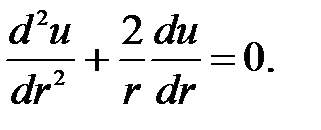 Уравнение не содержит неизвестную функцию u(r). Произведём замену
Уравнение не содержит неизвестную функцию u(r). Произведём замену  Подставим в уравнение и после преобразования получим дифференциальное уравнение
Подставим в уравнение и после преобразования получим дифференциальное уравнение 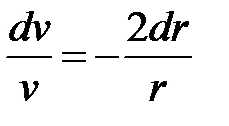 с разделяющимися переменными, решение которого
с разделяющимися переменными, решение которого 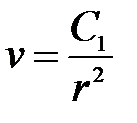 . После обратной замены и интегрирования уравнения найдём искомую функцию
. После обратной замены и интегрирования уравнения найдём искомую функцию 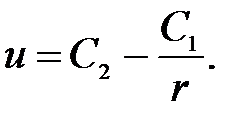
Лекция 5.
§7 Линейные дифференциальные уравнения n–го порядка
Определение. Линейным уравнением n–го называется уравнение линейное относительно неизвестной функции и ее производных и, следовательно, имеет вид
a0(x)y(n)+ a1(x)y(n-1)+ a2(x)y(n-2)+…………+ an-2(x)y”+ an-1(x)y’+ an(x)y= φ(x). (21)
Если φ(x) = 0 (тождественно), то уравнение называется линейным однородным, так как оно однородно относительно неизвестной функции и её производных.
Если коэффициенты ai(x) (i=0.1,2,….,n) непрерывны на некотором отрезке [α,β] и не в одной точке этого отрезка не обращаются в ноль, то, разделив уравнение (21) наa0(x), приведем это уравнение при x, изменяющемся на отрезке [α,β], к виду
y(n)+ p1(x)y(n-1)+p2(x)y(n-2)+…………+pn-2(x)y”+ pn-1(x)y’+ pn(x)y= f(x). (22) 
или
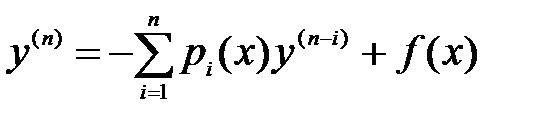 (221)
(221)
Нетрудно показать, что если коэффициенты pi(x) (i=1,2,…..,n) и f(x) непрерывны на отрезке [a,b], то в окрестности любых начальных значений
y(x0)=y0, y’(x0)=y0’, y”(x0)=y0”,…………., y(n-1)(x0)=y0(n-1), где x0 – любая точка интервала (a,b), удовлетворяются условия теоремы существования и
единственности решения уравнения (22).
Пусть задано однородное линейное дифференциальное уравнение
y(n)+ p1(x)y(n-1)+p2(x)y(n-2)+…………+pn-2(x)y”+ pn-1(x)y’+ pn(x)y= 0. (23)
Запишем его кратко в виде
D(y) = 0, (24) где D(y) = y(n)+ p1(x)y(n-1)+p2(x)y(n-2)+…………+pn-2(x)y”+ pn-1(x)y’+ pn(x)y, который будем называть линейным дифференциальным оператором. Оператор D(y) обладает двумя следующими свойствами:
1. Постоянный множитель можно выносить из под знака оператора т.е. D(ky)=k·D(y).
Действительно, D(ky)= (ky)(n)+ p1(x)(ky)(n-1)+…………++ pn-1(x)(ky)’+ pn(x)(ky) = k(y(n)+ p1(x)y(n-1)+p2(x)y(n-2)+…………+pn-2(x)y”+ pn-1(x)y’+ pn(x)y).=k·D(y).
2. Линейный дифференциальный оператор, примененный к сумме двух функций, равен сумме дифференциальных операторов этих функций, т.е. D(y1+ y2)= D(y1)+D(y2). Доказывается аналогично, учитывая свойство производной суммы функций.
Следствие. Дифференциальный оператор, примененный к линейной комбинации функций равен линейной комбинации дифференциальных операторов данных функций. т.е. 
Рассмотрим свойства решений линейных однородных дифференциальных уравнений.
Теорема 7.1. Если y 1 решение уравнения (24), то и произведение постоянного множителя k и этого решения k · y 1 также является решением.
Доказательство. По условию D(y1) = 0. Тогда, учитывая первое свойство дифференциального оператора, получим D(k·y1) = k· D(y1) = k·0 = 0. Свойство доказано.
Теорема 7.2. Если y 1 и y 2, решения уравнения (24), то и их сумма является решением уравнения (24). Доказательство. По условию D(y1) = 0, D(y2) = 0. Тогда, учитывая второе свойство дифференциального оператора, получимD(y1+y2) = D(y1)+ D(y2) = 0. Свойство доказано.
Следствие. Если yi (i =1, 2,…., n) решения уравнения (24), то и их линейная комбинация является решением уравнения (24), т.е. 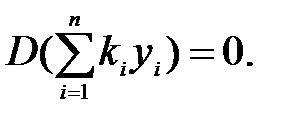
Теорема 7.3. Если линейное однородное уравнение D (y) = 0 с действительными коэффициентами pi (x)имеет комплексное решение y (x)= u (x)+ i · v (x), то действительная часть этого решения u (x) и его мнимая часть v (x) в отдельности являются решениями того же однородного уравнения.
Замечание. Не вдаваясь в подробности теории комплексных чисел и функций отметим, что комплексным числом называется число вида a +i·b, где i= 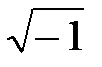 - мнимая единица, a – действительная часть комплексного числа, i·b – мнимая часть комплексного числа, a, b - действительные числа.
- мнимая единица, a – действительная часть комплексного числа, i·b – мнимая часть комплексного числа, a, b - действительные числа.
Комплексная функция действительного аргумента имеет вид - u(x)+i·v(x), где u (x), v (x) - функции действительного аргумента x.
Сформулируем теорему 5.4, необходимую для доказательства теоремы 5.3:
две комплексные функции равны тогда и только тогда, когда равны функции их действительных и мнимых частей соответственно.
В частности, если u (x)+ i · v (x) = 0, то u (x)=0, v (x)=0.
Приведем также формулу Эйлера, связывающую показательное представление комплексного числа и тригонометрическое:
eα+i·β =eα(Cosβ + i·Sinβ) (25)
Доказательство теоремы 5.3. Пусть комплексная функция u(x)+i·v(x) является решением уравнения D(y) = 0, т.е. D(u(x)+i·v(x)) = 0. Тогда, учитывая свойства дифференциального оператора, можно записать D(u(x)+i·v(x)) =D(u(x)) + i· D(v(x)) = 0. Следовательно, согласно теореме 5.4, можем записать D(u(x)) = 0 и D(v(x)) = 0. А это означает, что функции u(x) и v(x) являются решениями линейного однородного уравнения.
Определение. Функции y 1 (x), y 2 (x), y 3 (x),……., yn (x)называются линейно зависимыми на некотором отрезке a ≤ x ≤ b, если существуют постоянные величины α1, α2, α3,………., α n такие, что на том же отрезке
α n · yn (x) + α n · yn (x) + α n · yn (x) + ………..+ α n · yn (x) = 0, (26)
причем, хотя бы одно α i ≠ 0.
Если же тождество (26) справедливо лишь при α1 = α2 =……… = α n = 0, то совокупность функций y 1 (x), y 2 (x), y 3 (x),……., yn (x) называется линейно независимой на том же отрезке.
Укажем некоторые совокупности линейно независимых функций:
а) 1, x, x2, x3, x4,………., xk; b) ek1, ek2, ek3, ………, ekn, (ki≠ kj);
c) Cosα, Sinα, Cos2α, Sin2α, Cos3α, Sin3α,………….,Cosnα, Sinnα.
d) f(x), x f(x), x2 f(x), x3 f(x), x4 f(x),………., xk f(x);
Для определения линейной зависимости или независимости совокупности функций y1(x), y2(x), y3(x),……., yn(x) применяется определитель Вронскогоn-го порядка, состоящего из совокупности функций и их производных до n-1 порядка.
Если определитель Вронского отличен от нуля во всех точках некоторого множества, то совокупностьy1(x), y2(x), y3(x),……., yn(x) функций линейна независима на этом множестве. Если же хотя бы в одной точке обращается в ноль, то - зависима на этом множестве.
Учитывая, что в этом курсе будут рассмотрены дифференциальные уравнения не выше четвертого порядка, укажем более простой признак зависимости совокупности функций y1(x), y2(x), y3(x),……., yn(x).
Если попарное отношение двух функций 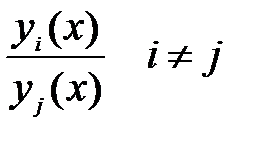 является функцией, то совокупность линейна независима на множестве, а если отношение хотя бы одной пары равна константе(числу), то линейно зависима на этом множестве.
является функцией, то совокупность линейна независима на множестве, а если отношение хотя бы одной пары равна константе(числу), то линейно зависима на этом множестве.
Пример 7.1. Показать, что функции ex, e2x, e3xлинейно независимы. Действительно → 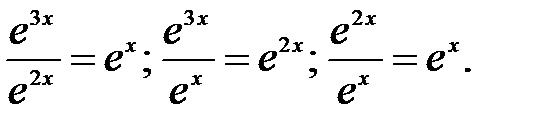 Таким образов, попарные отношения функций – функции и, следовательно, функции ex, e2x, e3x линейно независимы.
Таким образов, попарные отношения функций – функции и, следовательно, функции ex, e2x, e3x линейно независимы.
Пример. Определить зависимость функций – eβx, x·eβx, x2·eβx.
Решение. Найдем попарное отношение функций:  Отношения функций также являются функциями. Следовательно, совокупность функций линейна независима.
Отношения функций также являются функциями. Следовательно, совокупность функций линейна независима.
Лекция 6.
Теорема о структуре общего решения линейного однородного дифференциального уравнения (без доказательства).
Общим решением на множестве x ϵ [ a, b ] линейного однородного дифференциального уравнения
y ( n ) + p 1 (x) y ( n -1) + p 2 (x) y ( n -2) +…………+ pn -2 (x) y ”+ pn -1 (x) y ’+ pn (x) y = 0. с непрерывными на отрезке [ a, b ] коэффициентами pi (x) (i =1,2,3,4,…., n) является линейная комбинация 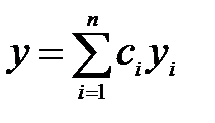 n линейно независимых на том же отрезке частных решений yi (x) (i =1,2,3,4,…., n) с произвольными постоянными коэффициентами.
n линейно независимых на том же отрезке частных решений yi (x) (i =1,2,3,4,…., n) с произвольными постоянными коэффициентами.
Следствие. Из определения следует, что частных решений должно быть ровно столько каков порядок линейного однородного дифференциального уравнения, и они должны быть линейно независимы.
§8. Линейные однородные дифференциальные уравнения
с постоянными коэффициентами
Если в линейном однородном уравнении
a0y(n)+ a1y(n-1)+a2y(n-2)+…………+an-2y”+ an-1y’+ any= 0 (27)
все коэффициенты ai постоянны, то его частные решения могут быть найдены в виде y=ekx, где k – постоянная.
Действительно, подставляя в уравнение (27) y=ekx и y(i) = ki·ekx(i=1,2,…….,n), получим: a0knekx+ a1kn-1ekx+a2kn-2ekx+…………+an-2k2ekx+ an-1kekx+ anekx= 0.
Так как показательная функция не обращается в ноль на всей числовой оси, то, сокращая на ekx, получим алгебраическое уравнение относительно k:
a0kn+ a1kn-1+a2 kn-2 +…………+an-2 k2+ an-1k+ an= 0, (28)
которое называется характеристическим для линейного однородного уравнения с постоянными коэффициентами.
Это уравнение n-ой степени определяет те значения k, при которых y=ekx является решениемисходного линейного однородного дифференциального уравнения с постоянными коэффициентами (27).
Таким образом, если ks– решение уравнения (28), то функция y=eksx есть частное решение уравнения (27).
В дальнейшем будут рассматриваться линейные дифференциальные уравнения второго порядка
a0y” + a1y’ + a2y = 0, (29)
но все результаты и выводы можно распространить и на уравнения n-го порядка.
Характеристическое уравнение для уравнения (29) имеет вид:
a0 k2 + a1k + a2 = 0.
Оно имеет два корня k1 и k2. Рассмотрим три случая вида общего решения уравнения (29) в зависимости от значений корней характеристического уравнения.
1. Корни k1 и k2 действительные и различные k1 ≠ k2. Им отвечают два частных решения y1=ek1x; y2=ek2x. Убедимся, что они линейно независимы
ek1 x/ek2 x= e (k1-k2 x)≠const. Поэтому общее решение, согласно теореме о структуре y= C1y1 + C2y2=C1ek1x+C2ek2x
Пример 8.1. y’” – 2y” – 8y’ = 0. Характеристическое уравнение соответствующее однородному -k3 – 2k2 – 8k = 0 или k(k2 – 2k – 8) = 0. Его решениями будут k1 = 0, k2 = -2, k3 = 4. Тогда общим решением будет y = C1 + C2e-2x + C3e4x.
2. Корни k1 и k2 действительные и одинаковые k1 = k2. Им отвечают два частных решения y1=ek1x; y2=ek2x. Убедимся, что они линейно зависимы
ek1 x/ek2 x= e (k1-k2 x) = e0 = 1= const.Для того чтобы они были независимыми умножим второе решение на аргумент, т.е. y2 = x·y1 = x·ek1x. Убедимся, что эта функция будет решением уравнения (29), учитывая что y1 –частное решение.
Подставим y2 = x·y1 в (29), учитывая y2’= x·y1’+ y1; y2” = x·y1” + 2· y1’ → a0 (x·y1” + 2· y1’)+ a1(x·y1’+ y1) + a2y1 = 0. Учитывая, что a0y1” + a1y1’ + a2y1 = 0 и y1=ek1x, получим ek1x(2k1a0 + a1) = 0. Так как по теореме Виетта 2k1 = -a1/a0.
Таким образом, в случае кратного корня общее решение уравнения (29) имеет вид
y = (C1 + C2x) ekx, где k – корень характеристического уравнения кратности 2.
Если корень кратности p, то ему отвечает решение (C 1 + C 2 x + C 3 x 2 +……+ Cpxp -1) ekp x
Пример 8.2. Найти общее решение уравнения y’”-3y”+3y’-y = 0.
Его характеристическое уравнениеk3- 3k2+3k-1=0 или (k – 1)3=0. Следовательно, k = 1, которому отвечает частное решениеy1=ex. Так как корень кратности 3, то два других частных решения будут y2=x·exy3=x2·ex. Итак, общее решение y = (C1 + C2x + C3x2)ex.
Корни комплексно-сопряженные k1,2 = α ± iβ. Этим корням отвечают два частных решения y1=e(α-iβ) x, y2=e(α+iβ) x. Но если задача решается на множестве действительных чисел, то работа с комплексными числами вызывает определенные трудности, которые можно обойти, применяя формулу Эйлера, так что
e(α-iβ) x = eαxCosβx - ieαxSinβx
e(α+iβ) x = eαxCosβx + ieαxSinβx.
Таким образом, учитывая теорему 7.3, частными решениями будут функции
y1= eαxCosβx, y2 = eαxSinβx, а общим решением - y =eαx(C1·Cosβx+ C2·Sinβx).
Пример 8.3. Решить y” - 6y’+ 13y = 0.
Характеристическое уравнение – k2 – 6k + 13 = 0 → 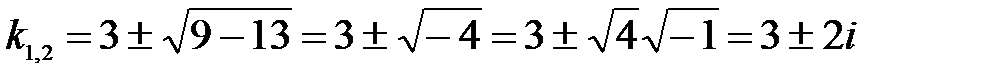 . Итак, частными решениями будут функции y1=e3xCos2x, y2=e3xSin2xи общим - y =e3x(C1Cos2x + C2Sin2x).
. Итак, частными решениями будут функции y1=e3xCos2x, y2=e3xSin2xи общим - y =e3x(C1Cos2x + C2Sin2x).
§9. Неоднородные линейные уравнения высших порядков
Линейным неоднородным дифференциальным уравнением называется уравнение вида:
a0(x)y(n)+ a1(x)y(n-1)+ a2(x)y(n-2)+…………+ an-2(x)y”+ an-1(x)y’+ an(x)y= φ (x)
или, после деления на a 0 (x), если коэффициент a 0 (x) ≠ 0 на отрезке x ϵ [ a, b ] и φ(x)≠0, уравнение:
y ( n ) + p 1 (x) y ( n -1) + p 2 (x) y ( n -2) +…………+ pn -2 (x) y ”+ pn -1 (x) y ’+ pn (x) y = f (x). (30)
Это уравнение, сохраняя прежние обозначения, можно записать в виде:
D(y) = f(x). (31)
Если при всех x ϵ [a,b] коэффициенты уравнения и правая часть непрерывны, то оно имеет единственное решение, удовлетворяющее начальным условиям
y(k)(x0) = y0(k) (k = 1,2,3,………,n-1), где y0(k)- любые действительные числа, а x0 – любая точка интервала (a,b).
Назовём уравнение
D(y) = 0 (32)
однородным, соответствующим неоднородному уравнению (31).
Из двух свойств линейного оператора D(y) непосредственно следуют следующие свойства решений неоднородного уравнения
1) Сумма частного решения y ч неоднородного уравнения и y 0 соответствующего однородного является решением неоднородного уравнения (31).
Доказательство. По условию D(yч) = f(x), а D(y0) = 0. Тогда D(yч+y0) = D(yч)+ D(y0) = f(x). Что и требовалось доказать.
2) Если yi является решением уравнения D(yi) = fi(x) (i=1, 2,…..,k), то y = 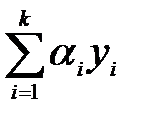 т является решением уравнения (31)
т является решением уравнения (31) 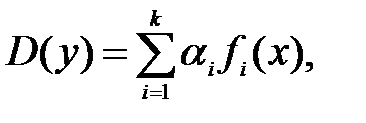 где αi – постоянные.
где αi – постоянные.
Доказательство. По условиюD(yi) = fi(x) 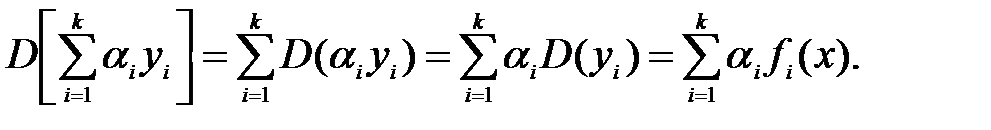 Что и требовалось доказать.
Что и требовалось доказать.
Это свойство еще называется принципом суперпозиции (или наложения) и может быть распространено на случай k→∞
Теорема 9.1(без доказательства). Общее решение на отрезке x ϵ [ a, b ] уравнения D (y) = f (x) с непрерывными на том же отрезке коэффициентами pi (x) и правой частью f (x) равно сумме общего решения соответствующего однородного уравнения (32) и какого-либо частного решения неоднородного уравнения (31), линейно независимого с решениями однородного, т.е.
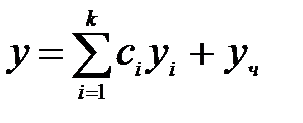 ,
,
где yч – частное решение, yi – частные решения соответствующего однородного уравнения, ci – произвольные постоянные, определяемые из начальных условий.
Лекция 7
§10. Метод вар и ации произвольных постоянных решения
неоднородных линейных дифференциальных уравнений
Метод вариации рассмотрим на примере дифференциального уравнения второго порядка.
Пусть дано уравнение
a0(x)y” + a1(x)y’ + a2(x)y = f(x) (33)
и пусть y = C1y1(x) + C2y2(x) (34)
общее решение соответствующего однородного уравнения a0(x)y” + a1(x)y’ + a2(x)y =0. Положим в этом решении произвольные постоянные функциями C1(x), C2(x), которые необходимо определить,и найдем производную решения (34)
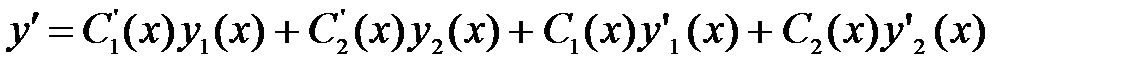
Положим в этом решении первые два слагаемых нулю и, таким образом, получим первое условие для отыскания C1(x) и C2(x):
C1’(x)y1(x) + C2’(x) y2(x) = 0 (35)
Вычислим вторую производную, учитывая равенство (35),
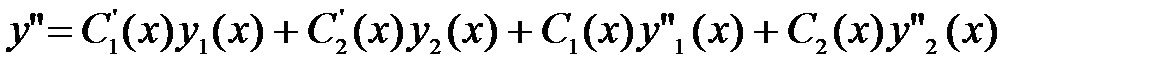
и подставим ее, первую производную и решение в уравнение (33).
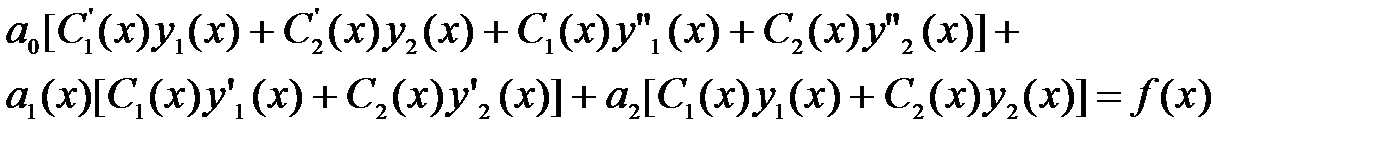
Приведем подобные члены с C1(x) и C2(x) и получим
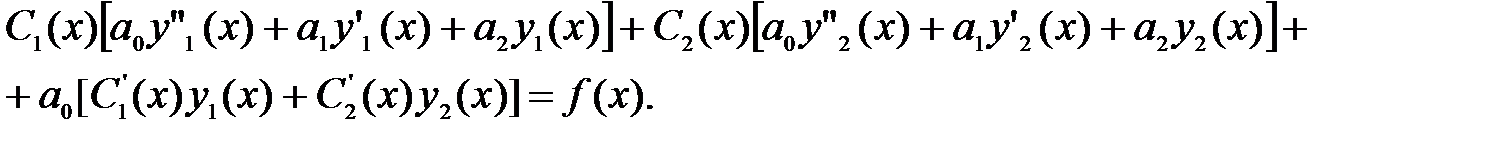
Нетрудно видеть, что первые две квадратных скобки обращаются в ноль, так как y1(x) и y2(x) являются частными решениями однородного уравнения, и в результате получаем второе уравнение для отыскания C1(x), C2(x).
Таким образом, для получения функций C1(x) и C2(x) следует решить систему двух дифференциальных уравнений
C1’(x)y1(x) + C2’(x) y2(x) = 0
C1’(x)y’1(x) + C2’(x) y’2(x) = f(x)/a0.
Результатом решения системы будут два дифференциальных уравнения с разделяющимися переменными, интегрируя которые получим выражения для C1(x) и C2(x)
C1(x) =  C (2x) =
C (2x) = 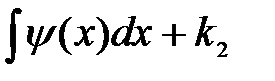 .
.
Подставляя их в решение (35), окончательно получим решение уравнения (33)
y = k1y1(x) + k2y2(x) + y1(x)  + y2(x)
+ y2(x) 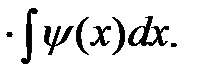
Пример 10.1. Найти общее решение уравнения y” + y = 1/Cosx
1. Решим однородное соответствующее неоднородному y” + y = 0
2. Характеристическое уравнение k2 +1 = 0
3. Корни k = ±iи частные решения y1=Cosx, y2=Sinx
4. Общее решение однородного уравнения y = C1Cosx + C2Sinx
5. Полагаем произвольные постоянные функциямиy = C1(x)Cosx + C2(x)Sinx
6. Составляем систему уравненийC’1Cosx + C’2Sinx = 0 |·Cosx +
-C’1Sinx + C’2Cosx = 1/Cosx |·(-Sinx)
7. Решаем систему и получаем
C’1 = 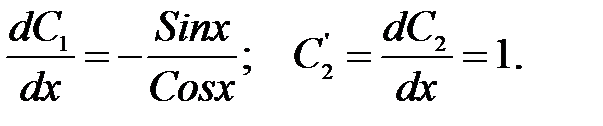 =-
=-
8. Интегрируем и получаем C1(x) =ln(k1|Cosx|); C2(x) = x + k2
9. Подставляем решение однородного уравнения и получаем общее решение неоднородного уравнения
y = Cosx· ln(k1|Cosx|) + Sinx·(x + k2)
Пример 10.2. Найти решение уравнения y’”-3y”+3y’-y = 2x – 1.
Из примера 8.2 решением однородного y’”-3y”+3y’-y = 0 соответствующего неоднородному является функция y = (C1 + C2x + C3x2)ex. Считая произвольные постоянные функциями, составим систему уравнений:
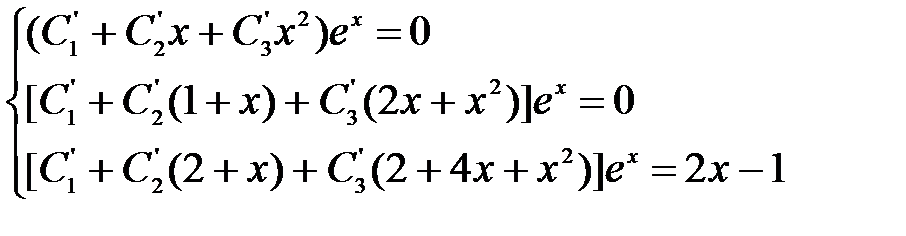
В результате получили систему алгебраических уравнений относительно производных произвольных постоянных. Систему решаем, исключая постоянные, путем вычитания второго уравнения из третьего, первого из второго и, наконец, в полученной системе из третьего – второе.
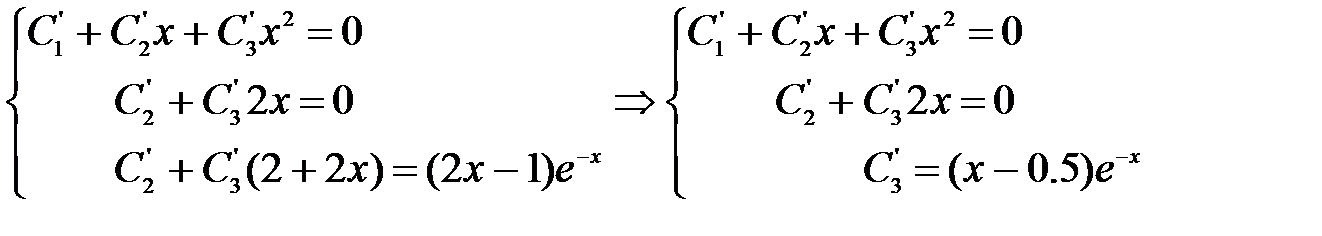
Исключаяиз второго C3’, из первого C3’ и C2’,получим три дифференциальных уравения с разделяющимися переменными:
C1’=(x3 – 0.5x2)e-x, C2’ = - (2x2 – x)e-x, C3’ = (x – 0.5)e-x. Решая эти уравнения найдем выражения произвольных постоянных:
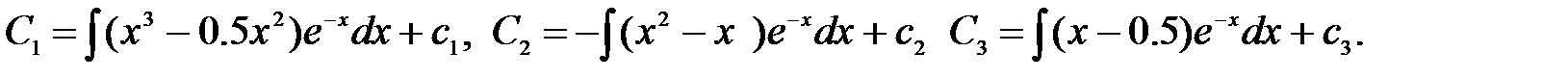
Нетрудно видеть, что вычисление интегралов потребует применение метода интегрирования по частям и, следовательно, достаточно значительного времени. Так для определения C1необходимо три раза применить формулу интегрирования почастям.
Ниже будет приведен метод определения частного решения неоднородного дифференциального уравения с правой частью специального вида, под который подпадает права часть рассмотренного уравения.
§11 Линейные неоднородный уравнения
с постоянными коэффициентами
Решая неоднородные линейныеуравения с постоянными коэффициентами, нередко удается подобрать частные решения и тем самым свести задачу к интегрированию однородного дифференциального уравения.
Пусть заданонеоднородное линейное дифференциальноеуравение с постоянными коэффициентами
a0y(n)+ a1y(n-1)+a2y(n-2)+…………+an-2y”+ an-1y’+ any= f(x) (36)
и пусть функция f(x) имеет вид, называемый специальным:
f(x) = Pn(x)·eαx·(M·Cosβx + N·Sinβx) (37)
или его частные виды как из отдельных сомножителей функции (37), так и различных сочетаний (f(x) = Pn(x), f(x) = eαx, f(x) = M·Cosβx, f(x) = eαx·Sinβx, f(x) = Pn(x)·(M·Cosβx + N·Sinβx) и т.д.)
Функция (37) в общем случае содержит многочлен, показательную функцию и одну или две тригонометрические функции синус и косинус. Причем, все коэффициенты, входящие в многочлен Pn(x) и в функцию (37) (α, β, M, N), имеют числовые значения.
Из теоремы 9.1 следует, что общее решение неоднородного дифференциального уравения состоит из общего решения однородного, соответствующего неоднородному, и какого-либо частного решения неоднородного.
Одним из методов отыскания частного решения в случае правой части функции специального вида является метод неопределенных коэффициентов.
Метод заключается в отыскании частного решения в том виде, в котором задана правая часть, но коэффициенты многочлена и коэффициенты перед тригонометрическими функциями неопределенные. Другими словами коэффициенты не числа, а буквы.
Пример 11.1. Правая часть задана функцией f(x) = (4x3 – 3x)·e4xЭта функция специального вида и ей отвечает частное решение yч = (Ax3 + Bx2 + Cx + D)·e4x. Видно, что многочлен в частном решении записывается по всем степеням, несмотря на то, что в многочлене функции некоторые степени отсутствуют. Показатель экспоненты не меняется.
Пример 11.2. f(x) = 2e4xSin7x. Правой части отвечает частное решение yч = e4x(A·Cos7x + B·Sin7x). В правой части функция зависит от одной тригонометрической функции, а в частном решении обязательно надо записывать сумму тригонометрических функций, так как при дифференцировании функции меняют вид.
Пример 11.3. f(x) = (x2 + 1)·Cos2x +3e2x. В этом случае частное решение записываем в видеyч = (Ax2 + Bx + C)Cos2x + (Dx2 + Ex + F)Sin2x + R·e2x. Так как правая часть уравения состоит из суммы двух функций специального вида, то по второму свойству решений неоднородного дифференциального уравения (принцип суперпозиции) в частом решении записывается сумма функций с неопределенными коэффициентами.
Пример 11.4. f(x) = 5x4 + 3·e5x. →yч = (Ax5 + B x4 + C x3 + D x2 + Ex + F) + Qe5x. В решении многочлен записан по всем степеням и перед экспонентой поставлен многочлен нулевого порядка.
Лекция 8.
§12 Порядок решения линейного неоднородного дифференциального уравения
с функцией специального вида в правой части
1. Решаем однородное дифференциальное уравение соответствующее неоднородному (36) и записываем общее решение:
yо = C1y1+ C2y2+ C3y3+………+ Ciyi+………….+ Cnyn.
2. Записываем частное решениеyч с неопределенными коэффициентами, отвечающее правой части уравения (37)
3. Проверяем линейную независимость частного решения с частными решениями однородного уравения, определяя их отношения yч /yi. Если какое-либо отношение равно постоянной (const), то частное решение умножается на аргумент (x·yч) и вновь проверяем линейную независимость. Процесс продолжается до тех пор пока отношение не станет функцией.
4. Для определения значений неопределенных коэффициентов подставляем частное решение yч в уравнение (36)
5. Приводим подобные члены и приравниваем нулю коэффициенты у функций в полученном равенстве. В результате получаем систему алгебраических уравнений относительно неопределенных коэффициентов.
6. Решаем систему и получаем значения неопределенных коэффициентов
7. Подставляем значения в частное решение и записываем общее решение неоднородного уравения.
Покажем применение метода на примерах.
Пример 12.1 Найти общее решение неоднородного линейного дифференциального уравения y’”-3y”+3y’-y = 2x – 1.
Решение соответствующего однородного получено в примере 10.2 и имеет вид yо = (C1 + C2x + C3x2)ex и состоит из трех частных решений y1 = ex, y2=xex, y2 =x2ex. Записываем частное решение. Так как правая часть является функцией специального вида, а именно многочленом, то и решение записываем в виде многочлена yч = Ax+B. Легко убедиться в линейной независимости yч и yi (i=1,2,3). Найдя предварительно необходимые производныеyч’= A, yч” =0, подставляем yчв уравнение → 3A – (Ax+B)=2x-1→ (A+2)x+(B-3A-1) = 0. Составляем систему алгебраических уравнений: A+2=0, (B-3A-1)=0 и решаем ее. Таким образом, A = -2, B = -5. Итак yч = -2x – 5 и общее решение неоднородногоуравения y = (C1 + C2x + C3x2)ex -2x -5.
Пример 12.2. Решить уравение y” + y’ = 2x2 + 5e-x.
Решение произведем в такой же последовальности, что и выше.
y” + y’ = 0 → k2+k=0 →k(k+1)=0→k1 = 0, k2 = -1→ y1 = e0x=1, y2 = e-x →yo = C1 + C2e-x →Ищем частные решения в виде yч1 =(Ax2+Bx+C), yч2 = De-x.→ Проверяем линейную независимость y1/ yч1=1/C=const, поэтому многочлен умножается на аргумент → yч1 =(Ax2+Bx+C=Ax3+Bx2+Cx.Проверим линейную независимость второго частного решения. Видно, что решения линейно зависимы так какyч2/ y2=De-x/e-x=D=const, поэтому yч2=D·x·e-x. Вычисляем производные частного решения yч = Ax3+Bx2+Cx+ D·x·e-x: y’ч =3Ax2+2Bx+C+ D·e-x - D·x·e-x, y”ч = 6Ax+2B- 2 D·e-x+ D·x·e-x. Подставляем в уравнение и приводим подобные члены 6Ax+2B- 2·D·e-x + D·x·e-x+3Ax2+2Bx+C+ D·e-x - D·x·e-x=2x2 + 5e-x → (3A-2)x2+(6A +2B-0)x+(C-0)-(2D+5)e-x+(D-D)xe-x=0. Чтобы функция в левой части равенства обращалась в ноль необходимо чтобы коэффициенты при функциях обращались в ноль. В результате решения системы уравнений получаем A=2/3, B=-2, C=0, D=-2.5, а частное решение yч= 2x3/3-2x2-2.5·x·e-x. Таким образом, общее решение имеет вид y = C1 + C2e-x+2x3/3-2x2-2.5·x·e-x.
Пример 12.3. Решить уравение y” + 9y = e5x
y” + 9y =0 → k2+9=0 → k=±3i → y1 = Cos3x, y2=Sin3x →yo= C1Cos3x+C2Sin3x
yч = Ae5x. Нетрудно видеть, что функции y1, y2, yч линейно независимы. После подстановки частного решения в уравнение, получим A = 1/34. Общее решение имеет вид y= C1Cos3x+C2Sin3x + e5x/34.
Замечание. В учебных примерах, вообще говоря,если вид функции частного решения не совпадает с видом функций частных решений однородного уравнения, то функции линейно независимы, а если совпадают –линейно зависимы
Пример 12.4 Решить уравение y” + 9y = 12Cos3x.
yo = C1Cos3x+C2 Sin3x. yч = ACos3x +BSin3x.В данном случае функции частных решений и однородного и неоднородного уравнения совпадают, поэтому частное решение неоднородного уравнения умножаем на аргумент → yч = (ACos3x +BSin3x)x. Теперь функции не совпадают (Sin3x ≠ x·Sin3x) и решения линейно независимы. Дифференцируя два раза и подставляя в уравнение вторую производную и частное решение, получим y’ч =(-3ASin3x+3BCos3x)x+ACos3x +BSin3x → y”ч =(-9ACos3x -9BSin3x) +2(-3ASin3x+3BCos3x) → B = 2
Итак, общее решение имеет вид y= C1Cos3x+C2Sin3x + 2xSin3x.
Пример 12.5 Решить уравение y’” –4y’ =9x·ex
y’” – 4y’ = 0 → k3-4k=0 → k(k2-4)=0 → k(k+2)(k-2)=0 → k1=0, k2=-2, k3=2 → y1=1, y2=e-2x, y3=e2x → yo =C1+ C2e-2x+ C3e2x → yч =(Ax+B)ex. Следуя замечанию частное ре


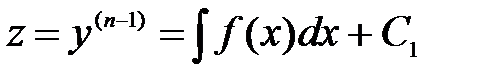 (20)
(20)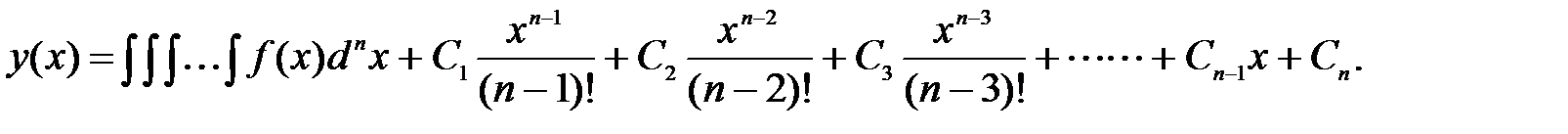
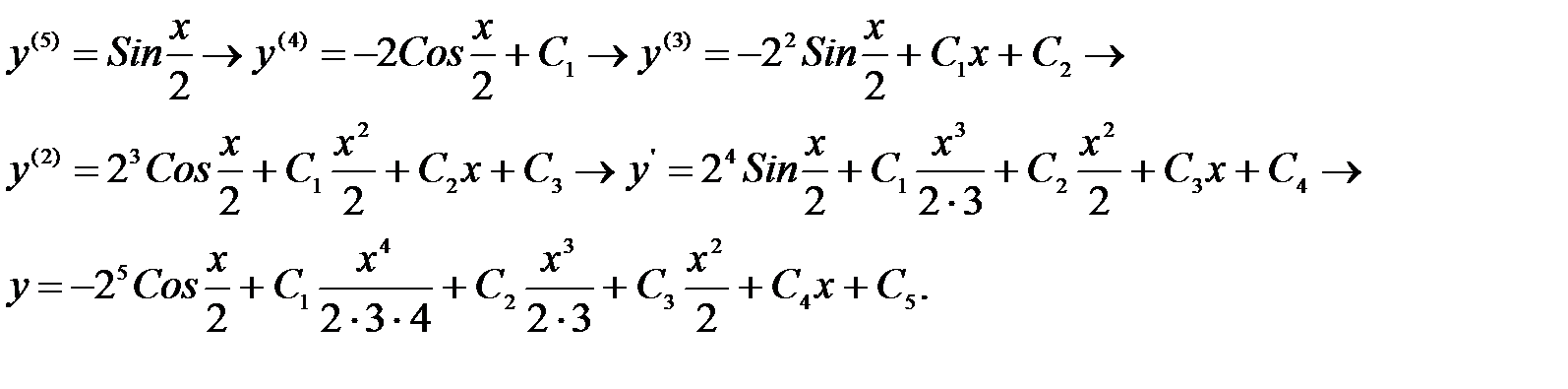
 необходимо выразить через производные новой неизвестной функции p(y) поy, дифференцируя функцию p(y) как сложную.
необходимо выразить через производные новой неизвестной функции p(y) поy, дифференцируя функцию p(y) как сложную.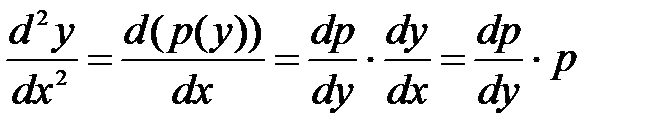 и, произведя замену, получим дифференциальное уравнение первого порядка: F(y, p, p’) = 0.
и, произведя замену, получим дифференциальное уравнение первого порядка: F(y, p, p’) = 0.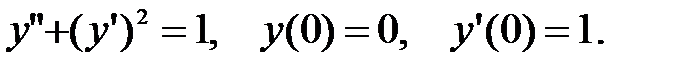 Так как дифференциальное уравнение не содержит независимую переменную, то заменой y’ = p(y), y” = p’p приведем его к виду: p’p + p2 = 1→ p’·p =1 – p2. Полученное уравнение с разделяющимися переменными первого порядка
Так как дифференциальное уравнение не содержит независимую переменную, то заменой y’ = p(y), y” = p’p приведем его к виду: p’p + p2 = 1→ p’·p =1 – p2. Полученное уравнение с разделяющимися переменными первого порядка 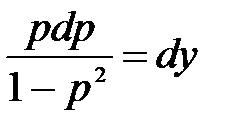 и начальным условием y’(0) = p(0) = 1.Интегрируя уравнение, получим ln|1-p2| = -2y + C1 →|1-p2| = C1e-2y и, после подстановки начального условия и определения произвольного постоянного С1=0, получаем уравнение вида p2 = 1→ p = 1→y’ = 1 с начальным условием y(0) = 0. Его решение y = x + C2,y(0) = 0. Окончательное решение y = x.
и начальным условием y’(0) = p(0) = 1.Интегрируя уравнение, получим ln|1-p2| = -2y + C1 →|1-p2| = C1e-2y и, после подстановки начального условия и определения произвольного постоянного С1=0, получаем уравнение вида p2 = 1→ p = 1→y’ = 1 с начальным условием y(0) = 0. Его решение y = x + C2,y(0) = 0. Окончательное решение y = x. 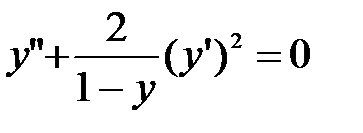 дифференциальное уравнение не зависит от аргумента. Произведем выше указанную замену.
дифференциальное уравнение не зависит от аргумента. Произведем выше указанную замену.  Данное уравнение имеет решение p = 0 или y = C. После сокращения на p, получим дифференциальное уравнение
Данное уравнение имеет решение p = 0 или y = C. После сокращения на p, получим дифференциальное уравнение  решение которогоln|p| = 2ln|y-1| + lnC1→ p=C1(y-1)2. Произведем обратную замену p = dy/dx и придём к уравнению
решение которогоln|p| = 2ln|y-1| + lnC1→ p=C1(y-1)2. Произведем обратную замену p = dy/dx и придём к уравнению  после интегрирования которого,получаем решение дифференциального уравнения →
после интегрирования которого,получаем решение дифференциального уравнения →  или
или 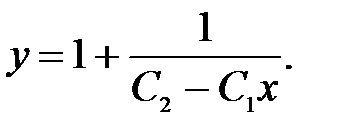
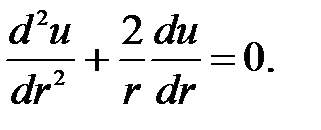 Уравнение не содержит неизвестную функцию u(r). Произведём замену
Уравнение не содержит неизвестную функцию u(r). Произведём замену  Подставим в уравнение и после преобразования получим дифференциальное уравнение
Подставим в уравнение и после преобразования получим дифференциальное уравнение 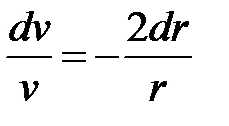 с разделяющимися переменными, решение которого
с разделяющимися переменными, решение которого 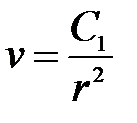 . После обратной замены и интегрирования уравнения найдём искомую функцию
. После обратной замены и интегрирования уравнения найдём искомую функцию 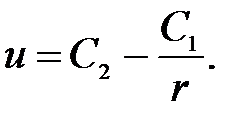

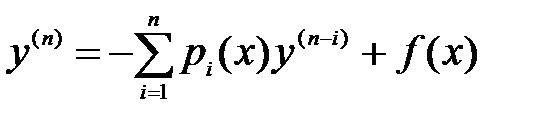 (221)
(221)
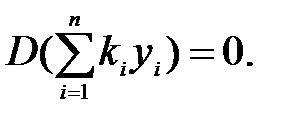
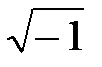 - мнимая единица, a – действительная часть комплексного числа, i·b – мнимая часть комплексного числа, a, b - действительные числа.
- мнимая единица, a – действительная часть комплексного числа, i·b – мнимая часть комплексного числа, a, b - действительные числа.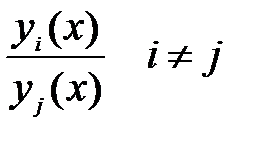 является функцией, то совокупность линейна независима на множестве, а если отношение хотя бы одной пары равна константе(числу), то линейно зависима на этом множестве.
является функцией, то совокупность линейна независима на множестве, а если отношение хотя бы одной пары равна константе(числу), то линейно зависима на этом множестве.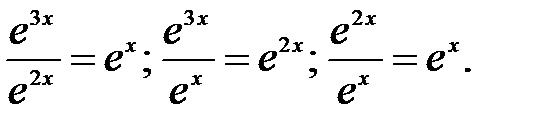 Таким образов, попарные отношения функций – функции и, следовательно, функции ex, e2x, e3x линейно независимы.
Таким образов, попарные отношения функций – функции и, следовательно, функции ex, e2x, e3x линейно независимы. Отношения функций также являются функциями. Следовательно, совокупность функций линейна независима.
Отношения функций также являются функциями. Следовательно, совокупность функций линейна независима.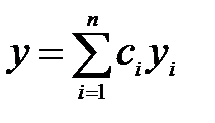 n линейно независимых на том же отрезке частных решений yi (x) (i =1,2,3,4,…., n) с произвольными постоянными коэффициентами.
n линейно независимых на том же отрезке частных решений yi (x) (i =1,2,3,4,…., n) с произвольными постоянными коэффициентами.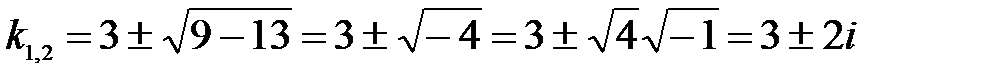 . Итак, частными решениями будут функции y1=e3xCos2x, y2=e3xSin2xи общим - y =e3x(C1Cos2x + C2Sin2x).
. Итак, частными решениями будут функции y1=e3xCos2x, y2=e3xSin2xи общим - y =e3x(C1Cos2x + C2Sin2x).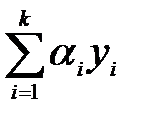 т является решением уравнения (31)
т является решением уравнения (31) 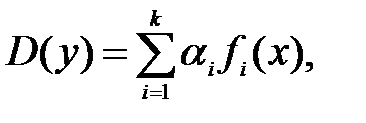 где αi – постоянные.
где αi – постоянные.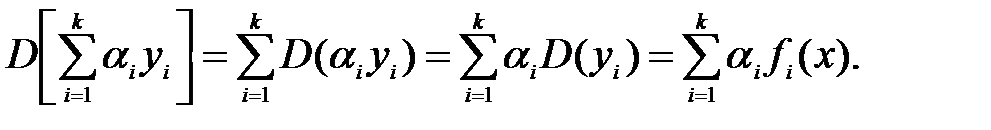 Что и требовалось доказать.
Что и требовалось доказать. 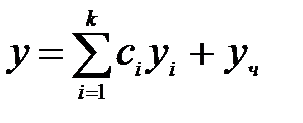 ,
,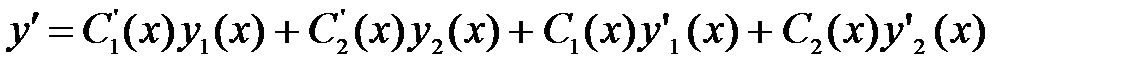
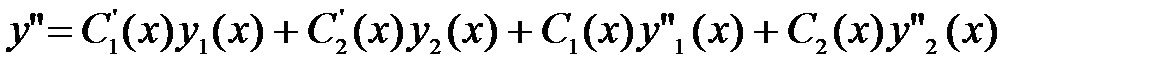
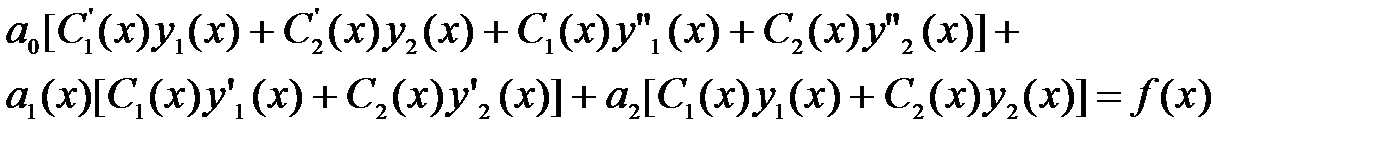
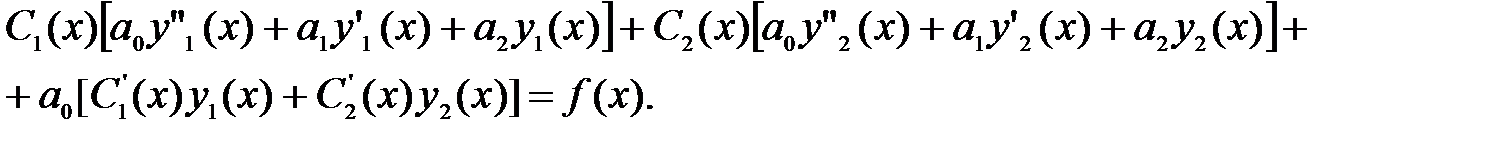
 C (2x) =
C (2x) = 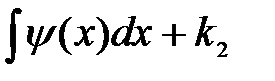 .
. + y2(x)
+ y2(x) 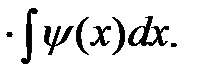
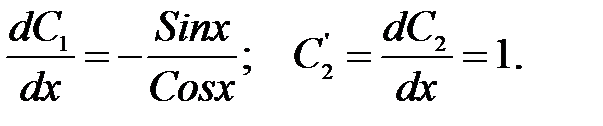 =-
=-