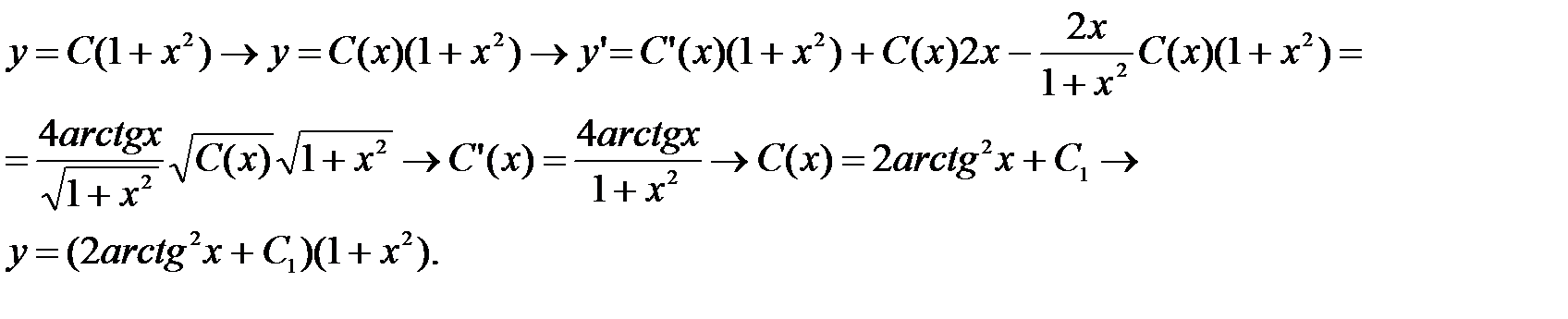переменными
Определение. Дифференциальные уравнения вида f (x) dx = φ(y) dy (7) называются дифференциальными уравнениями с разделенными переменными.
Так как правая часть уравнения (7) зависит только от переменной y, а левая - от переменной x, то уравнение (7) можно проинтегрировать и, тем самым, получить решение дифференциального уравнения: 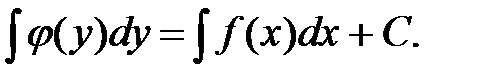
Если из решения не представляется возможным выразить функцию через независимую переменную, то общее решение называется общим интегралом.
Пример 2.1. Найти решение дифференциального уравнения 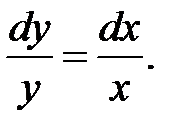 Так как уравнение с разделенными переменными, то интегрируя
Так как уравнение с разделенными переменными, то интегрируя 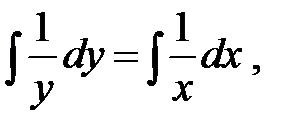 получим
получим
lny = lnx + lnC или, учитывая действия с логарифмами, окончательно имеем y = Cx.
Определение. Дифференциальные уравнения вида P (x, y) dx + Q (x, y) dy =0 (8) называются дифференциальными уравнениями с разделяющимися переменными, если коэффициенты P (x, y) и Q (x, y) можно представить в виде произведения или частного двух функций, каждая из которых зависит только от одной переменной, а именно P (x, y) = P 1 (x) P 2 (y), Q (x, y) = Q 1 (x) Q 2 (y). (9)
Дифференциальные уравнения с разделяющимися переменными с помощью арифметических действий деления и умножения приводятся к дифференциальным уравнениям с разделенными переменными.
Действительно, заменяя коэффициенты при дифференциалах в (8) их выражениями (9), получим
P 1 (x) P 2 (y) dx + Q 1 (x) Q 2 (y) dy = 0 (10)
Равенство (10) разделим на произведение Q 1 (x) P 2 (y) –
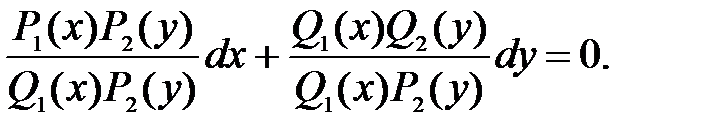
Теперь, сократив одинаковые функции в каждом слагаемом и перенеся одно из них в правую часть равенства, получим дифференциальное уравнение с разделенными переменными:
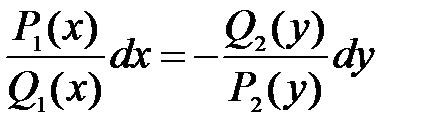 .
.
Таким образом, выше изложен алгоритм решения дифференциальных уравнений с разделяющимися.
Замечание. Д ифференциальное уравнение первого порядка называется дифференциальным уравнением с разделяющимися переменными, если его можно привести к виду y’ = f(x)·φ(y) (11)
Пример 2.2. Решить задачу Коши (найти решение дифференциального уравнения, удовлетворяющего начальным условиям), если 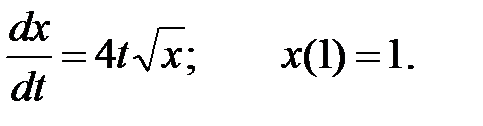
Заданное уравнение уже имеет вид уравнения (11). Поэтому, умножив его на dt и разделив на  , приведем его к уравнению с разделенными переменными:
, приведем его к уравнению с разделенными переменными: 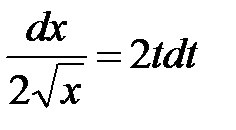 и после интегрирования получим общее решение
и после интегрирования получим общее решение 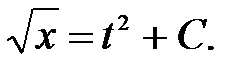 Удовлетворяя начальным условиям, т.е. подставляя в решение t=1, x=1, найдем значение произвольной постоянной: 1 =1 + С, С = 0.
Удовлетворяя начальным условиям, т.е. подставляя в решение t=1, x=1, найдем значение произвольной постоянной: 1 =1 + С, С = 0.
Таким образом, частное решение принимает вид: 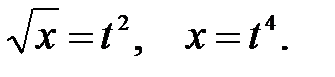
Пример 2.3. Найти решение дифференциального уравнения: 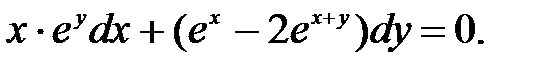
Преобразуем уравнение, учитывая действия со степенями, и вынесем одинаковый сомножитель за скобки второго слагаемого 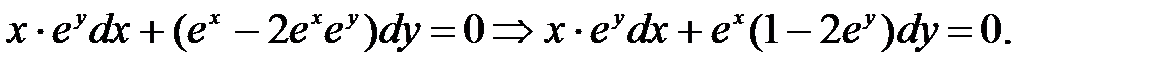 Полученное уравнение подпадает под определение дифференциального уравнения с разделяющимися переменными. Разделяя переменные,получим
Полученное уравнение подпадает под определение дифференциального уравнения с разделяющимися переменными. Разделяя переменные,получим 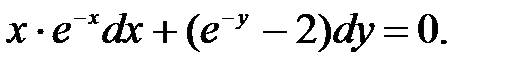 Первое слагаемое интегрируем по частям, принимая u = x, dv = e-x. В результате получим решение e-x(1+x) = e-y+2y+C.
Первое слагаемое интегрируем по частям, принимая u = x, dv = e-x. В результате получим решение e-x(1+x) = e-y+2y+C.
§3 Однородные дифференциальные уравнения первого порядка
Определение. Дифференциальное уравнение называется однородным, если оно имеет вид y ’ = 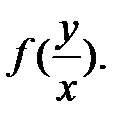 (12)
(12)
Уравнение (12) приводится к уравнению с разделяющимися переменными заменой y = u·x (13) Определим производную замены (13) y’ = u’x + u (14) и подставим выражения (13,14) в уравнение (12) u’x + u = f(u). Учитываяu’ = du/dx, после преобразования получим дифференциальное уравнение с разделяющимися переменными: 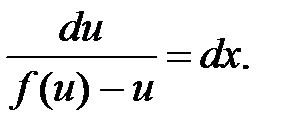
Определение. Функция M (x, y) называется однородной n порядка, если при замене переменных x = x · t, y = y · t выполняется равенство M (xt, yt) = tnM (x, y).
Заметим, что правая часть уравнения (12), является однородной функцией нулевого порядка. Поэтому дифференциальное уравнение
P(x,y)dx + Q(x,y)dy=0
будет однородным, если функции P (x, y), Q (x, y) однородные одного порядка.
Пример 3.1. Уравнение xy3(x2+xy+y2)dx + y2(x4 – y4)dy = 0 является однородным, так как P(xt,yt) = xt(yt)3[(xt)2+ (xt)(yt) + (yt)2] = t6[xy3(x2+xy+y2)] = t6P(x,y), Q(xt,yt) = (yt)2[(xt)4-(yt)4] = t6y2 (x4 – y4) = t4Q(x,y). Таким образом, обе функции являются однородными шестого порядка, а дифференциальное уравнение – однородным.
Замечание 1. Если коэффициенты P (x, y), Q (x, y) являются многочленами и однородными функциями, то для приведения уравнения к виду (12) следует уравнение разделить на аргумент в степени порядка однородности.
В последнем примере, разделив на x6, получим 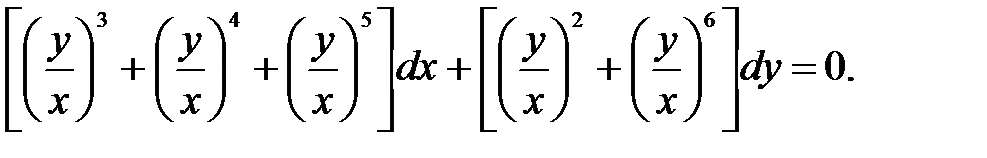
Замечание 2. Если в дифференциальное уравнение входят функции, аргументом которых является отношение переменных (у/х или х/у), то оно также может быть однородным.
Пример 3.2. Уравнение tdx – (t·ex/t+x)dt = 0 может быть однородным, так как аргумент экспоненты – отношение переменных. И в этом случае разделим уравнение на аргумент высшей степени и получим после преобразования 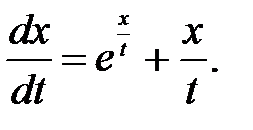 Найдем решение этого уравнения, произведя замену x = t·u,
Найдем решение этого уравнения, произведя замену x = t·u, 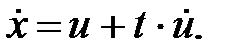 Полученное после преобразований уравнение
Полученное после преобразований уравнение 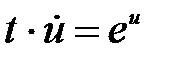 - уравнение с разделяющимися переменными. Разделяя переменные
- уравнение с разделяющимися переменными. Разделяя переменные 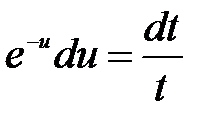 и интегрируя, получим общее решение
и интегрируя, получим общее решение 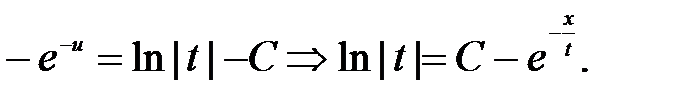
Замечание 3 Дифференциальное уравнение вида  приводится к однородному заменойX = x-x1 и Y = y-y1,гдеx1, y1- решение системы уравнений
приводится к однородному заменойX = x-x1 и Y = y-y1,гдеx1, y1- решение системы уравнений  В результате подстановки дифференциальное уравнение принимает вид
В результате подстановки дифференциальное уравнение принимает вид 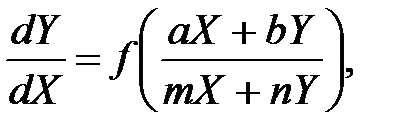 правая часть которого является однородной функцией нулевого порядка.
правая часть которого является однородной функцией нулевого порядка.
Пример 3.3. Найти решение уравнения 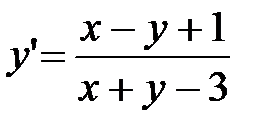 . Найдем точку пересечения двух прямых x-y+1=0 и x+y-3=0.Координаы точки пересечения будут x1=1, y=2. Полагая X=x-1, Y=y-2 и подставляя в дифференциальное уравнение, получим
. Найдем точку пересечения двух прямых x-y+1=0 и x+y-3=0.Координаы точки пересечения будут x1=1, y=2. Полагая X=x-1, Y=y-2 и подставляя в дифференциальное уравнение, получим  Произведя замену Y = uX, Y’ = u +u’X, получим
Произведя замену Y = uX, Y’ = u +u’X, получим  или, разделяя переменные -
или, разделяя переменные - 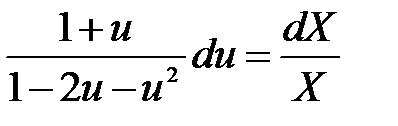 или
или 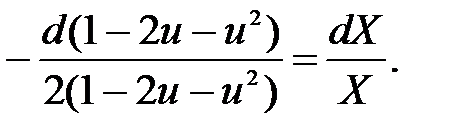 В результате интегрирования получаем общее решение C = X(1-2u-u2) или
В результате интегрирования получаем общее решение C = X(1-2u-u2) или 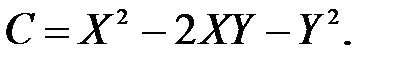 Произведя вторую обратную замену и проведя необходимые преобразования, получим окончательное общее решение x2-2xy-y2+2x+6y = C1.
Произведя вторую обратную замену и проведя необходимые преобразования, получим окончательное общее решение x2-2xy-y2+2x+6y = C1.
Лекция 3.
§4 Линейные уравнения первого порядка.
Уравнение Бернулли.
Определение. Линейным дифференциальным уравнением первого порядка называется уравнение линейное относительно неизвестной функции и ее производной.
Линейное уравнение имеет вид y ’ + p (x)· y = q (x), 15)
где p(x) и q(x) в дальнейшем будем считать непрерывными функциями в той области, в которой требуется проинтегрировать уравнение (15).
Если q (x) = 0, то уравнение
y ’ + p (x)· y = 0 (16)
называется однородным и решением будет функция
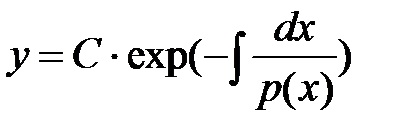 ,C ≠ 0. (17)
,C ≠ 0. (17)
Для интегрирования неоднородного уравнения (15) может быть применен метод вариации произвольной постоянной.
Он заключается в следующем: 1. Находим решение (17) однородного уравнения (16); 2. В решении (17) полагаем произвольную постоянную функцией, так что
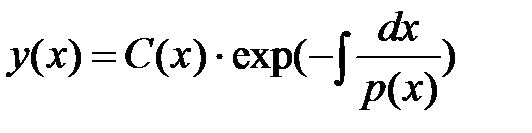 ;
;
3. находим производную этой функции как произведения
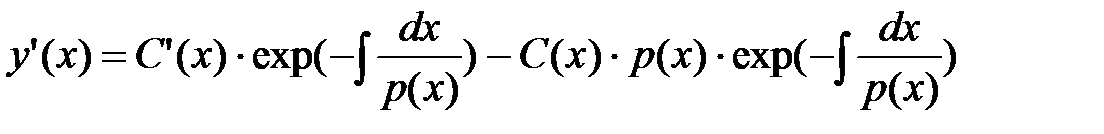 ;
;
4. подставляем функцию y(x) и ее производную y’(x) в уравнение (15) и после соответствующих преобразований получаем дифференциальное уравнение с разделяющимися переменными относительно произвольной постоянной C(x);
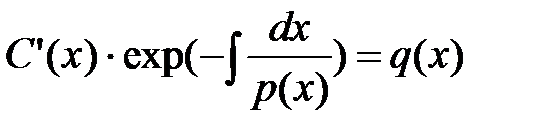
5. интегрируя дифференциальное уравнение, получаем выражение произвольной постоянной 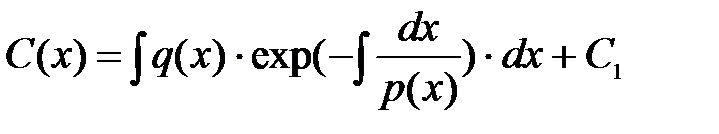 ;
;
6. подставляем произвольную постоянную в решение однородного дифференциального уравнения и получаем решение линейного дифференциального уравнения (15):
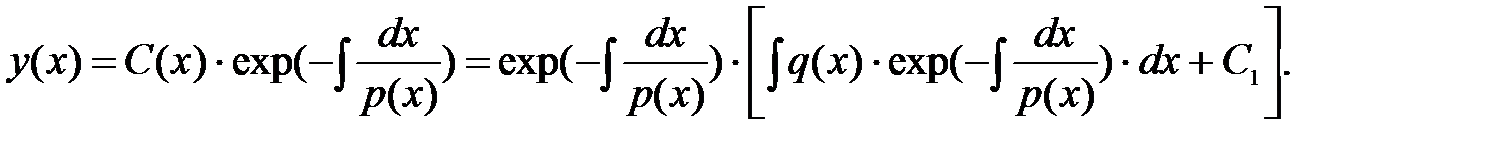 (18)
(18)
Замечание 4. Выше введено обозначение ez = exp(z).
Замечание 5. Решая линейное дифференциальное уравнение, не следует запоминать формулу (18), а рекомендуется запомнить алгоритм отыскания решения, который будет применен в других разделах.
Пример 4.1.Решить уравнение 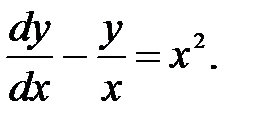
Решаем соответствующее однородное уравнение 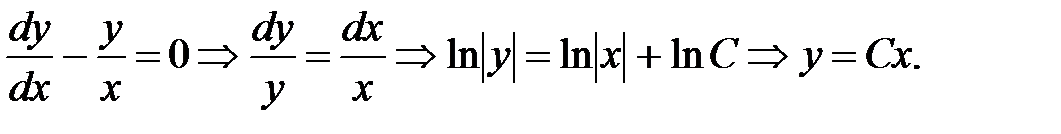 В решении полагаем постоянную C функцией C(x) и, дифференцируя это решение y’ = C’(x)·x + C, после подстановки в исходное дифференциальное уравнение получаем дифференциальное уравнение относительно C(x):x·C’(x) = x2
В решении полагаем постоянную C функцией C(x) и, дифференцируя это решение y’ = C’(x)·x + C, после подстановки в исходное дифференциальное уравнение получаем дифференциальное уравнение относительно C(x):x·C’(x) = x2 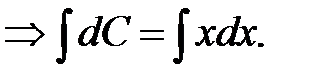 Интегрируя, получим C(x)=(x2/2) + C1. Заменяя произвольную постоянную в решении однородного уравнения, получим решение линейного уравнения: y = x(
Интегрируя, получим C(x)=(x2/2) + C1. Заменяя произвольную постоянную в решении однородного уравнения, получим решение линейного уравнения: y = x(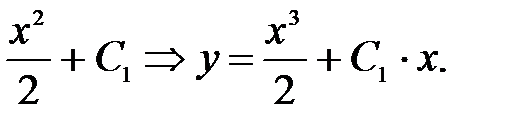
Пример 4.2. y’- y·ctgx = 2xSinx → y’- y·ctgx = 0 → 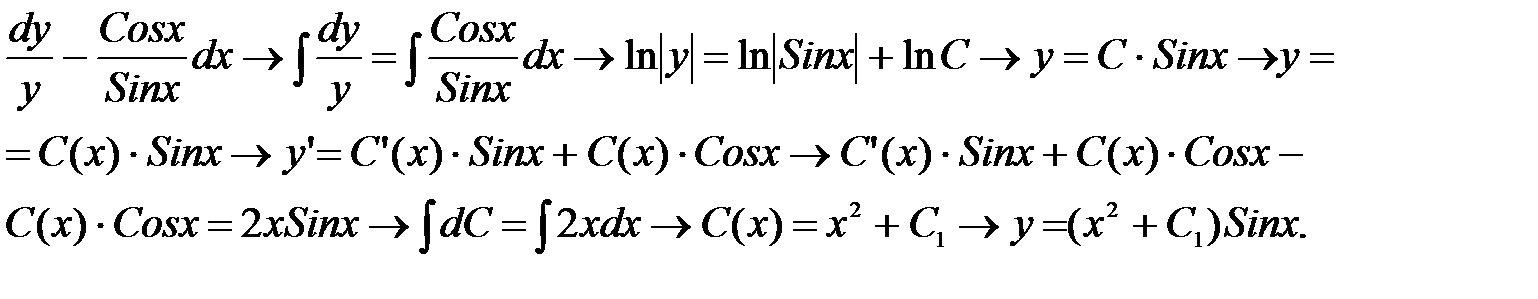
Уравнение Бернулли.
Определение. Уравнение вида y ’ + p (x)· y = yn · q (x) называется уравнением Бернулли.
Уравнение Бернулли решается также как и линейное, так как уравнение Бернулли сводится к линейному заменой z = y-(n-1). Действительно, дифференцируя замену 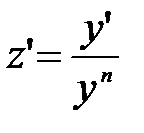 и подставляя ее вместе с производной в преобразованное уравнение Бернулли
и подставляя ее вместе с производной в преобразованное уравнение Бернулли 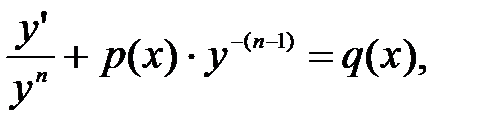 , получим линейное уравнение относительно функции z(x): z ’ + p (x)· z = q (x).
, получим линейное уравнение относительно функции z(x): z ’ + p (x)· z = q (x).
Замечание. Решая уравнение Бернулли, необязательно приводить его к линейному.
Пример 4.3. Найти решение дифференциального уравнения  . Нетрудно видеть, что это уравнение Бернулли. Решаем его методом вариации постоянной как линейное:
. Нетрудно видеть, что это уравнение Бернулли. Решаем его методом вариации постоянной как линейное: 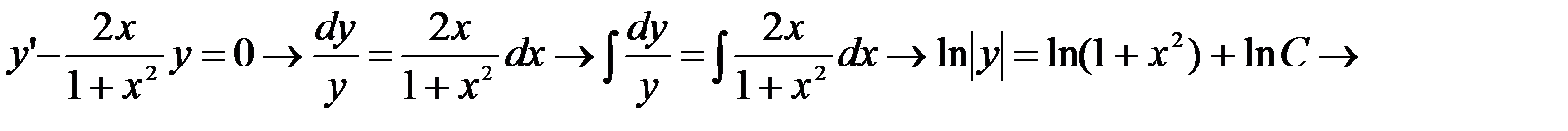 =
= 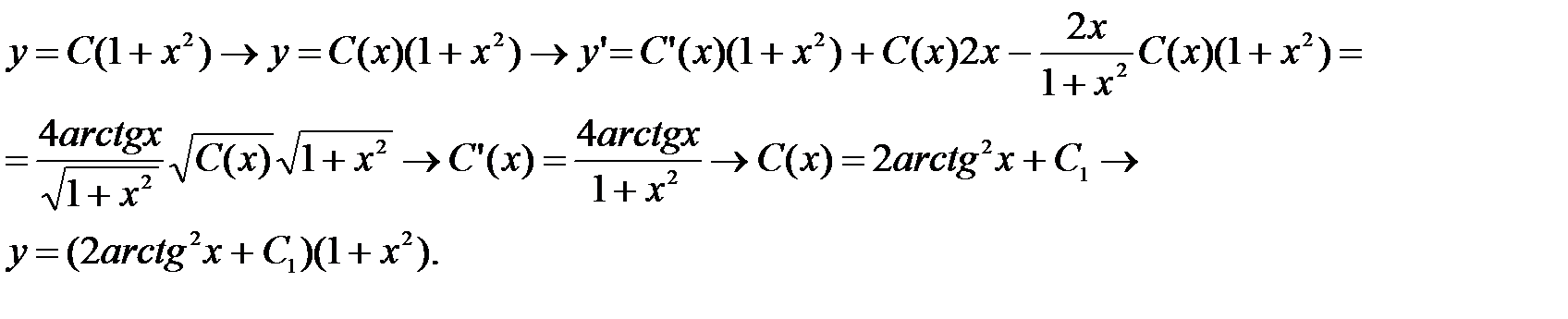
§5. Дифференциальные уравнения в полных дифференциалах



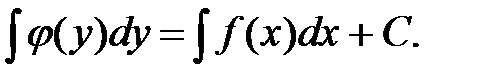
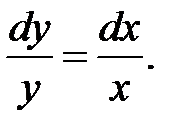 Так как уравнение с разделенными переменными, то интегрируя
Так как уравнение с разделенными переменными, то интегрируя 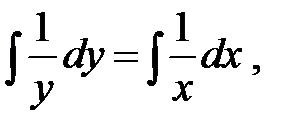 получим
получим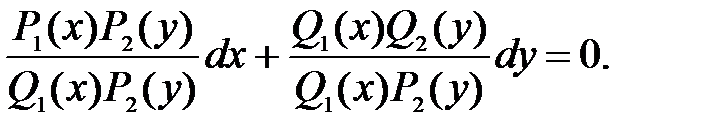
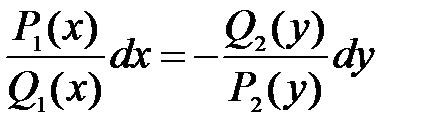 .
.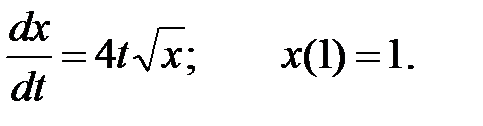
 , приведем его к уравнению с разделенными переменными:
, приведем его к уравнению с разделенными переменными: 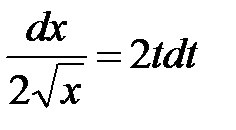 и после интегрирования получим общее решение
и после интегрирования получим общее решение 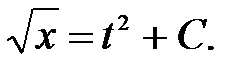 Удовлетворяя начальным условиям, т.е. подставляя в решение t=1, x=1, найдем значение произвольной постоянной: 1 =1 + С, С = 0.
Удовлетворяя начальным условиям, т.е. подставляя в решение t=1, x=1, найдем значение произвольной постоянной: 1 =1 + С, С = 0.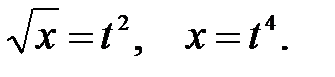
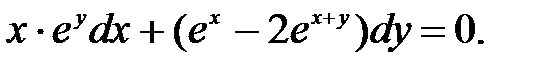
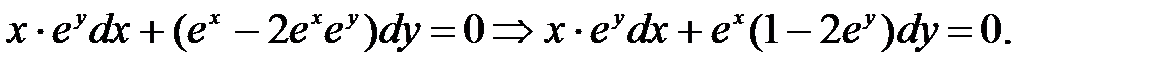 Полученное уравнение подпадает под определение дифференциального уравнения с разделяющимися переменными. Разделяя переменные,получим
Полученное уравнение подпадает под определение дифференциального уравнения с разделяющимися переменными. Разделяя переменные,получим 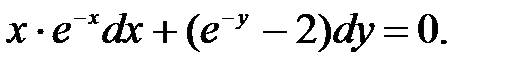 Первое слагаемое интегрируем по частям, принимая u = x, dv = e-x. В результате получим решение e-x(1+x) = e-y+2y+C.
Первое слагаемое интегрируем по частям, принимая u = x, dv = e-x. В результате получим решение e-x(1+x) = e-y+2y+C.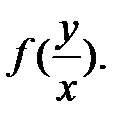 (12)
(12)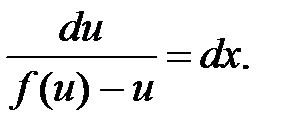
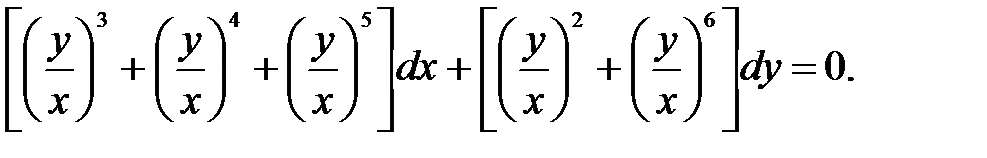
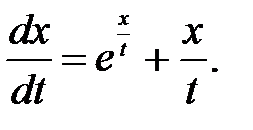 Найдем решение этого уравнения, произведя замену x = t·u,
Найдем решение этого уравнения, произведя замену x = t·u, 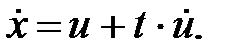 Полученное после преобразований уравнение
Полученное после преобразований уравнение 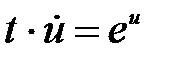 - уравнение с разделяющимися переменными. Разделяя переменные
- уравнение с разделяющимися переменными. Разделяя переменные 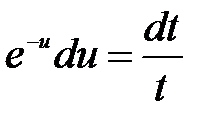 и интегрируя, получим общее решение
и интегрируя, получим общее решение 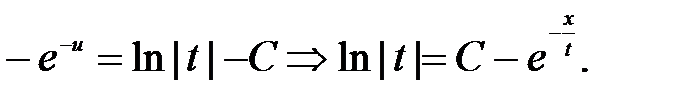
 приводится к однородному заменойX = x-x1 и Y = y-y1,гдеx1, y1- решение системы уравнений
приводится к однородному заменойX = x-x1 и Y = y-y1,гдеx1, y1- решение системы уравнений  В результате подстановки дифференциальное уравнение принимает вид
В результате подстановки дифференциальное уравнение принимает вид 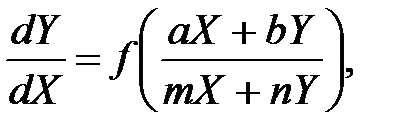 правая часть которого является однородной функцией нулевого порядка.
правая часть которого является однородной функцией нулевого порядка.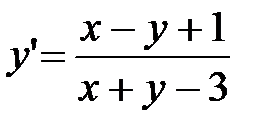 . Найдем точку пересечения двух прямых x-y+1=0 и x+y-3=0.Координаы точки пересечения будут x1=1, y=2. Полагая X=x-1, Y=y-2 и подставляя в дифференциальное уравнение, получим
. Найдем точку пересечения двух прямых x-y+1=0 и x+y-3=0.Координаы точки пересечения будут x1=1, y=2. Полагая X=x-1, Y=y-2 и подставляя в дифференциальное уравнение, получим  Произведя замену Y = uX, Y’ = u +u’X, получим
Произведя замену Y = uX, Y’ = u +u’X, получим  или, разделяя переменные -
или, разделяя переменные - 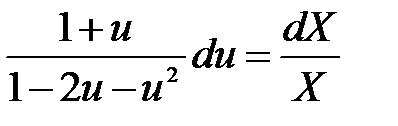 или
или 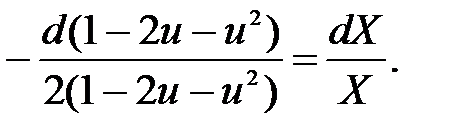 В результате интегрирования получаем общее решение C = X(1-2u-u2) или
В результате интегрирования получаем общее решение C = X(1-2u-u2) или 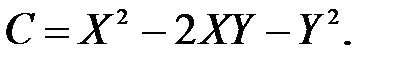 Произведя вторую обратную замену и проведя необходимые преобразования, получим окончательное общее решение x2-2xy-y2+2x+6y = C1.
Произведя вторую обратную замену и проведя необходимые преобразования, получим окончательное общее решение x2-2xy-y2+2x+6y = C1.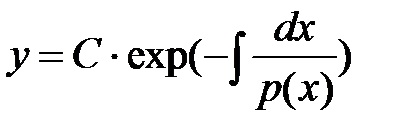 ,C ≠ 0. (17)
,C ≠ 0. (17)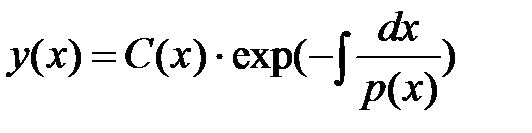 ;
;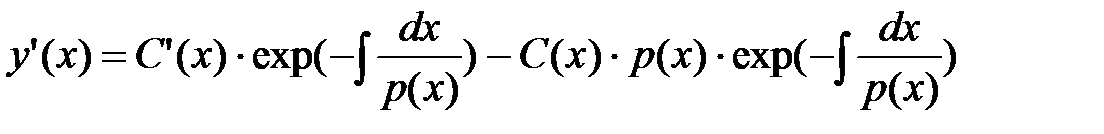 ;
; 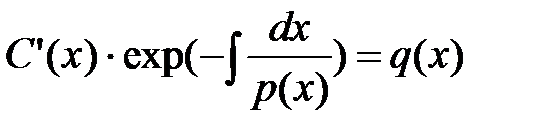
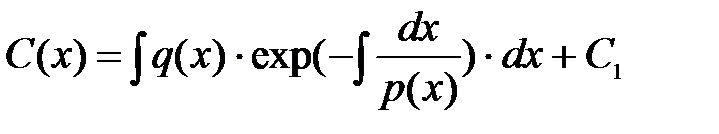 ;
;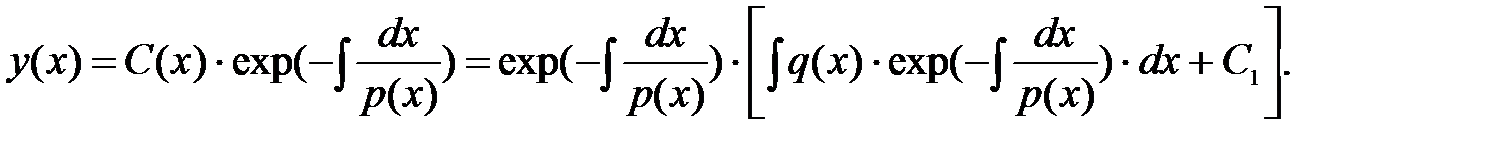 (18)
(18)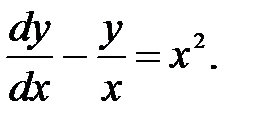
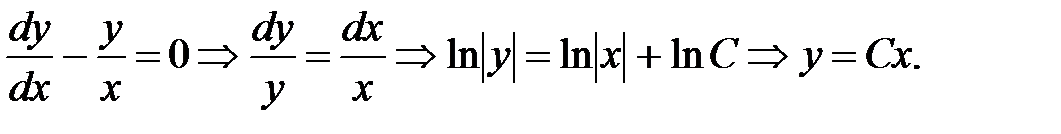 В решении полагаем постоянную C функцией C(x) и, дифференцируя это решение y’ = C’(x)·x + C, после подстановки в исходное дифференциальное уравнение получаем дифференциальное уравнение относительно C(x):x·C’(x) = x2
В решении полагаем постоянную C функцией C(x) и, дифференцируя это решение y’ = C’(x)·x + C, после подстановки в исходное дифференциальное уравнение получаем дифференциальное уравнение относительно C(x):x·C’(x) = x2 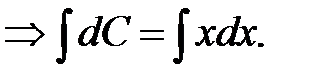 Интегрируя, получим C(x)=(x2/2) + C1. Заменяя произвольную постоянную в решении однородного уравнения, получим решение линейного уравнения: y = x(
Интегрируя, получим C(x)=(x2/2) + C1. Заменяя произвольную постоянную в решении однородного уравнения, получим решение линейного уравнения: y = x(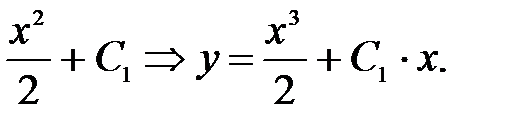
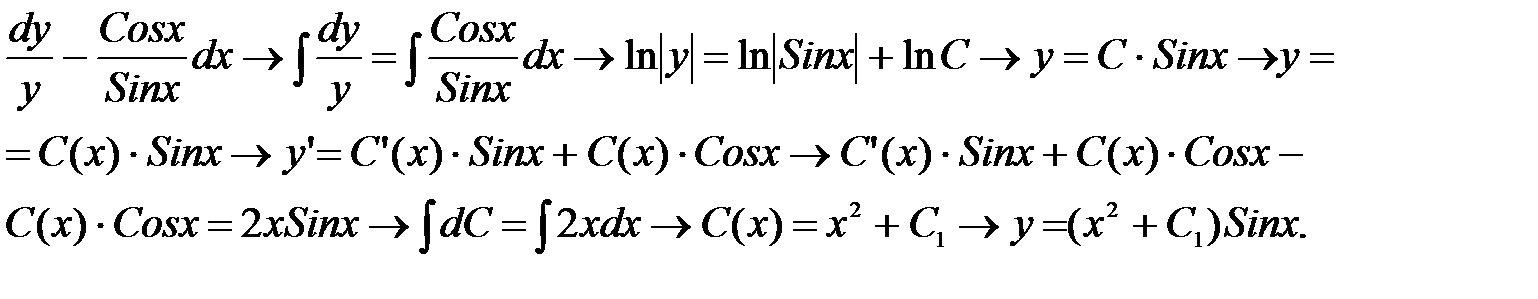
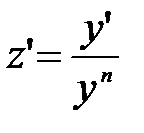 и подставляя ее вместе с производной в преобразованное уравнение Бернулли
и подставляя ее вместе с производной в преобразованное уравнение Бернулли 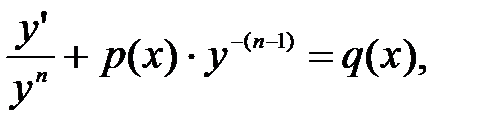 , получим линейное уравнение относительно функции z(x): z ’ + p (x)· z = q (x).
, получим линейное уравнение относительно функции z(x): z ’ + p (x)· z = q (x). . Нетрудно видеть, что это уравнение Бернулли. Решаем его методом вариации постоянной как линейное:
. Нетрудно видеть, что это уравнение Бернулли. Решаем его методом вариации постоянной как линейное: 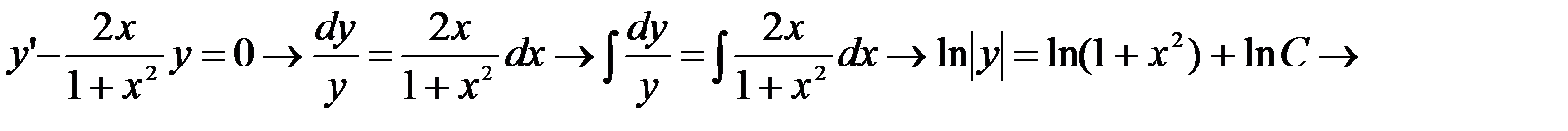 =
=