Существование гладких детерминированных решений уравнений гидродинамики, хорошо подтверждаемых как лабораторным, так и натурным экспериментами, свидетельствует о том, что турбулентные режимы течения происходят в результате некоторой трансформации исходных ламинарных течений. Исходной гипотезой при изучении этой трансформации явилось предположение о том, что переход от ламинарного течения к турбулентному происходит в результате развития некоторых возмущений, имеющих место в течениях. В соответствии с этой гипотезой и ставится задача. Итак, рассмотрим некоторое стационарное течение, задаваемое полями скорости, плотности и энергии
 (19.1)
(19.1)
и будем считать, что поля (19.1) удовлетворяют уравнениям гидродинамики. Пусть далее на исходное течение наложено некоторое зависящее от времени возмущение
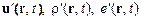 . (19.2)
. (19.2)
Рассмотрим теперь задачу Коши для возмущенного движения (19.1), (19.2). Если полученное в результате решение стремится при 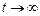 к стационарному (19.1), то исходное течение является устойчивым, в противном случае – неустойчивым. При этом наличие неустойчивости еще не означает, что результирующее течение окажется турбулентным. На самом деле эволюция течения может оказаться достаточно сложной, исходное ламинарное течение может замениться другим стационарным ламинарным течением. Таких промежуточных ламинарных течений может быть несколько. И только конечным этапом развития неустойчивости будет турбулентное течение.
к стационарному (19.1), то исходное течение является устойчивым, в противном случае – неустойчивым. При этом наличие неустойчивости еще не означает, что результирующее течение окажется турбулентным. На самом деле эволюция течения может оказаться достаточно сложной, исходное ламинарное течение может замениться другим стационарным ламинарным течением. Таких промежуточных ламинарных течений может быть несколько. И только конечным этапом развития неустойчивости будет турбулентное течение.
В случае, если возмущения бесконечно малые (или просто малые), т. е.

 ,
,  , (19.3)
, (19.3)
то говорят об устойчивости (неустойчивости) относительно малых возмущений. Если же возмущения не малы в смысле (19.3), то мы имеем задачу на устойчивость относительно конечных возмущений. На практике малыми можно считать возмущения порядка10
-5…10
-4, а возмущения порядка 5·10
-3 и выше являются конечными возмущениями. Могут реализоваться ситуации, когда исходное течение устойчиво относительно бесконечно малых возмущений, но не устойчиво относительно возмущений конечной амплитуды. Физически такое положение хорошо иллюстрируется рис. 19.1, где показан шарик, находящийся в поле тяжести на «горбатой» горке. Положение равновесия соответствует координате
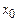
. Если возмущения достаточно малы, то шарик останется в положении равновесия в яме. При конечных же возмущениях он скатится с горки. Причем в зависимости от величины возмущения (и от направления импульса) он может скатываться либо по правому, либо по левому склону.
Рис. 19.1. Устойчивое и неустойчивые положения равновесия
тяжелого шарика на «горбатой» горке
Чтобы решить задачу гидродинамической устойчивости, необходимо еще вывести уравнения для возмущений (19.2). Если возмущения достаточно большие, то соответствующие уравнения будут нелинейными и чрезвычайно сложными, еще сложнее, чем, например, исходные уравнения Навье – Стокса. Поэтому на практике сначала рассматривают гидродинамическую задачу устойчивости относительно малых возмущений. В этом случае уравнения переноса для возмущений получаются линеаризацией исходных уравнений гидродинамики, а затем уже методом возмущений того же типа, что мы использовали при изучении нелинейного осциллятора, исследуется нелинейная задача. Такой метод оказывается применимым, поскольку не существует задач, которые были бы неустойчивы в линейном приближении, но становились бы устойчивыми относительно больших возмущений. Вот обратная ситуация, как мы видели, осуществима!
Линейная устойчивость
Плоскопараллельных течений
Для простоты здесь и ниже мы будем анализировать задачу гидродинамической устойчивости лишь для несжимаемой жидкости. Такое приближение хорошо описывает динамику жидкости, но годится также и для газа, если только скорости течения малы по сравнению со скоростью звука.
Итак, будем предполагать, что жидкость несжимаемая и описывается уравнениями Навье – Стокса (см. уравнения (12.5), (12.9), (12.11))
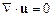 ,
, 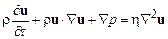 . (19.4)
. (19.4)
Для дальнейшего удобно перейти к безразмерным переменным
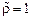 ,
, 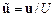 ,
, 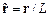 ,
,  ,
,  .
.
Здесь  – характерная скорость течения, а
– характерная скорость течения, а 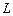 – его масштаб. В этих переменных уравнения (19.4) принимают вид (здесь и в дальнейшем тильда опущена)
– его масштаб. В этих переменных уравнения (19.4) принимают вид (здесь и в дальнейшем тильда опущена)
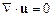 ,
,  , (19.5)
, (19.5)
где мы ввели параметр подобия течения, число Рейнольдса,
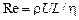 . (19.6)
. (19.6)
Уравнения для малых возмущений (19.2) получаются линеаризацией уравнений (19.5) около стационарного профиля 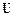 :
:
 ,
, 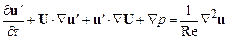 . (19.7)
. (19.7)
Эти уравнения особенно упрощаются для так называемых плоскопараллельных течений, когда профиль скорости является функцией лишь нормальной к направлению течения координаты  .
.
Уравнения (19.7) вместе с граничными и начальными условиями позволяют определить эволюцию любого малого (линейного) возмущения. В результате решения задачи можно найти профили всех возмущений и выяснить, как они ведут себя во времени. Однако на практике обычно поступают проще. Если нас интересует лишь ответ на вопрос устойчивым или нет является некоторое малое возмущение, то задачу интегрирования уравнений (19.7) можно свести к задаче на собственные значения соответствующего оператора. Поскольку коэффициенты системы (19.7) не зависят от переменных 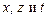 , z и t, зависимость ее решений от этих переменных должна быть экспоненциальной, что позволяет искать решение в виде плоской волны
, z и t, зависимость ее решений от этих переменных должна быть экспоненциальной, что позволяет искать решение в виде плоской волны

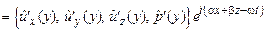 . (19.8)
. (19.8)
Подстановка решения (19.8) в уравнения (19.7) дает замкнутую систему четырех уравнений, которая вместе с необходимыми граничными условиями приводит к спектральной задаче. Для ее решения при заданных параметрах стационарного течения необходимо для каждого волнового числа  определить набор собственных частот
определить набор собственных частот  и соответствующих им собственных функций
и соответствующих им собственных функций 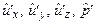 . В общем случае
. В общем случае  – комплексное число:
– комплексное число: 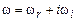 . Действительная часть
. Действительная часть 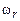 задает собственно частоту возмущения, а мнимая
задает собственно частоту возмущения, а мнимая  определяет скорость его нарастания
определяет скорость его нарастания  или затухания
или затухания  . В том случае, когда
. В том случае, когда 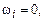 возмущение нейтрально устойчивое.
возмущение нейтрально устойчивое.
Для рассматриваемого класса течений оказывается справедливой так называемая теорема Сквайра.
Теорема Сквайра. Скорость нарастания возмущений, направленных под углом к оси течения (трехмерных по отношению к течению), та же, что и для возмущений, распространяющихся вдоль оси (двумерных) при меньшем числе Рейнольдса.
В результате для определения характера устойчивости течения на линейной стадии достаточно, как правило, изучить эволюцию двумерных возмущений. В частности, важнейшей характеристикой устойчивости течения являются кривые нейтральной устойчивости, определяющие зависимость волновых чисел нейтрально устойчивых возмущений от числа Рейнольдса. Эти кривые, таким образом, разделяют область устойчивых и неустойчивых параметров течения. Для плоского течения Пуазейля (течение в плоском канале, ограниченном двумя твердыми плоскостями
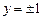
) со стационарным профилем скорости
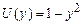
кривая нейтральной устойчивости представлена на рис. 19.2. Значение числа Рейнольдса вблизи «носика» кривой нейтральной устойчивости называют числом Рейнольдса перехода.
Рис. 19.2. Кривая нейтральной устойчивости
плоского течения Пуазейля



 (19.1)
(19.1)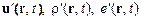 . (19.2)
. (19.2)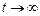 к стационарному (19.1), то исходное течение является устойчивым, в противном случае – неустойчивым. При этом наличие неустойчивости еще не означает, что результирующее течение окажется турбулентным. На самом деле эволюция течения может оказаться достаточно сложной, исходное ламинарное течение может замениться другим стационарным ламинарным течением. Таких промежуточных ламинарных течений может быть несколько. И только конечным этапом развития неустойчивости будет турбулентное течение.
к стационарному (19.1), то исходное течение является устойчивым, в противном случае – неустойчивым. При этом наличие неустойчивости еще не означает, что результирующее течение окажется турбулентным. На самом деле эволюция течения может оказаться достаточно сложной, исходное ламинарное течение может замениться другим стационарным ламинарным течением. Таких промежуточных ламинарных течений может быть несколько. И только конечным этапом развития неустойчивости будет турбулентное течение.
 ,
,  , (19.3)
, (19.3)
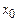 . Если возмущения достаточно малы, то шарик останется в положении равновесия в яме. При конечных же возмущениях он скатится с горки. Причем в зависимости от величины возмущения (и от направления импульса) он может скатываться либо по правому, либо по левому склону.
. Если возмущения достаточно малы, то шарик останется в положении равновесия в яме. При конечных же возмущениях он скатится с горки. Причем в зависимости от величины возмущения (и от направления импульса) он может скатываться либо по правому, либо по левому склону.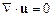 ,
, 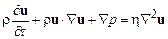 . (19.4)
. (19.4)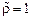 ,
, 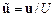 ,
, 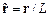 ,
,  ,
,  .
. – характерная скорость течения, а
– характерная скорость течения, а 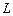 – его масштаб. В этих переменных уравнения (19.4) принимают вид (здесь и в дальнейшем тильда опущена)
– его масштаб. В этих переменных уравнения (19.4) принимают вид (здесь и в дальнейшем тильда опущена) , (19.5)
, (19.5)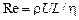 . (19.6)
. (19.6)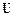 :
: ,
, 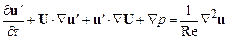 . (19.7)
. (19.7) .
.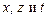 , z и t, зависимость ее решений от этих переменных должна быть экспоненциальной, что позволяет искать решение в виде плоской волны
, z и t, зависимость ее решений от этих переменных должна быть экспоненциальной, что позволяет искать решение в виде плоской волны
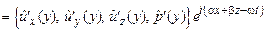 . (19.8)
. (19.8) определить набор собственных частот
определить набор собственных частот  и соответствующих им собственных функций
и соответствующих им собственных функций 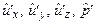 . В общем случае
. В общем случае 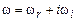 . Действительная часть
. Действительная часть 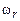 задает собственно частоту возмущения, а мнимая
задает собственно частоту возмущения, а мнимая  определяет скорость его нарастания
определяет скорость его нарастания  или затухания
или затухания  . В том случае, когда
. В том случае, когда 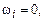 возмущение нейтрально устойчивое.
возмущение нейтрально устойчивое.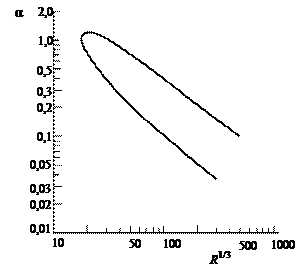
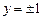 ) со стационарным профилем скорости
) со стационарным профилем скорости 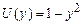 кривая нейтральной устойчивости представлена на рис. 19.2. Значение числа Рейнольдса вблизи «носика» кривой нейтральной устойчивости называют числом Рейнольдса перехода.
кривая нейтральной устойчивости представлена на рис. 19.2. Значение числа Рейнольдса вблизи «носика» кривой нейтральной устойчивости называют числом Рейнольдса перехода.



