Жидкости определяется балансом
Между ее сжимаемостью и инерцией.
Джеймс Лайтхилл
Нелинейные волны с дисперсией
Волновые движения являются типичными для самых разных сред. В газах – это звуковые волны, ударные волны, в жидкос-
тях – волновые движения в реках, морях и океанах, в каналах и трубопроводах. Волновые движения в плазме, электромагнитные волны, альвеновские и магнитозвуковые волны. А если вспомнить, что волновые свойства демонстрируют электрон и другие элементарные частицы, то становится ясно, что волновые движения – одни из самых типичных в природе. В этом разделе мы рассмотрим некоторые характерные модели волновых движений в сплошной среде, обращая основное внимание на нелинейные и дисперсионные эффекты. Дисперсионными называются волновые процессы, в которых скорость волны изменяется в зависимости от ее длины.
Гравитационные волны на поверхности жидкости
Гравитационные волны, возникающие под действием силы тяжести на поверхности воды, являются типичным примером волновых движений, возникающих в сплошной среде. Будем считать жидкость идеальной и несжимаемой. Последнее означает, что плотность жидкости не меняется под влиянием изменения давления и уравнение неразрывности сводится к такому:
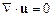 . (14.1)
. (14.1)
Пусть далее движение жидкости потенциальное
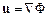 . (14.2)
. (14.2)
Выберем систему координат так, чтобы ось 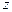 была направлена вертикально вверх, а плоскость
была направлена вертикально вверх, а плоскость  совпадала с поверхностью невозмущенной жидкости. Движение среды описывается уравнением Эйлера
совпадала с поверхностью невозмущенной жидкости. Движение среды описывается уравнением Эйлера
 .
.
Здесь учтено, что сила тяжести также потенциальна. Подставляя в последнее уравнение выражение (14.2), интегрируя его и учитывая, что внешнее давление на свободную поверхность жидкости постоянно и равно  (атмосферное давление), получим
(атмосферное давление), получим
 . (14.3)
. (14.3)
С другой стороны, уравнение неразрывности (14.1) с услови-ем (14.2) дает
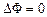 . (14.4)
. (14.4)
Таким образом, задача сводится к решению системы уравнений (14.3), (14.4) с соответствующими граничными условиями на свободной поверхности и на дне. Первое условие называется кинематическим и следует из простого факта: производные по времени от координат точек поверхности жидкости должны равняться скоростям этих точек. Представляя уравнение поверхности в виде
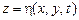 (14.5)
(14.5)
и дифференцируя его, находим
 . (14.6)
. (14.6)
Необходимо, однако, еще одно условие. Оно называется динамическим, поскольку следует непосредственно из уравнения (14.3)
 . (14.7)
. (14.7)
Последнее условие – это условие непротекания
 . (14.8)
. (14.8)
Здесь 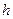 – глубина жидкости.
– глубина жидкости.
В линейном приближении, т. е. для волн малой амплитуды, когда 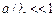 , где
, где 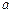 – амплитуда волны, а
– амплитуда волны, а 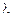 – ее длина, эти соотношения существенно упрощаются и задача сводится к системе уравнений
– ее длина, эти соотношения существенно упрощаются и задача сводится к системе уравнений
 ,
, 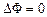 (14.9)
(14.9)
С граничными условиями
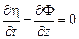 ,
,  (14.10)
(14.10)
или
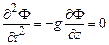 при
при  . (14.10а)
. (14.10а)
Решениями уравнений (14.9) в области 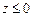 , удовлетворяющими граничному условию (14.10а), будут поверхностные гравитационные волны. Естественно, должно удовлетворяться и условие непротекания (14.8). Если глубина водоема много больше длины волны, то это условие выполняется автоматически, возмущение не проникает на глубину, существенно большую
, удовлетворяющими граничному условию (14.10а), будут поверхностные гравитационные волны. Естественно, должно удовлетворяться и условие непротекания (14.8). Если глубина водоема много больше длины волны, то это условие выполняется автоматически, возмущение не проникает на глубину, существенно большую 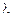 . Возникающие при этом волны называются волнами на глубокой воде. Потенциал скорости, описывающий распространение синусоидальной волны в положительном направлении оси
. Возникающие при этом волны называются волнами на глубокой воде. Потенциал скорости, описывающий распространение синусоидальной волны в положительном направлении оси  со скоростью
со скоростью  имеет вид
имеет вид
 (14.11)
(14.11)
Здесь волновое число так связано с длиной волны: 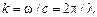 . Далее можно показать, что амплитуда волны определяется выражением
. Далее можно показать, что амплитуда волны определяется выражением
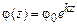 (14.12)
(14.12)
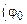 – значение при
– значение при 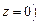 . Из граничного условия (14.10а) тогда получаем следующее дисперсионное соотношение (т. е. соотношение между частотой и длиной волны или волновым вектором) для волн на глубокой воде:
. Из граничного условия (14.10а) тогда получаем следующее дисперсионное соотношение (т. е. соотношение между частотой и длиной волны или волновым вектором) для волн на глубокой воде:
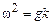 или
или 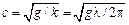 . (14.13)
. (14.13)
Таким образом, для рассматриваемых волн скорость волны пропорциональна корню квадратному из длины волны.
Для синусоидальных волн на воде произвольной, но постоянной глубины дисперсионное соотношение становится существенно более сложным
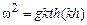 . (14.14)
. (14.14)
При 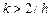 отсюда получается дисперсионное соотноше-
отсюда получается дисперсионное соотноше-
ние (14.13).



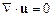 . (14.1)
. (14.1)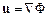 . (14.2)
. (14.2)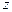 была направлена вертикально вверх, а плоскость
была направлена вертикально вверх, а плоскость  совпадала с поверхностью невозмущенной жидкости. Движение среды описывается уравнением Эйлера
совпадала с поверхностью невозмущенной жидкости. Движение среды описывается уравнением Эйлера .
. (атмосферное давление), получим
(атмосферное давление), получим . (14.3)
. (14.3)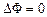 . (14.4)
. (14.4)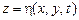 (14.5)
(14.5) . (14.6)
. (14.6) . (14.7)
. (14.7) . (14.8)
. (14.8)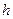 – глубина жидкости.
– глубина жидкости.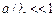 , где
, где 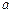 – амплитуда волны, а
– амплитуда волны, а 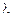 – ее длина, эти соотношения существенно упрощаются и задача сводится к системе уравнений
– ее длина, эти соотношения существенно упрощаются и задача сводится к системе уравнений ,
, 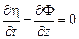 ,
,  (14.10)
(14.10)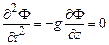 при
при  . (14.10а)
. (14.10а)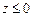 , удовлетворяющими граничному условию (14.10а), будут поверхностные гравитационные волны. Естественно, должно удовлетворяться и условие непротекания (14.8). Если глубина водоема много больше длины волны, то это условие выполняется автоматически, возмущение не проникает на глубину, существенно большую
, удовлетворяющими граничному условию (14.10а), будут поверхностные гравитационные волны. Естественно, должно удовлетворяться и условие непротекания (14.8). Если глубина водоема много больше длины волны, то это условие выполняется автоматически, возмущение не проникает на глубину, существенно большую  со скоростью
со скоростью  имеет вид
имеет вид (14.11)
(14.11)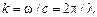 . Далее можно показать, что амплитуда волны определяется выражением
. Далее можно показать, что амплитуда волны определяется выражением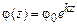 (14.12)
(14.12)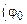 – значение при
– значение при 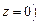 . Из граничного условия (14.10а) тогда получаем следующее дисперсионное соотношение (т. е. соотношение между частотой и длиной волны или волновым вектором) для волн на глубокой воде:
. Из граничного условия (14.10а) тогда получаем следующее дисперсионное соотношение (т. е. соотношение между частотой и длиной волны или волновым вектором) для волн на глубокой воде: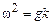 или
или 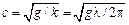 . (14.13)
. (14.13)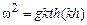 . (14.14)
. (14.14)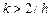 отсюда получается дисперсионное соотноше-
отсюда получается дисперсионное соотноше-


