Экспонента и число е: просто и понятно

Экспонента и число е: просто и понятно

1. Главная

Перевод большой статьи "An Intuitive Guide To Exponential Functions & e"

Число e всегда волновало меня — не как буква, а как математическая константа. Что число е означает на самом деле?

Разные математические книги и даже моя горячо любимая Википедия описывает эту величественную константу совершенно бестолковым научным жаргоном:

Математическая константа е является основанием натурального логарифма.

Если заинтересуетесь, что такое натуральный логарифм, найдете такое определение:

Натуральный логарифм, ранее известный как гиперболический логарифм, является логарифмом с основанием е, где е – иррациональная константа, приблизительно равная 2.718281828459.

Определения, конечно, правильные. Но понять их крайне сложно. Конечно, Википедия в этом не виновата: обычно математические пояснения сухи и формальны, составляются по всей строгости науки. Из-за этого новичкам сложно осваивать предмет (а когда-то каждый был новичком).

С меня хватит! Сегодня я делюсь своими высокоинтеллектуальными соображениями о том, что такое число е, и чем оно так круто! Отложите свои толстые, наводящие страх математические книжки в сторону!

Число е – это не просто число

Описывать е как «константу, приблизительно равную 2,71828…» — это все равно, что называть число пи «иррациональным числом, приблизительно равным 3,1415…». Несомненно, так и есть, но суть по-прежнему ускользает от нас.

Число пи — это соотношение длины окружности к диаметру, одинаковое для всех окружностей. Это фундаментальная пропорция, свойственная всем окружностям, а следовательно, она участвует в вычислении длины окружности, площади, объема и площади поверхности для кругов, сфер, цилиндров и т.д. Пи показывает, что все окружности связаны, не говоря уже о тригонометрических функциях, выводимых из окружностей (синус, косинус, тангенс).

Число е является базовым соотношением роста для всех непрерывно растущих процессов. Число е позволяет взять простой темп прироста (где разница видна только в конце года) и вычислить составляющие этого показателя, нормальный рост, при котором с каждой наносекундой (или даже быстрее) всё вырастает еще на немного.

Число е участвует как в системах с экспоненциальным, так и постоянным ростом: население, радиоактивный распад, подсчет процентов, и много-много других. Даже ступенчатые системы, которые не растут равномерно, можно аппроксимировать с помощью числа е.

Также, как любое число можно рассматривать в виде «масштабированной» версии 1 (базовой единицы), любую окружность можно рассматривать в виде «масштабированной» версии единичной окружности (с радиусом 1). И любой коэффициент роста может быть рассмотрен в виде «масштабированной» версии е («единичного» коэффициента роста).

Так что число е – это не случайное, взятое наугад число. Число е воплощает в себе идею, что все непрерывно растущие системы являются масштабированными версиями одного и того же показателя.

Приглядимся поближе

Наша формула предполагает, что прирост происходит дискретными шагами. Наши бактерии ждут, ждут, а потом бац!, и в последнюю минуту они удваиваются в количестве. Наша прибыль по процентам от депозита магическим образом появляется ровно через 1 год. На основе формулы, написанной выше, прибыль растет ступенчато. Зеленые точки появляются внезапно.

Но мир не всегда таков. Если мы увеличим картинку, мы увидим, что наши друзья-бактерии делятся постоянно:

Зеленый малый не возникает из ничего: он медленно вырастает из синего родителя. После 1 периода времени (24 часа в нашем случае), зеленый друг уже полностью созрел. Повзрослев, он стает полноценным синим членом стада и может создавать новые зеленые клеточки сам.

Эта информация как-то изменит наше уравнение? Не-а. В случае с бактериями, полусформированные зеленые клетки все же не могут ничего делать, пока не вырастут и совсем не отделятся от своих синих родителей. Так что уравнение справедливо.

Экспонента и число е — деньги как пример

В прошлой статье "Экспонента и число е: просто и понятно" мы рассмотрели понятие экспоненциального роста на примере базовой системы, которая удваивается за определенный период времени.

Но деньги меняют все

С деньгами дела обстоят по-другому. Как только мы зарабатываем пару монет прибыли, эти монетки начинают приносить свои микро-прибыли. Нет необходимости ждать, пока набежит целый рубль — «свежим» денежкам совсем не нужно «дозревать», чтобы начать «плодоносить».

Основываясь на нашей старой формуле, прирост процента выглядит примерно так:

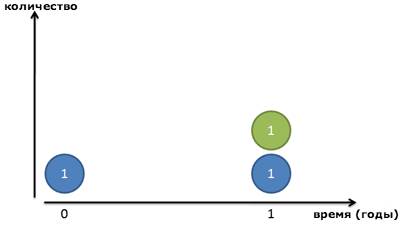
Но опять же, это не совсем правильно: вся сумма процента появляется в последний день. Давайте посмотрим поближе и разделим год на два промежутка. Мы зарабатываем 100% прибыль каждый год, или по 50% каждые 6 месяцев. Таким образом, мы заработаем 50 копеек в первые полгода, и другие 50 копеек во вторую половину года:

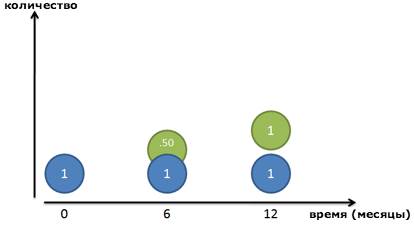
И все равно, это неверно! Конечно, наш рубль-родитель (Синий кружок) зарабатывает рубль в течение года. Но после 6 месяцев мы получим 50-копеечный кусочек прибыли – готовые деньги, которыми мы пренебрегаем! Эти 50 копеек уже могли бы зарабатывать свои собственные деньги:

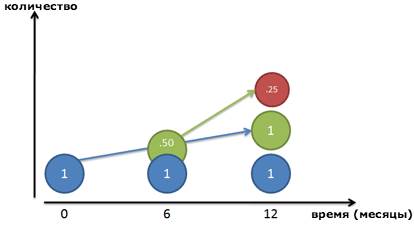
Поскольку наш коэффициент равен 50% каждые полгода, эти 50 копеек могли бы заработать еще 25 копеек (50% от 50 копеек). В конце года мы бы получили:

· Наш начальный рубль (Синий кружок)

· Рубль, который заработал Синий (Зеленый кружок)

· 25 копеек, которые заработал Зеленый (Красный кружок)

Если все сложить, получится 2,25 рублей. Мы заработали 1,25 рубля всего на одном исходном рубле, и это даже лучше, чем удвоение!

Вернемся к формуле. Рост за два полу-периода по 50% составит:

рост = (1+100%/2)² = 2,25

Переходим на составной рост

Идем дальше. Давайте поделим рост не на два периода по 50%, а на 3 сегмента по 33% каждый. Кто сказал, что надо ждать целых 6 месяцев до начала получения прибыли? Давайте детализируем наши вычисления.

Вот так выглядит наш рост, расписанный на 3 составных периода:

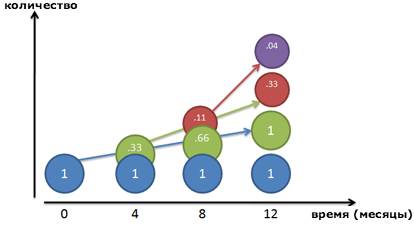
Каждый отдельный цвет обозначает определенное «поколение» прибыли. Тогда картина выглядит так:

· Месяц 0: Мы начали с 1 рубля (Синий)

· Месяц 4: Синий родитель заработал 1/3 рубля сам, то есть родил Зеленого детеныша, равного 33 копейкам.

· Месяц 8: Синий родитель заработал еще 33 копейки, его Зеленый детеныш, соответственно, на столько же подрос. За этот период Зеленый детеныш уже заработал свои 11 копеек (33% от 33 копеек). Эти 11 копеек становятся Красным внуком.

· Месяц 12: Процесс становится еще интереснее. Синий родитель зарабатывает еще 33 копейки, и его Зеленый детеныш совсем повзрослев, став целым рублем. Зеленый и сам заработал 22 копейки за последние 4 месяца, поэтому его Красный ребенок весит уже 33 копейки. И Красный, будучи в возрасте 11 копеек в начале этого промежутка, заработал свои 4 копейки (33% от 11 копеек) – и это уже его Фиолетовый детёныш.

Фуух! Спустя 12 месяцев у нас получается: 1 + 1 + 0.33 + 0.04 или примерно 2.37 рубля.

Потратим еще чуть времени, чтобы понять, что на самом деле происходит с таким ростом:

· Каждый цвет зарабатывает свой процент и «передает» его другому цвету. Заработанные деньги могут зарабатывать свои собственные прибыли, и этот цикл повторяется.

· Мне нравится думать, что начальная сумма (Синий родитель) никогда не меняется. Синий вкладывает свои заработки в рождение Зеленого, 33 копейки каждые 4 месяца, а сам не растет. На графике синими стрелками показано, как Синий родитель кормит своего Зеленого малыша.

· Зелёный родитель только что произвёл на свет красного (зелёные стрелки), но синий родитель про это не знает ни сном ни духом.

· Сам Зеленый постоянно растет (на кормежке Синего родителя), вкладывая все больше и больше в свое Красное дитя. Между 4 и 8 месяцами Зеленый отдает 11 копеек Красному. Между 8 и 12 месяцем Зеленый дает 22 копейки Красному, так как сам он к 8 месяцу вырос до 66 копеек. Если бы мы удлинили нашу диаграмму, Зеленый бы отдал Красному 33 копейки, так как сам он к 12 месяцу подрос до целого рубля.

Теперь понятнее? Поначалу это сложно — я и сам запутался, пока рисовал все эти графики. Главное понять, что каждый «рубль» создает маленьких помощников, а те, в свою очередь, создают помощников себе, и так далее.

Если рассматривать год как 3 равных периода, формула роста будет такой:

рост = (1 + 100%/3)³ = 2.37037...

Мы заработали 1.37 рубля, а это даже лучше, чем те 1.25, что получились у нас в предыдущий раз!

И что все это значит?

Число е (2.718) — это максимально возможный результат при распределении 100% роста в течение одного периода времени. Конечно, начали мы, ожидая рост с 1 до 2 (это и есть 100% увеличение, правда?). Но с каждым крошечным шажком вперед, мы получаем маленькие «дивиденды», которые начинают сами по себе расти. Когда все сказано и сделано, в конце 1 периода времени мы получили е (2.718…), а не 2. Число е — это максимум, который случается при разбиении 100% на самые мелкие промежутки.

Так, если мы начнем с 1 рубля и разложим непрерывно 100% прироста, мы получим 1е. Если в качестве начальной суммы взять 2 рубля, в итоге получим 2е. Если мы начнем с 11.79 рублей, получим 11.79е.

Число е — это нечто вроде предела скорости (как "число с" — скорость света). Эта константа показывает, как быстро можно вырасти, используя непрерывный процесс. Вы можете не всегда достигать предела скорости, но это удобная точка сравнения: вы можете описать любой коэффициент роста с помощью этой универсальной константы.

(Отступление: будьте осторожны, отличайте понятие увеличения от понятия конечного результата. 1, становящаяся е (2.718…), увеличилась (коэффициент роста) на 171.8%. Число е, само по себе, является конечным результатом, который вы видите после того, как весь прирост зачислен (начальная сумма + прирост)).

Пример 1: Наращивание кристаллов

Предположим, у меня есть 300 кг магических кристаллов. Они магические, потому что растут в течение дня: сначала я вижу один кристалл, а через 24 часа он выбрасывает из себя другой кристалл, весом как он сам. (Кристаллы-детки начинают расти сразу же, и с таким же темпом, но я это уже не могу отследить — я могу увидеть только вот эту первую партию новорожденных). Сколько кристаллов будет у меня через 10 дней?

В общем, так как кристаллы начинают расти немедленно, мы имеем дело с непрерывным ростом. Наш коэффициент прироста 100% каждые 24 часа, так что через 10 дней мы получим 300 × e^{1 × 10} = 6.6 миллионов кг магических самоцветов.

Здесь может быть загвоздка: видите, какая разница между исходным коэффициентом и общим коэффициентом прироста. «Исходный» — это насколько изменяется один кристалл: 100% за 24 часа. Общий прирост равен числу е (2.718х), потому что детки-кристаллы тоже постоянно растут.

В этом случае у нас есть исходный коэффициент (как быстро растут кристаллы), и мы хотим получить совокупный результат (как вся группа вырастет с учетом кристаллов-деток). Если у нас есть общий прирост, а вычислить требуется исходный коэффициент (рост одного кристалла за определенный период времени), мы вычисляем в обратном порядке и используем натуральный логарифм.

Пример 2: максимальная ставка процента

Допустим, у меня есть 120 рублей на счету в банке с 5% ставкой. Мой банк очень щедр, и обеспечивает мне максимально возможную капитализацию. Сколько у меня будет денег через 10 лет?

Наша ставка составляет 5%, и нам повезло с непрерывной капитализацией. После 10 лет мы получим 120 × e^{0.05 × 10} = 197,85 рублей. Конечно, большинство банков не настолько хороши, чтобы предоставить вам лучший из возможных процентов. Разница между вашей конечной суммой и размером непрерывного прироста показывает, насколько именно они жадничают..

Пример 3: радиоактивный распад

У меня 10 кг радиоактивного материала, который непрерывно распадается с коэффициентом 100% в год. Как много у меня останется через 3 года?

Совсем ничего? Ноль без палочки? Подумайте еще раз.

Распадаться непрерывно на 100% в год — примерно такую ситуацию мы рассматривали в начале. Да, мы начали с 10 кг, и ожидаем потерять все к концу первого же года, так как материал распадается на 10 кг/год.

Наше радиотопливо распадалось несколько месяцев, и осталось всего 5 кг материала. До полного распада осталось полгода? Неа! Теперь мы теряем в весе уже 5 кг/год, так что у нас еще целый год для полного распада!

Мы ждем еще несколько месяцев, и доходим до 2 кг. И конечно же, дальнейший распад уже пойдет со скоростью 2 кг/год, так что у нас еще в запасе полный год (с этого момента). Мы доходим до 1 кг, и опять в запасе целый год, так мы достигнем 0,5 кг, еще один год – улавливаете схему?

С течением времени мы теряем материал, но и скорость распада постепенно уменьшается. Этот постоянно изменяющийся темп и лежит в основе непрерывного роста и распада.

Спустя три года, у нас останется 10 × e^{-1 × 3} = 0.498 кг. Мы использовали отрицательную степень для распада – нам нужна дробь (1/e^{п × в}) вместо произведения роста (е^{п × в}). (Распад обычно дается в контексте «полураспада» — мы поговорим о преобразовании этих показателей в другой статье).

Больше примеров

Если вы хотите более сложные примеры, попробуйте формулу опционов Блэка-Шоулза (число е используется для экспоненциального снижения в цене) или радиоактивный распад. Цель таких примеров — дать человеку увидеть е^{п × в} в формуле и понять, почему она там: это и моделирует прирост или распад.

Сейчас вы знаете, почему константа называется «е», а не «пи» или другое какое-то число: е, возведенная в степень «п × в», позволяет оценить влияние коэффициента прироста П и времени В.

Еще многому предстоит научиться!

Моей целью было:

· Объяснить, почему так важна константа е: это фундаментальная константа, как «пи», которая отражается в темпах роста.

· Дать понятное, логическое объяснение: число е дает вам увидеть влияние любого коэффициента роста. Каждый новый «кусочек» (вспомните наших цветных друзей на графиках) делает свой вклад в общий прирост.

· Показать, где это используется: e^x позволяет предсказать, как повлияет определенный коэффициент роста и период времени на имеющуюся величину.

· Разжечь ваш аппетит перед следующим блюдом: в будущих статьях мы изучим другие свойства числа е.

Эта статья – только начало. Если попытаться впихнуть все в одну страничку, это утомит моих читателей, и мне самому станет скучно. Стряхните с себя пыль, отвлекитесь и узнайте много интересного о близнеце числа е — натуральным логарифмом.

 

Число e означает рост

Число e означает непрерывный рост. Как мы видели в прошлом примере, e^x позволяет нам увязать процент и время: 3 года при росте 100% есть то же самое, что и 1 год при 300%, при условии "сложных процентов".

Можно подставлять любые значения процента и времени (50% на протяжении 4 лет), но лучше задать процент как 100% для удобства (получается 100% на протяжении 2 лет). За счёт перехода к 100% мы можем сфокусироваться исключительно на компоненте времени:

e^x = e^{процент * время} = e^{1.0 * время} = e^время

Очевидно, что e^x означает:

· насколько вырастет мой вклад через x единиц времени (при условии 100%-го непрерывного роста).

· например, через 3 промежутка времени я получу в e³ = 20.08 раз больше "штуковин".

e^x — это масштабирующий коэффициент, показывающий, до какого уровня мы вырастем за x отрезков времени.

Что дальше?

Надеюсь, натуральный логарифм теперь приобрёл для вас смысл — он показывает время, необходимое для роста любого числа при экспоненциальном росте. Я думаю, натуральным он называется потому, что e — универсальная мера роста, так что ln можно считать универсальным способом определения, сколько времени нужно для роста.

Каждый раз, когда вы видите ln(x), вспоминайте "время, нужное, чтобы вырасти в Х раз". В предстоящей статье я опишу e и ln в связке, так что свежий аромат математики заполнит воздух.

Экспонента

[править | править код]

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 января 2021; проверки требует 1 правка.

Перейти к навигацииПерейти к поиску

У этого термина существуют и другие значения, см. Экспонента (значения).

Запрос «EXP» перенаправляется сюда; о классе сложности см. Класс EXPTIME.

 

График экспоненты {\displaystyle y=e^{x}} (синим).
Касательная (красным) в нуле у функции {\displaystyle e^{x}} наклонена на {\displaystyle {\frac {\pi }{4}}~(45^{\circ })} .
Рядом для примера показаны {\displaystyle y=2^{x}} (точками) и {\displaystyle y=4^{x}} (штрихами)

Экспоне́нта — показательнаяфункция {\displaystyle f(x)=\exp(x)=e^{x}} , где {\displaystyle e\approx 2{,}718} — число Эйлера.

 

Содержание

· 1Определение

· 2Свойства

· 3Комплексная экспонента

o 3.1Свойства

· 4Вариации и обобщения

o 4.1Матричная экспонента

o 4.2 h -экспонента

· 5Обратная функция

· 6См. также

· 7Примечания

· 8Литература

· 9Ссылки

Определение[править |править код]

Экспоненциальная функция может быть определена различными эквивалентными способами. Например, через ряд Тейлора:

{\displaystyle e^{x}=1+\sum _{n=1}^{\infty }{x^{n} \over n!}=1+x+{x^{2} \over 2!}+{x^{3} \over 3!}+{x^{4} \over 4!}+\cdots }

или через предел:

{\displaystyle e^{x}=\lim _{n\rightarrow \infty }\left(1+{\frac {x}{n}}\right)^{n}} .

Здесь {\displaystyle x} — любое комплексное число.

Свойства[править | править код]

· {\displaystyle (e^{x})'=e^{x}} , а в частности, экспонента — единственное решение дифференциального уравнения {\displaystyle y'=y} с начальными данными {\displaystyle y(0)=1} . Кроме того, через экспоненту выражаются общие решения однородных дифференциальных уравнений.

· Экспонента определена на всей вещественной оси. На ней экспонента всюду возрастает и строго больше нуля.

· Экспонента — выпуклая функция.

· Обратная функция к ней — натуральный логарифм {\displaystyle (\ln x)} .

· Преобразование Фурье экспоненты — обобщённая функция, а именно дельта-функция Дирака.

· Преобразование Лапласа экспоненты {\displaystyle e^{ax}} определено в области {\displaystyle \operatorname {Re} (x)<a} .

· Производная в нуле равна {\displaystyle 1} , поэтому касательная к экспоненте в этой точке проходит под углом {\displaystyle 45^{\circ },} или {\displaystyle {\frac {\pi }{4}}} .

· Основное функциональное свойство экспоненты, как и всякой показательной функции:

{\displaystyle \exp(a+b)=\exp(a)\exp(b)} .

o Непрерывная функция с таким свойством либо тождественно равна {\displaystyle 0} , либо имеет вид {\displaystyle \exp(cx)} , где {\displaystyle c} — некоторая константа.

· {\displaystyle e^{x}=\operatorname {sh} x+\operatorname {ch} x} , где {\displaystyle \operatorname {sh} } и {\displaystyle \operatorname {ch} } — гиперболические синус и косинус.

Комплексная экспонента[править | править код]

 

График экспоненты в комплексной плоскости.
Легенда

Комплексная экспонента — математическая функция, задаваемая соотношением {\displaystyle f(z)=e^{z}} , где {\displaystyle z} есть комплексное число. Комплексная экспонента определяется как аналитическое продолжение экспоненты {\displaystyle f(x)=e^{x}} вещественного переменного {\displaystyle x} :

Определим формальное выражение

{\displaystyle e^{z}=e^{x+iy}=e^{x}\cdot e^{iy}} .

Определённое таким образом выражение на вещественной оси будет совпадать с классической вещественной экспонентой. Для полной корректности построения необходимо доказать аналитичность функции {\displaystyle e^{z}} , то есть показать, что {\displaystyle e^{z}} разлагается в некоторый сходящийся к данной функции ряд. Покажем это:

{\displaystyle f(z)=e^{z}=e^{x}\cdot e^{iy}=e^{iy}\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}} .

Сходимость данного ряда легко доказывается:

{\displaystyle \left|e^{iy}\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}\right|\leq \left|\sum _{n=0}^{\infty }{\frac {x^{n}}{n!}}\right|\leq \sum _{n=0}^{\infty }\left|{\frac {x^{n}}{n!}}\right|=\sum _{n=0}^{\infty }{\dfrac {|x|^{n}}{n!}}=e^{|x|}} .

Ряд всюду сходится абсолютно, то есть вообще всюду сходится, таким образом, сумма этого ряда в каждой конкретной точке будет определять значение аналитической функции {\displaystyle f(z)=e^{z}} . Согласно теореме единственности, полученное продолжение будет единственно, следовательно, на комплексной плоскости функция {\displaystyle e^{z}} всюду определена и аналитична.

Свойства[править | править код]

· Комплексная экспонента — целая голоморфная функция на всей комплексной плоскости. Ни в одной точке она не обращается в ноль.

· {\displaystyle e^{z}} — периодическая функция с основным периодом 2πi: {\displaystyle e^{i\varphi }=e^{i(\varphi +2\pi)}} . В силу периодичности комплексная экспонента бесконечнолистна. В качестве её области однолистности можно выбрать любую горизонтальную полосу высотой {\displaystyle 2\pi } .

· {\displaystyle e^{z}} — единственная с точностью до постоянного множителя функция, производная (а соответственно, и первообразная) которой совпадает с исходной функцией.

· Алгебраически экспонента от комплексного аргумента {\displaystyle z=x+iy} может быть определена следующим образом:

{\displaystyle e^{z}=e^{x+iy}=e^{x}e^{iy}=e^{x}(\cos \,y+i\sin \,y)} (формула Эйлера).

o В частности, имеет место тождество Эйлера:

{\displaystyle e^{i\pi }+1=0.}

Вариации и обобщения[править | править код]

Аналогично экспонента определяется для элемента произвольной ассоциативной алгебры. В конкретном случае требуется также доказательство того, что указанные пределы существуют.

Матричная экспонента[править | править код]

Основная статья: Матричная экспонента

Экспоненту от квадратной матрицы (или линейного оператора) можно формально определить, подставив матрицу в соответствующий ряд:

{\displaystyle \exp A=\sum _{k=0}^{\infty }{\frac {A^{k}}{k!}}.}

Определённый таким образом ряд сходится для любого оператора {\displaystyle A} с ограниченной нормой, поскольку мажорируется рядом для экспоненты нормы {\displaystyle A\colon } {\displaystyle \exp \|A\|.} Следовательно, экспонента от матрицы {\displaystyle A\in \mathbb {R} ^{n\times n}} всегда определена и сама является матрицей.

С помощью матричной экспоненты легко задать вид решения линейного дифференциального уравнения с постоянными коэффициентами: уравнение {\displaystyle {\dot {x}}=Ax,~~~x\in \mathbb {R} ^{n}} с начальным условием {\displaystyle x(0)=x_{0}} имеет своим решением {\displaystyle x(t)=\exp(At)x_{0}.}

h -экспонента[править | править код]

Введение {\displaystyle h} -экспоненты основано на втором замечательном пределе:

{\displaystyle e_{h}(x)=(1+h)^{\frac {x}{h}}.}

При {\displaystyle h\to 0} получается обычная экспонента^[1].

Обратная функция[править | править код]

Обратная функция к экспоненциальной функции — натуральный логарифм. Обозначается {\displaystyle \ln x} :

{\displaystyle \ln x=\log _{e}x.}

См. также[править | править код]

· Показательная функция

· Список интегралов от экспоненциальных функций

Примечания[править | править код]

1. ↑ A.I. Olemskoi, S.S. Borysov, a, and I.A. Shuda. Statistical field theories deformed within different calculi

Литература[править | править код]

· Лаврентьев М. А., Шабат Б. В. Методы теории функций комплексного переменного. — Издание 5-е, исправленное. — М.: Наука, 1987. — 688 с.

· Хапланов М. Г. Теория функции комплексного переменного (краткий курс). — Издание 2-е, исправленное. — М.: Просвещение, 1965. — 209 с.

Ссылки[править | править код]

· «Экспонента и число е: просто и понятно» — перевод статьи An Intuitive Guide To Exponential Functions & e | BetterExplained (англ.)

Категории:

· Элементарные функции

· Элементарные функции комплексной переменной

 

Экспонента и число е: просто и понятно

1. Главная

Перевод большой статьи "An Intuitive Guide To Exponential Functions & e"

Число e всегда волновало меня — не как буква, а как математическая константа. Что число е означает на самом деле?

Разные математические книги и даже моя горячо любимая Википедия описывает эту величественную константу совершенно бестолковым научным жаргоном:

Математическая константа е является основанием натурального логарифма.

Если заинтересуетесь, что такое натуральный логарифм, найдете такое определение:

Натуральный логарифм, ранее известный как гиперболический логарифм, является логарифмом с основанием е, где е – иррациональная константа, приблизительно равная 2.718281828459.

Определения, конечно, правильные. Но понять их крайне сложно. Конечно, Википедия в этом не виновата: обычно математические пояснения сухи и формальны, составляются по всей строгости науки. Из-за этого новичкам сложно осваивать предмет (а когда-то каждый был новичком).

С меня хватит! Сегодня я делюсь своими высокоинтеллектуальными соображениями о том, что такое число е, и чем оно так круто! Отложите свои толстые, наводящие страх математические книжки в сторону!