ГЛАВА 7. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
§1. Некоторые сведения о матрицах
Ортогональные и унитарные матрицы
Определение. Комплексная квадратная матрица А называется унитарной, если 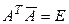 . Множество всех унитарных матриц n -го порядка будем обозначать
. Множество всех унитарных матриц n -го порядка будем обозначать  .
.
Следствия. 1. Модуль определителя унитарной матрицы равен 1.
►Из определения следует:  , значит,
, значит,  .◄
.◄
2. 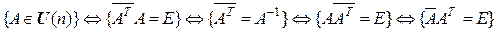 .
.
В силу равносильности любое из этих равенств может служить определением унитарной матрицы.
Определение. Действительная квадратная матрица 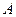 называется ортогональной, если
называется ортогональной, если 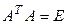 . Множество всех ортогональных матриц n -го порядка будем обозначать
. Множество всех ортогональных матриц n -го порядка будем обозначать  .
.
Следствия. 1.  .
.
2. Определитель ортогональной матрицы равен 1 или –1.
3.  .
.
Каждое из этих равенств опять же может служить определением ортогональной матрицы.
Свойства ортогональных и унитарных матриц
1º. 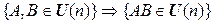 . 1'.
. 1'. 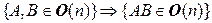 .
.
2º.  . 2'.
. 2'. 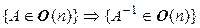 .
.
3º. 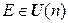 . 3'.
. 3'.  .
.
►Докажем, например, первое свойство для унитарных матриц (для ортогональных доказательство отличается только тем, что отсутствует комплексное сопряжение).
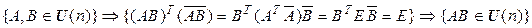 .◄
.◄
Теорема 7.1 о матрице перехода. Пусть в евклидовом пространстве  заданы: ортонормированный базис
заданы: ортонормированный базис
 (7.1)
(7.1)
и ещё какой-либо базис
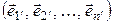 . (7.2)
. (7.2)
Для того чтобы базис (7.2) был ортонормированным, необходимо и достаточно, чтобы матрица Т перехода от (7.1) к (7.2) была унитарной для комплексного евклидова пространства, и ортогональной для действительного.
►Доказательство проводим для комплексного случая. Если  и
и  – матрицы Грама базисов (7.1) и (7.2) соответственно, то
– матрицы Грама базисов (7.1) и (7.2) соответственно, то 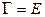 и
и  . Тогда
. Тогда
{(7.2) – ортонормированный} 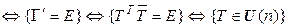 .◄
.◄
Некоторые свойства эрмитовых и симметричных матриц
Вспомним, что комплексная квадратная матрица А называется эрмитовой, если 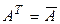 , а действительная квадратная матрица А – симметричной, если
, а действительная квадратная матрица А – симметричной, если 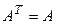 . Будем обозначать
. Будем обозначать  – множество всех эрмитовых матриц n -го порядка, а
– множество всех эрмитовых матриц n -го порядка, а  – множество всех действительных симметричных матриц n -го порядка. Очевидно,
– множество всех действительных симметричных матриц n -го порядка. Очевидно, 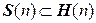 . Запишем некоторые свойства этих матриц, которые вы можете легко доказать в качестве упражнения.
. Запишем некоторые свойства этих матриц, которые вы можете легко доказать в качестве упражнения.
1º. 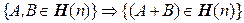 . 1'.
. 1'.  .
.
2º 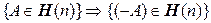 . 2'.
. 2'.  .
.
3º.  . 3'.
. 3'. 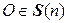 .
.
Свойства сопряженных операторов
1º.  , т. е. тождественный оператор сопряжен самому себе.
, т. е. тождественный оператор сопряжен самому себе.
►Очевидным образом вытекает из определения.◄
2º. 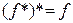 .
.
►  :
: 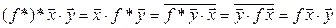 . Утверждение вытекает из леммы 7.1. ◄
. Утверждение вытекает из леммы 7.1. ◄
3º.  .
.
► 
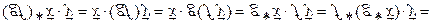
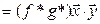
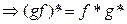 (объясните каждый шаг цепочки).◄
(объясните каждый шаг цепочки).◄
4º. Если оператор  имеет обратный и имеет сопряженный, то
имеет обратный и имеет сопряженный, то 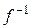 также имеет сопряженный, причем
также имеет сопряженный, причем  .
.
►  . Аналогично доказывается, что
. Аналогично доказывается, что  , значит,
, значит, 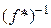 и есть
и есть  .◄
.◄
5º. 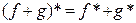 .
.
Это свойство вы можете легко доказать самостоятельно.
Если обозначить
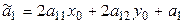 ,
, 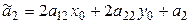 , (7.16)
, (7.16)
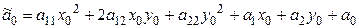 , (7.17)
, (7.17)
то (7.15) запишется в виде
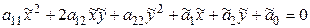 .
.
Сравнивая (7.13) и (7.16), (7.10) и (7.17), замечаем, что
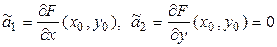 ,
, 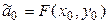 .
.
Завершает доказательство цепочка рассуждений:
{ 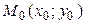 – центр симметрии Ф}
– центр симметрии Ф} 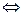 {
{ 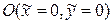 – центр симметрии Ф}
– центр симметрии Ф} 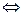
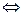 {
{ 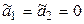 }
} 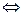 {
{ 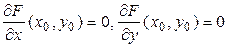 }.◄
}.◄
Вывод. Если с помощью параллельного переноса поместить начало координат в центр симметрии кривой второго порядка, то при этом: квадратичная часть ее уравнения не изменится; слагаемые первой степени пропадут; свободный член нового уравнения можно найти по формуле 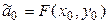 .
.
Точно так же доказываются аналогичные утверждения и для поверхностей второго порядка.
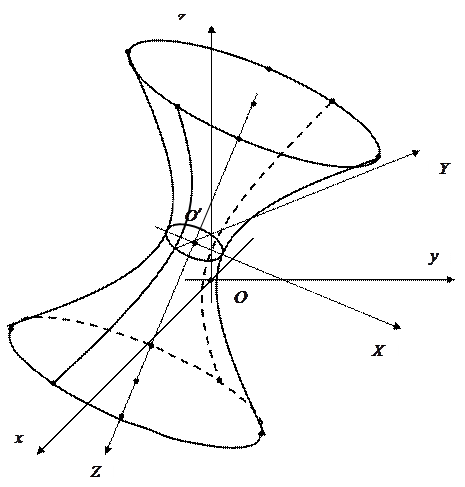
Пример. Определить видповерхности второго порядка
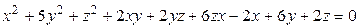 ,
,
приведя ее уравнение к каноническому виду, и нарисовать эту поверхность.
▼1. Проверяем существование центра симметрии. Для этого вычисляем частные производные и составляем систему вида (7.14):
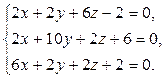
Решая эту систему, находим 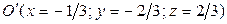 . С помощью параллельного переноса помещаем начало координат в центр поверхности
. С помощью параллельного переноса помещаем начало координат в центр поверхности 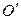 . При этом квадратичная часть уравнения не изменится, слагаемые первой степени пропадут, свободный член
. При этом квадратичная часть уравнения не изменится, слагаемые первой степени пропадут, свободный член 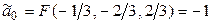 .
.
2. Приводим к каноническому виду квадратичную часть.
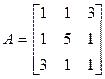 ;
; 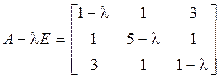 ,
,
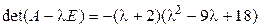 ;
; 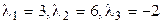 .
.
Рис.7.2
Записываем каноническое уравнение поверхности:
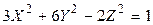
или
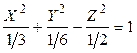
и видим, что это однополостный гиперболоид.
Находим базис, состоящий из собственных векторов, используя алгебраические дополнения:
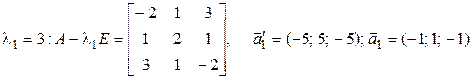 ;
; 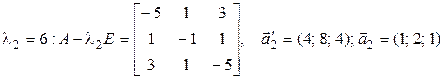 ;
; 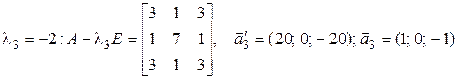 .
.
Заметим, что нормировать базисные векторы нет необходимости. Нормированные векторы были бы нам нужны для записи ортогонального преобразования переменных, приводящего квадратичную часть к каноническому виду. Но в данном примере это преобразование не используется. Остается поверхность нарисовать (рис. 7.2). ▲
Изометрии
Определение. Линейный оператор f евклидова пространства Е в себя называется изометрией, если он сохраняет скалярное произведение, т. е. если
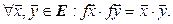 (7.18)
(7.18)
Изометрии в комплексном евклидовом пространстве называются унитарными операторами, а в действительном – ортогональными.
Теорема 7.10. Если l – собственное значение изометрии, то |l|=1.
►Пусть 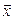 – собственный вектор изометрии
– собственный вектор изометрии 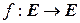 , l – его собственное значение. Положим
, l – его собственное значение. Положим 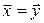 . Тогда: (7.18)
. Тогда: (7.18) 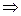
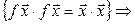
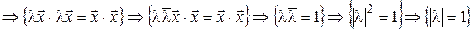 .◄
.◄
Замечание. Собственные значения ортогонального оператора равны 1 или –1. Ортогональный оператор в пространстве четной размерности может и не иметь собственных значений, но в пространстве нечетной размерности имеет хотя бы одно.
Теорема 7.11. Для того чтобы линейный оператор 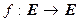 был изометрией, необходимо и достаточно, чтобы он сохранял длины векторов.
был изометрией, необходимо и достаточно, чтобы он сохранял длины векторов.
► Необходимость очевидна.
Достаточность (доказываем для комплексного случая). Пусть f сохраняет длины векторов, т. е. 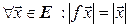 . Тогда
. Тогда 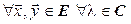 :
: 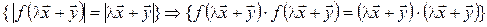
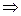
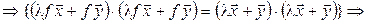
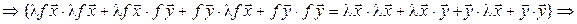
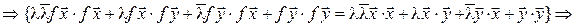
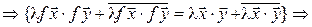
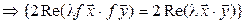 . (7.19)
. (7.19)
Так как (7.19) справедливо для всех комплексных l, то при l = 1 получаем 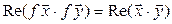 . Если же
. Если же 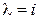 , то (7.19) принимает вид
, то (7.19) принимает вид 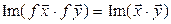 , и, таким образом, утверждение доказано.◄
, и, таким образом, утверждение доказано.◄
Следствие. Ортогональный оператор сохраняет углы между векторами.
Теорема 7.12. Изометрия 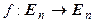 любой ортонормированный базис пространства
любой ортонормированный базис пространства  переводит в ортонормированный базис. Обратно, если линейный оператор
переводит в ортонормированный базис. Обратно, если линейный оператор 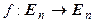 некоторый ортонормированный базис пространства
некоторый ортонормированный базис пространства  переводит в ортонормированный базис, то f – изометрия.
переводит в ортонормированный базис, то f – изометрия.
►Первое утверждение, очевидно, справедливо. Действительно, согласно определению, ортонормированный базис переходит в ортонормированную систему из n векторов, которая в силу теоремы 6.4 линейно независима и поэтому в n -мерном линейном пространстве является базисом.
Обратно. Пусть линейный оператор 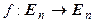 некоторый ортонормированный базис
некоторый ортонормированный базис
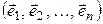 (7.20)
(7.20)
пространства  переводит в ортонормированный базис
переводит в ортонормированный базис
 , (7.21)
, (7.21)
и пусть 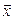 и
и 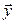 – произвольные векторы пространства
– произвольные векторы пространства  . Тогда каждый из векторов
. Тогда каждый из векторов 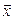 и
и 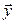 можно разложить по базису (7.20):
можно разложить по базису (7.20): 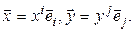 Так как базисы (7.20) и (7.21) ортонормированны, то
Так как базисы (7.20) и (7.21) ортонормированны, то 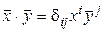 . Значит,
. Значит,
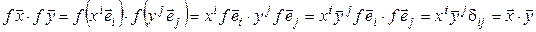
и, таким образом, f – изометрия.◄
Теорема 7.13. Для того чтобы линейный оператор 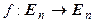 был изометрией, необходимо и достаточно, чтобы
был изометрией, необходимо и достаточно, чтобы  .
.
►На основании теоремы 7.2 любой линейный оператор 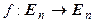 имеет сопряженный. Тогда:
имеет сопряженный. Тогда:
{ f – изометрия} 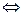
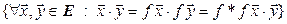
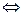
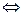 [лемма 7.1]
[лемма 7.1] 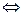 {
{ 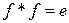 }. (7.22)
}. (7.22)
Если А – матрица оператора 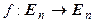 в некотором ортонормированном базисе пространства
в некотором ортонормированном базисе пространства  , то
, то 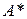 – матрица оператора
– матрица оператора 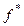 в том же базисе, и из (7.22) для изометрии получаем
в том же базисе, и из (7.22) для изометрии получаем
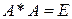 . (7.23)
. (7.23)
Из (7.23) вытекает, во-первых, что матрица изометрии невырождена, значит, любая изометрия 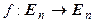 – невырожденный линейный оператор, причем
– невырожденный линейный оператор, причем 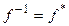 . Во-вторых, для того чтобы линейный оператор f комплексного евклидова пространства
. Во-вторых, для того чтобы линейный оператор f комплексного евклидова пространства  в себя был унитарным, необходимо и достаточно, чтобы его матрица в некотором, а значит, и в любом ортонормированном базисе пространства
в себя был унитарным, необходимо и достаточно, чтобы его матрица в некотором, а значит, и в любом ортонормированном базисе пространства  была унитарной. Для того чтобы линейный оператор f действительного евклидова пространства
была унитарной. Для того чтобы линейный оператор f действительного евклидова пространства  в себя был ортогональным, необходимо и достаточно, чтобы его матрица в некотором, а значит, и в любом ортонормированном базисе пространства
в себя был ортогональным, необходимо и достаточно, чтобы его матрица в некотором, а значит, и в любом ортонормированном базисе пространства 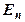 была ортогональной.◄
была ортогональной.◄
Ортогональные операторы
Виду пары квадратичных форм
Теорема 7.15. Пусть  и
и  – квадратичные формы на действительном линейном пространстве
– квадратичные формы на действительном линейном пространстве  , причем одна из них положительно определена. Тогда в
, причем одна из них положительно определена. Тогда в  существует базис, в котором обе квадратичные формы имеют канонический вид.
существует базис, в котором обе квадратичные формы имеют канонический вид.
►Пусть, например, квадратичная форма  положительно определена. Тогда соответствующая ей симметричная билинейная форма
положительно определена. Тогда соответствующая ей симметричная билинейная форма  тоже положительно определена. С помощью этой билинейной формы можно задать скалярное произведение на линейном пространстве
тоже положительно определена. С помощью этой билинейной формы можно задать скалярное произведение на линейном пространстве  и после этого оно превращается в евклидово пространство
и после этого оно превращается в евклидово пространство  . Согласно теореме 7.7, в
. Согласно теореме 7.7, в  существует ортонормированный базис
существует ортонормированный базис
 , (7.27)
, (7.27)
в котором форма  имеет канонический вид. Так как базис (7.27) ортонормированный, то
имеет канонический вид. Так как базис (7.27) ортонормированный, то 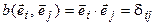 . Значит, квадратичная форма
. Значит, квадратичная форма  в базисе (7.27) имеет единичную матрицу, и поэтому форма
в базисе (7.27) имеет единичную матрицу, и поэтому форма  в этом базисе имеет нормальный вид. ◄
в этом базисе имеет нормальный вид. ◄
К каноническому виду
Пусть  и
и  – квадратичные формы на действительном линейном пространстве
– квадратичные формы на действительном линейном пространстве  , причем
, причем  положительно определена. Выберем в
положительно определена. Выберем в  какой-либо базис
какой-либо базис
 , (7.28)
, (7.28)
и обозначим  и
и 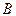 матрицы форм
матрицы форм  и
и  соответственно в этом базисе. В пространстве
соответственно в этом базисе. В пространстве  скалярное произведение зададим с помощью симметричной билинейной формы, соответствующей квадратичной форме
скалярное произведение зададим с помощью симметричной билинейной формы, соответствующей квадратичной форме  . Это значит, линейное пространство превращается в евклидово
. Это значит, линейное пространство превращается в евклидово  , а матрица Грама базиса (7.28) совпадает с
, а матрица Грама базиса (7.28) совпадает с 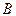 . Как и во всяком евклидовом пространстве, в
. Как и во всяком евклидовом пространстве, в  существует ортонормированный базис
существует ортонормированный базис
 . (7.29)
. (7.29)
Если  – матрица Грама базиса (7.28), а
– матрица Грама базиса (7.28), а  – матрица квадратичной формы
– матрица квадратичной формы  в этом базисе, то
в этом базисе, то  ,
,  . В силу ортонормированности базиса (7.29)
. В силу ортонормированности базиса (7.29)  , значит,
, значит,  , откуда получаем, что
, откуда получаем, что
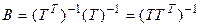 .
.
Согласно теореме 7.7, в  существует ортонормированный базис, в котором квадратичная форма
существует ортонормированный базис, в котором квадратичная форма  имеет канонический вид. Чтобы найти этот канонический вид, следует решить характеристическое уравнение
имеет канонический вид. Чтобы найти этот канонический вид, следует решить характеристическое уравнение
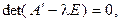 (7.30)
(7.30)
а чтобы найти векторы искомого базиса, следует для каждого собственного значения 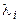 решить систему линейных уравнений
решить систему линейных уравнений
 , (7.31)
, (7.31)
где  – координатный столбец искомого собственного вектора в базисе (7.29). Но
– координатный столбец искомого собственного вектора в базисе (7.29). Но
{(7.30)}  {
{ 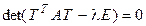 }
}  {
{  }
} 
 {
{  },
},
откуда вытекает, что (7.30) равносильно уравнению
 . (7.32)
. (7.32)
Система же (7.31) преобразуется так: {(7.31)}  {
{  }
} 
 {
{  }
}  {
{ 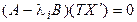 }. Если
}. Если  – координатный столбец искомого собственного вектора в базисе (7.28), то
– координатный столбец искомого собственного вектора в базисе (7.28), то 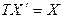 , значит, система (7.31) равносильна следующей:
, значит, система (7.31) равносильна следующей:
 . (7.33)
. (7.33)
Таким образом, диагональные элементы матрицы  – это корни
– это корни 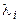 уравнения (7.32), а векторы искомого базиса – это решения системы линейных уравнений (7.33) для каждого из найденных значений
уравнения (7.32), а векторы искомого базиса – это решения системы линейных уравнений (7.33) для каждого из найденных значений 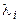 .
.
Из вышесказанного получаем следующее правило одновременного приведения пары квадратичных форм к каноническому виду:
1. Выписываем матрицы квадратичных форм и определяем, какая из них положительно определена. Матрицу положительно определенной квадратичной формы обозначаем 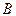 , а оставшуюся –
, а оставшуюся –  .
.
2. Составляем уравнение (7.32), которое также называется характеристическим, и находим его корни 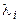 . Записываем канонический вид каждой из квадратичных форм:
. Записываем канонический вид каждой из квадратичных форм:  будет иметь нормальный вид, а коэффициенты канонического вида формы
будет иметь нормальный вид, а коэффициенты канонического вида формы  совпадают с найденными собственными значениями
совпадают с найденными собственными значениями 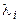 .
.
3. Находим ортогональный базис, решая систему линейных уравнений (7.33) при каждом из найденных собственных значений 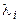 .
.
4. Нормируем каждый вектор (скалярное произведение задано формой  !).
!).
5. Составляем матрицу перехода от исходного базиса к ортонормированному базису из собственных векторов и по ней записываем линейное невырожденное преобразование переменных  .
.
Пример. Приведем одновременно к каноническому виду квадратичные формы
 и
и  .
.
▼1. Записываем матрицы обеих квадратичных форм:
 ,
,  .
.
Исследуем на знакоопределенность форму  по критерию Сильвестра:
по критерию Сильвестра:  . Итак, положительно определена форма
. Итак, положительно определена форма  . Значит,
. Значит,
 ,
,  .
.
2.

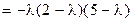 .
.
Записываем характеристическое уравнение 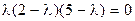 и находим его корни:
и находим его корни: 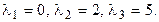
Канонический вид квадратичной формы  , а формы
, а формы  .
.
3.
 :
: 


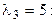


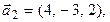

4.

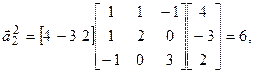




5. 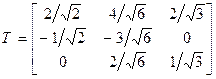 ;
; 
▲
ГЛАВА 7. ЛИНЕЙНЫЕ ОПЕРАТОРЫ
В ЕВКЛИДОВОМ ПРОСТРАНСТВЕ
§1. Некоторые сведения о матрицах
Ортогональные и унитарные матрицы
Определение. Комплексная квадратная матрица А называется унитарной, если 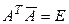 . Множество всех унитарных матриц n -го порядка будем обозначать
. Множество всех унитарных матриц n -го порядка будем обозначать 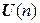 .
.
Следствия. 1. Модуль определителя унитарной матрицы равен 1.
►Из определения следует:  , значит,
, значит,  .◄
.◄
2. 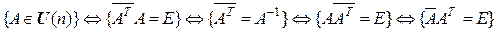 .
.
В силу равносильности любое из этих равенств может служить определением унитарной матрицы.
Определение. Действительная квадратная матрица 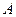 называется ортогональной, если
называется ортогональной, если 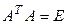 . Множество всех ортогональных матриц n -го порядка будем обозначать
. Множество всех ортогональных матриц n -го порядка будем обозначать 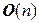 .
.
Следствия. 1.  .
.
2. Определитель ортогональной матрицы равен 1 или –1.
3.  .
.
Каждое из этих равенств опять же может служить определением ортогональной матрицы.


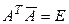 . Множество всех унитарных матриц n -го порядка будем обозначать
. Множество всех унитарных матриц n -го порядка будем обозначать  .
. , значит,
, значит,  .◄
.◄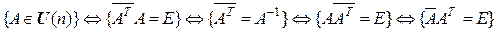 .
.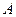 называется ортогональной, если
называется ортогональной, если 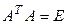 . Множество всех ортогональных матриц n -го порядка будем обозначать
. Множество всех ортогональных матриц n -го порядка будем обозначать 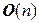 .
. .
. .
.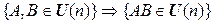 . 1'.
. 1'. 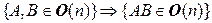 .
. . 2'.
. 2'. 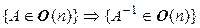 .
. 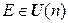 . 3'.
. 3'.  .
.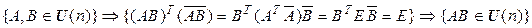 .◄
.◄ заданы: ортонормированный базис
заданы: ортонормированный базис (7.1)
(7.1)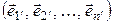 . (7.2)
. (7.2) и
и  – матрицы Грама базисов (7.1) и (7.2) соответственно, то
– матрицы Грама базисов (7.1) и (7.2) соответственно, то 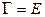 и
и  . Тогда
. Тогда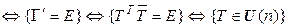 .◄
.◄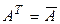 , а действительная квадратная матрица А – симметричной, если
, а действительная квадратная матрица А – симметричной, если 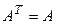 . Будем обозначать
. Будем обозначать  – множество всех эрмитовых матриц n -го порядка, а
– множество всех эрмитовых матриц n -го порядка, а  – множество всех действительных симметричных матриц n -го порядка. Очевидно,
– множество всех действительных симметричных матриц n -го порядка. Очевидно, 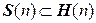 . Запишем некоторые свойства этих матриц, которые вы можете легко доказать в качестве упражнения.
. Запишем некоторые свойства этих матриц, которые вы можете легко доказать в качестве упражнения.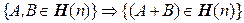 . 1'.
. 1'.  .
.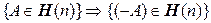 . 2'.
. 2'.  .
. . 3'.
. 3'. 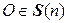 .
. , т. е. тождественный оператор сопряжен самому себе.
, т. е. тождественный оператор сопряжен самому себе.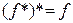 .
. :
: 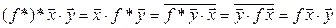 . Утверждение вытекает из леммы 7.1. ◄
. Утверждение вытекает из леммы 7.1. ◄ .
.
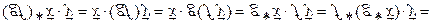
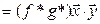
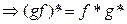 (объясните каждый шаг цепочки).◄
(объясните каждый шаг цепочки).◄ имеет обратный и имеет сопряженный, то
имеет обратный и имеет сопряженный, то 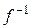 также имеет сопряженный, причем
также имеет сопряженный, причем  .
. . Аналогично доказывается, что
. Аналогично доказывается, что  , значит,
, значит, 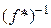 и есть
и есть  .◄
.◄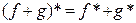 .
.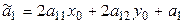 ,
, 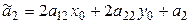 , (7.16)
, (7.16)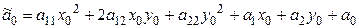 , (7.17)
, (7.17)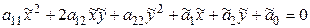 .
.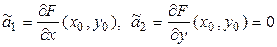 ,
, 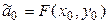 .
.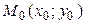 – центр симметрии Ф}
– центр симметрии Ф} 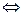 {
{ 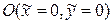 – центр симметрии Ф}
– центр симметрии Ф} 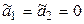 }
} 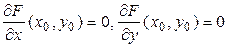 }.◄
}.◄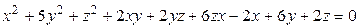 ,
,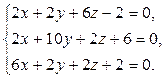
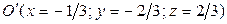 . С помощью параллельного переноса помещаем начало координат в центр поверхности
. С помощью параллельного переноса помещаем начало координат в центр поверхности 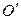 . При этом квадратичная часть уравнения не изменится, слагаемые первой степени пропадут, свободный член
. При этом квадратичная часть уравнения не изменится, слагаемые первой степени пропадут, свободный член 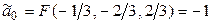 .
. ;
; 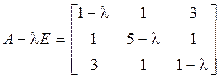 ,
,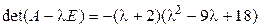 ;
; 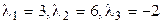 .
.
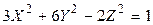
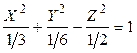
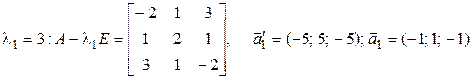 ;
; 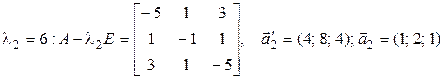 ;
; 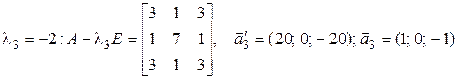 .
. (7.18)
(7.18) – собственный вектор изометрии
– собственный вектор изометрии 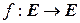 , l – его собственное значение. Положим
, l – его собственное значение. Положим 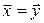 . Тогда: (7.18)
. Тогда: (7.18) 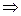
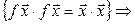
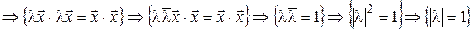 .◄
.◄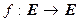 был изометрией, необходимо и достаточно, чтобы он сохранял длины векторов.
был изометрией, необходимо и достаточно, чтобы он сохранял длины векторов.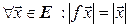 . Тогда
. Тогда 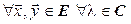 :
: 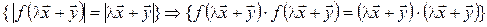
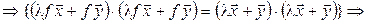
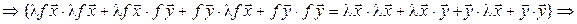
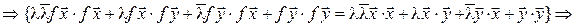
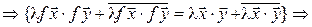
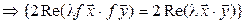 . (7.19)
. (7.19)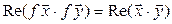 . Если же
. Если же 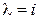 , то (7.19) принимает вид
, то (7.19) принимает вид 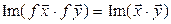 , и, таким образом, утверждение доказано.◄
, и, таким образом, утверждение доказано.◄ любой ортонормированный базис пространства
любой ортонормированный базис пространства  переводит в ортонормированный базис. Обратно, если линейный оператор
переводит в ортонормированный базис. Обратно, если линейный оператор 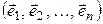 (7.20)
(7.20) , (7.21)
, (7.21)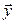 – произвольные векторы пространства
– произвольные векторы пространства 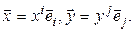 Так как базисы (7.20) и (7.21) ортонормированны, то
Так как базисы (7.20) и (7.21) ортонормированны, то 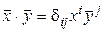 . Значит,
. Значит,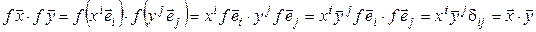
 .
.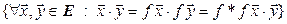
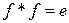 }. (7.22)
}. (7.22)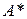 – матрица оператора
– матрица оператора 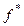 в том же базисе, и из (7.22) для изометрии получаем
в том же базисе, и из (7.22) для изометрии получаем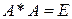 . (7.23)
. (7.23)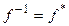 . Во-вторых, для того чтобы линейный оператор f комплексного евклидова пространства
. Во-вторых, для того чтобы линейный оператор f комплексного евклидова пространства  была ортогональной.◄
была ортогональной.◄ и
и  – квадратичные формы на действительном линейном пространстве
– квадратичные формы на действительном линейном пространстве  , причем одна из них положительно определена. Тогда в
, причем одна из них положительно определена. Тогда в  положительно определена. Тогда соответствующая ей симметричная билинейная форма
положительно определена. Тогда соответствующая ей симметричная билинейная форма  тоже положительно определена. С помощью этой билинейной формы можно задать скалярное произведение на линейном пространстве
тоже положительно определена. С помощью этой билинейной формы можно задать скалярное произведение на линейном пространстве  , (7.27)
, (7.27)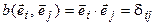 . Значит, квадратичная форма
. Значит, квадратичная форма  , (7.28)
, (7.28) и
и 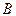 матрицы форм
матрицы форм  , а матрица Грама базиса (7.28) совпадает с
, а матрица Грама базиса (7.28) совпадает с  . (7.29)
. (7.29) – матрица Грама базиса (7.28), а
– матрица Грама базиса (7.28), а  – матрица квадратичной формы
– матрица квадратичной формы  ,
,  . В силу ортонормированности базиса (7.29)
. В силу ортонормированности базиса (7.29)  , значит,
, значит,  , откуда получаем, что
, откуда получаем, что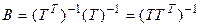 .
.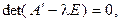 (7.30)
(7.30)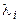 решить систему линейных уравнений
решить систему линейных уравнений , (7.31)
, (7.31) – координатный столбец искомого собственного вектора в базисе (7.29). Но
– координатный столбец искомого собственного вектора в базисе (7.29). Но {
{ 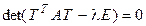 }
}  }
}  },
}, . (7.32)
. (7.32) }
}  }
} 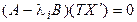 }. Если
}. Если  – координатный столбец искомого собственного вектора в базисе (7.28), то
– координатный столбец искомого собственного вектора в базисе (7.28), то 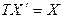 , значит, система (7.31) равносильна следующей:
, значит, система (7.31) равносильна следующей: . (7.33)
. (7.33) совпадают с найденными собственными значениями
совпадают с найденными собственными значениями  .
. и
и  .
. ,
,  .
. . Итак, положительно определена форма
. Итак, положительно определена форма  ,
,  .
.
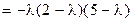 .
.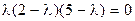 и находим его корни:
и находим его корни: 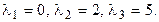
 , а формы
, а формы  .
. :
: 


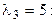


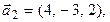


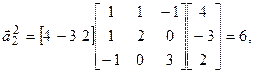




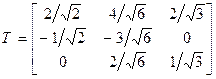 ;
;