второго порядка к каноническому вид у
Теорема 7.7. Для любой квадратичной формы на действительном евклидовом пространстве  в этом пространстве существует ортонормированный базис, в котором рассматриваемая квадратичная форма имеет канонический вид.
в этом пространстве существует ортонормированный базис, в котором рассматриваемая квадратичная форма имеет канонический вид.
► Пусть на евклидовом пространстве 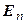 задана квадратичная форма k. Выберем в
задана квадратичная форма k. Выберем в 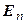 какой-либо ортонормированный базис
какой-либо ортонормированный базис
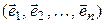 , (7.7)
, (7.7)
и пусть А – матрица квадратичной формы k в этом базисе. Тогда А – симметричная, а значит, существует такая ортогональная матрица Т, что матрица 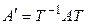 – диагональная. Так как матрица Т ортогональная, то по теореме 7.1 в
– диагональная. Так как матрица Т ортогональная, то по теореме 7.1 в 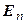 существует ортонормированный базис
существует ортонормированный базис
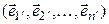 (7.8)
(7.8)
такой, что Т – матрица перехода от (7.7) к (7.8). Если Ã – матрица квадратичной формы k в базисе (7.8), то 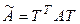 =
= 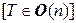 = =
= = 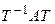 = А'. Матрица А' – диагональная и поэтому в базисе (7.8) квадратичная форма k имеет канонический вид.◄
= А'. Матрица А' – диагональная и поэтому в базисе (7.8) квадратичная форма k имеет канонический вид.◄
Замечание. Диагональными элементами матрицы А' являются собственные значения матрицы А.
Определение. Линейное невырожденное преобразование переменных называется ортогональным, если его матрица ортогональна.
Теорема 7.8. Любую действительную квадратичную форму можно привести к каноническому виду при помощи ортогонального преобразования переменных (иная формулировка теоремы 7.7).
Следствия. 1. Для того чтобы действительная квадратичная форма была положительно определенной необходимо и достаточно, чтобы все собственные значения ее матрицы были положительными.
2.Для любой поверхности второго порядка в трехмерном пространстве существует ортонормированная система координат, в которой эта поверхность задается каноническим уравнением.
Для любой кривой второго порядка на плоскости существует ортонормированная система координат, в которой эта кривая задается каноническим уравнением.
Пример. Определить вид кривой второго порядка, приведя ее уравнение к каноническому виду, и нарисовать эту кривую, если исходное уравнение кривой имеет вид
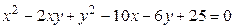 .
.
▼1. Приводим к каноническому виду квадратичную часть уравнения (т. е. квадратичную форму) с помощью ортогонального преобразования переменных. Для этого записываем матрицу этой квадратичной формы и находим ее собственные значения:
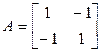 ,
, 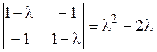 ,
, 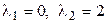 .
.
Для нахождения первого собственного вектора решаем систему линейных уравнений с матрицей 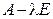 при
при  :
: 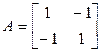 ,
, 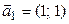 . Чтобы найти второй собственный вектор нет необходимости решать вторую систему. Достаточно вспомнить, что он ортогонален вектору
. Чтобы найти второй собственный вектор нет необходимости решать вторую систему. Достаточно вспомнить, что он ортогонален вектору 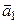 в силу симметричности матрицы А и что его координаты можно получить, как и в аналитической геометрии, переставив местами координаты вектора
в силу симметричности матрицы А и что его координаты можно получить, как и в аналитической геометрии, переставив местами координаты вектора 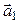 и в одной из них поменяв знак. Итак,
и в одной из них поменяв знак. Итак, 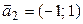 . Чтобы получить ортонормированный базис, векторы
. Чтобы получить ортонормированный базис, векторы 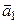 и
и 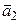 нормируем, т.е. делим каждый на его длину:
нормируем, т.е. делим каждый на его длину: 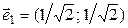 ,
, 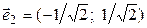 . Канонический вид квадратичной формы выглядит так:
. Канонический вид квадратичной формы выглядит так: 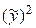 . Матрица перехода (она же матрица линейного невырожденного преобразования переменных) имеет вид
. Матрица перехода (она же матрица линейного невырожденного преобразования переменных) имеет вид
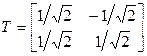 .
.
2. По матрице T записываем линейное невырожденное преобразование переменных:
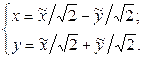 (7.9)
(7.9)
Подставляем выражение переменных по формулам (7.9) в исходное уравнение. При этом квадратичная часть переходит в известный нам канонический вид, свободный член не меняется, а чтобы узнать, как изменится линейная часть, следует непосредственно подставить формулы (7.9) в уравнение, раскрыть скобки и привести подобные.
Замечание. На самом деле коэффициенты линейной части есть линейные комбинации координат векторов 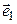 и
и 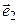 с теми же коэффициентами, что и в исходном уравнении. Например, коэффициент при
с теми же коэффициентами, что и в исходном уравнении. Например, коэффициент при 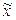 вычисляется так:
вычисляется так: 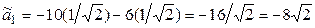 , а при
, а при 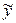 – так:
– так: 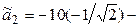
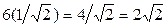 .
.
Таким образом, после преобразования (7.9) приходим к уравнению
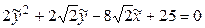 ,
,
которое равносильно следующему:
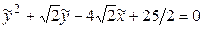 .
.
3. Преобразуем это уравнение:
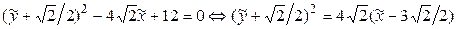
и применим к нему преобразование параллельного переноса:
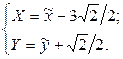
После этого уравнение кривой принимает вид
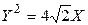 ,
,
откуда видно, что исследуемая кривая – парабола.
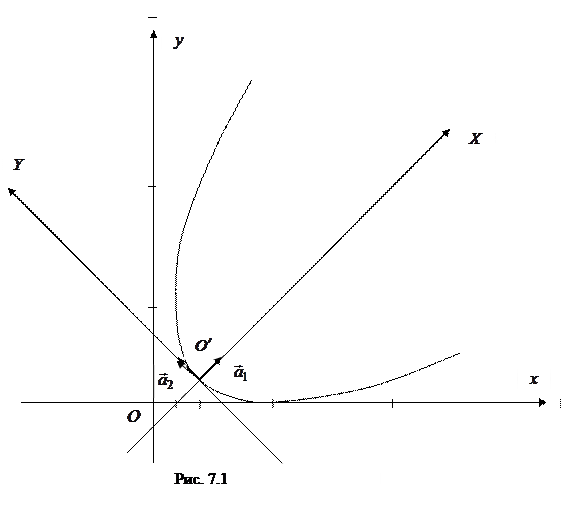
4. Приступаем к рисованию. На одном рисунке изображаем и старую систему координат, и новую. При преобразовании параллельного переноса начало координат переходит в точку
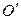
, в которой
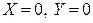
. Значит,
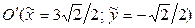
. Можно узнать координаты точки
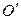
и в исходной системе координат. Для этого значения
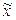
и
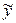
подставим в формулы (7.9):
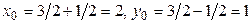
. Итак,
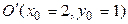
. Направление новых осей удобнее определять не по векторам
и
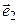
, а по векторам
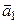
и
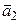
, так как они имеют целочисленные координаты (рис. 7.1).
Как видите, приведение к каноническому виду даже кривой второго порядка – занятие достаточно трудоемкое. Попробуем его упростить хотя бы в некоторых случаях.
Лемма 7.2. Для того чтобы начало координат было центром симметрии кривой второго порядка, необходимо и достаточно, чтобы коэффициенты при первых степенях переменных в ее уравнении равнялись нулю.
►Обозначим 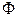 рассматриваемую кривую второго порядка. Пусть ее уравнение имеет вид:
рассматриваемую кривую второго порядка. Пусть ее уравнение имеет вид:
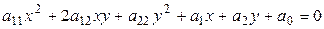 . (7.10)
. (7.10)
Необходимость.
{ О – центр симметрии кривой Ф} 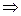
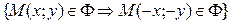
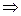
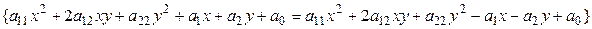
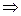
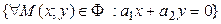 . (7.11)
. (7.11)
Рассмотрим два случая.
а) Кривая Ф не является сдвоенной прямой. Тогда на ней можно выбрать две точки 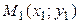 и
и 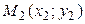 , не лежащие с началом координат на одной прямой. Из (7.11) получаем
, не лежащие с началом координат на одной прямой. Из (7.11) получаем
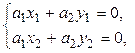 (7.12)
(7.12)
причем 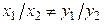 . Поэтому система (7.12) имеет единственное решение
. Поэтому система (7.12) имеет единственное решение 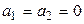 .
.
б) Ф – сдвоенная прямая 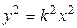 . Очевидно, утверждение истинно.
. Очевидно, утверждение истинно.
Достаточность очевидна, так как уравнение кривой Ф имеет вид
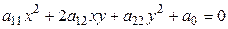 .◄
.◄
Обозначим 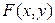 левую часть уравнения (7.10). Тогда
левую часть уравнения (7.10). Тогда
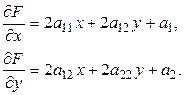 (7.13)
(7.13)
Теорема 7.9. Для того чтобы точка 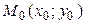 была центром симметрии кривой второго порядка
была центром симметрии кривой второго порядка 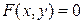 , необходимо и достаточно, чтобы координаты этой точки удовлетворяли системе линейных уравнений
, необходимо и достаточно, чтобы координаты этой точки удовлетворяли системе линейных уравнений
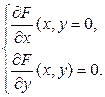 (7.14)
(7.14)
►Пусть 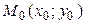 – центр симметрии кривой Ф с уравнением (7.10). Применим преобразование параллельного переноса
– центр симметрии кривой Ф с уравнением (7.10). Применим преобразование параллельного переноса 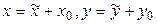 , которое помещает начало координат в точку
, которое помещает начало координат в точку 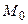 . При этом преобразовании уравнение (7.10) изменится так:
. При этом преобразовании уравнение (7.10) изменится так:
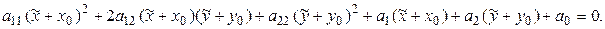 Последнее уравнение равносильно следующему:
Последнее уравнение равносильно следующему:
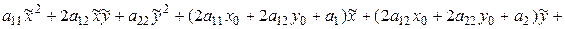
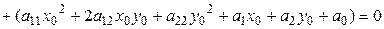 . (7.15)
. (7.15)
Если обозначить
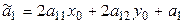 ,
, 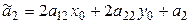 , (7.16)
, (7.16)
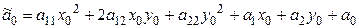 , (7.17)
, (7.17)
то (7.15) запишется в виде
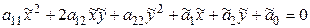 .
.
Сравнивая (7.13) и (7.16), (7.10) и (7.17), замечаем, что
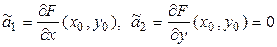 ,
, 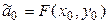 .
.
Завершает доказательство цепочка рассуждений:
{ 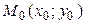 – центр симметрии Ф}
– центр симметрии Ф} 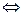 {
{ 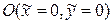 – центр симметрии Ф}
– центр симметрии Ф} 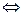
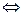 {
{ 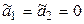 }
}  {
{ 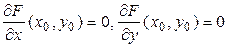 }.◄
}.◄
Вывод. Если с помощью параллельного переноса поместить начало координат в центр симметрии кривой второго порядка, то при этом: квадратичная часть ее уравнения не изменится; слагаемые первой степени пропадут; свободный член нового уравнения можно найти по формуле 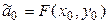 .
.
Точно так же доказываются аналогичные утверждения и для поверхностей второго порядка.
Пример. Определить видповерхности второго порядка
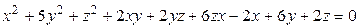 ,
,
приведя ее уравнение к каноническому виду, и нарисовать эту поверхность.
▼1. Проверяем существование центра симметрии. Для этого вычисляем частные производные и составляем систему вида (7.14):
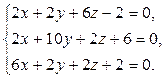
Решая эту систему, находим 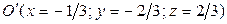 . С помощью параллельного переноса помещаем начало координат в центр поверхности
. С помощью параллельного переноса помещаем начало координат в центр поверхности 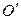 . При этом квадратичная часть уравнения не изменится, слагаемые первой степени пропадут, свободный член
. При этом квадратичная часть уравнения не изменится, слагаемые первой степени пропадут, свободный член 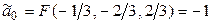 .
.
2. Приводим к каноническому виду квадратичную часть.
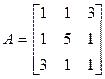 ;
; 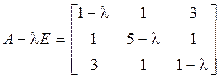 ,
,
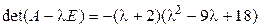 ;
; 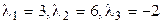 .
.
Рис.7.2
Записываем каноническое уравнение поверхности:
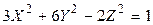
или
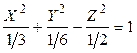
и видим, что это однополостный гиперболоид.
Находим базис, состоящий из собственных векторов, используя алгебраические дополнения:
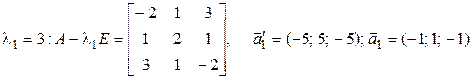 ;
; 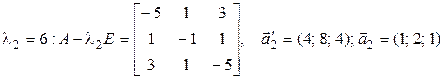 ;
; 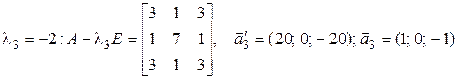 .
.
Заметим, что нормировать базисные векторы нет необходимости. Нормированные векторы были бы нам нужны для записи ортогонального преобразования переменных, приводящего квадратичную часть к каноническому виду. Но в данном примере это преобразование не используется. Остается поверхность нарисовать (рис. 7.2). ▲
Изометрии
Определение. Линейный оператор f евклидова пространства Е в себя называется изометрией, если он сохраняет скалярное произведение, т. е. если
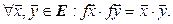 (7.18)
(7.18)
Изометрии в комплексном евклидовом пространстве называются унитарными операторами, а в действительном – ортогональными.
Теорема 7.10. Если l – собственное значение изометрии, то |l|=1.
►Пусть 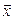 – собственный вектор изометрии
– собственный вектор изометрии 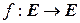 , l – его собственное значение. Положим
, l – его собственное значение. Положим 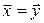 . Тогда: (7.18)
. Тогда: (7.18) 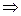
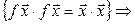
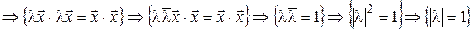 .◄
.◄
Замечание. Собственные значения ортогонального оператора равны 1 или –1. Ортогональный оператор в пространстве четной размерности может и не иметь собственных значений, но в пространстве нечетной размерности имеет хотя бы одно.
Теорема 7.11. Для того чтобы линейный оператор 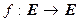 был изометрией, необходимо и достаточно, чтобы он сохранял длины векторов.
был изометрией, необходимо и достаточно, чтобы он сохранял длины векторов.
► Необходимость очевидна.
Достаточность (доказываем для комплексного случая). Пусть f сохраняет длины векторов, т. е. 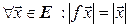 . Тогда
. Тогда 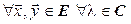 :
: 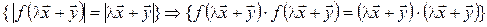
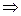
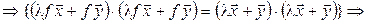
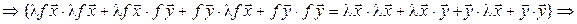
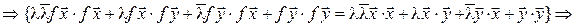
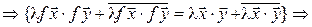
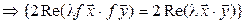 . (7.19)
. (7.19)
Так как (7.19) справедливо для всех комплексных l, то при l = 1 получаем 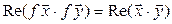 . Если же
. Если же 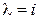 , то (7.19) принимает вид
, то (7.19) принимает вид 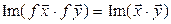 , и, таким образом, утверждение доказано.◄
, и, таким образом, утверждение доказано.◄
Следствие. Ортогональный оператор сохраняет углы между векторами.
Теорема 7.12. Изометрия 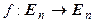 любой ортонормированный базис пространства
любой ортонормированный базис пространства  переводит в ортонормированный базис. Обратно, если линейный оператор
переводит в ортонормированный базис. Обратно, если линейный оператор 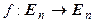 некоторый ортонормированный базис пространства
некоторый ортонормированный базис пространства  переводит в ортонормированный базис, то f – изометрия.
переводит в ортонормированный базис, то f – изометрия.
►Первое утверждение, очевидно, справедливо. Действительно, согласно определению, ортонормированный базис переходит в ортонормированную систему из n векторов, которая в силу теоремы 6.4 линейно независима и поэтому в n -мерном линейном пространстве является базисом.
Обратно. Пусть линейный оператор 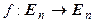 некоторый ортонормированный базис
некоторый ортонормированный базис
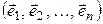 (7.20)
(7.20)
пространства  переводит в ортонормированный базис
переводит в ортонормированный базис
 , (7.21)
, (7.21)
и пусть 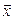 и
и 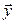 – произвольные векторы пространства
– произвольные векторы пространства  . Тогда каждый из векторов
. Тогда каждый из векторов 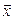 и
и 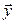 можно разложить по базису (7.20):
можно разложить по базису (7.20): 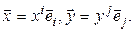 Так как базисы (7.20) и (7.21) ортонормированны, то
Так как базисы (7.20) и (7.21) ортонормированны, то 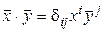 . Значит,
. Значит,
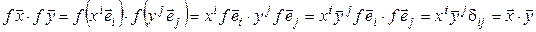
и, таким образом, f – изометрия.◄
Теорема 7.13. Для того чтобы линейный оператор 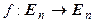 был изометрией, необходимо и достаточно, чтобы
был изометрией, необходимо и достаточно, чтобы  .
.
►На основании теоремы 7.2 любой линейный оператор 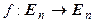 имеет сопряженный. Тогда:
имеет сопряженный. Тогда:
{ f – изометрия} 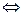
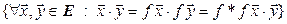
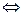
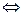 [лемма 7.1]
[лемма 7.1] 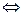 {
{ 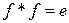 }. (7.22)
}. (7.22)
Если А – матрица оператора 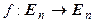 в некотором ортонормированном базисе пространства
в некотором ортонормированном базисе пространства  , то
, то 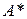 – матрица оператора
– матрица оператора 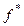 в том же базисе, и из (7.22) для изометрии получаем
в том же базисе, и из (7.22) для изометрии получаем
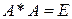 . (7.23)
. (7.23)
Из (7.23) вытекает, во-первых, что матрица изометрии невырождена, значит, любая изометрия 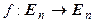 – невырожденный линейный оператор, причем
– невырожденный линейный оператор, причем 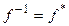 . Во-вторых, для того чтобы линейный оператор f комплексного евклидова пространства
. Во-вторых, для того чтобы линейный оператор f комплексного евклидова пространства  в себя был унитарным, необходимо и достаточно, чтобы его матрица в некотором, а значит, и в любом ортонормированном базисе пространства
в себя был унитарным, необходимо и достаточно, чтобы его матрица в некотором, а значит, и в любом ортонормированном базисе пространства  была унитарной. Для того чтобы линейный оператор f действительного евклидова пространства
была унитарной. Для того чтобы линейный оператор f действительного евклидова пространства  в себя был ортогональным, необходимо и достаточно, чтобы его матрица в некотором, а значит, и в любом ортонормированном базисе пространства
в себя был ортогональным, необходимо и достаточно, чтобы его матрица в некотором, а значит, и в любом ортонормированном базисе пространства 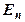 была ортогональной.◄
была ортогональной.◄


 в этом пространстве существует ортонормированный базис, в котором рассматриваемая квадратичная форма имеет канонический вид.
в этом пространстве существует ортонормированный базис, в котором рассматриваемая квадратичная форма имеет канонический вид. , (7.7)
, (7.7)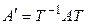 – диагональная. Так как матрица Т ортогональная, то по теореме 7.1 в
– диагональная. Так как матрица Т ортогональная, то по теореме 7.1 в 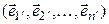 (7.8)
(7.8)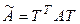 =
= 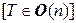 = =
= = 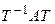 = А'. Матрица А' – диагональная и поэтому в базисе (7.8) квадратичная форма k имеет канонический вид.◄
= А'. Матрица А' – диагональная и поэтому в базисе (7.8) квадратичная форма k имеет канонический вид.◄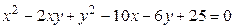 .
.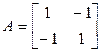 ,
, 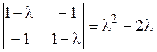 ,
, 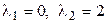 .
.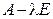 при
при 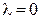 :
: 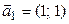 . Чтобы найти второй собственный вектор нет необходимости решать вторую систему. Достаточно вспомнить, что он ортогонален вектору
. Чтобы найти второй собственный вектор нет необходимости решать вторую систему. Достаточно вспомнить, что он ортогонален вектору 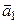 в силу симметричности матрицы А и что его координаты можно получить, как и в аналитической геометрии, переставив местами координаты вектора
в силу симметричности матрицы А и что его координаты можно получить, как и в аналитической геометрии, переставив местами координаты вектора 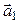 и в одной из них поменяв знак. Итак,
и в одной из них поменяв знак. Итак, 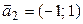 . Чтобы получить ортонормированный базис, векторы
. Чтобы получить ортонормированный базис, векторы 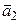 нормируем, т.е. делим каждый на его длину:
нормируем, т.е. делим каждый на его длину: 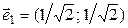 ,
, 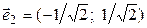 . Канонический вид квадратичной формы выглядит так:
. Канонический вид квадратичной формы выглядит так: 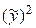 . Матрица перехода (она же матрица линейного невырожденного преобразования переменных) имеет вид
. Матрица перехода (она же матрица линейного невырожденного преобразования переменных) имеет вид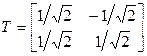 .
.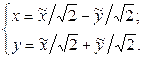 (7.9)
(7.9)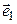 и
и 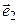 с теми же коэффициентами, что и в исходном уравнении. Например, коэффициент при
с теми же коэффициентами, что и в исходном уравнении. Например, коэффициент при 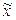 вычисляется так:
вычисляется так: 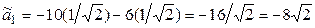 , а при
, а при 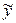 – так:
– так: 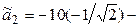
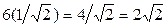 .
.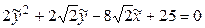 ,
,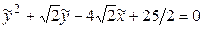 .
.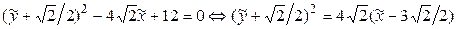
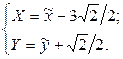
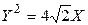 ,
,
 , в которой
, в которой  . Значит,
. Значит,  . Можно узнать координаты точки
. Можно узнать координаты точки 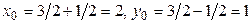 . Итак,
. Итак, 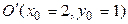 . Направление новых осей удобнее определять не по векторам
. Направление новых осей удобнее определять не по векторам  рассматриваемую кривую второго порядка. Пусть ее уравнение имеет вид:
рассматриваемую кривую второго порядка. Пусть ее уравнение имеет вид: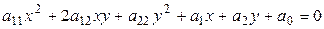 . (7.10)
. (7.10)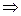
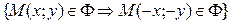
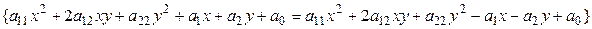
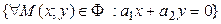 . (7.11)
. (7.11)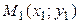 и
и 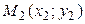 , не лежащие с началом координат на одной прямой. Из (7.11) получаем
, не лежащие с началом координат на одной прямой. Из (7.11) получаем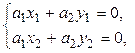 (7.12)
(7.12)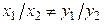 . Поэтому система (7.12) имеет единственное решение
. Поэтому система (7.12) имеет единственное решение 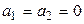 .
.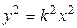 . Очевидно, утверждение истинно.
. Очевидно, утверждение истинно.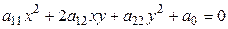 .◄
.◄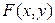 левую часть уравнения (7.10). Тогда
левую часть уравнения (7.10). Тогда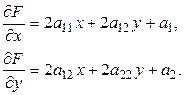 (7.13)
(7.13)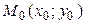 была центром симметрии кривой второго порядка
была центром симметрии кривой второго порядка 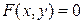 , необходимо и достаточно, чтобы координаты этой точки удовлетворяли системе линейных уравнений
, необходимо и достаточно, чтобы координаты этой точки удовлетворяли системе линейных уравнений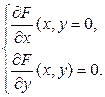 (7.14)
(7.14)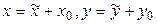 , которое помещает начало координат в точку
, которое помещает начало координат в точку 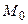 . При этом преобразовании уравнение (7.10) изменится так:
. При этом преобразовании уравнение (7.10) изменится так: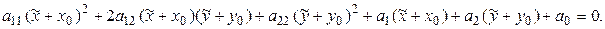 Последнее уравнение равносильно следующему:
Последнее уравнение равносильно следующему: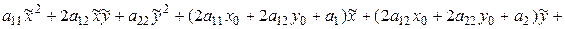
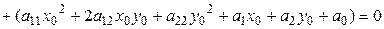 . (7.15)
. (7.15)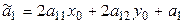 ,
, 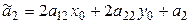 , (7.16)
, (7.16)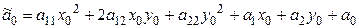 , (7.17)
, (7.17)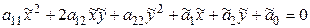 .
.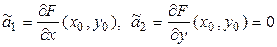 ,
, 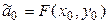 .
. {
{ 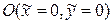 – центр симметрии Ф}
– центр симметрии Ф} 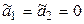 }
} 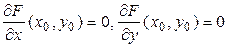 }.◄
}.◄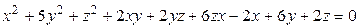 ,
,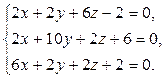
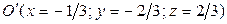 . С помощью параллельного переноса помещаем начало координат в центр поверхности
. С помощью параллельного переноса помещаем начало координат в центр поверхности 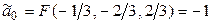 .
. ;
; 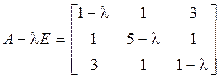 ,
,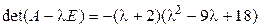 ;
; 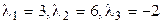 .
.
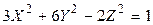
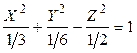
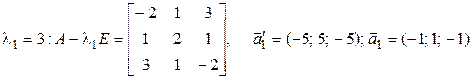 ;
; 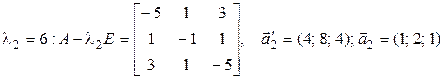 ;
; 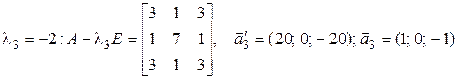 .
.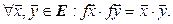 (7.18)
(7.18)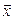 – собственный вектор изометрии
– собственный вектор изометрии 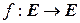 , l – его собственное значение. Положим
, l – его собственное значение. Положим 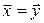 . Тогда: (7.18)
. Тогда: (7.18) 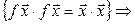
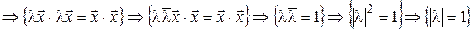 .◄
.◄ был изометрией, необходимо и достаточно, чтобы он сохранял длины векторов.
был изометрией, необходимо и достаточно, чтобы он сохранял длины векторов.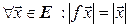 . Тогда
. Тогда 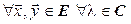 :
: 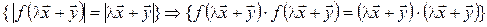
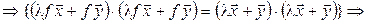
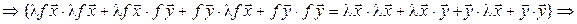
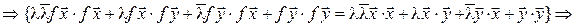
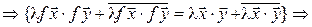
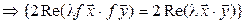 . (7.19)
. (7.19)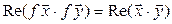 . Если же
. Если же 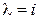 , то (7.19) принимает вид
, то (7.19) принимает вид 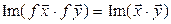 , и, таким образом, утверждение доказано.◄
, и, таким образом, утверждение доказано.◄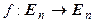 любой ортонормированный базис пространства
любой ортонормированный базис пространства  переводит в ортонормированный базис. Обратно, если линейный оператор
переводит в ортонормированный базис. Обратно, если линейный оператор 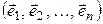 (7.20)
(7.20) , (7.21)
, (7.21)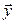 – произвольные векторы пространства
– произвольные векторы пространства 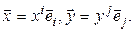 Так как базисы (7.20) и (7.21) ортонормированны, то
Так как базисы (7.20) и (7.21) ортонормированны, то 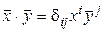 . Значит,
. Значит,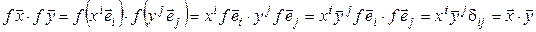
 .
.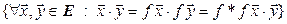
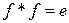 }. (7.22)
}. (7.22)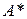 – матрица оператора
– матрица оператора 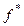 в том же базисе, и из (7.22) для изометрии получаем
в том же базисе, и из (7.22) для изометрии получаем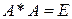 . (7.23)
. (7.23)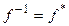 . Во-вторых, для того чтобы линейный оператор f комплексного евклидова пространства
. Во-вторых, для того чтобы линейный оператор f комплексного евклидова пространства  была ортогональной.◄
была ортогональной.◄