Уравнение регрессии в виде гиперболы

В общем случае уравнение гиперболы имеет вид y = a / x + b.

Пусть исходная функция y = f (x) варианта задания имеет вид, показанный в таблице в диапазоне ячеек A 7: B 18, рис. 4.9.1.

Построим точечный график функции Гиперболическая регрессия y = f (x).

В строке 21 создадим шапку таблицы, как показано на рис. 4.9.1.

В ячейку B 30 запишем произвольную константу 1, а в ячейку C 30 - произвольную константу 2.

 

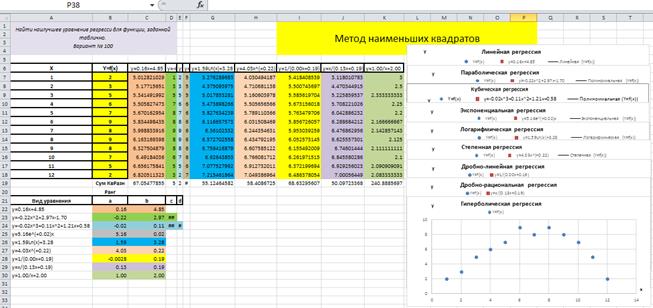
Рис. 4.9.1

В ячейку A 30 запишем оператор присваивания для сцепленных символьных констант:

="y="&ТЕКСТ(B30;"0.00")&"/x"&ЕСЛИ(C30<0;ТЕКСТ(C30;"0.00");"+"&ТЕКСТ(C30;"0.00"))

Ячейке K 6 присвоим такое же значение, какое приобретает ячейка A 30, то есть K 6 = A 30.

Тогда, в соответствии с выбранными коэффициентами в ячейках B 30=1 и C 30=2, в ячейках A 30 и K 6 получим результат y = 1.00/ x + 2.00.

Запишем в ячейку K 7 уравнение гиперболы с коэффициентами, взятыми в абсолютной адресации из ячеек B 30 и C 30, то есть =$B$30/A7+$C$30, в качестве аргумента X берётся значение ячейки A7 исходной таблицы.

Скопируем закон преобразования информации ячейки K 7 до ячейки K 18 включительно.

В результате получим спектр значений функции y = 1/ x + 2 на спектре аргументов X в диапазоне значений ячеек A 7: A 18, рис. 4.9.1.

В ячейку K 19, используя мастер функций f_x, запишем результат вычисления функции =СУММКВРАЗН(B7:B18;K7:K18), рис. 4.9.2.

 

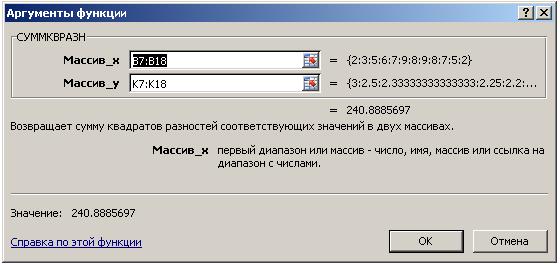
Рис. 4.9.2

Примечание: обозначение Массив_ x и Массив_ y, рис. 4.9.2, математическое и не совпадает с обозначениями выполняемого задания.

Добавим на точечный рисунок исходной таблицы уравнение гиперболы y = 1/ x + 2, рис. 4.9.3.

 

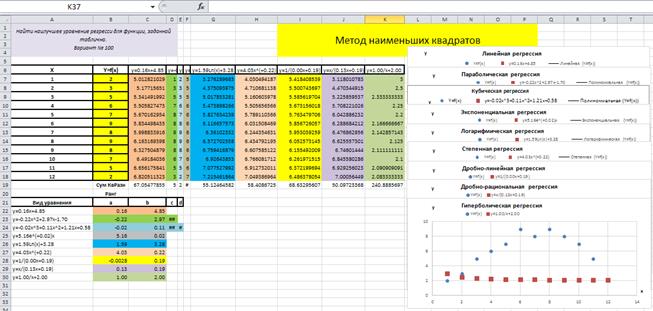
Рис. 4.9.3

Заметим, что это уравнение гиперболической регрессии, с произвольными значениями коэффициентов a =1 и b =2.

Соответствие этого уравнения регрессии исходному распределению оценено с помощью вычисления функции суммы квадратов разностей, значение которой составляет 240.8885697.

Для определения оптимальных значений коэффициентов a и b воспользуемся функцией Поиск решения:

– установим курсор в ячейку K 19;

– последовательно, выбирая Разработчик, Данные, Поиск решения, вызвать окно Параметры поиска решения, в котором установить параметры, как показано на рис. 4.9.4, и нажать кнопку Найти решение;

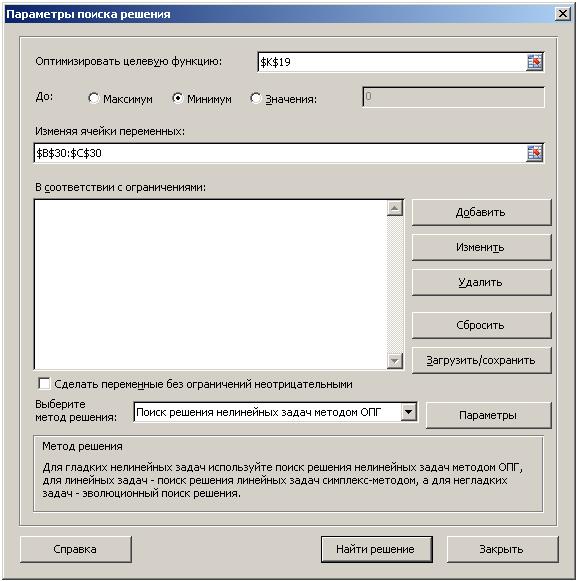
Рис. 4.9.4

– увидеть, как в ячейке B 30 установится значение - 5.66, в ячейке C 30 – 7.38, в ячейке K 19 – 46.48573172, рис. 4.9.5;

 

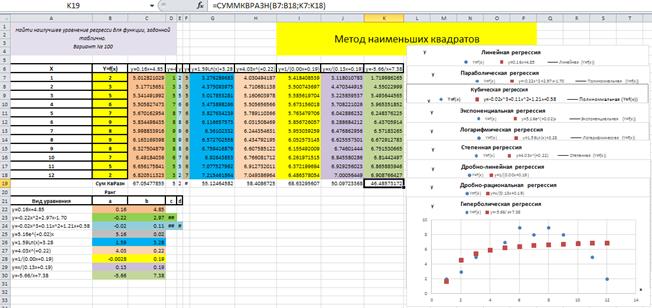
Рис. 4.9.5

Это означает, что гипербола с коэффициентами a = - 5.66 и b = 7.38 отобразится на графике Гиперболическая регрессия, как показано на рис. 4.9.5, при этом значение суммы квадратов разностей будет минимально и равно 46.48573172.

Таким образом, коэффициенты для гиперболического уравнения регрессии определены и для исходного задания уравнение имеет вид y = - 5.66/ x + 7.38.

Так как в библиотеке линий тренда отсутствует гиперболическая функция, то проверить правильность решения добавлением линии тренда не представляется возможным.

На рис. 4.9.6 показан результирующий график использования в качестве уравнения регрессии гиперболической функции y = - 5.66/ x + 7.38 для исходного варианта задания y = f (x).

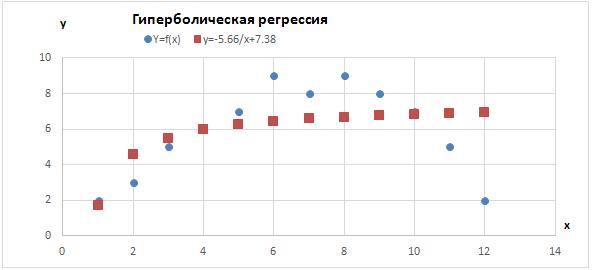
Рис. 4.9.6

 

Оценка результатов

Для оценки полученных результатов, то есть для определения уравнения регрессии наилучшим образом соответствующего исходному табличному заданию функции y = f (x) необходимо сравнить рассмотренные уравнения регрессии по вычисленным значениям сумм квадратов разностей или по значениям коэффициентов детерминации. Значения сумм квадратов разностей находятся в ячейках C 19: K 19.

При выполнении сравнения целесообразно использовать имеющуюся в среде Excel функцию РАНГ.

Для чего:

– установить курсор в ячейку B 20 и записать в неё символьную константу “ Ранг ”, рис. 4.10.1;

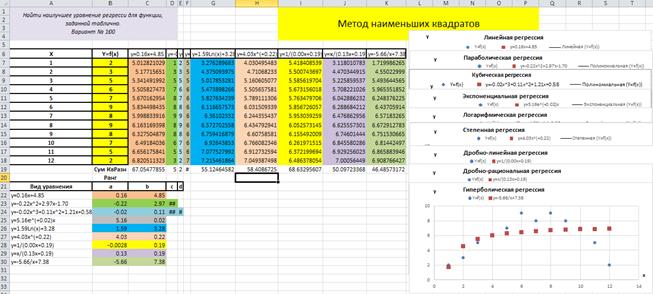
Рис. 4.10.1

– установить курсор в ячейку C 20 и вызвать с помощью мастера функций f_x функцию РАНГ, рис. 4.10.2, (столбцы D, C и F сжаты);

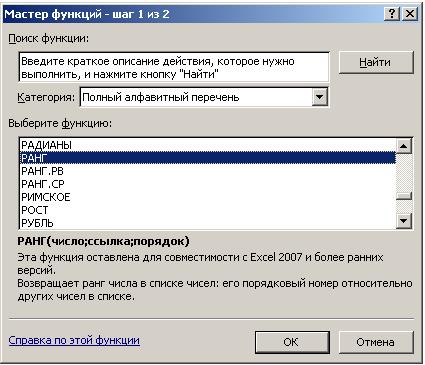
Рис. 4.10.2

– в появившемся окне Аргументы функции в окне Число ввести адрес ячейки C 19, в окне Ссылка ввести диапазон ячеек $ C $19:$ K $19, в окне Порядок ввести константу, например, 2 и нажать кнопку ОК, рис. 4.10.3;

 

Рис. 4.10.3

    Адрес ячейки C 19 указывается потому, что в этой ячейке находится число, в данном случае это 67.05477855, место которого (Ранг) мы хотим определить среди всех чисел, находящихся в ячейках диапазона $ C $19:$ K $19 (обязательно указывать в абсолютной адресации).

    Константа 2 определяет порядок ранжирования по убыванию или по возрастанию, в данном случае на первое место (Ранг 1) помещается самое маленькое число.

– в ячейке C 20 появится число 7, это означает, что число 67.05477855 занимает седьмое место (имеет ранг 7) по возрастанию среди всех чисел диапазона ячеек $ C $19:$ K $19, рис. 4.10.4;

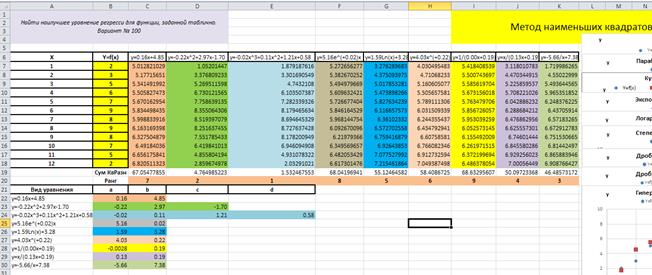
Рис. 4.10.4

– скопировать функцию Ранг ячейки C 20 на весь диапазон ячеек C 20: K 20, в результате получим значения рангов для всех чисел, находящихся в диапазоне ячеек $ C $19:$ K $19, рис. 4.10.4.

Для удобства результаты ранжирования можно объединить в таблицу, рис. 4.10.5.

Рис. 4.10.5

    Исходя из таблицы рис. 4.10.5, можно сделать вывод о том, что для рассмотренного варианта задания из всех девяти исследованных уравнений регрессии исходному табличному заданию функции y = f (x) наилучшим образом соответствует уравнение кубического полинома    y =-0.02 x ³ +0.11 x ² +1.21 x +0.58, так как вычисленная для него сумма квадратов разностей имеет минимальное значение 1.532467553.

    Этот результат подтверждается и значением коэффициента детерминации, величина которого 0.9784, то есть максимальна.

    Результат выполнения заданного варианта показан на рис. 4.10.6.

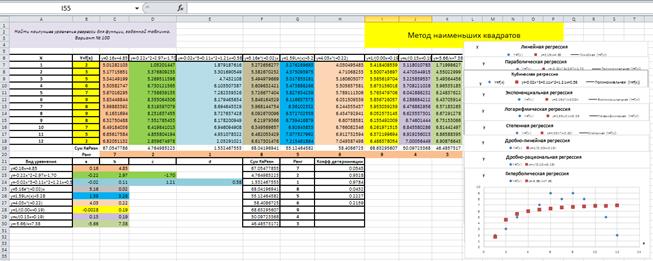
Рис. 4.10.6

 

Рекомендуемая литература

 

1. Никифоров С.Н., Информатика для I курса. Ч. I: учебное пособие по выполнению лабораторных работ по курсу “Информатика”, СПбГАСУ, СПб., 2011. – 100 c.

2. Никифоров С.Н., Информатика для I курса. Ч. II: учебное пособие по выполнению лабораторных работ по курсу “Информатика”, СПбГАСУ, СПб., 2015. – 100 c.

3. Гарнаев А. Ю., Использование MS Excel и VBA в экономике и финансах, СПб.: БХВ – Санкт-Петербург, 1999. – 336 с., ил.

4. Гарбер Г.З. Основы программирования на Visual Basic и VBA в Excel 2007, Москва, Солон-Пресс, 2008, 192 с.

 

 

СОДЕРЖАНИЕ

ВВЕДЕНИЕ.. 3

1. Вычисление определённого интеграла. 4

1.1 Метод прямоугольников. 4

1.2 Метод трапеций. 7

1.3 Метод Симпсона. 10

1.4 Использование пользовательской формы UserForm.. 12

1.5 Калькулятор для вычисления определённых интегралов. 15

1.6 Создание надписи (изображения) на объекте OptionButton. 22

1.7 Вывод. 23

2. Решение нелинейных уравнений. 24

2.1 Метод половинного деления (Дихотомия) 24

2.2 Метод Ньютона (метод касательных) 27

2.3 Метод хорд. 30

2.4 Решение второго нелинейного уравнения. 31

2.5 Калькулятор для решения нелинейных уравнений. 36

2.6 Создание надписи (изображения) на объекте OptionButton. 42

2.7 Вывод. 43

3. Интерполяция. 44

3.1 Нахождение коэффициентов полинома решением СЛАУ.. 44

3.2 Интерполяционный многочлен Лагранжа. 48

3.3 Интерполяционный многочлен Ньютона. 52

3.4 Калькулятор для вычисления значений интерполяционных полиномов. 55

4. Метод наименьших квадратов. 71

4.1 Линейное уравнение регрессии. 72

4.2 Параболическое уравнение регрессии. 78

4.3 Уравнение регрессии в виде полинома третьей степени. 84

4.4 Уравнение регрессии в виде экспоненциальной функции. 90

4.5 Логарифмическое уравнение регрессии. 96

4.6 Степенное уравнение регрессии. 102

4.7 Дробно-линейное уравнение регрессии. 108

4.8 Дробно-рациональное уравнение регрессии. 112

4.9 Уравнение регрессии в виде гиперболы.. 116

4.10 Оценка результатов. 121

Рекомендуемая литература. 124

 

Учебное издание

 

Никифоров Сергей Николаевич

 

Прикладное программирование

Учебное пособие

 

 

Редактор

Корректоры

Компьютерная верстка

 

 

Подписано к печати ХХ.ХХ.14. Формат 60х84 1/16. Бум. Офсетная

Усл. печ. л. ХХ,Х. Тираж 150 экз. Заказ 168. “С” 89

 

 

Даша

 

[1] Криволинейная трапеция – такая трапеция, у которой одна сторона отрезок параболы.

[2] Если раздел Разработчик отсутствует, то добавить его, пройдя по цепочке Файл, Параметры, Настройка ленты, Разработчик

[3] Если раздел Поиск решения отсутствует, то добавить его, пройдя по цепочке Разработчик, Надстройки, Поиск решения

[4] Коэффициент детерминации