

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...

Адаптации растений и животных к жизни в горах: Большое значение для жизни организмов в горах имеют степень расчленения, крутизна и экспозиционные различия склонов...
Топ:
История развития методов оптимизации: теорема Куна-Таккера, метод Лагранжа, роль выпуклости в оптимизации...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного хозяйства...
Проблема типологии научных революций: Глобальные научные революции и типы научной рациональности...
Интересное:
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Лечение прогрессирующих форм рака: Одним из наиболее важных достижений экспериментальной химиотерапии опухолей, начатой в 60-х и реализованной в 70-х годах, является...
Дисциплины:
|
из
5.00
|
Заказать работу |
Конспект лекций по
Числовым рядам
Числовые ряды
Определение: Рассмотрим бесконечную числовую последовательность:
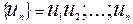 числовым рядом называется выражение
числовым рядом называется выражение 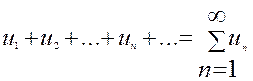 , где
, где 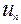 – общий член ряда.
– общий член ряда.
Пример:
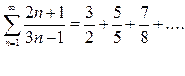 -знакоположительный ряд
-знакоположительный ряд
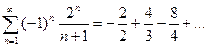 -знакочередующийся ряд
-знакочередующийся ряд
Последовательность 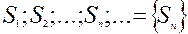 , где
, где 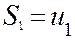 ;
; 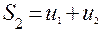 ;
; 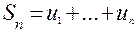 - последовательность частичных сумм ряда.
- последовательность частичных сумм ряда.
Каждая частичная сумма содержит конечное число слагаемых.
Числовой ряд 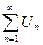 называется сходящимся, если существует конечный
называется сходящимся, если существует конечный
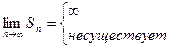 , то ряд называется расходящимся и суммы S не имеют.
, то ряд называется расходящимся и суммы S не имеют.
1)Рассмотрим ряд из членов геометрической прогрессии.
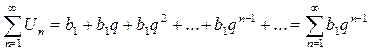 , где n – частичная сумма ряда
, где n – частичная сумма ряда 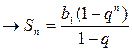 - сумма n первых членов геометрической прогрессии.
- сумма n первых членов геометрической прогрессии.
Рассмотрим 3 случая:
1) 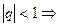 геометрическая прогрессия убывающая.
геометрическая прогрессия убывающая.
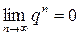
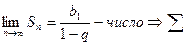 сходится и имеет сумму
сходится и имеет сумму 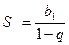
2) 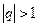
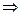
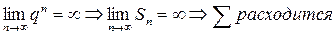
3) 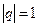
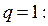
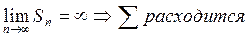
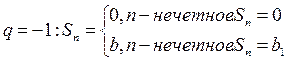
 = не существует – ряд расходится.
= не существует – ряд расходится.
Вывод: ряд из членов геометрической прогрессии сходится если 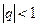 и расходится
и расходится 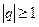

Элементарные свойства рядов
1) Если 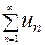 (1) сходится и имеет сумму S, то
(1) сходится и имеет сумму S, то 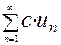 (2) тоже сходится, и имеет сумму CS, где С-const.
(2) тоже сходится, и имеет сумму CS, где С-const.
Доказательство: Пусть 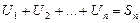 , n– ая частичная сумма 1 ряда.
, n– ая частичная сумма 1 ряда.
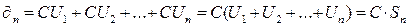 , n–ая частичная сумма 2 ряда.
, n–ая частичная сумма 2 ряда.
Т.к 1 ряд сходится, то 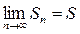 .
.
Рассмотрим 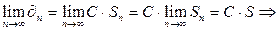 (2) ряд сходится.
(2) ряд сходится.
Конец доказательства.
2) Если 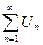 (1) сходится с суммой S1, и
(1) сходится с суммой S1, и 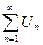 (2) сходится с суммой S2.
(2) сходится с суммой S2. 
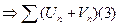 тоже сходится с суммой
тоже сходится с суммой 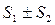 .
.
Доказательство:
Обозначим 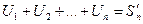 - n – частичная сумма 1 ряда.
- n – частичная сумма 1 ряда.
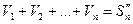 - n – частичная сумма 2 ряда.
- n – частичная сумма 2 ряда.
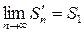
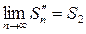
Рассмотрим n-ую частичную сумму ряда
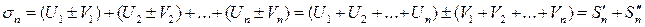
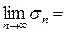
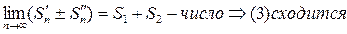 и сумма
и сумма 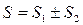 .
.
Конец доказательства.
3) Любой ряд может быть представлен в виде:
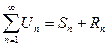 , где
, где 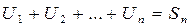 - n – частичная сумма
- n – частичная сумма
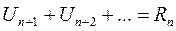 - n – остаток ряда.
- n – остаток ряда.
n – остаток ряда 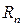 тоже является рядом.
тоже является рядом.
Если 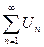 , то и его остаток
, то и его остаток 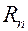 тоже сходится.
тоже сходится.
Доказательство: доказательство этого факта следует из того, что сумма ряда и сумма его остатка отличаются друг от друга на конечное число cлагаемых.
Конец доказательства.
Следствие: на сходимость ряда не влияет отбрасывание или приписывание в начало ряда конечного числа членов, например: 1+3+9+27+…
Дописывание: 1/9+1/3+1+3+9+27+.. отбрасывание: 1+3+5+7+9+11
4) Если 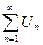 сходится с суммой S
сходится с суммой S 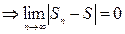 .
.
Общий вывод: на практике необязательно выяснять сходимость ряда по определению (вычисляя сумму S). Достаточно просто знать сходится этот ряд или расходится, поэтому, основное место в теории рядов занимают теоремы – признаки сходимости, которые позволяют исследовать ряд на сходимость, не вычисляя его суммы.
Признаки сходимости
Необходимый признак сходимости:
Если 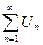 сходится, то общий член
сходится, то общий член 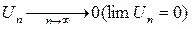
Доказательство: Пусть 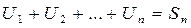 - n – частичная сумма.
- n – частичная сумма.
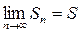 - число.
- число.
При 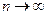 ,
, 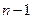 тоже
тоже 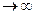 и
и 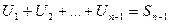 - n-1 – частичная сумма.
- n-1 – частичная сумма.
Она имеет предел 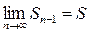 .
.
Т.к 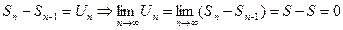
 конец доказательства.
конец доказательства.
Необходимый признак сходимости неудобен на практике, т.к по поведению общего члена Un на бесконечности нельзя судить о сходимости ряда.
На практике удобно пользоваться достаточным признаком расходимости ряда:
Если 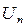 не стремится к 0 при
не стремится к 0 при 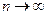
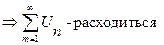
Примеры:
1) 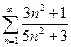
2) 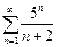
Радикальный признак Коши.
Дан ряд с положительными членами 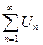 и
и 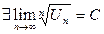
Если 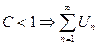 - сходиться
- сходиться
Если 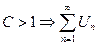 - расходиться
- расходиться
Если  - вопрос о сходимости не решен
- вопрос о сходимости не решен
Доказательство:
по определению 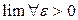
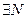 , начиная с которого
, начиная с которого 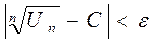
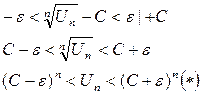
1) Пусть С<1 выберем 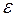 настолько малым, чтобы
настолько малым, чтобы  , тогда из правой части
, тогда из правой части 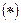
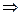
 <
< 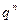 , ряд
, ряд 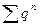 , где q<1 сходится как ряд из членов геометрической прогрессии, со знаменателем <1, тогда исходный ряд сходится по I признаку сравнения, т.к его члены меньше членов сходящегося ряда.
, где q<1 сходится как ряд из членов геометрической прогрессии, со знаменателем <1, тогда исходный ряд сходится по I признаку сравнения, т.к его члены меньше членов сходящегося ряда.
2) Пусть С>1 выберем 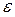 настолько малым, чтобы
настолько малым, чтобы 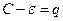 >1
>1 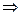 из левой части
из левой части 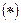
 >
> 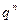 ;
; 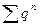 (q>1) расходится, как ряд из членов геометрической прогрессии, расходится по I признаку сравнения, т.к его члены больше членов сходящегося ряда.
(q>1) расходится, как ряд из членов геометрической прогрессии, расходится по I признаку сравнения, т.к его члены больше членов сходящегося ряда.
3)С=1
Возьмем 2 обобщенно гармонических ряда 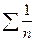 – расходится (p=1) и
– расходится (p=1) и 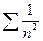 -сходится (p=2>1) и покажем, что С=1.
-сходится (p=2>1) и покажем, что С=1.
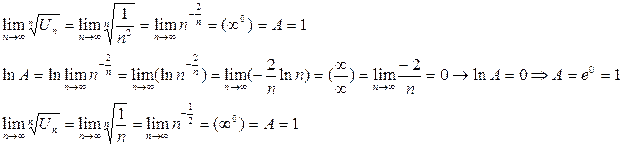

Таким образом при С=1 ряд может как сходится так и расходится.
Конец доказательства.
Примеры:
1) 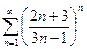
2) 
3) 
Интегральный признак Коши.
Дан ряд с положительными членами 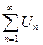 , что
, что 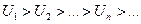 (
(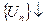 ) и функция f(x) – положительная и убывающая, связанная с рядом равенством f(n)=
) и функция f(x) – положительная и убывающая, связанная с рядом равенством f(n)=  . Тогда несобственный интеграл
. Тогда несобственный интеграл 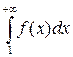 и
и 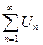 сходится и расходится одновременно.
сходится и расходится одновременно.
Доказательство:
f(n)=Un
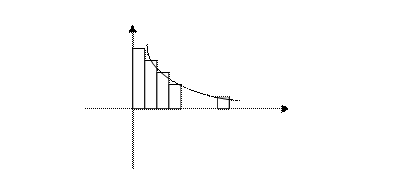
n
S ступенчатой фигуры над рядом (f(x))
 - n частичная сумма ряда.
- n частичная сумма ряда.
S ступенчатой фигуры под графиком функции f(x)
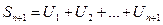 - n+1 частичная сумма ряда.
- n+1 частичная сумма ряда.
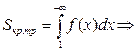 очевидно неравенство
очевидно неравенство 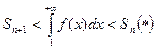
Пусть несобственный интеграл  сходится
сходится 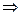

Из левой части 
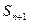 <числа
<числа 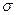
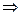
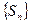 - ограничена сверху числом
- ограничена сверху числом 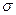
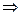
 - сходится.
- сходится.
Пусть 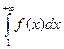 расходится
расходится 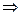
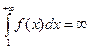
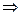 из правой части (*)
из правой части (*) 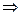
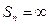
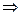
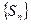 неограничен
неограничен 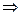 ряд расходится.
ряд расходится.
Конец доказательства.
Докажем, с помощью интегрального признака Коши, что обобщенно-гармонический ряд:
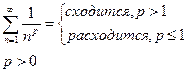
свяжем с эти рядом несобственный интеграл
 (доказано в несобственном интеграле)
(доказано в несобственном интеграле) 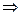 исходный несобственный интеграл сходится или расходится одновременно.
исходный несобственный интеграл сходится или расходится одновременно.
Примеры:
1) 
2) 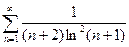
Конспект лекций по
Числовым рядам
Числовые ряды
Определение: Рассмотрим бесконечную числовую последовательность:
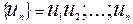 числовым рядом называется выражение
числовым рядом называется выражение 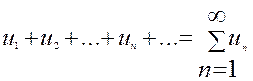 , где
, где 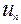 – общий член ряда.
– общий член ряда.
Пример:
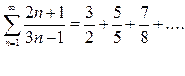 -знакоположительный ряд
-знакоположительный ряд
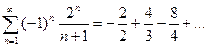 -знакочередующийся ряд
-знакочередующийся ряд
Последовательность 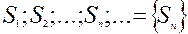 , где
, где 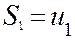 ;
; 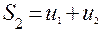 ;
; 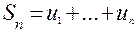 - последовательность частичных сумм ряда.
- последовательность частичных сумм ряда.
Каждая частичная сумма содержит конечное число слагаемых.
Числовой ряд 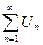 называется сходящимся, если существует конечный
называется сходящимся, если существует конечный
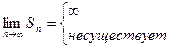 , то ряд называется расходящимся и суммы S не имеют.
, то ряд называется расходящимся и суммы S не имеют.
1)Рассмотрим ряд из членов геометрической прогрессии.
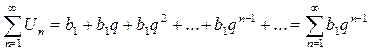 , где n – частичная сумма ряда
, где n – частичная сумма ряда 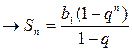 - сумма n первых членов геометрической прогрессии.
- сумма n первых членов геометрической прогрессии.
Рассмотрим 3 случая:
1) 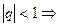 геометрическая прогрессия убывающая.
геометрическая прогрессия убывающая.
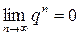
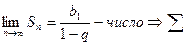 сходится и имеет сумму
сходится и имеет сумму 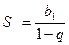
2) 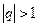
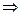
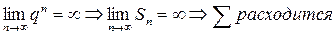
3) 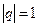
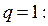
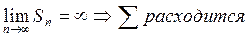
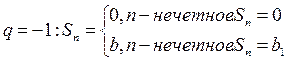
 = не существует – ряд расходится.
= не существует – ряд расходится.
Вывод: ряд из членов геометрической прогрессии сходится если 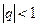 и расходится
и расходится 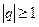

Элементарные свойства рядов
1) Если 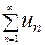 (1) сходится и имеет сумму S, то
(1) сходится и имеет сумму S, то 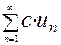 (2) тоже сходится, и имеет сумму CS, где С-const.
(2) тоже сходится, и имеет сумму CS, где С-const.
Доказательство: Пусть 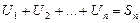 , n– ая частичная сумма 1 ряда.
, n– ая частичная сумма 1 ряда.
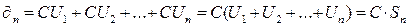 , n–ая частичная сумма 2 ряда.
, n–ая частичная сумма 2 ряда.
Т.к 1 ряд сходится, то 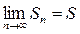 .
.
Рассмотрим 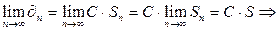 (2) ряд сходится.
(2) ряд сходится.
Конец доказательства.
2) Если 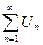 (1) сходится с суммой S1, и
(1) сходится с суммой S1, и 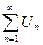 (2) сходится с суммой S2.
(2) сходится с суммой S2. 
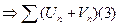 тоже сходится с суммой
тоже сходится с суммой 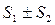 .
.
Доказательство:
Обозначим 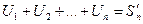 - n – частичная сумма 1 ряда.
- n – частичная сумма 1 ряда.
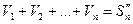 - n – частичная сумма 2 ряда.
- n – частичная сумма 2 ряда.
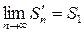
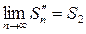
Рассмотрим n-ую частичную сумму ряда
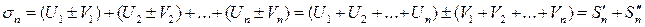
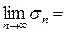
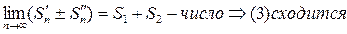 и сумма
и сумма 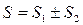 .
.
Конец доказательства.
3) Любой ряд может быть представлен в виде:
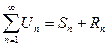 , где
, где 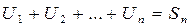 - n – частичная сумма
- n – частичная сумма
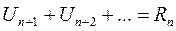 - n – остаток ряда.
- n – остаток ряда.
n – остаток ряда 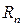 тоже является рядом.
тоже является рядом.
Если 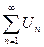 , то и его остаток
, то и его остаток 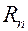 тоже сходится.
тоже сходится.
Доказательство: доказательство этого факта следует из того, что сумма ряда и сумма его остатка отличаются друг от друга на конечное число cлагаемых.
Конец доказательства.
Следствие: на сходимость ряда не влияет отбрасывание или приписывание в начало ряда конечного числа членов, например: 1+3+9+27+…
Дописывание: 1/9+1/3+1+3+9+27+.. отбрасывание: 1+3+5+7+9+11
4) Если 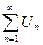 сходится с суммой S
сходится с суммой S 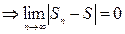 .
.
Общий вывод: на практике необязательно выяснять сходимость ряда по определению (вычисляя сумму S). Достаточно просто знать сходится этот ряд или расходится, поэтому, основное место в теории рядов занимают теоремы – признаки сходимости, которые позволяют исследовать ряд на сходимость, не вычисляя его суммы.
Признаки сходимости
Необходимый признак сходимости:
Если 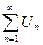 сходится, то общий член
сходится, то общий член 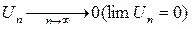
Доказательство: Пусть 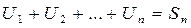 - n – частичная сумма.
- n – частичная сумма.
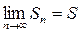 - число.
- число.
При 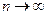 ,
, 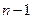 тоже
тоже 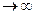 и
и 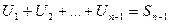 - n-1 – частичная сумма.
- n-1 – частичная сумма.
Она имеет предел 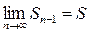 .
.
Т.к 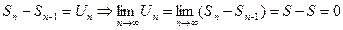
 конец доказательства.
конец доказательства.
Необходимый признак сходимости неудобен на практике, т.к по поведению общего члена Un на бесконечности нельзя судить о сходимости ряда.
На практике удобно пользоваться достаточным признаком расходимости ряда:
Если 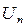 не стремится к 0 при
не стремится к 0 при 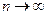
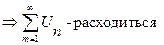
Примеры:
1) 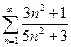
2) 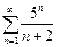
Числовые ряды с положительными членами
Рассмотрим знакоположительный числовой ряд 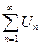 , где
, где 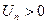 .Последовательность частичных сумм такого ряда будет всегда возрастающей:
.Последовательность частичных сумм такого ряда будет всегда возрастающей:
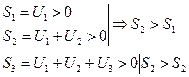
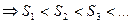
На 1 курсе была доказана теорема о том, что: монотонно возрастающая последовательность, ограниченная сверху имеет конечный предел.
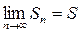 - число.
- число.
Для знакоположительного ряда достаточно доказать, что, последовательность частичных сумм 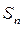 ограничена сверху числом (возрастание и так есть).
ограничена сверху числом (возрастание и так есть).
1й признак сравнения
Дано 2 ряда с положительными членами 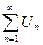 (1) и
(1) и 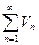 (2) и начиная с некоторого номера N выполняется неравенство
(2) и начиная с некоторого номера N выполняется неравенство 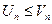 , тогда если (2) сходится то и (1) сходится. Если (1) расходится то и (2) тоже расходится, (ряд меньший сходящегося тоже сходится, ряд больший расходящегося тоже расходится).
, тогда если (2) сходится то и (1) сходится. Если (1) расходится то и (2) тоже расходится, (ряд меньший сходящегося тоже сходится, ряд больший расходящегося тоже расходится).
Доказательство: Обозначим через 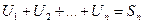 - n – частичная сумма 1 ряда и
- n – частичная сумма 1 ряда и  - n – частичная сумма 2 ряда.
- n – частичная сумма 2 ряда.
Т.к 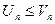
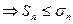 . Пусть 2 ряд сходится, тогда
. Пусть 2 ряд сходится, тогда 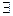
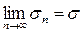 , причём
, причём 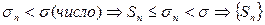 ограничена сверху числом
ограничена сверху числом 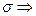 (1) сходится.
(1) сходится.
Пусть 1 ряд расходится 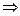
 , т.к
, т.к 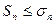
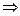
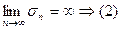 расходится.
расходится.
Конец доказательство.
Замечание: при доказательстве этого признака мы считали, что неравенство 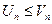 выполняется с 1 номера. Этот факт не влияет на сходимость, т.к по свойству рядов отбрасывание n – первых членов ряда на сходимость ряда не влияет.
выполняется с 1 номера. Этот факт не влияет на сходимость, т.к по свойству рядов отбрасывание n – первых членов ряда на сходимость ряда не влияет.
Для сравнения необходим стандартный набор рядов, о сходимости всё известно. К таким рядам относятся:
| Ряды для сравнения: | |
Ряды членов геометрической прогрессии:
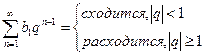
| Обобщенно гармонический ряд:
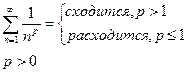 (строгое доказательство будет проведено после интегрального признака сходимости)
(строгое доказательство будет проведено после интегрального признака сходимости)
|
Примеры:
1) 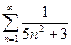
2) 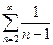
3) 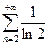

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!