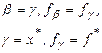Заметим, что точка  (n- тая итерация) отстоит от концов отрезка
(n- тая итерация) отстоит от концов отрезка 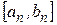 на величину, не превышающую
на величину, не превышающую 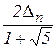 . Поэтому верна оценка:
. Поэтому верна оценка:
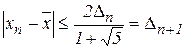 . (8)
. (8)
Каждая итерация сокращает длину отрезка локализации в 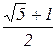 раз. Значит,
раз. Значит, 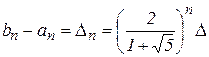 и справедлива следующая априорная оценка погрешности:
и справедлива следующая априорная оценка погрешности:
 . (9)
. (9)
Таким образом, метод золотого сечения сходится со скоростью геометрической прогрессии, знаменатель которой  .
.
2.4. Метод Фибоначчи *
Данный метод обеспечивает максимальное гарантированное сокращение отрезка локализации при заданном числе N вычислений функции и основан на использовании чисел Фибоначчи 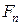 таких, что:
таких, что:  для всех
для всех 
при начальных значениях 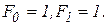
Метод Фибоначчи состоит из 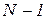 шагов. Очередной
шагов. Очередной  -й шаг выполняется аналогично
-й шаг выполняется аналогично  -й итерации метода деления отрезка пополам, но точки
-й итерации метода деления отрезка пополам, но точки 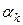 и
и 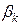 находятся по формулам
находятся по формулам
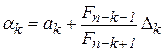 ,
, 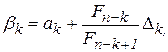 (10)
(10)
где 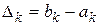 – длина отрезка локализации
– длина отрезка локализации 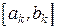 (рис.2.7).
(рис.2.7).
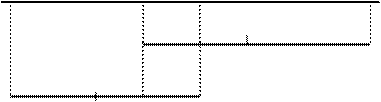
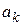
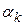
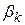
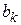
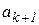
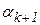
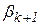
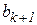
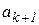
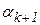
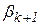
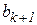
Рис. 2.7. Графическая интерпретация метода Фибоначчи
Аналогично методу деления отрезка пополам определяется новый отрезок локализации:
если 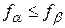 , то
, то 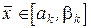 ;
;
если 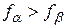 , то
, то 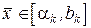 .
.
В первом случае за очередное приближение к точке минимума  принимают
принимают  , во втором случае –
, во втором случае – 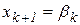 .
.
Оценка погрешности метода Фибоначчи
Так же, как и в методе золотого сечения точка  будет однозначно совпадать с одной из точек (в зависимости от выбора подотрезка на очередном шаге локализации):
будет однозначно совпадать с одной из точек (в зависимости от выбора подотрезка на очередном шаге локализации):

 ,
, 
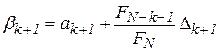 . (11)
. (11)
Поэтому на очередном шаге достаточно вычислить значение функции лишь в одной недостающей точке. В результате выполнения 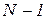 шагов отрезок локализации уменьшается в
шагов отрезок локализации уменьшается в 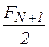 раз, а точка
раз, а точка  оказывается центральной для последнего отрезка локализации
оказывается центральной для последнего отрезка локализации 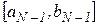 . Поэтому для
. Поэтому для 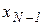 справедлива следующая оценка погрешности:
справедлива следующая оценка погрешности:
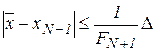
 . (12)
. (12)
Метод парабол
Существует множество методов локализации экстремума гладкой функции. Некоторые из них, например метод бисекции и метод Ньютона требуют вычисления производных. Такие методы достаточно эффективны, но не очень удобны для программной реализации, так как именно проблема вычисления производных является трудоемкой в ЭВМ-реализации. Предлагаемый метод не требует вычисления производных и, как мы убедимся ниже, является достаточно эффективным в случае удачной предварительной его настройки.
Предположим, что уже известны три предыдущих приближения к точке  – локального минимума функции
– локального минимума функции 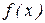 , т.е. получена локализующая тройка
, т.е. получена локализующая тройка  В качестве такой тройки можно воспользоваться, например, вычислениями, полученными на трех последних шагах (
В качестве такой тройки можно воспользоваться, например, вычислениями, полученными на трех последних шагах (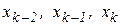 ) методом пассивного поиска. При этом соответствие между
) методом пассивного поиска. При этом соответствие между  и
и 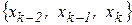 нужно установить так, чтобы выполнялось условие критерия 2:
нужно установить так, чтобы выполнялось условие критерия 2: 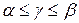 . Вложенная в
. Вложенная в 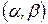 новая локализующая тройка строится при помощи интерполяционного полинома Ньютона
новая локализующая тройка строится при помощи интерполяционного полинома Ньютона 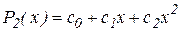 . График полинома
. График полинома 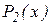 является параболой (рис.2.5.1), проходящей через три точки плоскости с координатами
является параболой (рис.2.5.1), проходящей через три точки плоскости с координатами  . Точка минимума
. Точка минимума  полинома
полинома 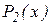 лежит в
лежит в  . Вычислив
. Вычислив 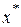 и
и 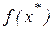 , сравним значение
, сравним значение 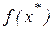 со значением
со значением 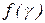 и по критерию 2 найдем новую локализирующую тройку.
и по критерию 2 найдем новую локализирующую тройку.
Полином 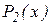 удобно представить в форме Ньютона с разделенными разностями:
удобно представить в форме Ньютона с разделенными разностями:
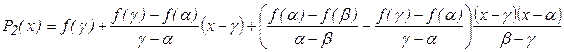 (13)
(13)
 y
y
y= 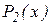
y= 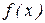
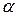
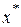
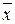
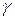
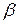 x
x
Рис.2.8. К методу парабол
В формуле (13) коэффициенты при неизвестных полинома 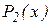 представлены формулами:
представлены формулами:
 ;
;
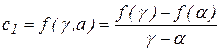 ;
;
 .
.
Сделав соответствующие приведения в терминах разделенных разностей, точку 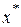 можно определить, воспользовавшись одной из формул:
можно определить, воспользовавшись одной из формул:
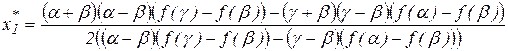 , (14)
, (14)
или
 , (15)
, (15)
или
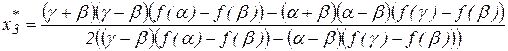 . (16)
. (16)
Выбор точки  следует сделать по тому представлению, которое будет вычисляться с меньшей потерей точности (значащих цифр в разностях). Однако, такой выбор на ЭВМ осуществить достаточно трудоемко. Поэтому, для определения конкретной точки
следует сделать по тому представлению, которое будет вычисляться с меньшей потерей точности (значащих цифр в разностях). Однако, такой выбор на ЭВМ осуществить достаточно трудоемко. Поэтому, для определения конкретной точки 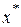 в ЭВМ-реализации можно принять условие: выбрать ту точку, значение которой по величине является средним из трех возможных. То есть:
в ЭВМ-реализации можно принять условие: выбрать ту точку, значение которой по величине является средним из трех возможных. То есть:
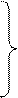
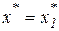 , если
, если 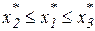 , или
, или 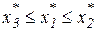 ;
;
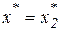 , если
, если 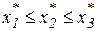 , или
, или 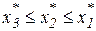 ; (17)
; (17)
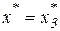 , если
, если 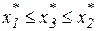 , или
, или 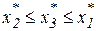 .
.
Кроме того, и это существенно, на выбор точки 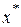 влияет также то, насколько близко точка
влияет также то, насколько близко точка 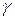 оказывается к точкам
оказывается к точкам 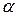 и
и 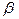 на числовой оси.
на числовой оси.
Если
а) 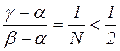 ,
,
или
б)  ,
,
то большое значение N в этих отношениях ( ) означает одностороннюю сходимость к стационарной точке, но не к точке локального минимума. Поэтому, при выполнении условия а) следует положить
) означает одностороннюю сходимость к стационарной точке, но не к точке локального минимума. Поэтому, при выполнении условия а) следует положить 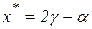 , а при выполнении условия б) принять точку
, а при выполнении условия б) принять точку 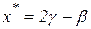 .
.
Начало
1
Ввод 
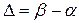

 Конец
Конец
проверка нет выбор
условий новой нет
критерия 2 тройки
да 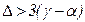
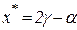
вычисление 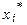
по (14)-(16) и
выбор по (17) 
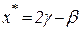
нет
14
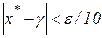
да
2 

да
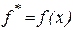
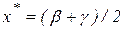
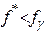
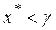
 2
2
да да
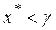
да
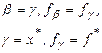

1
Схема 2.5. К методу парабол
* Леонардо Пизанский (1180-1240)–итальянский математик.



 (n- тая итерация) отстоит от концов отрезка
(n- тая итерация) отстоит от концов отрезка 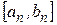 на величину, не превышающую
на величину, не превышающую 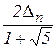 . Поэтому верна оценка:
. Поэтому верна оценка: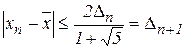 . (8)
. (8)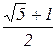 раз. Значит,
раз. Значит, 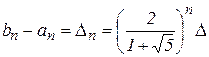 и справедлива следующая априорная оценка погрешности:
и справедлива следующая априорная оценка погрешности: . (9)
. (9) .
.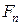 таких, что:
таких, что:  для всех
для всех 
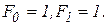
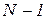 шагов. Очередной
шагов. Очередной  -й шаг выполняется аналогично
-й шаг выполняется аналогично 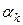 и
и 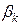 находятся по формулам
находятся по формулам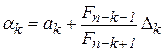 ,
, 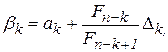 (10)
(10)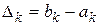 – длина отрезка локализации
– длина отрезка локализации 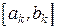 (рис.2.7).
(рис.2.7).
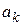
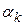
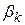
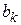
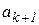
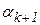
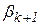
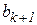
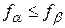 , то
, то 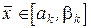 ;
;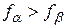 , то
, то 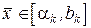 .
. принимают
принимают  , во втором случае –
, во втором случае – 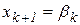 .
. будет однозначно совпадать с одной из точек (в зависимости от выбора подотрезка на очередном шаге локализации):
будет однозначно совпадать с одной из точек (в зависимости от выбора подотрезка на очередном шаге локализации):
 ,
, 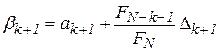 . (11)
. (11)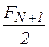 раз, а точка
раз, а точка  оказывается центральной для последнего отрезка локализации
оказывается центральной для последнего отрезка локализации 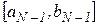 . Поэтому для
. Поэтому для 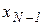 справедлива следующая оценка погрешности:
справедлива следующая оценка погрешности: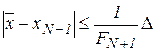
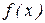 , т.е. получена локализующая тройка
, т.е. получена локализующая тройка  В качестве такой тройки можно воспользоваться, например, вычислениями, полученными на трех последних шагах (
В качестве такой тройки можно воспользоваться, например, вычислениями, полученными на трех последних шагах (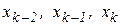 ) методом пассивного поиска. При этом соответствие между
) методом пассивного поиска. При этом соответствие между 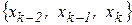 нужно установить так, чтобы выполнялось условие критерия 2:
нужно установить так, чтобы выполнялось условие критерия 2: 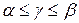 . Вложенная в
. Вложенная в 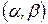 новая локализующая тройка строится при помощи интерполяционного полинома Ньютона
новая локализующая тройка строится при помощи интерполяционного полинома Ньютона 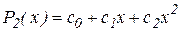 . График полинома
. График полинома 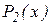 является параболой (рис.2.5.1), проходящей через три точки плоскости с координатами
является параболой (рис.2.5.1), проходящей через три точки плоскости с координатами  . Точка минимума
. Точка минимума  полинома
полинома  . Вычислив
. Вычислив 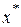 и
и 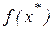 , сравним значение
, сравним значение 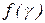 и по критерию 2 найдем новую локализирующую тройку.
и по критерию 2 найдем новую локализирующую тройку.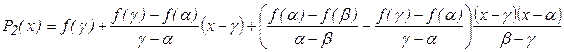 (13)
(13) y
y
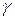
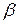 x
x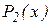 представлены формулами:
представлены формулами: ;
;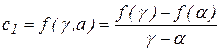 ;
; .
.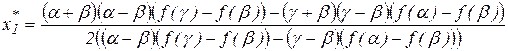 , (14)
, (14) , (15)
, (15)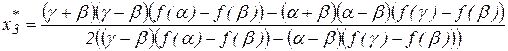 . (16)
. (16) следует сделать по тому представлению, которое будет вычисляться с меньшей потерей точности (значащих цифр в разностях). Однако, такой выбор на ЭВМ осуществить достаточно трудоемко. Поэтому, для определения конкретной точки
следует сделать по тому представлению, которое будет вычисляться с меньшей потерей точности (значащих цифр в разностях). Однако, такой выбор на ЭВМ осуществить достаточно трудоемко. Поэтому, для определения конкретной точки 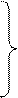
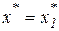 , если
, если 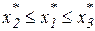 , или
, или 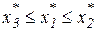 ;
;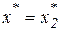 , если
, если 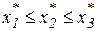 , или
, или 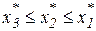 ; (17)
; (17)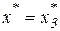 , если
, если 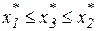 , или
, или 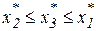 .
.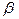 на числовой оси.
на числовой оси.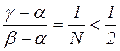 ,
, ,
, ) означает одностороннюю сходимость к стационарной точке, но не к точке локального минимума. Поэтому, при выполнении условия а) следует положить
) означает одностороннюю сходимость к стационарной точке, но не к точке локального минимума. Поэтому, при выполнении условия а) следует положить 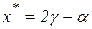 , а при выполнении условия б) принять точку
, а при выполнении условия б) принять точку 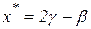 .
.

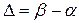

 Конец
Конец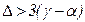
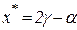
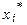

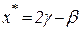
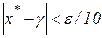


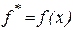
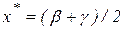
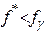
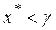
 2
2