Проверка гипотезы о значении генеральной дисперсии
Пусть из генеральной совокупности, значения признака которой распределены по нормальному закону с неизвестной дисперсией 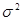 взята случайная выборка из n независимых наблюдений и пусть S2 — выборочная дисперсия.
взята случайная выборка из n независимых наблюдений и пусть S2 — выборочная дисперсия.
Требуется проверить нулевую гипотезу  , где
, где 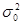 — определенное заданное значение дисперсии.
— определенное заданное значение дисперсии.
Для проверки нулевой гипотезы используют выборочную характеристику (2.30):
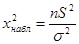 ,
,
которая при выполнении гипотезы 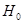 имеет распределение
имеет распределение 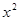 с n-1 степенями свободы.
с n-1 степенями свободы.
Как и выше, в зависимости от конкурирующей гипотезы выбирают правостороннюю, левостороннюю или двустороннюю критические области. Границы критической области 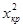 определяют по таблице распределения
определяют по таблице распределения 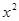 для заданного уровня значимости
для заданного уровня значимости  и числа степеней свободы n-1. Рассмотрим три случая.
и числа степеней свободы n-1. Рассмотрим три случая.
1. Если 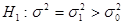 , то выбирают правостороннюю критическую область и
, то выбирают правостороннюю критическую область и  находят из условия:
находят из условия:
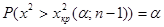 , (2.52)
, (2.52)
где  – табличное значение
– табличное значение 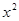 , найденное для уровня значимости
, найденное для уровня значимости 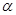 и числа степеней свободы n-1.
и числа степеней свободы n-1.
Правило проверки гипотезы следующее: если 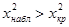 , то нулевую гипотезу
, то нулевую гипотезу 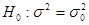 отвергают, если
отвергают, если 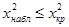 , то нулевая гипотеза не противоречит опытным данным.
, то нулевая гипотеза не противоречит опытным данным.
Для вычисления мощности критерия можно воспользоваться формулой:
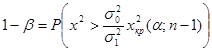 . (2.53)
. (2.53)
2. Если конкурирующая гипотеза  , то строят двустороннюю критическую область. Левую (
, то строят двустороннюю критическую область. Левую (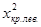 ) и правую (
) и правую (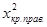 ) границы критической области находят из условия:
) границы критической области находят из условия:
 ;
; 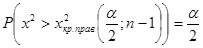 (2.54)
(2.54)
В этом случае правило проверки гипотезы сводится к следующему: если 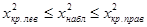 , то у нас нет основания отвергнуть гипотезу. Если же
, то у нас нет основания отвергнуть гипотезу. Если же 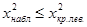 или
или 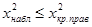 , то гипотезу отвергают.
, то гипотезу отвергают.
3. При конкурирующей гипотезе 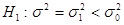 строят левостороннюю критическую область. Границу критической области определяют по таблице распределения
строят левостороннюю критическую область. Границу критической области определяют по таблице распределения 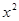 (таблица 3 Приложения) – из условия:
(таблица 3 Приложения) – из условия:
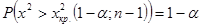 . (2.55)
. (2.55)
Если 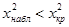 , то гипотеза
, то гипотеза 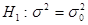 отвергается, если же
отвергается, если же 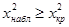 , то гипотеза не отвергается.
, то гипотеза не отвергается.
Для вычисления мощности критерия можно воспользоваться формулой:
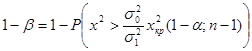 . (2.56)
. (2.56)
Пример 10.3. По результатам n=18 независимых измерений найдено, что 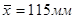 , а S=0,5мм. Допустив, что ошибки измерения имеют нормальное распределение:
, а S=0,5мм. Допустив, что ошибки измерения имеют нормальное распределение:
а) проверить на уровне значимости 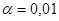 гипотезу
гипотезу 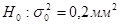 против конкурирующей гипотезы
против конкурирующей гипотезы 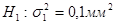 и вычислить мощность критерия;
и вычислить мощность критерия;
б) проверить на уровне значимости  гипотезу
гипотезу 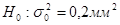 против конкурирующей гипотезы
против конкурирующей гипотезы 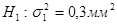 и вычислить мощность критерия;
и вычислить мощность критерия;
в) проверить на уровне значимости 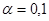 гипотезу
гипотезу  против конкурирующей гипотезы
против конкурирующей гипотезы 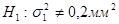 .
.
Решение.
А. В основе проверки гипотезы о значении генеральной дисперсии лежит статистика  , наблюдаемое значение которой равно:
, наблюдаемое значение которой равно:
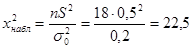 .
.
Так как альтернативная гипотеза 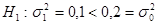 , то гипотеза
, то гипотеза 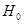 отклоняется в пользу гипотезы
отклоняется в пользу гипотезы 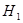 при попадании статистики критерия в левостороннюю критическую область, границы которой определяются из условия (2.55):
при попадании статистики критерия в левостороннюю критическую область, границы которой определяются из условия (2.55):
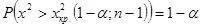 .
.
По таблицам распределения, 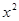 (таблица 3 Приложения):
(таблица 3 Приложения):
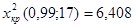 .
.
Вывод. Поскольку наблюдаемое значение статистики критерия не меньше критического значения  , то можно сделать вывод, что на уровне значимости
, то можно сделать вывод, что на уровне значимости 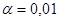 гипотеза
гипотеза 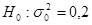 не противоречит опытным данным.
не противоречит опытным данным.
Мощность критерия проверки гипотезы о значении генеральной дисперсии в случае левосторонней критической области определяется по формуле (2.56):

Б. Наблюдаемое значение статистики:
 .
.
Так как альтернативная гипотеза 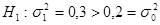 , то гипотеза
, то гипотеза 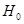 отклоняется в пользу гипотезы
отклоняется в пользу гипотезы 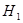 при попадании статистики критерия в левостороннюю критическую область, границы которой определяются из условия (2.55):
при попадании статистики критерия в левостороннюю критическую область, границы которой определяются из условия (2.55):
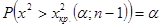 .
.
По таблицам распределения, 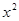 :
:
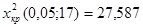 .
.
Вывод. Так как наблюдаемое значение статистики критерия не превосходит критическое значение 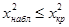 , то можно сделать вывод, что на уровне значимости
, то можно сделать вывод, что на уровне значимости 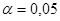 гипотеза
гипотеза 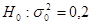 не противоречит опытным данным.
не противоречит опытным данным.
Мощность критерия проверки гипотезы о значении генеральной дисперсии в случае правосторонней критической области определяется по формуле (2.56):
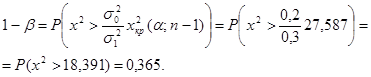
В. Наблюдаемое значение статистики:
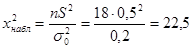 .
.
Так как альтернативная гипотеза  , то гипотеза
, то гипотеза  отклоняется в пользу гипотезы
отклоняется в пользу гипотезы 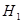 при попадании статистики критерия в левостороннюю критическую область, границы которой определяются из условия (2.55):
при попадании статистики критерия в левостороннюю критическую область, границы которой определяются из условия (2.55):
 ;
;  .
.
По таблицам распределения, 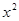 :
:
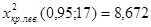 ;
;  .
.
Вывод. Так как наблюдаемое значение статистики критерия 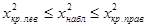 , то можно сделать вывод, что на уровне значимости
, то можно сделать вывод, что на уровне значимости 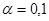 гипотеза
гипотеза 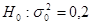 не противоречит опытным данным.
не противоречит опытным данным.
Проверка гипотезы о равенстве дисперсий двух генеральных совокупностей
Пусть Х и Y— генеральные совокупности, значения признаков которых распределены по нормальному закону с дисперсиями 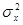 и
и 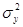 . Из этих совокупностей взяты независимые случайные выборки объемом
. Из этих совокупностей взяты независимые случайные выборки объемом 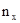 и
и 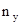 , и пусть
, и пусть 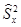 и
и 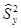 — исправленные выборочные дисперсии, причем
— исправленные выборочные дисперсии, причем
 , где
, где 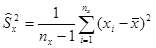 ,
,  .
.
Требуется проверить нулевую гипотезу 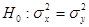 против альтернативной гипотезы
против альтернативной гипотезы 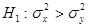 . Основу критерия для проверки нулевой гипотезы составляет статистика (2.33):
. Основу критерия для проверки нулевой гипотезы составляет статистика (2.33):
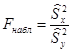 , (2.57)
, (2.57)
которая при выполнении нулевой гипотезы имеет распределение Фишера-Снедекора (F-распределение) с  и
и  степенями свободы.
степенями свободы.
Для поверки гипотезы выбирают правостороннюю критическую область. Границу критической области 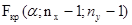 определяют по таблице F-распределения при заданном уровне значимости
определяют по таблице F-распределения при заданном уровне значимости  и числе степеней свободы
и числе степеней свободы 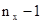 и
и 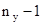 из условия:
из условия:
 . (2.58)
. (2.58)
Критерий проверки гипотезы состоит в том, что при выполнении условия 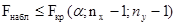 , полагают, что гипотеза не противоречит опытным данным; а если
, полагают, что гипотеза не противоречит опытным данным; а если  , то гипотезу отвергают.
, то гипотезу отвергают.
Пример 10.4. Для исследования состава работников предприятий были сделаны выборки по 10 предприятиям (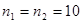 ) и определена доля мужчин в общей численности работников в каждой выборке. Для предприятий первой отрасли средняя доля составила
) и определена доля мужчин в общей численности работников в каждой выборке. Для предприятий первой отрасли средняя доля составила 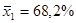 со стандартным отклонением
со стандартным отклонением 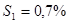 , для предприятий второй отрасли средняя доля составила
, для предприятий второй отрасли средняя доля составила 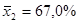 со стандартным отклонением
со стандартным отклонением 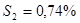 . Имеются ли основания полагать, что состав работников различается в этих двух отраслях?
. Имеются ли основания полагать, что состав работников различается в этих двух отраслях?
Решение.
Прежде чем приступить к проверке требуемой гипотезы о равенстве генеральных средних 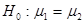 необходимо отметить, что в основе проверки гипотезы о равенстве генеральных средних лежит условие, что истинные значения генеральных дисперсий не известны, но равны:
необходимо отметить, что в основе проверки гипотезы о равенстве генеральных средних лежит условие, что истинные значения генеральных дисперсий не известны, но равны: 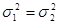 , и проверка гипотезы о равенстве генеральных средних без предварительной проверки гипотезы о равенстве генеральных дисперсий двух совокупностей не корректна.
, и проверка гипотезы о равенстве генеральных средних без предварительной проверки гипотезы о равенстве генеральных дисперсий двух совокупностей не корректна.
Поэтому сначала проверим гипотезу о равенстве генеральных дисперсий двух совокупностей, т. е. проверим на уровне значимости 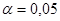 гипотезу
гипотезу 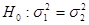 против конкурирующей гипотезы
против конкурирующей гипотезы  . В основе проверки гипотезы о значении генеральной дисперсии лежит статистика
. В основе проверки гипотезы о значении генеральной дисперсии лежит статистика 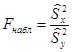 (в предположении, что
(в предположении, что  ), которая при выполнении нулевой гипотезы имеет распределение Фишера-Снедекора (F-распределение) с
), которая при выполнении нулевой гипотезы имеет распределение Фишера-Снедекора (F-распределение) с 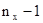 и
и 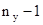 степенями свободы. Рассчитаем:
степенями свободы. Рассчитаем:
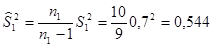 ;
;
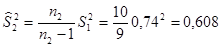 .
.
Так как 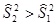 , то наблюдаемое значение статистики:
, то наблюдаемое значение статистики:
 .
.
Границы критической области определяются по таблицам распределения Фишера-Снедекора (таблица 4 Приложения) из условия 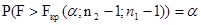 , откуда
, откуда 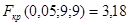 .
.
Вывод. Так как наблюдаемое значение статистики критерия меньше критического значения 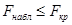 , то можно сделать вывод, что различия между дисперсиями двух совокупностей не существенны на 5%-м уровне значимости. Поэтому можно предположить, что две генеральные дисперсии равны друг другу и перейти к проверке гипотезы о равенстве генеральных средних, т. е. на уровне значимости
, то можно сделать вывод, что различия между дисперсиями двух совокупностей не существенны на 5%-м уровне значимости. Поэтому можно предположить, что две генеральные дисперсии равны друг другу и перейти к проверке гипотезы о равенстве генеральных средних, т. е. на уровне значимости 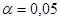 гипотезы
гипотезы 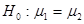 против конкурирующей гипотезы
против конкурирующей гипотезы 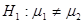 .
.
В основе проверки гипотезы о равенстве генеральных средних (в случае когда истинные значения генеральных дисперсий не известны, но  ) лежит статистика
) лежит статистика  , которая при выполнении нулевой гипотезы имеет распределение Стьюдента (t-распределение) с
, которая при выполнении нулевой гипотезы имеет распределение Стьюдента (t-распределение) с  степенями свободы.
степенями свободы.
Наблюдаемое значение статистики равно:
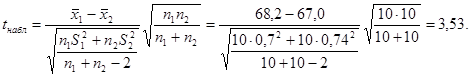
Так как альтернативная гипотеза  , то гипотеза
, то гипотеза 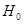 отклоняется в пользу гипотезы
отклоняется в пользу гипотезы  при попадании статистики критерия в двустороннюю критическую область, границы которой определяются из условия:
при попадании статистики критерия в двустороннюю критическую область, границы которой определяются из условия: 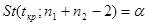 . По таблицам t-распределения:
. По таблицам t-распределения: 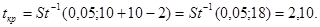
Вывод. Поскольку наблюдаемое значение статистики критерия по модулю превосходит критическое  , то можно сделать вывод, что наблюдения не согласуются с нулевой гипотезой, т. е. состав работников на предприятиях двух отраслей различен.
, то можно сделать вывод, что наблюдения не согласуются с нулевой гипотезой, т. е. состав работников на предприятиях двух отраслей различен.
Проверка гипотез об однородности ряда дисперсий
1. Критерий Бартлетта. Пусть  есть l нормальных генеральных совокупностей, из которых извлечены выборки объемом
есть l нормальных генеральных совокупностей, из которых извлечены выборки объемом 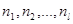 соответственно, и пусть
соответственно, и пусть 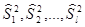 - исправленные выборочные дисперсии (2.13).
- исправленные выборочные дисперсии (2.13).
Требуется на уровне значимости  проверить нулевую гипотезу о равенстве дисперсий l генеральных совокупностей, т. е.
проверить нулевую гипотезу о равенстве дисперсий l генеральных совокупностей, т. е.  .
.
Введем обозначения:
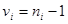 – число степеней свободы i-й выборки;
– число степеней свободы i-й выборки;
 для
для  , где
, где 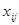 – результат j-го наблюдения i-й выборки;
– результат j-го наблюдения i-й выборки;
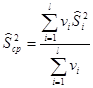 . (2.59)
. (2.59)
В качестве выборочной характеристики критерия Бартлетт предложил использовать статистику
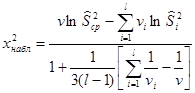 , (2.60)
, (2.60)
где 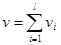 .
.
При выполнении нулевой гипотезы  и при
и при 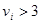 ,
,  приближенно имеет распределение
приближенно имеет распределение 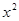 с l-1 степенями свободы.
с l-1 степенями свободы.
Для проверки нулевой гипотезы строят правостороннюю критическую область, границу которой определяют по таблице распределения 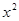 (таблица 3 Приложения) для уровня значимости
(таблица 3 Приложения) для уровня значимости 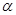 и числа степеней свободы l-1 из условия:
и числа степеней свободы l-1 из условия:
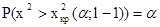 . (2.61)
. (2.61)
Критерий проверки гипотезы заключается в следующем: если 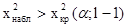 , то гипотезу отвергают, если же
, то гипотезу отвергают, если же 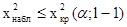 , то считают, что гипотеза не противоречит опытным данным.
, то считают, что гипотеза не противоречит опытным данным.
Критерий Бартлетта весьма чувствителен к отклонениям законов распределения 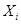 для
для 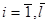 от нормального закона.
от нормального закона.
В случае, когда 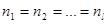 , для проверки нулевой гипотезы
, для проверки нулевой гипотезы 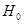 используют критерий Кохрана.
используют критерий Кохрана.
2. Критерий Кохрана. Пусть  – нормальные генеральные совокупности с неизвестными дисперсиями
– нормальные генеральные совокупности с неизвестными дисперсиями 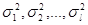 , из которых извлечены выборки объемом
, из которых извлечены выборки объемом 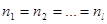 , и пусть
, и пусть 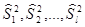 - исправленные выборочные дисперсии соответствующих совокупностей.
- исправленные выборочные дисперсии соответствующих совокупностей.
Требуется проверить нулевую гипотезу  . С целью проверки нулевой гипотезы Кохран предложил критерий, основанный на статистике:
. С целью проверки нулевой гипотезы Кохран предложил критерий, основанный на статистике:
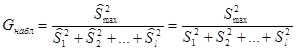 , (2.62)
, (2.62)
которая при выполнении нулевой гипотезы имеет G-распределение с 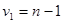 и
и 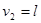 степенями свободы, где
степенями свободы, где 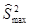 – наибольшая из исправленных выборочных дисперсий.
– наибольшая из исправленных выборочных дисперсий.
Для проверки нулевой гипотезы 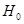 на уровне значимости
на уровне значимости  строят правостороннюю критическую область.
строят правостороннюю критическую область.
Границу критической области, 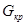 находят по таблице G-распределения (таблица 9 Приложения) из условия:
находят по таблице G-распределения (таблица 9 Приложения) из условия:
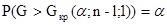 . (2.63)
. (2.63)
Критерий проверки гипотезы заключается в следующем: если выполняется условие 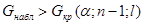 , то гипотезу отвергают, если же
, то гипотезу отвергают, если же 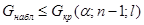 , то считают, что гипотеза не противоречит опытным данным.
, то считают, что гипотеза не противоречит опытным данным.



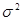 взята случайная выборка из n независимых наблюдений и пусть S2 — выборочная дисперсия.
взята случайная выборка из n независимых наблюдений и пусть S2 — выборочная дисперсия. , где
, где 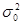 — определенное заданное значение дисперсии.
— определенное заданное значение дисперсии.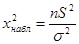 ,
,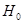 имеет распределение
имеет распределение 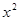 с n-1 степенями свободы.
с n-1 степенями свободы.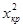 определяют по таблице распределения
определяют по таблице распределения 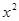 для заданного уровня значимости
для заданного уровня значимости  и числа степеней свободы n-1. Рассмотрим три случая.
и числа степеней свободы n-1. Рассмотрим три случая.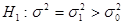 , то выбирают правостороннюю критическую область и
, то выбирают правостороннюю критическую область и  находят из условия:
находят из условия: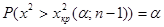 , (2.52)
, (2.52) – табличное значение
– табличное значение 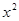 , найденное для уровня значимости
, найденное для уровня значимости 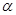 и числа степеней свободы n-1.
и числа степеней свободы n-1.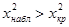 , то нулевую гипотезу
, то нулевую гипотезу 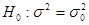 отвергают, если
отвергают, если 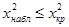 , то нулевая гипотеза не противоречит опытным данным.
, то нулевая гипотеза не противоречит опытным данным.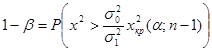 . (2.53)
. (2.53) , то строят двустороннюю критическую область. Левую (
, то строят двустороннюю критическую область. Левую (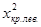 ) и правую (
) и правую (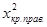 ) границы критической области находят из условия:
) границы критической области находят из условия: ;
; 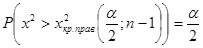 (2.54)
(2.54)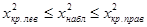 , то у нас нет основания отвергнуть гипотезу. Если же
, то у нас нет основания отвергнуть гипотезу. Если же 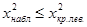 или
или 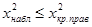 , то гипотезу отвергают.
, то гипотезу отвергают.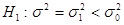 строят левостороннюю критическую область. Границу критической области определяют по таблице распределения
строят левостороннюю критическую область. Границу критической области определяют по таблице распределения 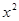 (таблица 3 Приложения) – из условия:
(таблица 3 Приложения) – из условия: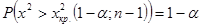 . (2.55)
. (2.55)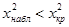 , то гипотеза
, то гипотеза 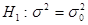 отвергается, если же
отвергается, если же 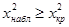 , то гипотеза не отвергается.
, то гипотеза не отвергается.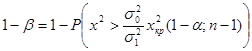 . (2.56)
. (2.56)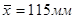 , а S=0,5мм. Допустив, что ошибки измерения имеют нормальное распределение:
, а S=0,5мм. Допустив, что ошибки измерения имеют нормальное распределение: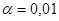 гипотезу
гипотезу 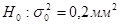 против конкурирующей гипотезы
против конкурирующей гипотезы 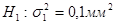 и вычислить мощность критерия;
и вычислить мощность критерия; гипотезу
гипотезу 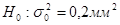 против конкурирующей гипотезы
против конкурирующей гипотезы 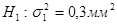 и вычислить мощность критерия;
и вычислить мощность критерия;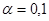 гипотезу
гипотезу  против конкурирующей гипотезы
против конкурирующей гипотезы 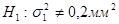 .
. , наблюдаемое значение которой равно:
, наблюдаемое значение которой равно: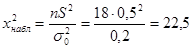 .
.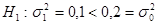 , то гипотеза
, то гипотеза 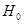 отклоняется в пользу гипотезы
отклоняется в пользу гипотезы 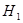 при попадании статистики критерия в левостороннюю критическую область, границы которой определяются из условия (2.55):
при попадании статистики критерия в левостороннюю критическую область, границы которой определяются из условия (2.55):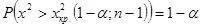 .
.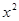 (таблица 3 Приложения):
(таблица 3 Приложения):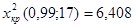 .
. , то можно сделать вывод, что на уровне значимости
, то можно сделать вывод, что на уровне значимости 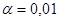 гипотеза
гипотеза 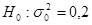 не противоречит опытным данным.
не противоречит опытным данным.
 .
.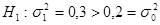 , то гипотеза
, то гипотеза 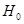 отклоняется в пользу гипотезы
отклоняется в пользу гипотезы 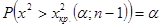 .
.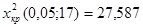 .
.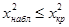 , то можно сделать вывод, что на уровне значимости
, то можно сделать вывод, что на уровне значимости 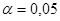 гипотеза
гипотеза 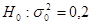 не противоречит опытным данным.
не противоречит опытным данным.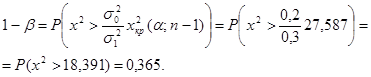
 , то гипотеза
, то гипотеза  отклоняется в пользу гипотезы
отклоняется в пользу гипотезы 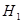 при попадании статистики критерия в левостороннюю критическую область, границы которой определяются из условия (2.55):
при попадании статистики критерия в левостороннюю критическую область, границы которой определяются из условия (2.55): ;
;  .
.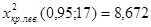 ;
;  .
.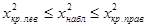 , то можно сделать вывод, что на уровне значимости
, то можно сделать вывод, что на уровне значимости 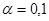 гипотеза
гипотеза 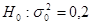 не противоречит опытным данным.
не противоречит опытным данным.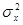 и
и 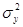 . Из этих совокупностей взяты независимые случайные выборки объемом
. Из этих совокупностей взяты независимые случайные выборки объемом 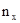 и
и 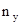 , и пусть
, и пусть 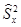 и
и 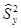 — исправленные выборочные дисперсии, причем
— исправленные выборочные дисперсии, причем , где
, где 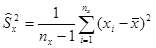 ,
,  .
.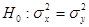 против альтернативной гипотезы
против альтернативной гипотезы 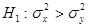 . Основу критерия для проверки нулевой гипотезы составляет статистика (2.33):
. Основу критерия для проверки нулевой гипотезы составляет статистика (2.33):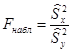 , (2.57)
, (2.57) и
и  степенями свободы.
степенями свободы.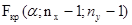 определяют по таблице F-распределения при заданном уровне значимости
определяют по таблице F-распределения при заданном уровне значимости  и числе степеней свободы
и числе степеней свободы 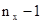 и
и 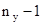 из условия:
из условия: . (2.58)
. (2.58)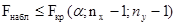 , полагают, что гипотеза не противоречит опытным данным; а если
, полагают, что гипотеза не противоречит опытным данным; а если  , то гипотезу отвергают.
, то гипотезу отвергают.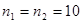 ) и определена доля мужчин в общей численности работников в каждой выборке. Для предприятий первой отрасли средняя доля составила
) и определена доля мужчин в общей численности работников в каждой выборке. Для предприятий первой отрасли средняя доля составила 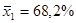 со стандартным отклонением
со стандартным отклонением 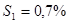 , для предприятий второй отрасли средняя доля составила
, для предприятий второй отрасли средняя доля составила 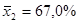 со стандартным отклонением
со стандартным отклонением 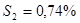 . Имеются ли основания полагать, что состав работников различается в этих двух отраслях?
. Имеются ли основания полагать, что состав работников различается в этих двух отраслях?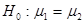 необходимо отметить, что в основе проверки гипотезы о равенстве генеральных средних лежит условие, что истинные значения генеральных дисперсий не известны, но равны:
необходимо отметить, что в основе проверки гипотезы о равенстве генеральных средних лежит условие, что истинные значения генеральных дисперсий не известны, но равны: 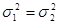 , и проверка гипотезы о равенстве генеральных средних без предварительной проверки гипотезы о равенстве генеральных дисперсий двух совокупностей не корректна.
, и проверка гипотезы о равенстве генеральных средних без предварительной проверки гипотезы о равенстве генеральных дисперсий двух совокупностей не корректна.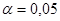 гипотезу
гипотезу 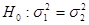 против конкурирующей гипотезы
против конкурирующей гипотезы  . В основе проверки гипотезы о значении генеральной дисперсии лежит статистика
. В основе проверки гипотезы о значении генеральной дисперсии лежит статистика 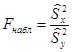 (в предположении, что
(в предположении, что  ), которая при выполнении нулевой гипотезы имеет распределение Фишера-Снедекора (F-распределение) с
), которая при выполнении нулевой гипотезы имеет распределение Фишера-Снедекора (F-распределение) с 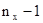 и
и 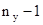 степенями свободы. Рассчитаем:
степенями свободы. Рассчитаем: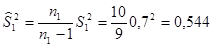 ;
;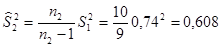 .
.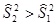 , то наблюдаемое значение статистики:
, то наблюдаемое значение статистики: .
.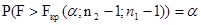 , откуда
, откуда 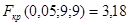 .
.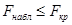 , то можно сделать вывод, что различия между дисперсиями двух совокупностей не существенны на 5%-м уровне значимости. Поэтому можно предположить, что две генеральные дисперсии равны друг другу и перейти к проверке гипотезы о равенстве генеральных средних, т. е. на уровне значимости
, то можно сделать вывод, что различия между дисперсиями двух совокупностей не существенны на 5%-м уровне значимости. Поэтому можно предположить, что две генеральные дисперсии равны друг другу и перейти к проверке гипотезы о равенстве генеральных средних, т. е. на уровне значимости 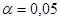 гипотезы
гипотезы 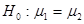 против конкурирующей гипотезы
против конкурирующей гипотезы 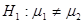 .
. ) лежит статистика
) лежит статистика  , которая при выполнении нулевой гипотезы имеет распределение Стьюдента (t-распределение) с
, которая при выполнении нулевой гипотезы имеет распределение Стьюдента (t-распределение) с  степенями свободы.
степенями свободы.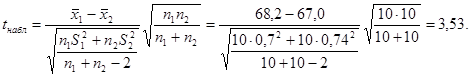
 , то гипотеза
, то гипотеза 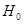 отклоняется в пользу гипотезы
отклоняется в пользу гипотезы  при попадании статистики критерия в двустороннюю критическую область, границы которой определяются из условия:
при попадании статистики критерия в двустороннюю критическую область, границы которой определяются из условия: 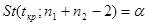 . По таблицам t-распределения:
. По таблицам t-распределения: 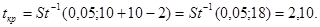
 , то можно сделать вывод, что наблюдения не согласуются с нулевой гипотезой, т. е. состав работников на предприятиях двух отраслей различен.
, то можно сделать вывод, что наблюдения не согласуются с нулевой гипотезой, т. е. состав работников на предприятиях двух отраслей различен. есть l нормальных генеральных совокупностей, из которых извлечены выборки объемом
есть l нормальных генеральных совокупностей, из которых извлечены выборки объемом 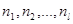 соответственно, и пусть
соответственно, и пусть 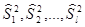 - исправленные выборочные дисперсии (2.13).
- исправленные выборочные дисперсии (2.13). .
.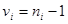 – число степеней свободы i-й выборки;
– число степеней свободы i-й выборки; для
для  , где
, где 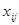 – результат j-го наблюдения i-й выборки;
– результат j-го наблюдения i-й выборки;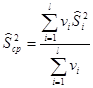 . (2.59)
. (2.59)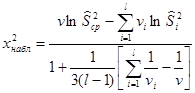 , (2.60)
, (2.60)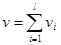 .
.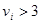 ,
,  приближенно имеет распределение
приближенно имеет распределение 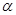 и числа степеней свободы l-1 из условия:
и числа степеней свободы l-1 из условия: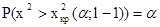 . (2.61)
. (2.61)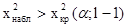 , то гипотезу отвергают, если же
, то гипотезу отвергают, если же 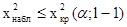 , то считают, что гипотеза не противоречит опытным данным.
, то считают, что гипотеза не противоречит опытным данным.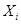 для
для 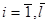 от нормального закона.
от нормального закона.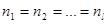 , для проверки нулевой гипотезы
, для проверки нулевой гипотезы 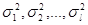 , из которых извлечены выборки объемом
, из которых извлечены выборки объемом 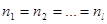 , и пусть
, и пусть 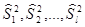 - исправленные выборочные дисперсии соответствующих совокупностей.
- исправленные выборочные дисперсии соответствующих совокупностей. . С целью проверки нулевой гипотезы Кохран предложил критерий, основанный на статистике:
. С целью проверки нулевой гипотезы Кохран предложил критерий, основанный на статистике: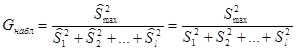 , (2.62)
, (2.62)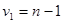 и
и 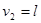 степенями свободы, где
степенями свободы, где 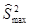 – наибольшая из исправленных выборочных дисперсий.
– наибольшая из исправленных выборочных дисперсий.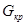 находят по таблице G-распределения (таблица 9 Приложения) из условия:
находят по таблице G-распределения (таблица 9 Приложения) из условия: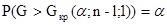 . (2.63)
. (2.63)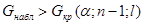 , то гипотезу отвергают, если же
, то гипотезу отвергают, если же 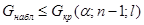 , то считают, что гипотеза не противоречит опытным данным.
, то считают, что гипотеза не противоречит опытным данным.


