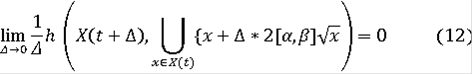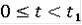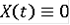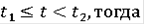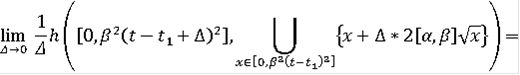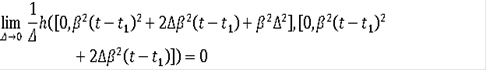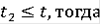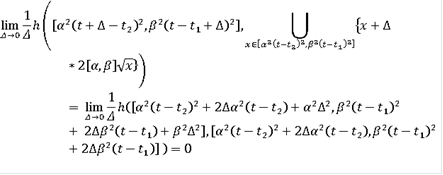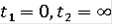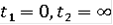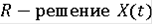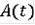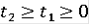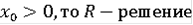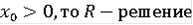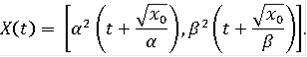Теоремы 
 Примеры.
Примеры.
Определение Непрерывная функция 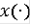
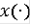 , называется решением дифференциального уравнения в паратингенциях (контингенциях), если включение (3.1.1.) (соответственно (3.1.2.)) справедливо для всех
, называется решением дифференциального уравнения в паратингенциях (контингенциях), если включение (3.1.1.) (соответственно (3.1.2.)) справедливо для всех 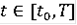
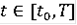 .
.
Ниже
Определение Абсолютно непрерывная функция 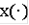
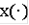 называется обычным решением дифференциального включения (3), если
называется обычным решением дифференциального включения (3), если
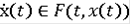
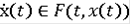 (3.2.1.)
(3.2.1.)
почти всюду на отрезке 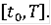
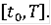
Теоремы существования обычных дифференциальных включений
Дифференциальное включение 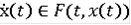
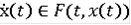 с начальным условием
с начальным условием 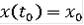
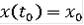 - существует, если выполняется одно из следующих условий:
- существует, если выполняется одно из следующих условий:
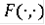
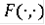 -непрерывно и
-непрерывно и 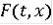
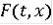 -непустое замкнутое подмножество для всех
-непустое замкнутое подмножество для всех
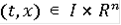
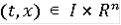
) 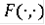
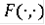 - измеримо
- измеримо
Для почти всех t, для каждой точки х, 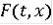
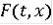 имеет замкнутый график и
имеет замкнутый график и 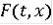
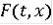 - выпукло или
- выпукло или 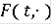
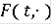 в некоторой окрестности х полунепрерывно снизу
в некоторой окрестности х полунепрерывно снизу
Функция 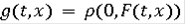
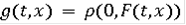 - локально интегрально ограничена, т.е. для каждого ограниченного подмножества
- локально интегрально ограничена, т.е. для каждого ограниченного подмножества 
 существует функция
существует функция 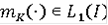
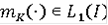 такая, что
такая, что 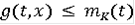
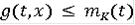 для
для 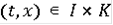
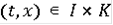
) 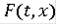
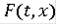 - измеримо.
- измеримо.
Для каждого t, 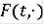
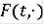 имееет замкнутый график и в каждой точке х, для которой
имееет замкнутый график и в каждой точке х, для которой 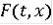
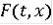 невыпукло,
невыпукло, 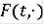
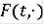 - полунепрерывно снизу.
- полунепрерывно снизу.
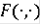
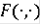 - локально слабо интегрально ограничено, т.е. для каждого
- локально слабо интегрально ограничено, т.е. для каждого 
 ,
, 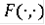
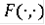 - слабо интегрально ограничено для
- слабо интегрально ограничено для 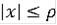
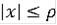 c функцией
c функцией 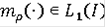
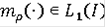 .
.
При выполнении одного из данных предположений, будет существовать хотя бы одно обычное решение включения 
 на некотором сегменте
на некотором сегменте 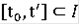
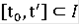 .
.
Если же в 3ем предположении заменить последнее условие на более жесткое:
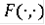
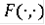 - слабо интегрально ограничено, т.е. существуют
- слабо интегрально ограничено, т.е. существуют 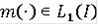
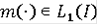 такая, что для почти всех t и x
такая, что для почти всех t и x 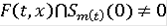
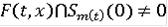 , то обычное решение дифференциального включения (3) будет существовать на всём
, то обычное решение дифференциального включения (3) будет существовать на всём 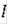
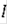 .
.
Теорема Пусть 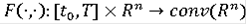
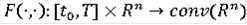 полунепрерывно сверху по
полунепрерывно сверху по 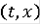
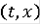 на
на 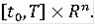
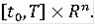 Тогда система соотношений
Тогда система соотношений
) 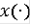
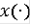 непрерывна на
непрерывна на 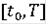
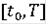 .
.
) 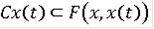
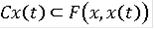 всюду на
всюду на 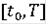
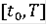 .
.
эквивалентна системе следующих соотношений:
3) 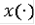
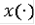 абсолютно непрерывна на
абсолютно непрерывна на 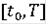
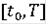 .
.
) 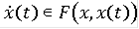
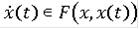 почти всюду на
почти всюду на 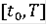
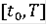 .
.
Определение Непрерывная функция 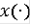
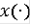 называется решением уравнения (2), если для почти всех
называется решением уравнения (2), если для почти всех 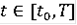
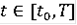
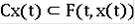
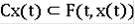 .
.
Можно сделать следующее утверждение: Пусть 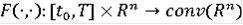
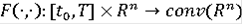 и
и
)отображение 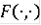
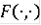 измеримо по x при каждом фиксированном х;
измеримо по x при каждом фиксированном х;
)отображение 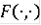
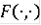 полунепрерывно по х при каждом фиксированном t.
полунепрерывно по х при каждом фиксированном t.
Тогда множество OB(F) совпадает с множеством решений в смысле последнего определения.
Но данное утверждение неверно, а указанная в нём эквивалентность не может быть получена ни при каких условиях, накладываемых на правые части, если решение уравнения в контингенциях понимается в смысле последнего уравнения. Покажем это на примере:
Пусть 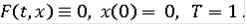
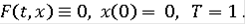 Обычным решением включения
Обычным решением включения 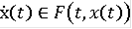
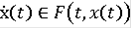 является единственная функция
является единственная функция 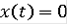
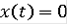 . В качестве решения уравнения в контингенциях в смысле последнего определения можно взять, например, функцию
. В качестве решения уравнения в контингенциях в смысле последнего определения можно взять, например, функцию 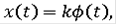
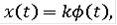 где
где 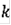
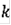 - произвольная константа, а
- произвольная константа, а 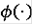
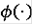 - непрерывная монотонно возрастающая функция производная которой почти всюду равна 0 и
- непрерывная монотонно возрастающая функция производная которой почти всюду равна 0 и 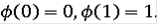
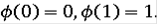 Построим такую функцию: Выберем
Построим такую функцию: Выберем 
 , зададим по индукции последовательность функций
, зададим по индукции последовательность функций 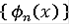
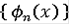 следующим образом: положим
следующим образом: положим 
 пусть
пусть 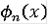
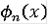 определена, непрерывна и линейна на каждом интервале вида
определена, непрерывна и линейна на каждом интервале вида 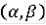
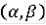 , где
, где 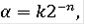
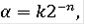
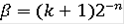
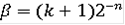 ; тогда
; тогда 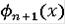
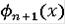 мы зададим так, чтобы
мы зададим так, чтобы 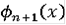
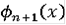 равнялось
равнялось 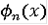
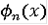 для
для 
 ; в средних точках указанных интервалов; т.е. при
; в средних точках указанных интервалов; т.е. при 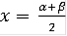
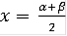 , положим
, положим
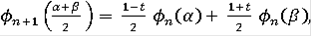
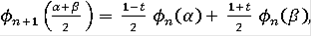
а в интервалах 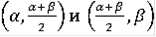
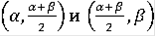 будем считать
будем считать 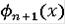
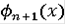 линейной. Определённые таким образом функции
линейной. Определённые таким образом функции 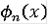
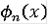 , очевидно, возрастают. Далее,
, очевидно, возрастают. Далее,
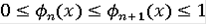
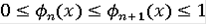
поэтому последовательность 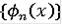
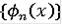 сходится к некоторой неубывающей функции
сходится к некоторой неубывающей функции 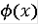
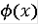 . Докажем, что
. Докажем, что 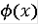
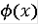 строго возрастает, непрерывна и
строго возрастает, непрерывна и
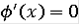
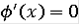
почти всюду.
Пусть x - какая-нибудь точка интервала [0,1]. Возьмем последовательность вложенных интервалов вида 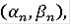
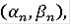 где
где
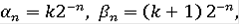
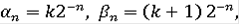
окружающих точку х. Мы имеем, очевидно,
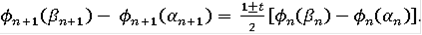
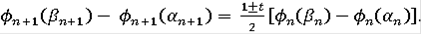
Так как 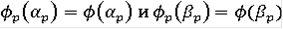
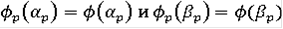 , то
, то
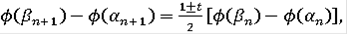
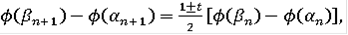
откуда получаем

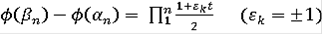 .
.
Отсюда следует, что
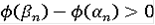
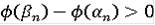
и
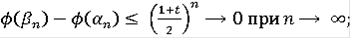
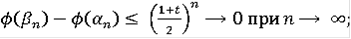
таким образом, 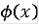
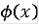 - функция непрерывная и строго возрастающая. Далее, производная
- функция непрерывная и строго возрастающая. Далее, производная 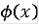
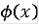 там, где она существует, равна пределу выражения
там, где она существует, равна пределу выражения
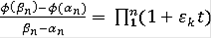
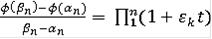
при 
 ; но такой предел либо не определён, либо бесконечен, либо, наконец, равен 0. Следовательно
; но такой предел либо не определён, либо бесконечен, либо, наконец, равен 0. Следовательно 
 во всех точках, где
во всех точках, где 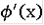
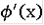 существует, т.е. почти всюду.
существует, т.е. почти всюду.
Тем самым данная функция не является абсолютно непрерывной, а значит не является решением 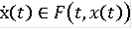
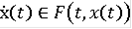 , т.е. эквивалентности решений нет. Очевидно, что данная функция будет решением любого уравнения в контингенциях в смысле последнего определения при любой правой части, которая содержит точку 0 при всех
, т.е. эквивалентности решений нет. Очевидно, что данная функция будет решением любого уравнения в контингенциях в смысле последнего определения при любой правой части, которая содержит точку 0 при всех 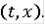
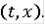
Так же очевидно, что 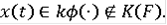
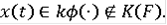
Определение Функция 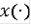
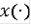 называется обобщенным решением включения (3), если
называется обобщенным решением включения (3), если 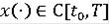
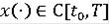 и интегральное включение
и интегральное включение
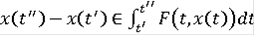
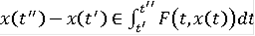 (6)
(6)
справедливо для всех 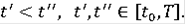
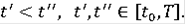
Обозначим через G(F) множество обобщенных решений включения (3).
Теорема Пусть 
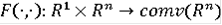 - удовлетворяет следующим условиям:
- удовлетворяет следующим условиям:
) 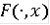
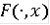 - измеримо для всех
- измеримо для всех 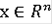
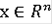 ;
;
) 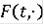
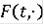 - непрерывно для всех
- непрерывно для всех 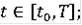
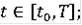
) 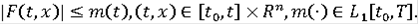
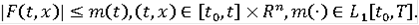
Тогда OB(F) = G(F).
Следствие Пусть 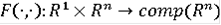
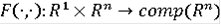 - многозначное отображение, удовлетворяющее условиям 1)-3) теоремы.
- многозначное отображение, удовлетворяющее условиям 1)-3) теоремы.
Тогда OB(conv F) = G(F).
Определение Функция 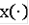
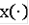 называется квазирасширением дифференциального включения (3), если существует последовательность функций
называется квазирасширением дифференциального включения (3), если существует последовательность функций 
 такая, что
такая, что
1) 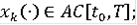
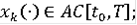
) 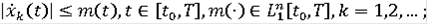
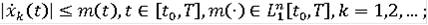
) 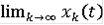
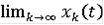 = x(t),
= x(t), 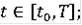
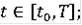
) 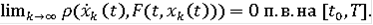
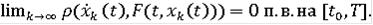
Множество квазирешений включения (3) обозначим через Q(F).
Теорема Пусть 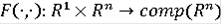
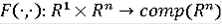 - удовлетворяет следующим условиям:
- удовлетворяет следующим условиям:
) 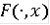
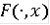 - измеримо для всех
- измеримо для всех 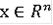
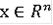 ;
;
) 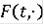
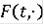 - непрерывно для всех
- непрерывно для всех 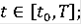
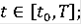
) 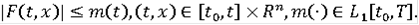
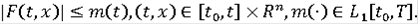
Тогда 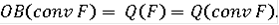
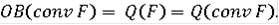
Следствие При предположениях теоремы имеем:


Определение Функция 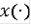
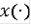 называется римановым решением дифференциального включения (3), если
называется римановым решением дифференциального включения (3), если 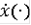
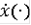 - интегрируема по Риману и
- интегрируема по Риману и 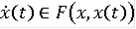
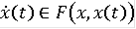 для всех
для всех 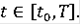
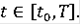
Обозначим через Ri(F) множество всех римановых решений.
Определение Функция 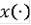
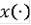 называется классическим решением дифференциального включения (3), если
называется классическим решением дифференциального включения (3), если 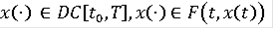
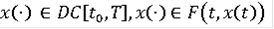 для всех
для всех 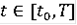
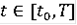 .
.
Обозначим множество всех классических решений через KL(F).
Непосредственно из определения следует, что 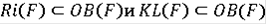
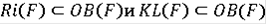 .
.
Теорема Пусть многозначное отображение F(t, x) в каждой точке (t, x) области 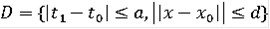
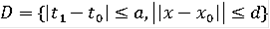 удовлетворяет следующим условиям: 1)множество F(t, x) - непусто и замкнутое;
удовлетворяет следующим условиям: 1)множество F(t, x) - непусто и замкнутое;
) F(∙,x) - измеримо на D;
)множество F(t, x) - выпукло;
) для любого r > 0 при |x - y| 
 r для почти всех t имеем
r для почти всех t имеем
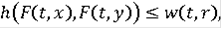
 (7)
(7)
где функция 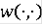
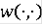 измерима по t и непрерывна по х,
измерима по t и непрерывна по х,
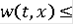
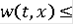
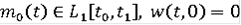
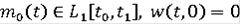 .
.
Пусть при 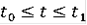
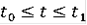 функция
функция 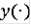
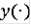 абсолютно непрерывна, её график содержится в D,
абсолютно непрерывна, её график содержится в D, 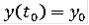
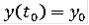 и при почти всех
и при почти всех 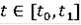
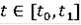
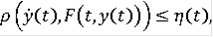
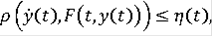
где 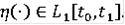
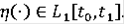
Тогда для 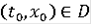
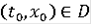 найдётся такое решение
найдётся такое решение 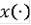
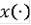 задачи
задачи
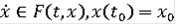
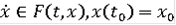 , (8)
, (8)
что
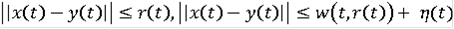
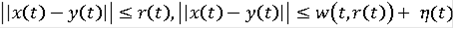 (9)
(9)
при почти всех 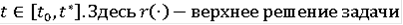
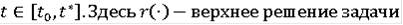
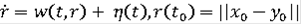
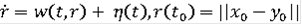 ,
,
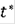
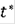 - любое такое, что
- любое такое, что 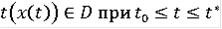
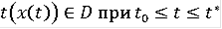 .
.
Замечание Если в данной теореме вместо условия 5) выполняется условие Липшица, т.е.
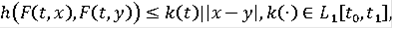
то от требования 3) можно отказаться, а в (9)
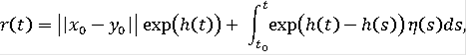
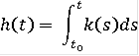
Функция 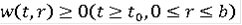
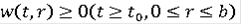 называется функцией Камке, если она непрерывна по r, измерима по t,
называется функцией Камке, если она непрерывна по r, измерима по t, 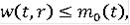
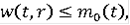
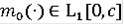
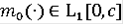 для любого c и при
для любого c и при 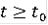
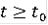 единственным решением задачи
единственным решением задачи 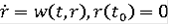
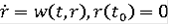 является функция
является функция 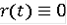
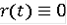 . Например, если функция
. Например, если функция 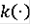
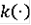 суммируема, то k(t)r - функция Камке
суммируема, то k(t)r - функция Камке 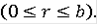
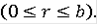
Теорема Пусть многозначное отображение 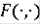
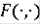 удовлетворяет следующим условиям:
удовлетворяет следующим условиям:
) множество 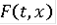
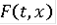 непустое и замкнутое;
непустое и замкнутое;
) 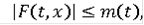
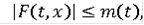 функция
функция 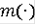
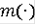 суммируема;
суммируема;
) функция 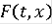
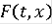 измерима по t при каждом фиксированном x;
измерима по t при каждом фиксированном x;
) 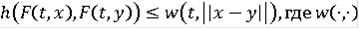
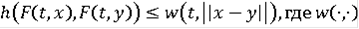 - функция Камке.
- функция Камке.
Тогда каждое решение включения
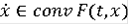
cначальным условием 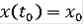
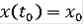 является пределом равномерно сходящейся последовательности решений включения (7).
является пределом равномерно сходящейся последовательности решений включения (7).
Теорема Пусть в ограниченной замкнутой области D выполнены следующие условия:
1) множество F(t,x) - невыпуклое и замкнуто
2) 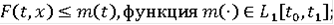
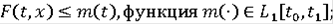
) 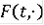
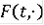 - полунепрерывна сверху на D;
- полунепрерывна сверху на D;
) 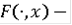
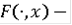 измерим на D;
измерим на D;
) множество 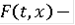
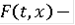 выпукло.
выпукло.
Если все решения (7) на отрезке 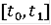
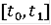 существуют и содержатся в D, то множество
существуют и содержатся в D, то множество 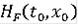
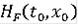 таких решений является компактом в пространстве
таких решений является компактом в пространстве 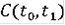
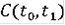 . То же самое справедливо для множества
. То же самое справедливо для множества 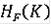
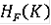 всех решений со всевозможными начальными условиями
всех решений со всевозможными начальными условиями 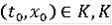
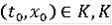 - компакт,
- компакт, 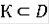
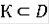 . Если К-компакт, К
. Если К-компакт, К 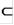
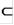 D. Если К - связный компакт (в частности, если К - точка), то множество
D. Если К - связный компакт (в частности, если К - точка), то множество 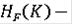
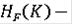 связно.
связно.
Определение Многозначная функция 
 называется R-решением, порожденным дифференциальным включением (7), если при каждом t множество R(t) замкнуто, функция R(∙) абсолютно непрерывна и для почти всех t
называется R-решением, порожденным дифференциальным включением (7), если при каждом t множество R(t) замкнуто, функция R(∙) абсолютно непрерывна и для почти всех t
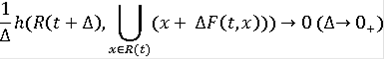
Теорема Пусть F(x, t) при каждом t, x - выпуклый компакт и как многозначная функция непрерывна по совокупности переменных. Тогда существует 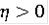
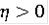 такое, что на полуинтервале
такое, что на полуинтервале 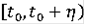
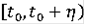 существует R- решение, попрождённое многозначной функцией F(t,x).
существует R- решение, попрождённое многозначной функцией F(t,x).
Теорема Пусть F(t,x) удовлетворяет условию Липшица в некоторой окрестности 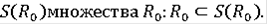
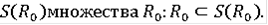 Тогда при всех
Тогда при всех 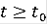
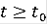 , для которых решение
, для которых решение 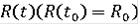
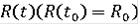 определено и
определено и 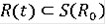
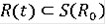 , оно единственно. Более того, имеет место непрерывная зависимость решения от начального множества
, оно единственно. Более того, имеет место непрерывная зависимость решения от начального множества 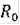
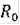 .
.
Теорема Пусть 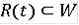
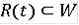 при
при 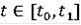
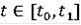 , где множество
, где множество 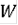
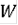 открыто и ограничено и в
открыто и ограничено и в 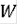
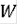 функция F(t,x) липшецева. Тогда множество R(t) при
функция F(t,x) липшецева. Тогда множество R(t) при 
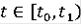 является множеством достижимости в момент t из
является множеством достижимости в момент t из 
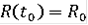 .
.
Теорема Для любого компакта 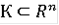
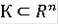 существует R-решение с начальным условием
существует R-решение с начальным условием 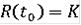
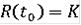 . Интегральная воронка является графиком R-решения R(∙). Если выполнено условие 5) с функцией Камке
. Интегральная воронка является графиком R-решения R(∙). Если выполнено условие 5) с функцией Камке 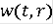
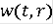 , то R- решение с начальным условием
, то R- решение с начальным условием 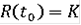
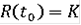 единственно, непрерывно зависит от К и его график
единственно, непрерывно зависит от К и его график 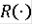
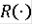 является интегральной воронкой.
является интегральной воронкой.
Пример
Пусть 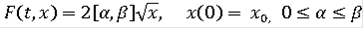
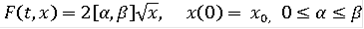 .
.
При 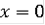
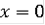 отображение
отображение 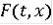
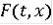 не удовлетворяет условию Липшица.
не удовлетворяет условию Липшица.
Пусть 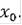
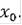 Проверим, что многозначное отображение
Проверим, что многозначное отображение
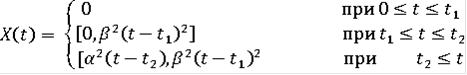
является R - решением дифференциального включения

 ,
,
т.е. удовлетворяет уравнению
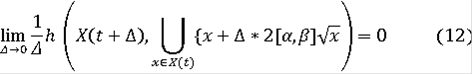
При 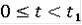
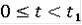 очевидно, что
очевидно, что 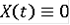
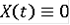 удовлетворяет (12).
удовлетворяет (12).
Пусть 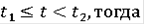
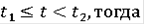
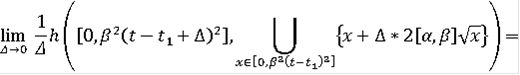
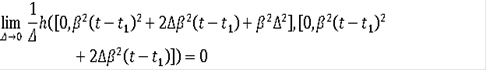
Пусть 
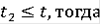
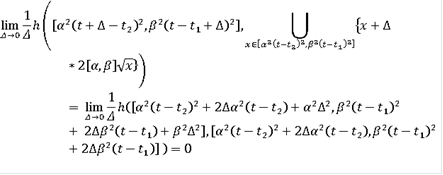
При 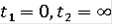
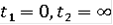
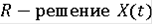
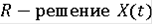 совпадает с интегральной воронкой
совпадает с интегральной воронкой 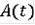
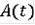 .
.
Все остальные 
 соответствующие произвольным значениям
соответствующие произвольным значениям 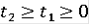
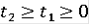 , таковы, что
, таковы, что 

Если 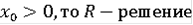
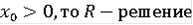
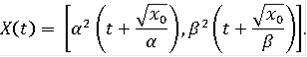
единственно и совпадает с интегральной воронкой.
Выводы
Таким образом в курсовой работе изучена теория дифференциальных включений, рассмотрен исторический аспект рассматриваемого объекта, изучены основы многозначного анализа. Для дифференциальных включений рассмотрены различные понятия решения: обычные, обобщенные и R-решения, изучены условия существования и единственности этих решений, рассмотрены примеры.




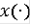
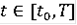
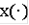
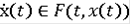
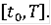
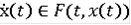
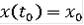
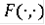
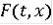
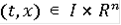
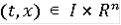
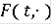
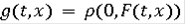
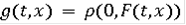 - локально интегрально ограничена, т.е. для каждого ограниченного подмножества
- локально интегрально ограничена, т.е. для каждого ограниченного подмножества 
 существует функция
существует функция 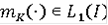
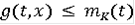
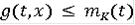 для
для 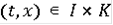
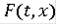
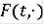
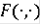

 ,
, 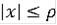
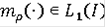

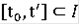
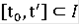 .
.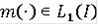
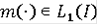 такая, что для почти всех t и x
такая, что для почти всех t и x 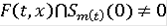
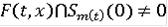 , то обычное решение дифференциального включения (3) будет существовать на всём
, то обычное решение дифференциального включения (3) будет существовать на всём 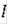
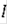 .
.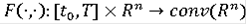
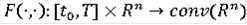 полунепрерывно сверху по
полунепрерывно сверху по 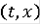
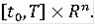
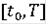
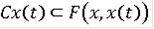
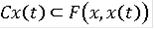 всюду на
всюду на 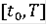 .
.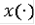
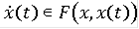
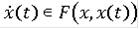 почти всюду на
почти всюду на 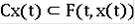
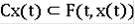 .
.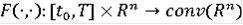
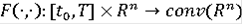 и
и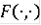
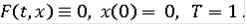
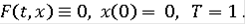 Обычным решением включения
Обычным решением включения 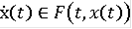
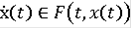 является единственная функция
является единственная функция 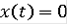
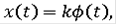
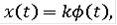 где
где 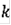
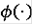
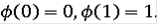
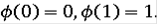 Построим такую функцию: Выберем
Построим такую функцию: Выберем 
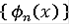
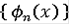 следующим образом: положим
следующим образом: положим 
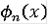
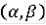
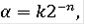
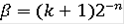
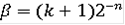 ; тогда
; тогда 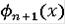
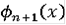
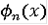

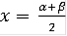
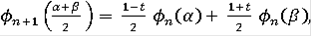
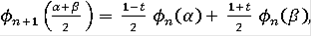
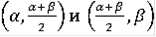
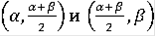 будем считать
будем считать 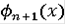 линейной. Определённые таким образом функции
линейной. Определённые таким образом функции 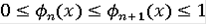
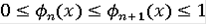
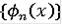
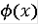
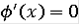
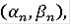
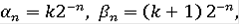
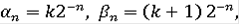
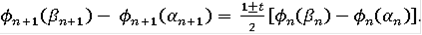
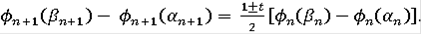
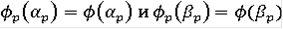
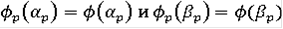 , то
, то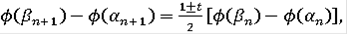
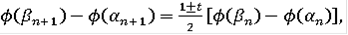

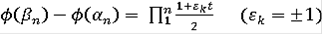 .
.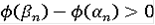
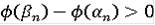
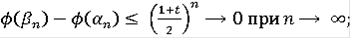
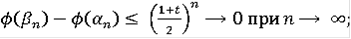
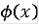
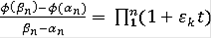
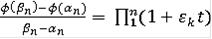


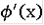
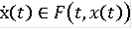
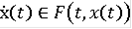 , т.е. эквивалентности решений нет. Очевидно, что данная функция будет решением любого уравнения в контингенциях в смысле последнего определения при любой правой части, которая содержит точку 0 при всех
, т.е. эквивалентности решений нет. Очевидно, что данная функция будет решением любого уравнения в контингенциях в смысле последнего определения при любой правой части, которая содержит точку 0 при всех 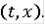
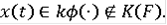
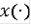
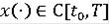
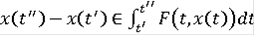
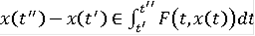 (6)
(6)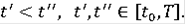

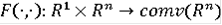 - удовлетворяет следующим условиям:
- удовлетворяет следующим условиям: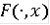
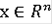
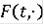
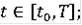
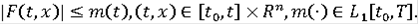
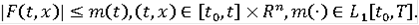
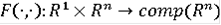
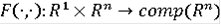 - многозначное отображение, удовлетворяющее условиям 1)-3) теоремы.
- многозначное отображение, удовлетворяющее условиям 1)-3) теоремы.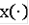

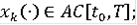
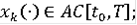
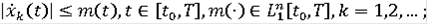
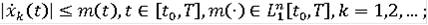
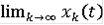
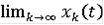 = x(t),
= x(t), 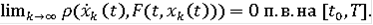
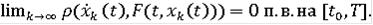
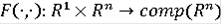
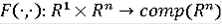 - удовлетворяет следующим условиям:
- удовлетворяет следующим условиям: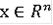
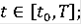
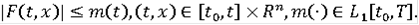
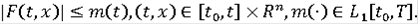
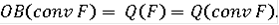
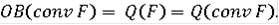


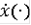
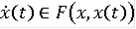
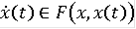 для всех
для всех 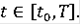
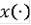
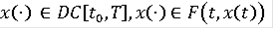
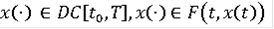 для всех
для всех 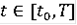
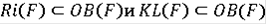
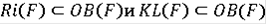 .
.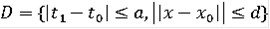
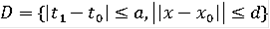 удовлетворяет следующим условиям: 1)множество F(t, x) - непусто и замкнутое;
удовлетворяет следующим условиям: 1)множество F(t, x) - непусто и замкнутое;
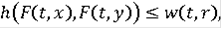
 (7)
(7)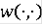
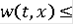
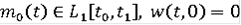
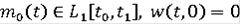 .
.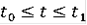
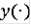
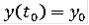
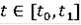
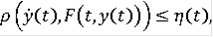
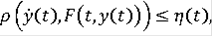
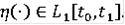
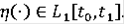
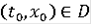
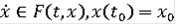
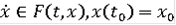 , (8)
, (8)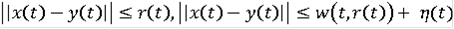
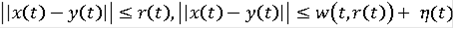 (9)
(9)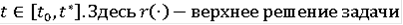
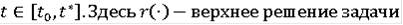
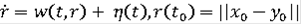
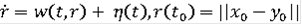 ,
,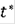
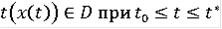
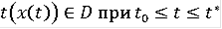 .
.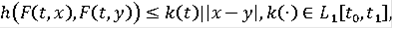
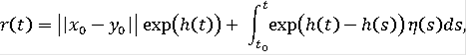
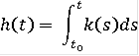
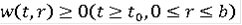
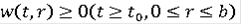 называется функцией Камке, если она непрерывна по r, измерима по t,
называется функцией Камке, если она непрерывна по r, измерима по t, 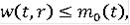
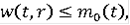
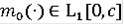
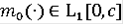 для любого c и при
для любого c и при 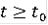
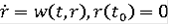
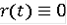
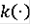
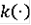 суммируема, то k(t)r - функция Камке
суммируема, то k(t)r - функция Камке 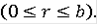
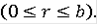
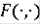
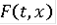
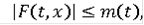
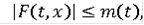 функция
функция 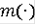
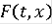
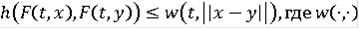
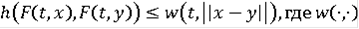 - функция Камке.
- функция Камке.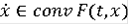
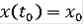
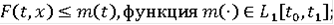
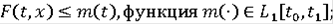
 всех решений со всевозможными начальными условиями
всех решений со всевозможными начальными условиями 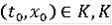
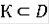
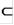
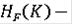

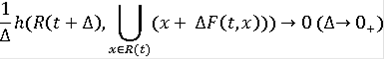
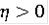
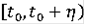
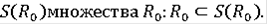
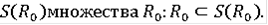 Тогда при всех
Тогда при всех 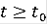
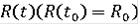
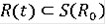
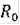
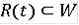
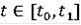
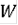
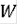

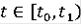 является множеством достижимости в момент t из
является множеством достижимости в момент t из 
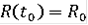 .
.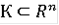
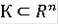 существует R-решение с начальным условием
существует R-решение с начальным условием 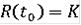
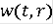
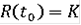
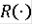
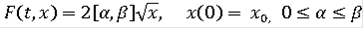
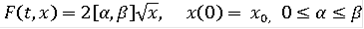 .
.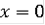
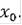
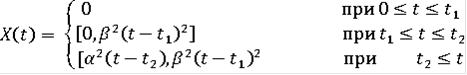

 ,
,