Определение 4. Пусть задано некоторое множество 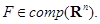 Опорной функцией множества
Опорной функцией множества 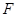 называется скалярная функция
называется скалярная функция  векторного аргумента
векторного аргумента 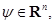 определяемая условием
определяемая условием
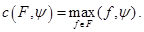
Множество 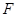 также считается одним из аргументов функции
также считается одним из аргументов функции  . Зафиксируем множество
. Зафиксируем множество 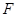 . Функция
. Функция  как функция аргумента
как функция аргумента  отображает пространство
отображает пространство 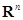 в числовую ось
в числовую ось  Максимум в правой части равенства достигается, так как скалярное произведение
Максимум в правой части равенства достигается, так как скалярное произведение 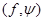 непрерывно по
непрерывно по  а множество
а множество  компактно.
компактно.
Пусть 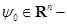 некоторый фиксированный вектор, а
некоторый фиксированный вектор, а 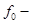 один из векторов множества
один из векторов множества 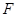 , на котором достигается максимум в определении опорной функции для вектора
, на котором достигается максимум в определении опорной функции для вектора  , то есть выполняется равенство
, то есть выполняется равенство
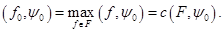
В этом случае вектор  называется опорным вектором к множеству
называется опорным вектором к множеству  в точке
в точке  , а совокупность
, а совокупность 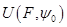 всех векторов
всех векторов 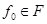 , удовлетворяющих равенству, называется опорным множеством к множеству
, удовлетворяющих равенству, называется опорным множеством к множеству 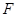 в направлении вектора
в направлении вектора 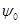 . Гиперплоскость
. Гиперплоскость 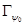 в пространстве
в пространстве 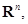 определяемая соотношением
определяемая соотношением
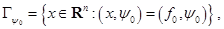
называется опорной гиперплоскостью к множеству 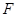 в направлении вектора
в направлении вектора 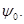
Для опорного множества 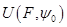 справедливо представление
справедливо представление 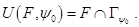
Гиперплоскость 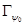 разбивает все пространство
разбивает все пространство 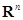 на два полупространства
на два полупространства 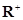 и
и 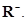 Множество
Множество 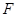 лежит в отрицательном полупространстве
лежит в отрицательном полупространстве 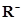 относительно вектора
относительно вектора  , так как для всех точек
, так как для всех точек  выполняется неравенство
выполняется неравенство 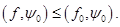
Свойства опорных функций
1. Опорная функция  положительно однородна, то есть
положительно однородна, то есть

для любого вектора 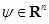 и любого числа
и любого числа  . В частности,
. В частности,  .
.
. Для любых двух векторов 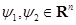 опорная функция удовлетворяет неравенству
опорная функция удовлетворяет неравенству
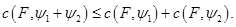
Следствие 1. Опорная функция 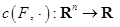 является выпуклой.
является выпуклой.
. Пусть 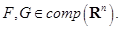 Тогда опорная функция
Тогда опорная функция 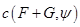 суммы
суммы 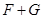 равняется сумме двух опорных функций
равняется сумме двух опорных функций  и
и 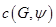 , то есть
, то есть

4. Пусть 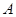 - матрица размером
- матрица размером 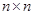 , а
, а 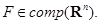 Тогда
Тогда
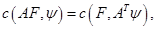
где 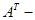 матрица, транспонированная к матрице А.
матрица, транспонированная к матрице А.
. Пусть 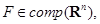 a
a 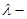 произвольное число. Тогда
произвольное число. Тогда

Следствие 2. Опорная функция  положительно однородна по первому аргументу
положительно однородна по первому аргументу  , то есть
, то есть 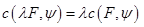 для любого числа
для любого числа 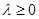 .
.
. Пусть 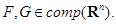 Если выполняется включение
Если выполняется включение 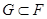 , то для любого вектора
, то для любого вектора 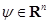 справедливо неравенство
справедливо неравенство

Следствие 3. Пусть 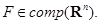 Если точка
Если точка 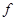 принадлежит множеству
принадлежит множеству  , то для любого вектора
, то для любого вектора 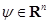 выполняется неравенство
выполняется неравенство 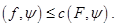
. Пусть 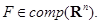 Тогда опорные функции множеств
Тогда опорные функции множеств  и
и  совпадают, то есть
совпадают, то есть
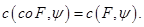
. Пусть заданы множество 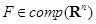 и его опорная функция
и его опорная функция  . Тогда выпуклая оболочка
. Тогда выпуклая оболочка  множества
множества  представляется в виде
представляется в виде

Здесь и далее S - единичная сфера с центром в начале координат.
9. Пусть 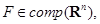
 Если для любого вектора
Если для любого вектора 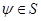 выполняется неравенство
выполняется неравенство
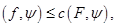
то точка 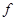 принадлежит выпуклой оболочке
принадлежит выпуклой оболочке  множества
множества 
Следствие 4. Пусть множество  В таком случае точка
В таком случае точка 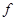 принадлежит множеству
принадлежит множеству  тогда и только тогда, когда неравенство выполняется для любого вектора
тогда и только тогда, когда неравенство выполняется для любого вектора 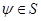 .
.
. Пусть 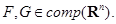 Если для любого вектора
Если для любого вектора  выполняется неравенство
выполняется неравенство

то справедливо включение GÌ coF.
Следствие 5. Пусть  и множество
и множество  выпукло. Тогда включение
выпукло. Тогда включение  справедливо тогда и только тогда, когда для любого вектора
справедливо тогда и только тогда, когда для любого вектора  выполняется неравенство (8).
выполняется неравенство (8).
. Пусть 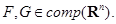 Если множества
Если множества  и
и  равны, то их опорные функции совпадают. Наоборот, если их опорные функции совпадают, то
равны, то их опорные функции совпадают. Наоборот, если их опорные функции совпадают, то 
Следствие 6. Множества 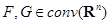 равны тогда и только тогда, когда их опорные функции совпадают. Таким образом, множество
равны тогда и только тогда, когда их опорные функции совпадают. Таким образом, множество 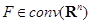 можно однозначно восстановить по его опорной функции
можно однозначно восстановить по его опорной функции 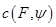 .
.
. Пусть 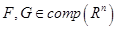 . Если множества
. Если множества  и
и  пересекаются, то есть
пересекаются, то есть 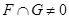 , то для любого вектора
, то для любого вектора  выполняется неравенство
выполняется неравенство
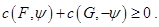
Наоборот, если выполняется соотношение для любого вектора  , то
, то 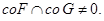
Следствие 7. Два множества  пересекаются тогда и только тогда, когда неравенство выполняется для любого вектора
пересекаются тогда и только тогда, когда неравенство выполняется для любого вектора  .
.
. Опорная функция 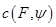 для любых двух множеств
для любых двух множеств 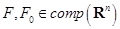 и любых двух векторов
и любых двух векторов 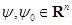 удовлетворяет неравенству
удовлетворяет неравенству
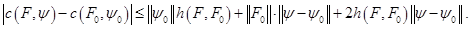
Следствие 8. Опорная функция 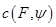 непрерывна по совокупности переменных
непрерывна по совокупности переменных 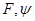 в любой точке
в любой точке  и, следовательно, непрерывна по каждой из переменных
и, следовательно, непрерывна по каждой из переменных 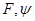 в отдельности.
в отдельности.
. Пусть 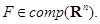 Если точка
Если точка 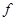 является внутренней точкой множества
является внутренней точкой множества 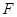 , то для любого вектора
, то для любого вектора  выполняется неравенство
выполняется неравенство
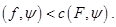
Наоборот, если соотношение выполняется для любого вектора  , то
, то 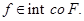
Следствие 9. Точка 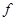 принадлежит внутренности множества
принадлежит внутренности множества 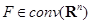
 тогда и только тогда, когда неравенство справедливо для любого вектора
тогда и только тогда, когда неравенство справедливо для любого вектора  .
.
. Пусть заданы два множества 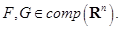 Тогда справедливо соотношение
Тогда справедливо соотношение
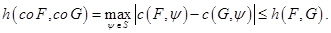
Следствие 10. Для множеств 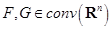 справедливо равенство
справедливо равенство
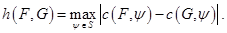
Заметим, что если множества 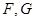 не являются выпуклыми, то в формуле может быть строгое неравенство.
не являются выпуклыми, то в формуле может быть строгое неравенство.



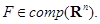 Опорной функцией множества
Опорной функцией множества 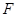 называется скалярная функция
называется скалярная функция  векторного аргумента
векторного аргумента 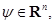 определяемая условием
определяемая условием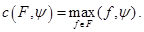
 отображает пространство
отображает пространство 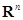 в числовую ось
в числовую ось  Максимум в правой части равенства достигается, так как скалярное произведение
Максимум в правой части равенства достигается, так как скалярное произведение 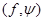 непрерывно по
непрерывно по  а множество
а множество  компактно.
компактно.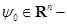 некоторый фиксированный вектор, а
некоторый фиксированный вектор, а 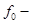 один из векторов множества
один из векторов множества  , то есть выполняется равенство
, то есть выполняется равенство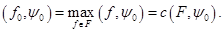
 называется опорным вектором к множеству
называется опорным вектором к множеству  , а совокупность
, а совокупность 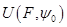 всех векторов
всех векторов 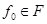 , удовлетворяющих равенству, называется опорным множеством к множеству
, удовлетворяющих равенству, называется опорным множеством к множеству 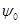 . Гиперплоскость
. Гиперплоскость 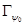 в пространстве
в пространстве 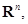 определяемая соотношением
определяемая соотношением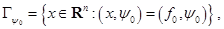
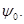
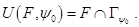
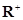 и
и 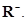 Множество
Множество 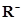 относительно вектора
относительно вектора  , так как для всех точек
, так как для всех точек  выполняется неравенство
выполняется неравенство 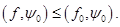
 положительно однородна, то есть
положительно однородна, то есть
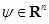 и любого числа
и любого числа  . В частности,
. В частности,  .
.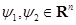 опорная функция удовлетворяет неравенству
опорная функция удовлетворяет неравенству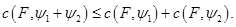
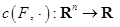 является выпуклой.
является выпуклой.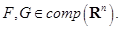 Тогда опорная функция
Тогда опорная функция 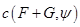 суммы
суммы 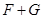 равняется сумме двух опорных функций
равняется сумме двух опорных функций  и
и 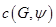 , то есть
, то есть
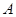 - матрица размером
- матрица размером 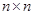 , а
, а 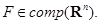 Тогда
Тогда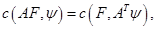
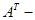 матрица, транспонированная к матрице А.
матрица, транспонированная к матрице А.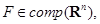 a
a 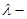 произвольное число. Тогда
произвольное число. Тогда
 , то есть
, то есть 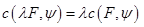 для любого числа
для любого числа 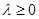 .
.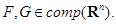 Если выполняется включение
Если выполняется включение 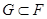 , то для любого вектора
, то для любого вектора 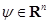 справедливо неравенство
справедливо неравенство
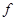 принадлежит множеству
принадлежит множеству 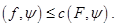
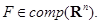 Тогда опорные функции множеств
Тогда опорные функции множеств  и
и 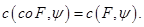
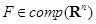 и его опорная функция
и его опорная функция  представляется в виде
представляется в виде
 Если для любого вектора
Если для любого вектора 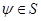 выполняется неравенство
выполняется неравенство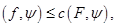

 В таком случае точка
В таком случае точка 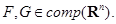 Если для любого вектора
Если для любого вектора  выполняется неравенство
выполняется неравенство
 и множество
и множество  выпукло. Тогда включение
выпукло. Тогда включение  справедливо тогда и только тогда, когда для любого вектора
справедливо тогда и только тогда, когда для любого вектора  равны, то их опорные функции совпадают. Наоборот, если их опорные функции совпадают, то
равны, то их опорные функции совпадают. Наоборот, если их опорные функции совпадают, то 
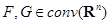 равны тогда и только тогда, когда их опорные функции совпадают. Таким образом, множество
равны тогда и только тогда, когда их опорные функции совпадают. Таким образом, множество 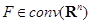 можно однозначно восстановить по его опорной функции
можно однозначно восстановить по его опорной функции 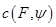 .
.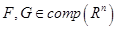 . Если множества
. Если множества 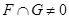 , то для любого вектора
, то для любого вектора  выполняется неравенство
выполняется неравенство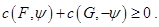
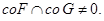
 пересекаются тогда и только тогда, когда неравенство выполняется для любого вектора
пересекаются тогда и только тогда, когда неравенство выполняется для любого вектора 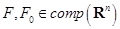 и любых двух векторов
и любых двух векторов 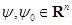 удовлетворяет неравенству
удовлетворяет неравенству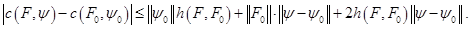
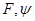 в любой точке
в любой точке  и, следовательно, непрерывна по каждой из переменных
и, следовательно, непрерывна по каждой из переменных 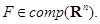 Если точка
Если точка 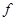 является внутренней точкой множества
является внутренней точкой множества 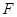 , то для любого вектора
, то для любого вектора 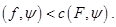
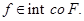
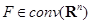
 тогда и только тогда, когда неравенство справедливо для любого вектора
тогда и только тогда, когда неравенство справедливо для любого вектора 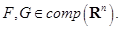 Тогда справедливо соотношение
Тогда справедливо соотношение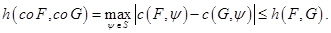
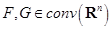 справедливо равенство
справедливо равенство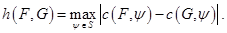
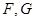 не являются выпуклыми, то в формуле может быть строгое неравенство.
не являются выпуклыми, то в формуле может быть строгое неравенство.


