Осаждение (падение) твердых тел в покоящейся жидкости или газе может быть:
- свободным, когда на падающее тело не оказывают влияние стенки емкости, где происходит осаждение, а также соседние твердые тела;
- стесненным, когда на характер осаждения тела влияют соседние тела и стенки емкости;
- стесненным осаждение однородных по крупности, плотности и форме частиц;
- стесненным осаждение неоднородных частиц.
Осаждение (движение) твердых частиц в покоящейся или сравнительно медленно движущейся жидкости или газе является, как правило, равномерным. Скорость равномерного движения твердой частицы u в достаточно большом объеме покоящейся жидкости (свободное осаждение) получило название гидравлической крупности, u0. В случае газа, когда частица находится в нем во взвешенном состоянии, говорят о скорости витания. Под этой скоростью понимают скорость вертикального потока газа, удерживающего частицу в газе во взвешенном состоянии.
Возьмем твердую частицу сферической формы диаметром d и массой m, которая осаждается в большом объеме воды. Для данного случая можно написать уравнение равновесия применительно к данной частице:
F a =G-F, (11)
где F a – сила инерции, F a =m a;
G – вес частицы с учетом ее взвешивания в воде;
F – сила полного сопротивления движению (сила лобового сопротивления).
В связи с тем, что принимается равномерное движение твердой частицы в жидкости, то при таком движении ускорение частицы а =  = 0.
= 0.
Следовательно, можно написать: G = F. Это же соотношение имеет место и при определении скорости витания частицы в газе.
Вес частицы сферической формы с учетом архимедовой силы:
G=(ρт–ρо)  , (12)
, (12)
где ρт – плотность твердой частицы;
ρо – плотность воды.
Сила лобового сопротивления при падении частицы:
F=Cφ  ρ0
ρ0  , (13)
, (13)
где uo – скорость равномерного движения частицы в воде.
Приравнивания значения G и F, и сделав некоторые преобразования, получим, что скорость осаждения (гидравлическая крупность) равна:
u0=  . (14)
. (14)
Зная значение коэффициента лобового сопротивление Cφ, зависящего от числа Рейнольдса, можно вычислить гидравлическую крупность твердой частицы.
В случае, когда ρо>ρт будет происходить всплывание частицы и скорость всплывания:
u0= 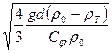 . (15)
. (15)
Однако недостатком уравнений (14) или (15) является то, что мы имеем сложные зависимости коэффициента лобового сопротивления частицы Сφ от числа Рейнольдса, а также влияние ряда других факторов.
Зависимость Сφ=f(Rе) имеет важное значение при определении гидравлической крупности (см. рис.1). При определении Сφ можно выделить четыре основных зоны (рис.1б):
1. Rе<1. В этой зоне коэффициент лобового сопротивления обратно пропорционален числу Рейнольдса, а обтекание шара является ламинарным;
2. 1<Rе<103 – коэффициент лобового сопротивления убывает не так резко, как в первой зоне, постепенно приближаясь к постоянной величине;
3. 103<Rе<105 - зона обтекания; коэффициент лобового сопротивления является приблизительно постоянным, ее называют зоной локальной автомодельности по Re;
4. 105<Rе<106– критическая зона, в которой при Rеk≈2·105÷3·105 происходит резкое падение коэффициента лобового сопротивления, т.е. кризис сопротивления.
При Re≥Rеk происходит отрыв турбулентного слоя.
При движении весьма малых частиц (Rе<1) уравнение(13) в соответствии с равенством Сφ=  приобретает вид уравнения Стокса:
приобретает вид уравнения Стокса:
u0= 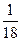 gd2
gd2  . (16)
. (16)
Некоторая степень неточности при определении u0 имеет место в связи с тем, что частицы имеют форму несколько отличную от сферической. Поэтому берется осредненная величина диаметра частицы, т.е. эквивалентный ее диаметр dэ:
dэ=  , (17)
, (17)
где W – объем твердой частицы, который соответствует объему шара диаметром dэ.
Коэффициент Сφ можно связать с числом Архимеда.
Запишем равенство G=F
(ρт-ρо)  =Cφ
=Cφ  ρ0
ρ0  . (18)
. (18)
Разделим левую и правую часть тождества (18) на константу  и сделаем некоторые преобразования (ν-кинематический коэффициент вязкости жидкости)
и сделаем некоторые преобразования (ν-кинематический коэффициент вязкости жидкости)
 . (19)
. (19)
Число Архимеда:
Аr=  . (20)
. (20)
После подстановки получим: Сφ= 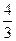
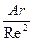 , тогда
, тогда
Число Рейнольдса
Rе=  (21)
(21)
Имея экспериментальные данные по скорости осаждения частиц в зависимости от их размеров и физических свойств жидкости, можно получить выражение Rе=f(Аr).
Результаты экспериментальных значений по Сφ, согласно данным Л. Прандтля [8], приведены в таблице 2.
Таблица 2
| Обтекание
|
| Шара
| Цилиндра
|
| Rе
| Сφ
| Аr
| Rе
| Сφ
| Аr
|
| 10–2
| 2400,00
| 0,18
| 10–2
| 628,00
| 4,7·10-2
|
| 10-1
| 245,00
| 1,84
| 10-1
| 58,00
| 43,5·10-2
|
| 1
| 28,00
| 21,00
| 1
| 10,00
| 7,5
|
| 10
| 4,40
| 3,3·102
| 10
| 2,60
| 1,9·102
|
| 102
| 1,10
| 6,2·103
| 102
| 1,45
| 1,1 104
|
| 103
| 0,46
| 3,4·105
| 103
| 0,98
| 7,4·105
|
| 104
| 0,42
| 3,2·107
| 104
| 1,12
| 8,4·107
|
| 105
| 0,49
| 3,7·109
| 105
| 1,28
| 9,2·109
|
| 106
| 0,14
| 1011
| 106
| 0,35
| 2,6·1011
|
В таблице 3 представлены значения гидравлической крупности u0 в зависимости от диаметра d частиц песчано-гравийных грунтов.
Таблица 3
| d, мм
| 0,01
| 0,03
| 0,05
| 0,08
| 0,10
| 0,13
| 0,15
| 0,18
|
| u0, мм/с
| 0,07
| 0,62
| 1,73
| 4,43
| 6,92
| 11,6
| 15,6
| 17,4
|
| d, мм
| 0,20
| 0,25
| 0,30
| 0,35
| 0,40
| 0,45
| 0,50
| 0,55
|
| u0, мм/с
| 21,6
| 27,0
| 32,4
| 37,8
| 43,2
| 48,6
| 54,0
| 59,4
|
| d, мм
| 0,60
| 0,65
| 0,70
| 0,75
| 0,80
| 0,85
| 0,9
| 0,95
|
| u0, мм/с
| 64,8
| 70,2
| 73,2
| 77,0
| 80,7
| 84,0
| 87,5
| 90,6
|
| d, мм
| 1,00
| 1,25
| 1,50
| 1,75
| 2,00
| 2,25
| 2,5
| 2,75
|
| u0, мм/с
| 94,4
| 115,0
| 125,6
| 139,2
| 152,9
| 166,2
| 176,5
| 185,0
|
| d, мм
| 3,00
| 3,25
| 3,5
| 3,75
| 4,00
| 4,25
| 4,75
| 5,00
|
| u0, мм/с
| 102,5
| 201,2
| 208,5
| 215,5
| 222,5
| 229,5
| 236,5
| 249,0
|





 = 0.
= 0. , (12)
, (12) ρ0
ρ0  , (13)
, (13) . (14)
. (14)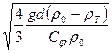 . (15)
. (15) приобретает вид уравнения Стокса:
приобретает вид уравнения Стокса: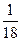 gd2
gd2  . (16)
. (16) , (17)
, (17) ρ0
ρ0  и сделаем некоторые преобразования (ν-кинематический коэффициент вязкости жидкости)
и сделаем некоторые преобразования (ν-кинематический коэффициент вязкости жидкости) . (19)
. (19) . (20)
. (20)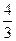
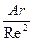 , тогда
, тогда (21)
(21)


