

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Генеалогическое древо Султанов Османской империи: Османские правители, вначале, будучи еще бейлербеями Анатолии, женились на дочерях византийских императоров...
Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов...
Интересное:
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Наиболее распространенные виды рака: Раковая опухоль — это самостоятельное новообразование, которое может возникнуть и от повышенного давления...
Дисциплины:
|
из
5.00
|
Заказать работу |
Содержание книги
Поиск на нашем сайте
|
|
|
|
ТЕЧЕНИЕ ЖИДКОСТИ С ТВЕРДЫМИ ПРИМЕСЯМИ
Общие сведения
Перемещающиеся по трубам, различным элементам жидкостных и газовых систем, каналам и руслам и т.д. жидкости и газы могут содержать твердые частицы различного размера. Частицы твердого материала, находящиеся во взвешенном состоянии в потоке жидкости или газа называются взвесями. Вместе с жидкостью или газом они образуют двухфазный поток.
Поток воздуха, в котором имеются частицы, представляет собой аэросмесь. Частички, находящиеся в потоке жидкости, образуют гидросмесь. Процесс перемещения аэросмеси называется пневмотранспортом, а гидросмеси - гидротранспортом.
Взвешенное состояние твердых частиц в жидкостях и газах поддерживается силами, возникающими в результате обтекания частиц потоком и колебаниями, вызванными турбулентными пульсациями скоростей и давления.
Характер обтекания частиц обуславливает особенности движения гидросмеси или аэросмеси по сравнению с течением однородных жидкостей и газов. Наличие взвесей влияет на взаимодействие жидкости или газа с твердыми стенками объекта, по которому осуществляется перемещение жидкостит или газа со взвесями.
Поэтому одной из основных задач при изучении такого взаимодействия является определение сил, действующих на частицу, и затрат механической энергии, обусловленных этими силами. Решение этой задачи позволяет подойти к вопросу расчета гидравлических и пневматических систем, в которых происходит перемещение и осаждение твердых частиц, находящихся в потоке жидкости или газа.
При движении гидросмеси может иметь место, как напорное так и безнапорное движение гидросмеси. Напорное движение гидросмеси осуществляется по трубам, а безнапорное в открытых руслах (лотки, желоба, каналы и безнапорные трубы). При этом основной целью исследований является определение затрат механической энергии на перемещение гидросмеси, размеров труб и русел и оптимального расхода.
Очистка жидкостей от твердых примесей. Принцип гидравлического расчета песколовок
Песколовки предназначены для выделения из сточных вод тяжелых минеральных частиц (главным образом песка). Принцип действия горизонтальной песколовки основан на том, что при движении потока сточной воды, каждая находящаяся в ней тяжелая нерастворимая частица под действием силы тяжести перемещается вниз со скоростью, равной гидравлической крупности.
Длина горизонтальной песколовки L, в пределе которой частица с гидравлической крупностью u0 при средней скорости потока V опустится на глубину Н, вычисляется по формуле:
L= 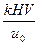 , (40)
, (40)
где k – коэффициент, учитывающий несовершенство режима работы песколовки (расслоение песка в подводящем канале и другие факторы);
V – средняя скорость движения воды в песколовке при расходе Q и площади живого сечения ω=ВН;
H – глубина протока в песколовке;
В – ширина песколовка;
u0 – гидравлическая крупность осаждаемых частиц песка.
Значение коэффициента k (по В. Калицуну) рекомендуется для горизонтальных песколовок принимать по таблице 6 в зависимости от средних размеров частиц.
Таблица 6
| Средний диаметр частиц d, мм | 0,15 | 0,2 | 0,25 | 0,3 | 0,35 | 0,4 |
| Гидравлическая крупность u0, мм/с | 13,2 | 18,7 | 24,2 | 29,7 | 35,1 | 40,7 |
| Коэффициент k | - | 1,67 | 1,38 | 1,16 | 1,11 | 1,08 |
С использованием приведенных зависимостей может производиться расчет горизонтальных отстойников различных типов, позволяющих выделять из потока взвешенные частицы [5].
Напорный гидротранспорт
Перемещение (транспортирование) различных твердых частиц потоком жидкости (воды) по трубам за счет перепада давления в трубе называется напорным гидротранспортом.
При турбулентном режиме движения потока гидросмеси в трубе твердые частицы в результате пульсации скоростей и давления участвуют в турбулентном перемешивании. Для поддержания твердых частиц во взвешенном состоянии и на преодоление сопротивления их движению затрачивается дополнительная механическая энергия по сравнению с обычным потоком жидкости.
Дополнительные потери удельной механической энергии ∆hw при движении гидросмеси обычно выражают в виде относительных удельных потерь (гидравлического уклона):
Δ i =  , (41)
, (41)
где ℓ – длина трубопровода, на котором дополнительные потери равны ∆hw.
Относительные удельные потери механической энергии при гидротранспорте можно выразить следующей функциональной зависимостью:
∆ i =(Vs, ρ0, μо , ρт, ds, z, β, D, k, α, Со), (42)
где Vs –средняя скорость гидросмеси;
ρ0, μ 0– плотность и вязкость жидкости;
ρт – плотность частички транспортируемого материала;
ds – диаметр частички;
β, z – параметры, характеризующие форму частиц и гранулометрический состав транспортируемого материала;
D – диаметр трубопровода;
k – шероховатость трубопровода;
α – угол наклона трубопровода;
Со – объемная концентрация гидросмеси.
Для определения гидравлических потерь при транспортировании гидросмеси получило распространение, следующее выражение:
i s= i о+∆ i, (43)
где i о – гидравлический уклон при движении воды в трубе:
i о=  , (44)
, (44)
λ - коэффициент гидравлического трения.
При гидротранспорте абразивных материалов, например, песка, происходит уменьшение первоначальной шероховатости труб, т.е. имеет место шлифовка внутренней ее поверхности. В связи с этим было установлено, что при расчете напорного гидротранспорта при определении коэффициента λ следует использовать формулы для гидравлически гладких труб.
Наиболее подходящей формулой, как было установлено экспериментами, для вычисления λ является формула П. Конакова для гидравлически гладких труб, при Re>105.
λ=  , (45)
, (45)
Гидравлические потери в трубопроводе при движении гидросмеси:
hℓs= i sℓ. (46)
На рис. 4 представлены кривые изменения i s от средней скорости в трубе V и плотности гидросмеси. Несущая жидкость – вода.

На этом рисунке кривая 0 - изменение гидравлического уклона в зависимости от скорости движения воды в трубе, кривые 1,2,3,4 – при движении потока гидросмеси плотностью ρs1, ρs2, ρs3, ρs4, соответственно. Плотности гидросмеси, показанные на рисунке 4, представлены в возрастающем порядке: ρs4>ρs3>ρs2>ρs1>ρо.
Минимальные гидравлические потери (гидравлический уклон) имеют место при средних скоростях, равных критической скорости Vкр. При повышении плотности гидросмеси (концентрации) увеличиваются гидравлические потери и критическая скорость. Критическая скорость Vкр является одним из основных параметров при определении гидравлических потерь в трубопроводе и оптимального режима перемещения гидросмеси.
В связи с этим наиболее достоверные зависимости по определению hws и Vкр, связаны с проведением экспериментальных исследований, в основу которых входят параметры представленные соотношением (42).
Получение теоретического решения для определения hеs в связи со сложностью физического процесса перемещения частичек в потоке представляет собой весьма большие трудности. Имеющиеся теоретические формулы разных авторов не в полной степени соответствуют данным, полученным на основании экспериментальных исследований, выполненных на гидравлических стендах и в натурных условиях [6].
Достаточно обширные экспериментальные исследования по гидротранспортированию однородных материалов были проведены Р. Дюраном в лаборатории в Гренобле [20]. В качестве транспортируемых частиц использовался в основном однородный песок крупностью d=0,2,0,44 и 2,04 мм при диаметрах трубопровода D=104;150;253;380 и 406мм. Трубы в опытах имели различную шероховатость k. Кроме песка применялись в опытах корундовый порошок, частички пластмассы и гравий крупностью до d=25мм. Объемная концентрация гидросмеси изменялась до Со=23%.Относительная плотность гидросмеси в экспериментах была в пределах 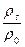 =1,5до3,95.
=1,5до3,95.
Используя теорию размерности и результаты опытов Р. Дюран предложил для определения ∆ i следующую зависимость.
∆ i =В0 i оСо[  ]n, (47)
]n, (47)
где В0 – эмпирический коэффициент, получаемый в результате проведения эксперимента; В0=81;
n – показатель степени, n=1,5.
После включения плотности частиц песка и жидкости в коэффициент В0 формула Дюрана приобретает следующий вид
∆ i =В i 0Со[  ]1,5. (48)
]1,5. (48)
Для однородного кварцевого песка плотностью ρт=2680кг/м3, В=176.
Согласно исследованиям Боннингтона для сравнительно однородного материала В=150, а по данным Бабкока и Коха В=80 [19].
В формулу 10.47 входит число Фруда
Fr= 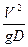 (
( ). (49)
). (49)
В зависимости (47) коэффициент лобового сопротивления Сφ характеризует размеры частиц (крупность) и форму частиц.
В исследованиях Р. Дюрана по нахождению критической скорости использовалась труба D = 150мм, по которой транспортировался песок и измельченный каменный уголь разной концентрации.
Критическая скорость по Дюрану:
Vкр=K[2gD( )]0,5, (50)
)]0,5, (50)
где К – коэффициент, определяется в зависимости от концентрации Со и диаметра частиц.
После обработки опытных данных, Дюран предложил критическую скорость находить по зависимости:
Vкр=  . (51)
. (51)
Исследования гидротранспорта разнородных песчаных и песчано-гравийных грунтов в трубах диаметром D=104÷500мм с различными концентрациями были проведены в различных институтах России. Транспортируемый материал был весьма разнообразен как по крупности, так и по форме частиц.
По предложению Л. Животовского для учета неоднородности грунта принимается осредненное значение коэффициента Сφср в зависимости от размеров фракции (грунта). Для определения ∆i Л. Животовским на основании экспериментов была предложена следующая формула:
∆i =165 i оСо[ 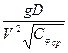 ]1,4. (52)
]1,4. (52)
Критическая скорость по Л. Животовскому:
Vкр=6,5Со0,36  . (53)
. (53)
Коэффициент лобового сопротивления Сφср при гидротранспорте существенно влияет на гидравлические потери в трубопроводе. Сφср определяется в зависимости от коэффициента а с, характеризующего гранулометрический состав грунта. Значение а с находится по следующей формуле
а с= 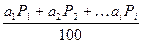 , (54)
, (54)
где а 1, а2, а i – коэффициенты, зависящие от крупности частиц грунта, определенной гранулометрическим составом (рис.3);
Р1,Р2,Рi – процентное содержание размеров фракции в грунте, соответствующий значениям а 1, а 2, а i.
В таблице 7 приведены значения коэффициентов, а в зависимости от размеров частиц грунта содержащихся во фракции
Таблица 7
| Размер фракции мм | 80÷ 40 | 40÷ 20 | 20÷ 10 | 10÷7 | 7÷5 | 5÷3 | 3÷2 | 2÷1 | 1÷ 0,5 | 0,5÷ 0,25 | 0,25÷ 0.1 | <0,1 |
| а | 1,75 | 1,8 | 2,0 | 2,0 | 1,9 | 1,7 | 1,5 | 1,2 | 0,7 | 0,4 | 0,1 | 0,02 |
Коэффициент лобового сопротивления Сφ ср находится по значению ас, определяемой по формуле (54).
Анализ отечественных натурных экспериментов по определению гидравлических потерь показал, что в формуле (52) число 165 можно рекомендовать изменить на значение86, а формулу (53) представить в виде:
Vкр=4,9Со0,33( ). (55)
). (55)
На основании обработки имеющихся экспериментальных данных, для определения i s применительно к песчаным и песчано-гравийным грунтам была предложена следующая формула:
i s= i о[(1+2(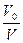 )3], (56)
)3], (56)
где V0– средняя оптимальная скорость потока гидросмеси в трубе;
V – фактическая средняя скорость гидросмеси в трубе.
Оптимальная скорость вычисляется по зависимости:
Vо=5,6· а·  , (57)
, (57)
где а – поправочный коэффициент зависящий от крупности частиц. В случае d≤10мм, а =1. При d>10мм a =1,05-1,9 [4,13];
Ψ* - коэффициент транспортабельности, параметр, определяющий фракционный состав материала (грунта).
Для разнородного материала средневзвешенное значение коэффициента транспортабельности:
Ψ*= 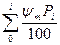 , (58)
, (58)
где Ψ* i - коэффициент транспортабельности для определенной фракции грунта (материала) d i;
Р i процентное содержание фракции d i.
Значения Ψ* i - определяются в зависимости от фракции грунта по таблице 8
Таблица 8
| Фракция грунта материала, мм | Ψ* i | Фракция грунта, мм | Ψ* i |
| 0,05-0,1 | 0,02 | 2-3 | 1,5 |
| 0,1-0,25 | 0,2 | 3-5 | 1,3 |
| 0,25-0,5 | 0,4 | 5-10 | 1,9 |
| 0,5-1 | 0,8 | 10 и более | 2 |
| 1-2 | 1,2 |
Критическую скорость в трубе предлагается вычислять по формуле:
Vкр=8,3 

 (59)
(59)
Методика определения гранулометрического состава материала не дает действительной картины распределения частиц по форме и размерам. Следовательно могут достаточно существенно различаться определяемые величины Сφ и Ψ*, это будет сказываться на расчет гидротранспорта.
Кроме этого наличие в достаточно большом количестве пылеватых и глинистых частиц в песчаном грунте приводит к уменьшению гидравлических потерь вычисляемых по предлагаемым формулам.
Расчет гидротранспорта сводится к определению критических скоростей и гидравлических потерь.
Работа гидротранспортной установки должна осуществляться при скоростях достаточно близких к критическойскорости. Правильное вычисление Vкр, как уже отличалось раньше, позволяет предотвратить осаждение сравнительно крупных частиц на дно трубы. Однако следует отметить, что при работе гидротранспортной установки расход гидросмеси и крупность материала изменяется со временем. В результате чего на дно трубопровода будет происходить осаждение твердых частичек. Слой осажденного материала – слой заиления и его называют телом заиления.
Образовавшийся слой заиления высотой ∆hs уменьшает живое сечение трубопровода. Высота слоя заиления для горизонтального трубопровода может быть вычислена по формуле:
∆hs=0,4D 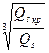 , (60)
, (60)
где Qs кр критический расход, Qsкр=Vкр  ;
;
Qs – расход гидросмеси.
Потери относительной удельной энергии в заиленных трубопроводах определяют по следующей зависимости:
i з=К i кр, (61)
где i кр – гидравлический уклон, соответствующий Vкр;
К – поправочный коэффициент при критической скорости движения гидросмеси.
К=f(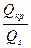 ).
).
Значение коэффициента К приведены в таблице 9.
Таблица 9
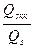
| 1 | 1,1 | 1,2 | 1,3 | 1,4 | 1,5 | 1,6 |
| К | 1 | 1,013 | 1,024 | 1,035 | 1,045 | 1,054 | 1,063 |
Для наклонных трубопроводов удельные гидравлические потери и критическая скорость вычисляются по следующим формулам:
i sн= i о+(i s– i о)cоsα; (62)
Vкрн=Vкрcоsα, (63)
где α – угол наклона трубопровода, по которому перемещается гидросмесь.
А. Юфиным для вертикальных труб удельные гидравлические потери было предложено определять по следующим формулам:
Для восходящих потоков гидросмеси:
i вос= i о(1+  ). (64)
). (64)
Для нисходящих потоков:
i н= i о(1–  ), (65)
), (65)
где i о – удельные потери напора при движении воды;
dср – средний диаметр частиц, см;
D – диаметр трубопровода, см;
u0 – гидравлическая средневзвешенная крупность частиц, см/с;
V – средняя скорость в трубе, см/с.
При расчете гидравлических потерь в местных сопротивлениях учитывается плотность гидросмеси. Опытами установлено, что гидравлические потери в местном сопротивлении увеличиваются на величину 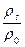 :
:
hws=ζ 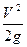
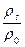 , (66)
, (66)
где ζ – коэффициент местных сопротивлений.
Безнапорный гидротранспорт
Безнапорный гидротранспорт осуществляется в открытых руслах: бетонные, земляные каналы (канавы), деревянные и железобетонные лотки, безнапорные трубы. Сечение каналов и лотков обычно прямоугольное или трапецеидальное.
Расчет безнапорных гидротранспорта сводится к определению геодезического уклона и размеров русла, расхода гидросмеси.
Основной зависимостью для расчета является формула Шези:
V=С  .
.
Коэффициент Шези определяется по формуле Маннинга:
С=  R1/6 ,
R1/6 ,
где n – шероховатость поверхности русла;
R- гидравлический радиус.
Принимается для деревянного покрытия русла n=0,013, металлического – n=0,011, земляного канала – n=0,015, бетонного или железобетонного – n=0,013.
Оптимальная (расчетная) средняя скорость в русле может быть вычислена по формуле А. Царевского:
Vоn=64 а  ·
·  , (67)
, (67)
где а – коэффициент, учитывающий неоднородность транспортируемого материала (грунта).
а = 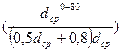 0,2 (68)
0,2 (68)
d0-80ср – осредненная величина крупности частиц материала от 0 до 80%;
dср0-80=  его грансостава;
его грансостава;
dср– средняя величина крупности всего материала;
R – гидравлический радиус русла, м;
uocp– средневзвешенная гидравлическая крупность частиц материала.
uocp= 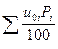 ,
,
u0 i – гидравлическая крупность частиц размером d i.
Для определения оптимальной скорости рекомендуется также следующая формула в основу, которой входит критическая скорость в русле:
Vоn=КнVкр, (69)
где Кн – коэффициент надежности, зависящий от вида транспортируемого материала (грунта), Кн=1,1÷1,3.
Для песчаных грунтов Кн=1,2, для песчано-гравийных Кн=1,3.
Критическая скорость в русле находится по следующей зависимости:
Vкр=В 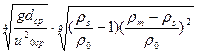 , (70)
, (70)
где В – параметр характеризующий вид транспортируемого материала. Для песчаных и песчано-гравийных грунтов В=3÷3,8.
Геодезический уклон русел определяется по формуле Шези, для воды:
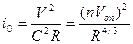 . (71)
. (71)
При гидротранспорте по руслу гидросмеси вводится поправочный коэффициент, учитывающий плотность гидросмеси и вид транспортируемого грунта.
Уклон русла канала при гидротранспорте:
i s=К i 0=  , (72)
, (72)
где Vоn - оптимальная средняя скорость в русле.
В таблице 10 приведены знания коэффициента K.
Таблица 10
| Средние скорости потока м/с | |||||||||
| Глубина,м | 1 | 2 | 3 | 1,5 | 2 | 3 | 2 | 3 | 4 |
| Плотность гидросмеси ρs,кг/м3 | Глины, суглинки К | Супеси, мелко и среднезернистый песок К | Крупнозернистый песок и песчано-гравийный грунт К | ||||||
| 1050 | 1,25 | 1,15 | 1,1 | 1,3 | 1,2 | 1,1 | 1,4 | 1,35 | 1,2 |
| 1080 | 1,4 | 1,3 | 1,25 | 1,4 | 1,4 | 1,2 | 1,6 | 1,4 | 1,35 |
| 1100 | 1,45 | 1,4 | 1,3 | 1,6 | 1,45 | 1,40 | 1,9 | 1,7 | 1,5 |
| 1120 | - | 1,45 | 1,4 | - | 1,6 | 1,45 | - | 1,9 | 1,65 |
| 1190 | - | 1,6 | 1,45 | - | 1,6 | - | - | - | |
При расчете лотков в некоторых случаях применяются таблицы для определения уклонов русел i s и оптимальных скоростей Vоn [7].
ТЕЧЕНИЕ ЖИДКОСТИ С ТВЕРДЫМИ ПРИМЕСЯМИ
Общие сведения
Перемещающиеся по трубам, различным элементам жидкостных и газовых систем, каналам и руслам и т.д. жидкости и газы могут содержать твердые частицы различного размера. Частицы твердого материала, находящиеся во взвешенном состоянии в потоке жидкости или газа называются взвесями. Вместе с жидкостью или газом они образуют двухфазный поток.
Поток воздуха, в котором имеются частицы, представляет собой аэросмесь. Частички, находящиеся в потоке жидкости, образуют гидросмесь. Процесс перемещения аэросмеси называется пневмотранспортом, а гидросмеси - гидротранспортом.
Взвешенное состояние твердых частиц в жидкостях и газах поддерживается силами, возникающими в результате обтекания частиц потоком и колебаниями, вызванными турбулентными пульсациями скоростей и давления.
Характер обтекания частиц обуславливает особенности движения гидросмеси или аэросмеси по сравнению с течением однородных жидкостей и газов. Наличие взвесей влияет на взаимодействие жидкости или газа с твердыми стенками объекта, по которому осуществляется перемещение жидкостит или газа со взвесями.
Поэтому одной из основных задач при изучении такого взаимодействия является определение сил, действующих на частицу, и затрат механической энергии, обусловленных этими силами. Решение этой задачи позволяет подойти к вопросу расчета гидравлических и пневматических систем, в которых происходит перемещение и осаждение твердых частиц, находящихся в потоке жидкости или газа.
При движении гидросмеси может иметь место, как напорное так и безнапорное движение гидросмеси. Напорное движение гидросмеси осуществляется по трубам, а безнапорное в открытых руслах (лотки, желоба, каналы и безнапорные трубы). При этом основной целью исследований является определение затрат механической энергии на перемещение гидросмеси, размеров труб и русел и оптимального расхода.
|
|
|

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Автоматическое растормаживание колес: Тормозные устройства колес предназначены для уменьшения длины пробега и улучшения маневрирования ВС при...

Таксономические единицы (категории) растений: Каждая система классификации состоит из определённых соподчиненных друг другу...

История развития хранилищ для нефти: Первые склады нефти появились в XVII веке. Они представляли собой землянные ямы-амбара глубиной 4…5 м...
© cyberpedia.su 2017-2025 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!