Пусть в (3.1.6) А - постоянная матрица,
' = A y, А = const. (3.2.1)
В этом случае построение фундаментальной системы решений, или фундаментальной матрицы сводится к алгебраическим операциям.
Будем искать частное решение системы (3.2.1) в виде aеlx, где l - неизвестный параметр, a - неизвестный постоянный столбец. Подставляя это выражение в (3.2.1), получим laelx = Aaelx. Отсюда делаем вывод, что a должно быть решением алгебраической системы уравнений
(А - lЕ) a = 0. (3.2.2)
Для того чтобы a было нетривиальным решением, нужно потребовать, чтобы
(А - lЕ) = 0. (3.2.3)
Это уравнение является алгебраическим уравнением степени n и называется характеристическим уравнением уравнения (3.2.1).
Пусть l1, …, ln - простые корпи характеристического уравнения (3.2.3). Каждому li отвечает a(i) ¹ 0 (собственный вектор матрицы А), который находится из (3.2.2), где положено l = li. В качестве компонент a(i) можно взять, например, алгебраические дополнения к одной из строк, определителя Det (А - liЕ).
Теорема 3.2.1. Пусть l1, …, ln - простые корни характеристического уравнения (3.2.3) и пусть a(i) - решение (нетривиальное) уравнения (А - liЕ) a = 0. Тогда столбцы a(i)  (i = 1,..., n) образуют фундаментальную систему решений уравнения (3.2.1).
(i = 1,..., n) образуют фундаментальную систему решений уравнения (3.2.1).
Доказательство:
Проводится но схеме, которая была использована в гл. 2 п. 2.4. Предположим, что решения a(i)  линейно зависимы:
линейно зависимы:
 . (3.2.4)
. (3.2.4)
Отсюда имеем

Дифференцируя это равенство, приходим к соотношению типа (3.2.4), содержащему уже n - 1 слагаемых. Повторяя операцию, приходим в конце концов к равенству C1 a(i) = 0. Так как хотя бы одна из компонент a(i), отлична от нуля, то получаем отсюда C1 = 0, что противоречит (3.2.4).
Обратимся к общему случаю. Пусть характеристическое уравнение (3.2.3) имеет корни l1, …, li кратностей m1,..., mi (m1 +... + mi = n). Из предыдущего ясно, что a(i)  , где a(i) - собственный вектор, отвечающий li, будет решением уравнения (3.2.1). Каждому li в рассматриваемом случае может отвечать несколько собственных векторов, но, вообще говоря, их число рi £ mi. Таким образом, решений вида a(i)
, где a(i) - собственный вектор, отвечающий li, будет решением уравнения (3.2.1). Каждому li в рассматриваемом случае может отвечать несколько собственных векторов, но, вообще говоря, их число рi £ mi. Таким образом, решений вида a(i)  может быть меньше n и они, следовательно, не образуют фундаментальной системы решений.
может быть меньше n и они, следовательно, не образуют фундаментальной системы решений.
Для того чтобы выяснить, откуда взять "недостающие" решения, потребуются некоторые построения, к которым и перейдем. Пусть у - решение уравнения (3.2.1). Тогда компоненты уi, этого решения удовлетворяют системе уравнений
i1 y1 +... + ainyn - Dyi = 0, i = l,..., n, (3.2.5)
где d - оператор дифференцирования. Определитель Det (A - ED) º M(D) представляет собой некоторый операторный многочлен n-й степени. Если вместо D подставить l, то получится левая часть характеристического уравнения (3.2.3) или характеристический многочлен системы (3.2.1). Так как умножение операторных многочленов можно производить по правилу умножения обычных многочленов, то, умножая (3.2.5) на алгебраические дополнения Аij(D) определителя Det (A - ED) (умножение понимается как умножение операторов) и суммируя по i, получаем
(D) yj = 0, j = l,..., n,
а это - дифференциальное уравнение порядка та относительно уj, характеристический многочлен которого совпадает с характеристическим многочленом системы (3.2.1). Таким образом, справедлива следующая
Теорема 3.2.2. Каждая компонента уj решения у системы (3.2.1) удовлетворяет уравнению n-го порядка, характеристический многочлен которого равен характеристическому многочлену системы (3.2.1).
Рассмотрим корень lk кратности mk. Индекс k будем в нижеследующих рассуждениях опускать, так как будем иметь дело только С одним корнем. Этому корню l отвечает решение у системы (3.2.1), j-я компонента которого yj в силу теоремы 3.2.2, имеет вид
j = (С1j + С2j х +... + Сmj xm - 1) еlx,
где Сkj = const, и, таким образом,
 (3.2.6)
(3.2.6)
В этом выражении, однако, поскольку компоненты уj, не независимы, а связаны системой (3.2.5), постоянные Сkj не являются независимыми.
Оказывается, в выражении (3.2.6) число независимых констант, Сkj равно кратности m корня l. Обоснованием этого факта мы займемся ниже, а пока выясним, что это дает для построения фундаментальной системы решении уравнения (3.2.1).
Обозначим свободные постоянные через C1,..., Cm. Подставим (3.2.6) в (3.2.1), сократим на еlx и приравняем члены с одинаковыми степенями х. Тогда получится линейная алгебраическая система m однородных уравнений с m ´ n неизвестными Ckj, которые можно выразить линейно через свободные постоянные C1,..., Cm. После этого (3.2.6) можно записать в виде
у = [С1 р1 (х) +... + Сm pm (х)] elx, (3.2.7)
где рi (х) - столбцы, компоненты которых являются вполне определенными многочленами относительно х степени не выше m - 1.
Из (3.2.7) следует, что корню характеристического уравнения l кратности m отвечают m решений вида pi (x) elx (i = l,..., m). Такое построение можно проделать для каждого lk кратности mk. В результате получим m1 +... + mi, = n решений.
Ниже будет доказано, что полученные описанным способом n решений образуют фундаментальную систему решений уравнения (3.2.1).
Практически для нахождения фундаментальной системы решений рекомендуется для каждого l написать выражение (3.2.6), затем подставить в (3.2.1) и из полученной указанным выше способом алгебраической системы выразить все постоя иные через свободные постоянные. То, что число свободных постоянных заранее известно и равно, кратности m корня l, помогает решению этой алгебраической системы, так как это означает, что заранее известен ее ранг.
Теорема 3.2.3. Существует n линейно независимых постоянных векторов (столбцов) (k = 1,..., s; jk = 1,..., qk), удовлетворяющих соотношениям
e (k1) = lk e (k1), e (k2) = lk e (k2) + e (k1) k = 1, …, s; q1 + … +qs = n, (3.2.8)
…………………………..

причем сумма qk, отвечающих одинаковым lk, равна m, где m - кратность корня lk характеристического уравнения (3.2.3).
В (3.2.8) через е (k1) обозначен собственный вектор, отвечающий lk. Векторы e (k2),...,  называются присоединенными векторами, порожденными собственным вектором e k1. Таким образом, каждому lk отвечают qk линейно независимых векторов, среди которых один собственный вектор и остальные присоединенные, а всем l1,..., ls отвечают n линейно независимых векторов. Напомним, что lk для разных k могут быть одинаковыми.
называются присоединенными векторами, порожденными собственным вектором e k1. Таким образом, каждому lk отвечают qk линейно независимых векторов, среди которых один собственный вектор и остальные присоединенные, а всем l1,..., ls отвечают n линейно независимых векторов. Напомним, что lk для разных k могут быть одинаковыми.
Рассмотрим lk. Ему заведомо отвечает решение у(k1) = e (k1) 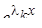 Оказывается, ему отвечает еще qk - 1 (и всего, таким образом, qk) решений, как утверждается следующей теоремой.
Оказывается, ему отвечает еще qk - 1 (и всего, таким образом, qk) решений, как утверждается следующей теоремой.
Теорема 3.2.4. Каждому lk отвечает qk решений вида
(k1) = e (k1) exp lkx,
y(k2) = (e (k2) + x e (k1)) exp (lkx),
…………………………………………… (3.2.9)
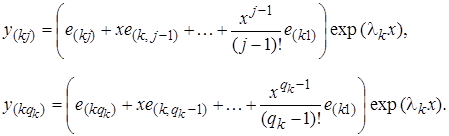
Доказательство. Это нетрудно доказать непосредственной проверкой, пользуясь (3.2.8). Действительно,


Итак, каждому lk (k = 1,..., s) отвечает qk решений вида (3.2.9), и, таким образом, всего имеется q1 +... + qs = n решений:
 (3.2.10)
(3.2.10)
Теорема 3.2.5. Решения (3.2.10) образуют фундаментальную систему решений.
Доказательство. Действительно,
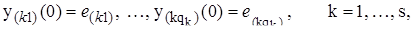
а согласно теореме 3.2.3 столбцы  в количестве q1 +... + qs = n являются линейно независимыми и, следовательно, Det W (0) ¹ 0. В силу теоремы 3.1.4 отсюда следует, что решения (3.2.10) линейно независимы, т.е. образуют фундаментальную систему решений. Вернемся теперь к прежней нумерации корней характеристического уравнения, когда нумеруются различные по величине l. Каждому l может отвечать несколько групп решений вида (3.2.10) по числу отвечающих этому l собственных векторов, по общее число решений в этих группах равно кратности m корня l. Таким образом, действительно, линейная комбинация решении, отвечающих данному l, имеет вид (3.2.6), где независимых констант будет m, так как число решений типа (3.2.10), отвечающих этому l, есть m. Заметим, что, как видно из (3.2.9), (3.2.10), старшая степень многочленов в (3.2.6), вообще говоря, меньше, чем т.е. m - 1. При практическом вычислении фундаментальной системы решений можно пользоваться (3.2.9), предварительно найдя все собственные и присоединенные векторы, но проще поступать, как указано выше, подставляя (3.2.6) в исходное уравнение (3.2.1) и выделяя m свободных неизвестных Сkj.
в количестве q1 +... + qs = n являются линейно независимыми и, следовательно, Det W (0) ¹ 0. В силу теоремы 3.1.4 отсюда следует, что решения (3.2.10) линейно независимы, т.е. образуют фундаментальную систему решений. Вернемся теперь к прежней нумерации корней характеристического уравнения, когда нумеруются различные по величине l. Каждому l может отвечать несколько групп решений вида (3.2.10) по числу отвечающих этому l собственных векторов, по общее число решений в этих группах равно кратности m корня l. Таким образом, действительно, линейная комбинация решении, отвечающих данному l, имеет вид (3.2.6), где независимых констант будет m, так как число решений типа (3.2.10), отвечающих этому l, есть m. Заметим, что, как видно из (3.2.9), (3.2.10), старшая степень многочленов в (3.2.6), вообще говоря, меньше, чем т.е. m - 1. При практическом вычислении фундаментальной системы решений можно пользоваться (3.2.9), предварительно найдя все собственные и присоединенные векторы, но проще поступать, как указано выше, подставляя (3.2.6) в исходное уравнение (3.2.1) и выделяя m свободных неизвестных Сkj.
Заключение
В ходе дипломной работы была изучена и проанализирована теория теории линейных обыкновенных дифференциальных уравнений с постоянными коэффициентами. При изучение данной теории били рассмотрены следующие разделы: линейные обыкновенные уравнения первого, второго и n-го порядков; основные свойства линейного обыкновенного уравнения второго порядка и общие свойства уравнения n-го порядка; однородные и неоднородные уравнения n-го порядка и приложение в котором показаны методы решения линейных уравнений и физических задач, решаемых с использованием линейных уравнений.
По результатом данной работы можно сделать вывод, что в настоящее время разработка методов решения этих задач для линейных обыкновенных дифференциальных уравнений продвинута на столько, что зачастую исследователь имеющий дело с этой задачей не занимается выбором метода ее решения, а просто обращается к стандартному алгоритму.
Подводя итог, следует заметить, что данная дипломная работа может быть использована для подготовки материалов методического пособия по этой теме.
Библиография
1. Бибиков Ю.Н.. Курс обыкновенных дифференциальных уравнений. - М.: Высш. Шк., 1991.-303 с.
2. Виленкин Н.Я., Доброхотова М.А., Сафонов А.Н. Дифференциальные уравнения. - М.: Просвещение, 1984. - 175 с.
3. Пискунов Н.С. Дифференциальное и интегральное исчисление.-М.:Наука,1970.-576 с.
4. Понтрягин Л.С. Обыкновенные дифференциальные уравнения. - М.: Наука,1983.
5. Самойленко А.М., Кривошея С.А., Перестюк Н.А.. Дифференциальные уравнения: примеры и задачи. - М.: Высш. Шк., 1989.-383 с.
6. Степанов В.В. Курс дифференциальных уравнений.-М.:Гостехиздат,1959.
7. Тихонов А.Н., Васильева А.Б., Свешников А.Г. Дифференциальные уравнения. - М.: Наука, 1985.-230 с.
8. Хартман Ф. Обыкновенные дифференциальные уравнения. - М.: Мир, 1970.
Приложение
I Найти общее решение уравнений:
а) yўў- 7yў + 12y = 0.
Решение:
Составим характеристическое уравнение и найдем его корни
l2-7l+12=0
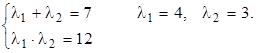
т.к. корни характеристическое уравнение различны, то общее решение данного уравнения имеет вид
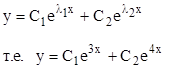
Ответ: 
б) yўў + 4yў + 13y = 0
Решение:
Характеристическое уравнение для данного уравнения имеет вид
l2 - 4l +13 = 0.

т.к. корнями характеристическое уравнение являются комплексно сопряженные числа, то общее решение заданного уравнения имеет вид
y = eax(C1 cos bx +C2 sin bx),
где a = - 2 и b = 3 Откуда= e-2x(C1 cos 3x +C2 sin 3x)
Ответ: y = e-2x(C1 cos 3x +C2 sin 3x)
в) yўў- 6yў + 9y = 0
Решение:
Составим характеристическое уравнение
l2 - 6l + 9 = 0, (l - 3)2 = 0, l1,2 = 3
т.к. корнями характеристическое уравнение имеет корень второй кратности, то общее решение для данного уравнения имеет вид
y = (C1 + C2 x) elx
Ю y = (C1 + C2 x) e3x
Ответ: y = (C1 + C2 x) e3x
Найти частные решения уравнений, удовлетворяющие указаным начальным условиям:
а) yўў - 5yў + 6y = 0, y(0) = 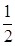 , yў(0) =1.
, yў(0) =1.
Найдем общее решение исходного уравнения, для этого составим характеристическое уравнение и найдем его корни
l2 - 5l + 6 = 0
 = C1e2x + C2e3x
= C1e2x + C2e3x
Найдем yў и значение функций y(0) и yў(0)
ў = (C1e2x + C2e3x)ў = 2C1e2x + 3C2e3x(0) = C1e2Ч0 + C2e3Ч0 =C1 + C2
yў(0) = 2C1e2Ч0 + 3C2e3Ч0 = 2C1 + 3C2
Исходя их начальных условий составим систему двух уравнений

Подставим в формулу общего решения, вместо С1 и С2 их значения и найдем частное решение
y = 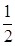 e2x + 0 Ч e3x =
e2x + 0 Ч e3x = 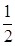 e2x
e2x
Ответ: y = 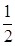 e2x
e2x
б) yўў + 4y = 0, y  = - 4, yў
= - 4, yў  = 2
= 2
l2 + 4 = 0 l2 = - 4l1,2 =± 2i= C1 cos 2x + C2 sin 2xў (C1 cos 2x + C2 sin 2x)ў = - 2C1 cos 2x + 2C2 sin 2x  = C1 cos
= C1 cos  + C2 sin
+ C2 sin 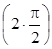 = C1 cos p+ C2 sin p = C1(-1)+C2 Ч n = - C1
= C1 cos p+ C2 sin p = C1(-1)+C2 Ч n = - C1
yў  = - C1 sin
= - C1 sin 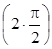 + C2 cos
+ C2 cos 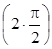 = - 2C1 Ч n +2C2(-1) = - 2C2
= - 2C1 Ч n +2C2(-1) = - 2C2

y4 cos 2x - sin 2x
Ответ: y = 4 cos 2x - sin 2x
в) yўў - 6yў + 9y = 0, y|0| = 0, yў|0| = 2
l2- 6l + 9 = 0 (l-3)2 = 0 Ю l1,2 = 3.= (C1 + C2x)e3xў =((C1 + C2x)e3x)ў = C2e3x + 3(C1 + C2x)e3x|0| = (C1 + C2 Ч 0)e3 Ч0= C1ў |0| = C2e3 Ч 0 + 3 (C1 + C2 Чn)e3 Ч 0 =C2 + 3C1
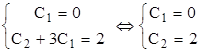 = (0 + 2x)e3x = 2xe3x
= (0 + 2x)e3x = 2xe3x
Ответ: y = 2xe3x
III. Найти общее решение следующих уравнений
yўў + 4yў +y = 4
Найдем общее решение однородного уравнения
yўў + 4yў +y = 0.
l2 + 4l +1 = 0 l1,2 = - 
Общее решение будет имеет вид
y = C1elx + C2el2X00 = C1 
Общее решение неоднократного уравнения определяется формулой
yон = yоо+yчн
Для нахождения общего решения неоднократного уравнения, осталось найти частное решение неоднократного уравнения
Частное решение имеет вид
yчн = b0
yўчн = 0, yўўчн = 0
Подставляя в исходное уравнение значения частного решения и производных получим частное решение неоднократного уравнения, т.е.
+ 4 Ч 0 + b0 = 4 Ю b0 = 4чн = 4.он = С1 
Ответ: yон = С1 
)yўў - 6yў + 9y = x2.
l2 + 6l + 9 = 0 Ю l1,2 = 3 y00 = (C1 +C2x) e3xчн =bo +b1x + b2x2
yўчн = b1 + 2b2x yўўчн = 2b22 - 6b1 - 12b2x + 9b0 + 9b1x + 9b2x2 = x2
 чн =
чн =  он = (C1 + C2)e3x +
он = (C1 + C2)e3x +  (3x2 + 4x +2)
(3x2 + 4x +2)
Ответ: yон = (C1 + C2)e3x +  (3x2 + 4x +2)
(3x2 + 4x +2)
3)yўў +6yў +9y = 12e-3x
l2 + 6l +9 = 0 l1,2 = - 3оо = (C1 + C2)e3xчн = b0x2e-3xўчн = 2 b0x2e-3x- 3b0x2e-3xўўчн = 2 b0e-3x - 6 b0xe-3x - 6 b0xe-3x + 9 b0x2e-3x = 2 b0xe-3x - 12 b0xe-3x + 9 b0x2e-3x
b0x2e-3x - 12 b0xe-3x + 2 b0xe-3x + 12 b0xe-3x - 18 b0x2e-3x + 9 b0x2e-3x =12e-3x0 = 12 Ю b0 = 6чн =6 x2e-3xон = (C1 + C2x) e-3x +6 x2e-3x
Ответ: yон = (C1 + C2x) e-3x +6 x2e-3x
4)yўў +6yў - 3y = 12 cos 3x
l2 + 6l - 3 = 0 l1,2 = - 3 ±  оо=
оо=  чн=b0 cos 3x + a0 sin 3xўон=-b0 sin 3x + a0 cos 3x, yўўчн= - b0 cos 3x - a0 sin 3x
чн=b0 cos 3x + a0 sin 3xўон=-b0 sin 3x + a0 cos 3x, yўўчн= - b0 cos 3x - a0 sin 3x
b0 cos 3x - a0 sin 3x - 6 b0 sin 3x + 6a0 cos 3x - 3b0 cos 3x - 3a0 sin 3x = 12 cos 3x

yчн=  -
- 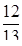 cos 3x +
cos 3x +  sin 3x
sin 3x
Ответ: yчн=  -
- 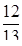 cos 3x +
cos 3x +  sin 3x
sin 3x
)yўў + 4yў = 4xe-4x
l2 + 4l = 0 l = 0, l = - 4оо = C1 + C2e- 4xчн = x(b0 + b1x)e-4xўчн = b1xe-4x + (b0 + b1x)(e-4x - 4xe-4x) = b1xe-4x + b0e-4x - 4 b0xe-4x + b1xe-4x- 4 b1x2e-4x = b0e-4x + 2 b1xe-4x - 4 b0xe-4x - 4 b1x2e-4xўўчн = - 4b0e-4x + 2b1e-4x - 8 b1 xe-4x - 4 b0e-4x + 16 b0xe-4x- 8 b1xe-4x +
+ 16b1x2e-4x = - 8 b0e-4x + 2 b0e-4 - 16 b1xe-4x +16b0xe-4x + 16 b0x2e-4x


yчн = x(-  -
- 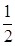 x) e- 4x = -
x) e- 4x = -  (x + 2x2) e- 4xон = C1 + C2e- 4x -
(x + 2x2) e- 4xон = C1 + C2e- 4x - 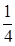 e- 4x (x + 2x2)
e- 4x (x + 2x2)
Ответ: yон = C1 + C2e- 4x -  e- 4x (x + 2x2)
e- 4x (x + 2x2)
6)yўў + y = 2x - 1 + e5x
l2 - 1 = 0 l = ± 1 Ю yоо = C1ex + C2e- xоо = C1 + C2e- 4xчн = b0 + b1x + b2e5xўчн = b1 + 5b2e5xўўчн = 0 + 25 b2e5x2e5x - b0 - b1x + b2e5x = 2x - 1+ e5x

yон = C1ex + C2e- x -2x + 1 +  e5x
e5x
Ответ: yон = C1ex + C2e- x -2x + 1 +  e5x
e5x
IV. Найти решения, удовлетворяющие заданным начальным условиям:
1)yўў + y = 3x,y(1) - 1,yў(1) = 0
l2 - 1 = 0 l = ± 1оо = C1ex + C2e- xчн = b0 + b1xўчн = b1, yўўчн = 0
- b0 + b1x =3x
 он = C1ex + C2e- x -3xчн (1) = C1e + C2e- 1 -3ўон = C1ex - C2e- x -3ўон (1) = C1e - C2e- 1 -3
он = C1ex + C2e- x -3xчн (1) = C1e + C2e- 1 -3ўон = C1ex - C2e- x -3ўон (1) = C1e - C2e- 1 -3



Ответ: 
Правило отыскания частного решения линейного неоднородного уравнения второго порядка с постоянными коэффициентами в зависимости от вида правой части уравнения
| вид правой части
| Корни характеристического уравнения
| частного решения уравнения
|
| Аm(x) - многочлен степени m
| Число 0 не является корнем характеристического уравнения
| Z = Pm(x)
|
|
| Число 0 является корнем характеристического уравнения кратности s
| Z = xs Pm(x)
|
| Am(x) Ч eaxЧисло Х не является корнем характеристического уравненияZ = Pm(x)eax
|
|
|
|
| Число Х является корнем характеристического уравнения кратности s
| Z = Pm(x) xseax
|
Am(x) cos b(x) +
| + Bm(x) sin b(x)Число ± bi не является корнем характеристического уравненияZ =Pm(x) cos bx + Qm(x) sin bx
|
|
|
Число ± bi является корнем характеристического уравнения кратности sZ = xs(Pm(x) cos bx +
eax (Am(x) cos bx +
+ Bm(x) sin bx)Число a ± i b не является корнем характеристического уравненияZ = eax (Pm(x) cos bx
Число a ± i b является корнем характеристического уравнения кратности sZ = eax (Pm(x) cos bx
V Задача. Узкая длинная трубка вращается с постоянной угловой скоростью w вокруг перпендикулярной ей вертикальной оси. В начальный момент на расстоянии an от оси внутри трубки находится шарик массы m. Считая, что в начальный момент скорость шарика относительно трубки была ровна нулю, найти закон движения шарика относительно трубки.
Решение:
Направим ось координат nx по оси трубки, приняв точку n за начало. Обозначим через x = x(1) координату шарика (точку М) в момент времени t. Так как по условию шарик движется по трубке без трения, то на него действует только центробежная сила fc = mw2x. Поэтому по второму закону Ньютона для относительного движения имеем mxўў =mwx2 или xўў - w2x = 0.
К этому уравнению присоединим начальные условия:
x (t0) = a0, xў(t0) = 0
Нормальная фундаментальная система решений уравнения имеет вид:

Использовав её, получим
x(t) = a0 ch w (t - t0)
Ответ: x(t) = a0 ch w (t - t0)
VI Задача. Один конец пружины закреплен неподвижно, а к другому прикреплен груз массы m, на который действует периодическая возмущающая сила H sin (nt + j), направленная по вертикали. При отклонении груза на расстояние x от положения равновесия пружина действует на него с силой kx (упругая сила пружины), направленной к положению равновесия; при движении груза со скоростью n сила сопротивления среды ровна bu (H > 0,n > 0, k > 0, 0 < b < m, j - постоянные). Найти движение груза в установившемся режиме и частоту вращающийся силы nрез (резонансную частоту), при которой амплитуда колебаний груза в установившимся режиме является наибольшей. Найти эту амплитуду.
Решение:
Пусть x = x(t) - отклонение груза от положения равновесия в момент времени t. Согласно второму закону Ньютона, 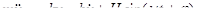 , от суда для определения для определения закона движения x = x(t) груза получаем линейное неоднородное уравнение вида:
, от суда для определения для определения закона движения x = x(t) груза получаем линейное неоднородное уравнение вида:

Поскольку p > 0, q > 0, а установившиеся движение груза существует и описывается решением данного уравнения вида:

Частоту nрез, при которой амплитуда А(n) колебаний груза в установленном режиме достигает наибольшего значения, можно найти из условия минимума функций
y(n) = (q -n2)2 + p2n2. Имеем
yў(n) = - 4n (q - n2)2 +2p2n =, откуда
nрез = 
амплитуда колебаний груза при резонансе такова:

Ответ: 
Пример: Найти фундаментальную систему решений
¢1 = 4y1 - y2,y¢2 = 3y1 + y2 - y3,y¢3 = y1 + y3. (1)
Решение:
Характеристическое уравнение, отвечающее этой системе, имеет корень l1 = 2 кратности m1 = n = 3.
 (2)
(2)
Подставляя его в (1), сокращая на е 2x и приравнивая члены с одинаковыми степенями x, получим следующие 9 уравнений для определения 9 коэффициентов:
 (3)
(3)
Заранее известно, что ранг этой системы равен 6 и свободных неизвестных 3.
Записывая определитель этой системы, расположив неизвестные в порядке a0, b0, с0, a1, b1, с1, a2, b2, с2, легко видеть, Что правый верхний определитель 6-го порядка отличен от нуля и равен, очевидно, произведению диагональных элементов, т.е. 8, так как справа от главной диагонали - нули. Следовательно, в качестве свободных неизвестных можно взять a0, b0, с0.
Первая группа уравнении (3) уже дает выражения для a1, b1, с1, через a0, b0, с0, а подставляя это во вторую группу уравнений" (3), получим
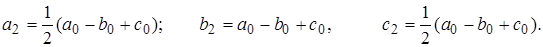
Третья группа уравнений (3) обращается автоматически в тождество.
Подставляя полученные выражения в (2) и приводя его к виду (3.2.7), будем, иметь
 (4)
(4)
Здесь a0, b0, с0 - произвольные постоянные (можно ид обозначить C1, С2, С3, как в (3.2.7), векторы р1(х), р2(х), р3(х) усматриваются в правой части (4). Таким образом, получено решение системы (3.2.1) в виде линейной комбинации трех линейно независимых решений pi (x) e 2x (i = 1, 2, 3).



 (i = 1,..., n) образуют фундаментальную систему решений уравнения (3.2.1).
(i = 1,..., n) образуют фундаментальную систему решений уравнения (3.2.1). . (3.2.4)
. (3.2.4)
 , где a(i) - собственный вектор, отвечающий li, будет решением уравнения (3.2.1). Каждому li в рассматриваемом случае может отвечать несколько собственных векторов, но, вообще говоря, их число рi £ mi. Таким образом, решений вида a(i)
, где a(i) - собственный вектор, отвечающий li, будет решением уравнения (3.2.1). Каждому li в рассматриваемом случае может отвечать несколько собственных векторов, но, вообще говоря, их число рi £ mi. Таким образом, решений вида a(i)  может быть меньше n и они, следовательно, не образуют фундаментальной системы решений.
может быть меньше n и они, следовательно, не образуют фундаментальной системы решений. (3.2.6)
(3.2.6)
 называются присоединенными векторами, порожденными собственным вектором e k1. Таким образом, каждому lk отвечают qk линейно независимых векторов, среди которых один собственный вектор и остальные присоединенные, а всем l1,..., ls отвечают n линейно независимых векторов. Напомним, что lk для разных k могут быть одинаковыми.
называются присоединенными векторами, порожденными собственным вектором e k1. Таким образом, каждому lk отвечают qk линейно независимых векторов, среди которых один собственный вектор и остальные присоединенные, а всем l1,..., ls отвечают n линейно независимых векторов. Напомним, что lk для разных k могут быть одинаковыми.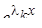 Оказывается, ему отвечает еще qk - 1 (и всего, таким образом, qk) решений, как утверждается следующей теоремой.
Оказывается, ему отвечает еще qk - 1 (и всего, таким образом, qk) решений, как утверждается следующей теоремой.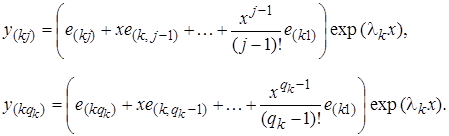


 (3.2.10)
(3.2.10)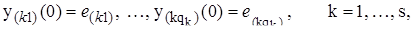
 в количестве q1 +... + qs = n являются линейно независимыми и, следовательно, Det W (0) ¹ 0. В силу теоремы 3.1.4 отсюда следует, что решения (3.2.10) линейно независимы, т.е. образуют фундаментальную систему решений. Вернемся теперь к прежней нумерации корней характеристического уравнения, когда нумеруются различные по величине l. Каждому l может отвечать несколько групп решений вида (3.2.10) по числу отвечающих этому l собственных векторов, по общее число решений в этих группах равно кратности m корня l. Таким образом, действительно, линейная комбинация решении, отвечающих данному l, имеет вид (3.2.6), где независимых констант будет m, так как число решений типа (3.2.10), отвечающих этому l, есть m. Заметим, что, как видно из (3.2.9), (3.2.10), старшая степень многочленов в (3.2.6), вообще говоря, меньше, чем т.е. m - 1. При практическом вычислении фундаментальной системы решений можно пользоваться (3.2.9), предварительно найдя все собственные и присоединенные векторы, но проще поступать, как указано выше, подставляя (3.2.6) в исходное уравнение (3.2.1) и выделяя m свободных неизвестных Сkj.
в количестве q1 +... + qs = n являются линейно независимыми и, следовательно, Det W (0) ¹ 0. В силу теоремы 3.1.4 отсюда следует, что решения (3.2.10) линейно независимы, т.е. образуют фундаментальную систему решений. Вернемся теперь к прежней нумерации корней характеристического уравнения, когда нумеруются различные по величине l. Каждому l может отвечать несколько групп решений вида (3.2.10) по числу отвечающих этому l собственных векторов, по общее число решений в этих группах равно кратности m корня l. Таким образом, действительно, линейная комбинация решении, отвечающих данному l, имеет вид (3.2.6), где независимых констант будет m, так как число решений типа (3.2.10), отвечающих этому l, есть m. Заметим, что, как видно из (3.2.9), (3.2.10), старшая степень многочленов в (3.2.6), вообще говоря, меньше, чем т.е. m - 1. При практическом вычислении фундаментальной системы решений можно пользоваться (3.2.9), предварительно найдя все собственные и присоединенные векторы, но проще поступать, как указано выше, подставляя (3.2.6) в исходное уравнение (3.2.1) и выделяя m свободных неизвестных Сkj.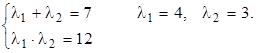
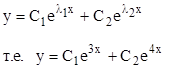


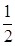 , yў(0) =1.
, yў(0) =1. = C1e2x + C2e3x
= C1e2x + C2e3x
 = - 4, yў
= - 4, yў  = C1 cos
= C1 cos  + C2 sin
+ C2 sin 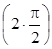 = C1 cos p+ C2 sin p = C1(-1)+C2 Ч n = - C1
= C1 cos p+ C2 sin p = C1(-1)+C2 Ч n = - C1
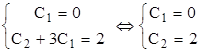 = (0 + 2x)e3x = 2xe3x
= (0 + 2x)e3x = 2xe3x


 чн =
чн =  он = (C1 + C2)e3x +
он = (C1 + C2)e3x +  (3x2 + 4x +2)
(3x2 + 4x +2) оо=
оо=  чн=b0 cos 3x + a0 sin 3xўон=-b0 sin 3x + a0 cos 3x, yўўчн= - b0 cos 3x - a0 sin 3x
чн=b0 cos 3x + a0 sin 3xўон=-b0 sin 3x + a0 cos 3x, yўўчн= - b0 cos 3x - a0 sin 3x
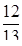 cos 3x +
cos 3x +  sin 3x
sin 3x

 -
- 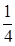 e- 4x (x + 2x2)
e- 4x (x + 2x2)
 e5x
e5x он = C1ex + C2e- x -3xчн (1) = C1e + C2e- 1 -3ўон = C1ex - C2e- x -3ўон (1) = C1e - C2e- 1 -3
он = C1ex + C2e- x -3xчн (1) = C1e + C2e- 1 -3ўон = C1ex - C2e- x -3ўон (1) = C1e - C2e- 1 -3




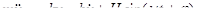 , от суда для определения для определения закона движения x = x(t) груза получаем линейное неоднородное уравнение вида:
, от суда для определения для определения закона движения x = x(t) груза получаем линейное неоднородное уравнение вида:



 (2)
(2) (3)
(3)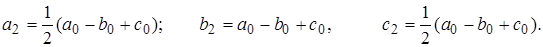
 (4)
(4)


