Обратимся к изучению уравнения
 , (2.2.1)
, (2.2.1)
коэффициенты которого  непрерывны на интервале X. Как было показано в предыдущем параграфе, решение начальной задачи существует и единственно на X, чем будем существенно пользоваться ниже.
непрерывны на интервале X. Как было показано в предыдущем параграфе, решение начальной задачи существует и единственно на X, чем будем существенно пользоваться ниже.
Определение. Будем говорить, что функции u1(x), …, up(x) линейно зависимы на интервале X, если существуют постоянные С1, …, Сp не все равные нулю, такие, что имеет место тождество
 (2.2.2)
(2.2.2)
В противном случае (т.е. если (2.2.2) выполняется только при С1 = … = Сp = 0) будем говорить, что u1(x), …, up(x) линейно независимы.
Определение. Назовём детерминант
D(x)=  (2.2.3)
(2.2.3)
определителем Вронского
Теорема 2.1. Если решения у1(x), …, уn(x) уравнения (2.2.1) линейно зависимы на X, то  .
.
В самом деле, согласно (2.2.2) имеем
 .
.
Продифференцировав это тождество (n-1) раз, получим
 (2.2.5)
(2.2.5)
При любом  эти соотношения можно рассматривать как систему линейных однородных алгебраических уравнений относительно С1, …, Сn, имеющую нетривиальное решение по условию линейной зависимости функций уi. Следовательно, определитель системы
эти соотношения можно рассматривать как систему линейных однородных алгебраических уравнений относительно С1, …, Сn, имеющую нетривиальное решение по условию линейной зависимости функций уi. Следовательно, определитель системы  при любом
при любом  , т.е.
, т.е.  на Х.
на Х.
Замечание. Из доказательства теоремы видно, что она справедлива не только для решений уравнения (2.2.1), но для любых (n-1) раз дифференцируемых функций.
Теорема 2.2. Если  хотя бы для одного
хотя бы для одного  , то решения у1(x),…, уn(x) уравнения (2.2.1) линейно зависимы на X.
, то решения у1(x),…, уn(x) уравнения (2.2.1) линейно зависимы на X.
Доказательство.
Возьмём точку x = x0 в которой  , и составим систему линейных алгебраических уравнений относительно С1,…, Сn с определением
, и составим систему линейных алгебраических уравнений относительно С1,…, Сn с определением  :
:
 (2.2.6)
(2.2.6)
Так как  , то эта система имеет нетривиальное решение С1, …, Сn. Рассмотрим линейную комбинацию
, то эта система имеет нетривиальное решение С1, …, Сn. Рассмотрим линейную комбинацию
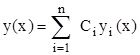 .
.
Согласно теореме 1.4 у(x) является решением уравнения (2.2.1), а (2.2.6) означает, что это решение удовлетворяет в точке x0 нулевым начальным условиям у(х0) = 0,…, у(n-1)(x0) = 0. Так как тривиальное решение уравнения (2.2.1)  удовлетворяет, очевидно, тем же начальным условиям, то, в силу теоремы единственности, у(x)
удовлетворяет, очевидно, тем же начальным условиям, то, в силу теоремы единственности, у(x) 
 (x)
(x)  0, т.е.
0, т.е. 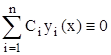 , где по настроению не все С1 равны нулю, а это и означает линейную зависимость у1(x), …, уn(x).Что и требовалось.
, где по настроению не все С1 равны нулю, а это и означает линейную зависимость у1(x), …, уn(x).Что и требовалось.
Из доказанных теорем непосредственно вытекает следующая альтернатива.
Теорема 2.3. Определитель Вронского D(x) либо тождественно равен нулю, и это означает, что решения у1(x), …, yn(x) линейно зависимы, либо не обращается в нуль ни в одной точке Х, и это означает, что у1(x), …, yn(x) линейно независимы.
Ситуацию можно выразить следующей схемой:
D(x)= 
при любом x  Х.
Х.
Определение. Фундаментальной системой решений уравнения (2.2.1) будем называть любые n линейно независимых решений уравнения (2.2.1)
Теорема 2.4. Линейное однородное уравнение имеет фундаментальную систему решений.
Доказательство.
Действительно, возьмём произвольный отличный от нуля определитель D0 с элементами  . Определим решения у1(x), …, уn(x) уравнения (1.2.1) следующими начальными условиями:
. Определим решения у1(x), …, уn(x) уравнения (1.2.1) следующими начальными условиями:
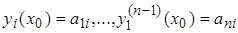 (4.7)
(4.7)
Составим определитель Вронского D(x). В силу (2.2.7) D(x0) = D0  0. А тогда, в силу теоремы 1.3, у1(x), …, уn(x) линейно независимы.
0. А тогда, в силу теоремы 1.3, у1(x), …, уn(x) линейно независимы.
Замечание. Так как существует бесконечно много определителей, отличных от нуля, для каждого уравнения существует бесконечно много фундаментальных систем решений. Кроме того, линейное невырожденное преобразование

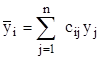
переводит одну фундаментальную систему решений в другую.
Докажем теперь основную теорему данного параграфа.
Теорема 2.5. Если у1(x), …, уn(x) - фундаментальная система решений, то любое решение у(x) уравнения (2.2.1) представимо в виде
 , (2.2.8)
, (2.2.8)
где С1, …, Сn - некоторые постоянные.
Доказательство.
Пусть у(х0) = у10, …, уn-1(х0) = уn0. Определим постоянные С1, …, Сn линейной системой уравнений с детерминантом, равным D(х0)  0:
0:
 (2.2.9)
(2.2.9)
и построим  . Согласно теореме 1.4.
. Согласно теореме 1.4.  (x) является решением уравнения (2.2.1), а (2.2.9) означает, что это решение удовлетворяет тем же начальным условиям, что и у(x). Тогда, в силу единственности,
(x) является решением уравнения (2.2.1), а (2.2.9) означает, что это решение удовлетворяет тем же начальным условиям, что и у(x). Тогда, в силу единственности,
 .Что и требовалось.
.Что и требовалось.
Замечание. Формула (2.2.8), где С1, …, Сn - произвольные постоянные, является общим решением уравнения (2.2.1), т.е. (2.2.8) является формулой, содержащей все решения уравнения (2.2.1) и не содержащей ничего, кроме решений. В самом деле, по теореме 1.4 при любых С1, …, Сn (2.2.8) является решением уравнения (2.2.1), а согласно только что доказанной теореме в (2.2.8) содержится любое решение уравнения (2.2.1).
Замечание. На языке линейной алгебры теоремы 2.4 и 2.5 означают, что в пространстве решений линейного однородного уравнения (2.2.1) имеется базис из n элементов, т.е. это пространство n-мерное.



 , (2.2.1)
, (2.2.1) непрерывны на интервале X. Как было показано в предыдущем параграфе, решение начальной задачи существует и единственно на X, чем будем существенно пользоваться ниже.
непрерывны на интервале X. Как было показано в предыдущем параграфе, решение начальной задачи существует и единственно на X, чем будем существенно пользоваться ниже. (2.2.2)
(2.2.2) (2.2.3)
(2.2.3) .
. .
. (2.2.5)
(2.2.5) эти соотношения можно рассматривать как систему линейных однородных алгебраических уравнений относительно С1, …, Сn, имеющую нетривиальное решение по условию линейной зависимости функций уi. Следовательно, определитель системы
эти соотношения можно рассматривать как систему линейных однородных алгебраических уравнений относительно С1, …, Сn, имеющую нетривиальное решение по условию линейной зависимости функций уi. Следовательно, определитель системы  при любом
при любом  , т.е.
, т.е.  на Х.
на Х. , то решения у1(x),…, уn(x) уравнения (2.2.1) линейно зависимы на X.
, то решения у1(x),…, уn(x) уравнения (2.2.1) линейно зависимы на X. , и составим систему линейных алгебраических уравнений относительно С1,…, Сn с определением
, и составим систему линейных алгебраических уравнений относительно С1,…, Сn с определением  :
: (2.2.6)
(2.2.6) , то эта система имеет нетривиальное решение С1, …, Сn. Рассмотрим линейную комбинацию
, то эта система имеет нетривиальное решение С1, …, Сn. Рассмотрим линейную комбинацию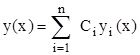 .
. удовлетворяет, очевидно, тем же начальным условиям, то, в силу теоремы единственности, у(x)
удовлетворяет, очевидно, тем же начальным условиям, то, в силу теоремы единственности, у(x) 
 (x)
(x) 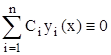 , где по настроению не все С1 равны нулю, а это и означает линейную зависимость у1(x), …, уn(x).Что и требовалось.
, где по настроению не все С1 равны нулю, а это и означает линейную зависимость у1(x), …, уn(x).Что и требовалось.
 Х.
Х. . Определим решения у1(x), …, уn(x) уравнения (1.2.1) следующими начальными условиями:
. Определим решения у1(x), …, уn(x) уравнения (1.2.1) следующими начальными условиями: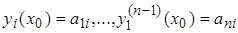 (4.7)
(4.7) 0. А тогда, в силу теоремы 1.3, у1(x), …, уn(x) линейно независимы.
0. А тогда, в силу теоремы 1.3, у1(x), …, уn(x) линейно независимы.
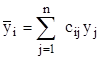
 , (2.2.8)
, (2.2.8) 0:
0: (2.2.9)
(2.2.9) . Согласно теореме 1.4.
. Согласно теореме 1.4.  (x) является решением уравнения (2.2.1), а (2.2.9) означает, что это решение удовлетворяет тем же начальным условиям, что и у(x). Тогда, в силу единственности,
(x) является решением уравнения (2.2.1), а (2.2.9) означает, что это решение удовлетворяет тем же начальным условиям, что и у(x). Тогда, в силу единственности, .Что и требовалось.
.Что и требовалось.


