Линейным дифференциальным уравнением n-го порядка называется уравнение вида
 (1.2.1)
(1.2.1)
Это уравнение обладает рядом замечательных свойств, облегчающих его исследование, а в ряде случаев и решение.
Ознакомимся с основными свойствами линейного уравнения на примере уравнения маятника

 ,
,  , (1.2.2)
, (1.2.2)
которое является линейным уравнением второго порядка с постоянными коэффициентами.
Рассмотрим сначала случай  . В этом случае уравнение называется однородным. Физически это означает, что маятник движется свободно, на него не действуют внешние (вынуждающие) силы,
. В этом случае уравнение называется однородным. Физически это означает, что маятник движется свободно, на него не действуют внешние (вынуждающие) силы,
 (1.2.3)
(1.2.3)
Будем искать решение этого уравнения в виде  , где
, где  - некоторая неизвестная заранее постоянная. Подставляя искомый вид решения в (1.2.3) и сокращая на
- некоторая неизвестная заранее постоянная. Подставляя искомый вид решения в (1.2.3) и сокращая на  , получим
, получим
 (1.2.4)
(1.2.4)
Это уравнение называется характеристическим уравнением дифференциального уравнения (1.2.3).
Ему должно удовлетворять  для того, чтобы
для того, чтобы  было решением (1.2.3). Решая уравнение (1.2.4), получим
было решением (1.2.3). Решая уравнение (1.2.4), получим

Исследуем разные случаи.
а)  . Физически это соответствует достаточно сильному трению (сопротивлению) среды. Оба корня l1 и l2 в этом случае действительны, различны и отрицательны, и им отвечают два решения
. Физически это соответствует достаточно сильному трению (сопротивлению) среды. Оба корня l1 и l2 в этом случае действительны, различны и отрицательны, и им отвечают два решения

Рассмотрим начальную задачу.
 (1.2.5)
(1.2.5)
Для любых двух n раз дифференцируемых функций y1(x), у2(x) справедливо тождество (С1 и С2 - константы)
(С1у1(x)+С2у2(x))(n) =С1у1(n)+С2у2(n) (1.2.6)
Основываясь на этом тождестве, нетрудно убедиться, что выражение
 (1.2.7)
(1.2.7)
где С1 и С2 - произвольные постоянные (линейная комбинация у(1) и у(2) является решением уравнения (1.2.3). Эти постоянные можно однозначно определить из начальных условий (1.2.5). Действительно, подставляя (1.2.7) в (1.2.5), имеем
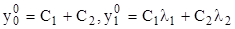
В силу l1  l2 определитель этой линейной алгебраической системы относительно С1 и С2 отличен от нуля. Полученное таким образом решение начальной задачи
l2 определитель этой линейной алгебраической системы относительно С1 и С2 отличен от нуля. Полученное таким образом решение начальной задачи
 , (1.2.8)
, (1.2.8)
не осцилируя, приближается с ростом t к положению равновесия у = 0.
Так как любое наперёд заданное решение уравнения (1.2.3) удовлетворяет некоторому начальному условию (1.2.5), а по заданному начальному условию (1.2.5) однозначно определяется решение (1.2.8), то можно сказать, что в формуле (1.2.7) содержится любое решение (1.2.3). С другой стороны, при любых значениях постоянных формула (1.2.7) даёт некоторое решение уравнения (1.2.3). Таким образом, формула (1.2.7) содержит все решения уравнения (1.2.3) и только решения этого уравнения. Формулу, обладающую таким свойством, мы будем называть общим решением. Формула (1.2.7) представляет собой общее решение уравнения (1.2.3).
б) a2 - 4k < 0. Физически это соответствует достаточно слабому трению (сопротивлению) среды. В этом случае l2 и l1 являются комплексно сопряжёнными: l2 = l  и
и

где 
 .
. 
Пользуясь тождеством (1.2.6), нетрудно видеть, что у1 = Rе у(1), у2 = Im у(1) также являются решениями уравнения (1.2.2). Действительно,

откуда, приравнивая нулю отдельно вещественную и мнимую части, получим требуемое. Возьмём линейную комбинацию у1 и у2:
 (1.2.9)
(1.2.9)
Нетрудно убедиться, что, как и прежде, С1 и С2 однозначно определяются условиями (1.2.5) и, таким образом, (1.2.9) является общим решением уравнения (1.2.3). Заметим, что в рассматриваемом случае в качестве общего решения можно по-прежнему взять (1.2.7), но при этом постоянные С1 и С2 будут комплексными.
Решение задачи (1.2.5):
 (1.2.10)
(1.2.10)
описывает колебательный процесс. Колебания затухают по закону 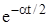 . С ростом t это решение также стремится к положению равновесия у = 0.
. С ростом t это решение также стремится к положению равновесия у = 0.
Если a = 0 (сопротивление отсутствует), то получаем периодические колебания с частотой w0= 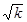 ,
,
 (2.11)
(2.11)
в) a2-4 k = 0. В этом случае описанный способ даёт только одно решение у(1) = elt, где l= -  . Нетрудно, однако, непосредственно проверить, что в этом случае решением является также у(2) = telt. Беря линейную комбинацию этих двух решений, можно удовлетворить условиям (1.2.5). Практически l1 и l2 не бывают в точности равны, но такое решение описывает математическую абстракцию, соответствующую случаю близких l1 и l2.
. Нетрудно, однако, непосредственно проверить, что в этом случае решением является также у(2) = telt. Беря линейную комбинацию этих двух решений, можно удовлетворить условиям (1.2.5). Практически l1 и l2 не бывают в точности равны, но такое решение описывает математическую абстракцию, соответствующую случаю близких l1 и l2.
Рассмотрим теперь вынужденные колебания под действием периодической вынуждающей силы. Они описываются уравнением (1.2.2), где f = А соs wt (А, w = соnst). Сопоставим этому уравнению следующее уравнение с комплексной неизвестной функцией z:
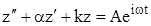 (1.2.12)
(1.2.12)
Подставляя в это уравнение  и приравнивая отдельно действительные и мнимые части, получим, что
и приравнивая отдельно действительные и мнимые части, получим, что  1, удовлетворяет уравнению (1.2.2), в котором f = А соs wt, а
1, удовлетворяет уравнению (1.2.2), в котором f = А соs wt, а  - уравнению (1.2.2), в котором f = А sin wt. Таким образом, для получения требуемого решения уравнения (1.2.2) нужно найти решение уравнения (1.2.12) и взять его действительную часть.
- уравнению (1.2.2), в котором f = А sin wt. Таким образом, для получения требуемого решения уравнения (1.2.2) нужно найти решение уравнения (1.2.12) и взять его действительную часть.
Решение уравнения (1.2.12) естественно искать в виде
 , (1.2.13)
, (1.2.13)
где  - неизвестная заранее постоянная. Подставляя (1.2.13) в (1.2.12) и сокращая на еiwt, найдём
- неизвестная заранее постоянная. Подставляя (1.2.13) в (1.2.12) и сокращая на еiwt, найдём
 и, следовательно,
и, следовательно,
 (1.2.14)
(1.2.14)
(1.2.14) представляет собой частное решение уравнения (1.2.2), в котором f = А соs wt, имеющее периодический характер с частотой, равной частоте w вынуждающей силы. Это решение, однако, не удовлетворяет (1.2.5). Добавим к нему линейную комбинацию решения однородного уравнения (1.2.3) (для определённого a2 - 4k < 0):
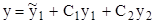 (1.2.15)
(1.2.15)
Пользуясь (1.2.6), убеждаемся, что это выражение является решением того же неоднородного уравнения (1.2.2), пользуясь произволом выбора С1 и С2 можно подобрать их так, чтобы удовлетворить (1.2.5). Действительно, С1 и С2 находятся из алгебраической системы уравнений, отличающейся от той, которая была при получении (1.2.10), только неоднократными членами. Решение, удовлетворяющее (1.2.5), имеет вид

а, (1.2.15), таким образом является общим решением неоднородного уравнения (1.2.2), где f = Асоswt. Из (1.2.15) видно, что общее решение неоднородного уравнения представляет собой сумму частного решения того же неоднородного уравнения и общего решения соответствующего однородного уравнения.
С ростом t в формуле (1.2.16) все члены, кроме первого затухают и остаются только вынужденные колебания  1.
1.
Обратим внимание на важное явление - так называемое явление резонанса. Решение  1 теряет смысл, если в исходной системе нет трения (a= 0) и частота w вынуждающей силы равна частоте w0=
1 теряет смысл, если в исходной системе нет трения (a= 0) и частота w вынуждающей силы равна частоте w0=  , с которой колеблется маятник без воздействия вынуждающей силы в (1.2.14), так как в знаменателе появляется нуль.
, с которой колеблется маятник без воздействия вынуждающей силы в (1.2.14), так как в знаменателе появляется нуль.
Чтобы найти частное решение в этом случае, т.е. частное решение уравнения
у"+kу = Асоsw0t, (1.2.17)
перейдём снова к комплексной форме
z"+ kz = Аеiw0t (1.2.18)
Обратим внимание на то, корни характеристического уравнения равны l1,2 = ± iw0. Попытаемся искать z в виде
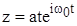 (1.2.19)
(1.2.19)
Подставляя (1.2.19) в (1.2.18), определим a и получим

 даёт частное решение уравнения (1.2.17):
даёт частное решение уравнения (1.2.17):
 (1.2.20)
(1.2.20)
Так как практически полное отсутствия трения и точное равенство w и w0 не осуществляются, то решение такого типа практически не реализуется. Реализуется (1.2.14), но если частота w близка к w0, а w мало, то знаменатель в (1.2.14) мал и амплитуда решения велика. Таким образом, физически явление резонанса состоит в том, что при w ~ w0 и малом a наблюдается заметное увеличение амплитуды вынужденных колебаний (1.2.14).
Математически же случаем резонанса будем называть такой случай, когда в (1.2.2)  , где S(t) - многочлен, а À совпадает с корнем характеристического уравнения. В рассмотренном выше уравнении (1.2.18) À = iw0, т.е. совпадает с одним из корней характеристического уравнения.
, где S(t) - многочлен, а À совпадает с корнем характеристического уравнения. В рассмотренном выше уравнении (1.2.18) À = iw0, т.е. совпадает с одним из корней характеристического уравнения.
Итак, на примере уравнения второго порядка выявлен ряд характерных свойств линейного уравнения с постоянными коэффициентами. Оказывается, эти закономерности имеют общий характер. Сформулируем их для уравнения порядка и как естественное обобщение того, что наблюдалось для уравнения второго порядка.
Рассмотрим сначала однородное уравнение

 (1.2.21)
(1.2.21)
Сопоставим (1.2.21)его характеристическое уравнение (сравним с (1.2..4)).
 ln+
ln+ 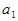 ln-1+...+
ln-1+...+  = 0 (1.2.22)
= 0 (1.2.22)
Это алгебраическое уравнения порядка и имеет корни

Если все lk действительны и различны, то беря линейную комбинацию
 где
где  (1.2.23)
(1.2.23)
можно получит любое решение уравнения (1.2.21), определяя С1,…,Cn из начальных условий
у(t0) = y10, у΄(t0) = у20,…, у(n-1)(t0) = уn0 (1.2.24)
(сравнивая с (1.2.7) и (1.2.5)), т.е. формула (1.2.23) является общим решением уравнения (1.2.21).
Если некоторые lk комплексные, то утверждение 1 остаётся в силе, но определяемые из (1.2.24) константы Ck будут комплексными и решение будет представлено в комплексной форме. Чтобы получить решение в действительной форме, в наборе решений вместо пары решений  и
и  , отвечающих двум комплексно сопряжённым корням l =p
, отвечающих двум комплексно сопряжённым корням l =p  iq (так как характеристическое уравнение имеет действительные коэффициенты, то вместе с l = p + iq корнем будет также у
iq (так как характеристическое уравнение имеет действительные коэффициенты, то вместе с l = p + iq корнем будет также у  =p-iq), можно взять пару действительных решений Re y = ept соsqt и Im y = еpt sinqt (сравнивая с (1.2.9)).
=p-iq), можно взять пару действительных решений Re y = ept соsqt и Im y = еpt sinqt (сравнивая с (1.2.9)).
Если l - кратный корень характеристического уравнения (1.2.22) кратности m, то ему отвечает m решений еlt, telt,…, tm-1e lt (обобщение случая в), где m = 2).
Объединяя все случаи, можно сформулировать следующее правило:
Пусть характеристическое уравнение (1.2.22) имеет r действительных корней lк кратности mк, а прочие являются комплексно сопряжёнными вида ll=pl+iql и кратности ml.
Тогда общее решение уравнения (1.2.21) может быть записано в виде
 (1.2.25)
(1.2.25)
где R  (t), Р
(t), Р  l(t),Q
l(t),Q  (t)-многочлены степени m
(t)-многочлены степени m  -1, m
-1, m  -1, m
-1, m  -1 соответственно, коэффициенты которых произвольны. Эти коэффициенты однозначно определяются начальными условиями (2.24).
-1 соответственно, коэффициенты которых произвольны. Эти коэффициенты однозначно определяются начальными условиями (2.24).
Точно так же можно, обобщая факты, полученные для уравнения второго порядка, сформулировать правило построения частного и общего решений неоднородного уравнения
 0у(n) +
0у(n) +  1у(n-1) + … +
1у(n-1) + … +  nу = S(t)eÀt (1.2.26)
nу = S(t)eÀt (1.2.26)
где S(t) - многочлен степени s,À- постоянная, вообще говоря, комплексная.
Пусть в уравнении (1.2.26) À не совпадает ни с одним корнем lk характеристического уравнения (1.2.22) (так называемый нерезонансный случай).
Тогда частное решение уравнения (1.2.26) можно записать в виде
у = Т(t)еÀt, (1.2.27)
где Т(t) - многочлен той же степени, что и S(t).
Коэффициенты многочлена Т(t) определяются из алгебраических уравнений, полученных подставкой (1.2.27) в (2.26) и приравниванием членов с одинаковыми степенями t (сравнивая с (1.2.12), (1.2.13); в этом простейшем случае S(t) является константой А, т.е. многочленом нулевой степени, а многочлен Т(t) также является константой: Т = 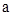 ).
).
Если À совпадает с корнем характеристического уравнения l, имеющим кратность m (так называемый резонансный случай), то частное решение (1.2.26) следует искать в виде
у = Т(t) tmeÀt, (1.2.28)
где Т(t) - многочлен той же степени, что и S(t). Коэффициенты Т(t) по-прежнему определяются подстановкой (1.2.28) в уравнение (1.2.26) (сравнивая с (1.2.19), где появляется множитель t в соответствии с кратностью m=1 корня w0)
Если À= a + ib комплексно, то действительная (соответственно мнимая) часть решения (2.28) является решением уравнения с правой частью S(t)eat соsat (соответственно S(t)eatsin at).
Общее решение неоднократного уравнения (1.2.26) представляется в виде суммы общего решения (1.2.25) однородного уравнения (1.2.21) и частного решения (1.2.27) или (1.2.28) неоднородного уравнения (1.2.26) (сравнивая с (1.2.15)).



 (1.2.1)
(1.2.1)
 ,
,  , (1.2.2)
, (1.2.2) . В этом случае уравнение называется однородным. Физически это означает, что маятник движется свободно, на него не действуют внешние (вынуждающие) силы,
. В этом случае уравнение называется однородным. Физически это означает, что маятник движется свободно, на него не действуют внешние (вынуждающие) силы, (1.2.3)
(1.2.3) , где
, где  - некоторая неизвестная заранее постоянная. Подставляя искомый вид решения в (1.2.3) и сокращая на
- некоторая неизвестная заранее постоянная. Подставляя искомый вид решения в (1.2.3) и сокращая на  , получим
, получим (1.2.4)
(1.2.4) для того, чтобы
для того, чтобы  было решением (1.2.3). Решая уравнение (1.2.4), получим
было решением (1.2.3). Решая уравнение (1.2.4), получим
 . Физически это соответствует достаточно сильному трению (сопротивлению) среды. Оба корня l1 и l2 в этом случае действительны, различны и отрицательны, и им отвечают два решения
. Физически это соответствует достаточно сильному трению (сопротивлению) среды. Оба корня l1 и l2 в этом случае действительны, различны и отрицательны, и им отвечают два решения
 (1.2.5)
(1.2.5) (1.2.7)
(1.2.7)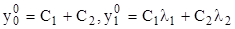
 l2 определитель этой линейной алгебраической системы относительно С1 и С2 отличен от нуля. Полученное таким образом решение начальной задачи
l2 определитель этой линейной алгебраической системы относительно С1 и С2 отличен от нуля. Полученное таким образом решение начальной задачи , (1.2.8)
, (1.2.8) и
и

 .
. 
 (1.2.9)
(1.2.9) (1.2.10)
(1.2.10)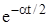 . С ростом t это решение также стремится к положению равновесия у = 0.
. С ростом t это решение также стремится к положению равновесия у = 0.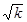 ,
, (2.11)
(2.11) . Нетрудно, однако, непосредственно проверить, что в этом случае решением является также у(2) = telt. Беря линейную комбинацию этих двух решений, можно удовлетворить условиям (1.2.5). Практически l1 и l2 не бывают в точности равны, но такое решение описывает математическую абстракцию, соответствующую случаю близких l1 и l2.
. Нетрудно, однако, непосредственно проверить, что в этом случае решением является также у(2) = telt. Беря линейную комбинацию этих двух решений, можно удовлетворить условиям (1.2.5). Практически l1 и l2 не бывают в точности равны, но такое решение описывает математическую абстракцию, соответствующую случаю близких l1 и l2.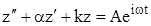 (1.2.12)
(1.2.12) и приравнивая отдельно действительные и мнимые части, получим, что
и приравнивая отдельно действительные и мнимые части, получим, что  1, удовлетворяет уравнению (1.2.2), в котором f = А соs wt, а
1, удовлетворяет уравнению (1.2.2), в котором f = А соs wt, а  - уравнению (1.2.2), в котором f = А sin wt. Таким образом, для получения требуемого решения уравнения (1.2.2) нужно найти решение уравнения (1.2.12) и взять его действительную часть.
- уравнению (1.2.2), в котором f = А sin wt. Таким образом, для получения требуемого решения уравнения (1.2.2) нужно найти решение уравнения (1.2.12) и взять его действительную часть. , (1.2.13)
, (1.2.13) - неизвестная заранее постоянная. Подставляя (1.2.13) в (1.2.12) и сокращая на еiwt, найдём
- неизвестная заранее постоянная. Подставляя (1.2.13) в (1.2.12) и сокращая на еiwt, найдём и, следовательно,
и, следовательно, (1.2.14)
(1.2.14)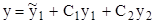 (1.2.15)
(1.2.15)
 1.
1. , с которой колеблется маятник без воздействия вынуждающей силы в (1.2.14), так как в знаменателе появляется нуль.
, с которой колеблется маятник без воздействия вынуждающей силы в (1.2.14), так как в знаменателе появляется нуль.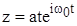 (1.2.19)
(1.2.19)
 даёт частное решение уравнения (1.2.17):
даёт частное решение уравнения (1.2.17): (1.2.20)
(1.2.20) , где S(t) - многочлен, а À совпадает с корнем характеристического уравнения. В рассмотренном выше уравнении (1.2.18) À = iw0, т.е. совпадает с одним из корней характеристического уравнения.
, где S(t) - многочлен, а À совпадает с корнем характеристического уравнения. В рассмотренном выше уравнении (1.2.18) À = iw0, т.е. совпадает с одним из корней характеристического уравнения.
 (1.2.21)
(1.2.21) ln+
ln+ 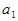 ln-1+...+
ln-1+...+  = 0 (1.2.22)
= 0 (1.2.22)
 где
где  (1.2.23)
(1.2.23) и
и  , отвечающих двум комплексно сопряжённым корням l =p
, отвечающих двум комплексно сопряжённым корням l =p  iq (так как характеристическое уравнение имеет действительные коэффициенты, то вместе с l = p + iq корнем будет также у
iq (так как характеристическое уравнение имеет действительные коэффициенты, то вместе с l = p + iq корнем будет также у  =p-iq), можно взять пару действительных решений Re y = ept соsqt и Im y = еpt sinqt (сравнивая с (1.2.9)).
=p-iq), можно взять пару действительных решений Re y = ept соsqt и Im y = еpt sinqt (сравнивая с (1.2.9)). (1.2.25)
(1.2.25) (t), Р
(t), Р  l(t),Q
l(t),Q  0у(n) +
0у(n) + 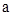 ).
).


