Пример 3. Решить уравнения
| a) log3 x + log3(x + 3) = log3(x + 24),
|
| b) log4(x 2 - 4 x + 1) - log4(x 2 - 6 x + 5) = -1/2
|
| c) log2 x + log3 x = 1
|
| |
| |
Решение. a) ОДЗ уравнения есть множество x (0;+) которое определяется из системы неравенств (условия существования логарифмов уравнения)
| 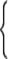
| x > 0,
|
| x +3 > 0,
|
| x +24 > 0.
|
Используя свойство P2 и утверждение 1, получим
| log3 x + log3(x + 3) = log3(x + 24)
| | | 
| log3 x (x + 3) = log3(x + 24),
| | x > 0,
| |
|

| x (x + 3) = x + 24,
| | x > 0,
| | | 
| x 2 + 2 x - 24 = 0,
| | x > 0,
| | 
| 
| x 1 = -6,
| | x 2 = 4,
| | | x > 0,
| | x = 4.
|
| | | | | | |
b) Используя свойство P3, получим следствие исходного уравнения

откуда, используя определение логарифма, получим

или
x 2 - 4 x + 1 = 1/2(x 2 - 6 x + 5),
откуда получаем уравнение
x 2 - 2 x - 3 = 0
с решениями x 1 = -1 и x = 3. После проверки остается лишь x = -1.
c) ОДЗ уравнения: x (0;+). Используя свойство P5, получим уравнение


log2 x (1 + log32) = 1,
откуда 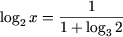 или
или  или log2 x = log63. Следовательно,
или log2 x = log63. Следовательно, 
Логарифмические неравенства
Неравенство, содержащее неизвестное под знаком логарифма или в его основании называется логарифмическим неравенством. В процессе решения логарифмических неравенств часто используются следующие утверждения относительно равносильности неравенств и учитываются свойства монотонности логарифмической функции.
Утверждение 1. Если a > 1, то неравенство log a f (x) > log a g (x) равносильно системе неравенств
| 
| f (x) > g (x),
|
| g (x) > 0.
|
Утверждение 2. Если 0 < a < 1, то неравенство log a f (x) > log a g (x) равносильно системе неравенств
| 
| f (x) < g (x),
|
| f (x) > 0.
|
Утверждение 3. Неравенство log h (x) f (x) > log h (x) g (x) равносильно совокупности систем неравенств
| 
| 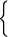
| h (x) > 1,
|
| f (x) > g (x) > 0,
|
| 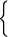
| 0 < h (x) < 1,
|
| 0 < f (x) < g (x).
|
Подчеркнем, что в неравенстве log a f (x) > log a g (x) вместо знака > может фигурировать любой из знаков ≥, <, ≤. В этом случае утверждения 1-3 соответственно преобразуются.
Пример 1. Решить неравенства
| a) log3(x 2 - x) ≥ log3(x + 8);
| |
b) 
| |
c) 
| |
Решение. a) Используя утверждение 1, получим
| log3(x 2 - x) ≥ log3(x + 8) 
| x 2 - x ≥ x + 8,
| 
| x 2 - 2 x - 8 ≥ 0,
| |
| x +8 > 0,
| x > -8,
|
b) Основание логарифма число между нулем и единицей, поэтому, используя утверждение 2, получим
c) Запишем 0 = log21 и, используя утверждение 1, получим
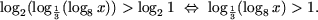
Запишем 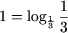 и, используя утверждение 2, получим
и, используя утверждение 2, получим

Показательные уравнения и неравенства
Показательные уравнения
Показательным называется уравнение, в котором неизвестное содержится только в показателе степени при постоянных основаниях.
Простейшим показательным уравнением является уравнение вида
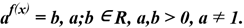
Это уравнение равносильно алгебраическому уравнению

Пример 1. Решить уравнение
 .
.
Представим правую часть уравнения в виде степени с основанием 2:
 .
.
Перейдем теперь к равносильному алгебраическому уравнению:

Если после введения новой переменной  показательное уравнение сводится к алгебраическому, дробно-рациональному или другому уравнению от переменной y, то сначала находят корни этого уравнения, а потом выражают x через y, используя решение простейшего показательного уравнения.
показательное уравнение сводится к алгебраическому, дробно-рациональному или другому уравнению от переменной y, то сначала находят корни этого уравнения, а потом выражают x через y, используя решение простейшего показательного уравнения.
Показательные неравенства
Показательными называются неравенства, в которых неизвестное содержится в показателе степени.
При решении показательных неравенств используются следующие утверждения:
A.1. Если a > 1, неравенство
a f (x) > a g (x)
равносильно неравенству
f (x) > g (x).
Аналогично, a f (x) < a g (x); f (x) < g (x).
A.2. Если 0 < a < 1, неравенство
a f (x) > a g (x)
равносильно неравенству
f (x) < g (x).
Аналогично, a f (x) < a g (x); f (x) > g (x).
A.3. Неравенство
| [ h (x)] f (x) > [ h (x)] g (x)
| (1)
|
равносильно совокупности систем неравенств
| 
| 
| h (x) > 1,
|
| f (x) > g (x),
|
| 
| 0 < h (x) < 1,
|
| f (x) < g (x).
|
Замечание.. Если знак неравенства (1) нестрогий, дополнительно рассматривается и случай
| 
| h (x) = 1,
|
| x D (f); D (g),
|
где D (f) (D (g)) означает область определения функции f (g).
A.4. Если b ≥ 0, неравенство
af (x) < b
не имеет решений (следует из свойств показательной функции).
A.5. Если b ≤ 0, множеством решений неравенства af (x) > b является x  D (f).
D (f).
A.6. Если a > 1, b > 0, неравенство
af (x) > b
равносильно неравенству
f (x) > log ab.
Аналогично, a f (x) < b; f (x) < log ab.
A.7. Если 0 < a < 1, b > 0, неравенство
a f (x) > b
равносильно неравенству
f (x) < log ab.
Аналогично, a f (x) < b; f (x) > log ab.
Упражнение 1. Решить неравенства:
| a) 
| |
| b) (0.3)|2 x -3| < (0.3)|3 x +4|,
| |
| c) 
| |
| |
Решение. a) Так как 2 > 1, используя утверждение A.1, получаем равносильное неравенство

которое решается методом интервалов,


b) Так как 0 < 0.3 < 1 используя утверждение A.2, получаем равносильное неравенство
|2 x -3| > |3 x +4|,
которое решается, используя свойства модуля (| a | > | b | (a - b)(a + b) > 0):
|2 x -3| > |3 x +4|  ((2 x -3)-(3 x +4)) ((2 x -3)+(3 x +4)) > 0
((2 x -3)-(3 x +4)) ((2 x -3)+(3 x +4)) > 0 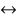 (- x -7)(5 x +1) > 0
(- x -7)(5 x +1) > 0
Решив последнее неравенство методом интервалов, получим x  (-7;-1/5).
(-7;-1/5).
c) Используя утверждение A.3, получим
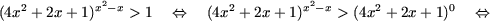
| 
| 
| 4 x 2+2 x +1 > 1,
| | x 2- x > 0,
| | 
| 4 x 2+2 x +1 < 1,
| | 4 x 2+2 x +1 > 0,
| | x 2- x < 0
| | | 
| 
| 
| x > 0,
| | x < -12,
| | 
| x > 1,
| | x < 0,
| | 
| | x  (-12;0), (-12;0),
| | x  R, R,
| | x  (0;1). (0;1).
| | |
Заключение
Математика, как и любая другая наука не стоит на месте, вместе с развитием общества меняются и взгляды людей, возникают новые мысли и идеи. И XX век не стал в этом смысле исключением. Появление компьютеров внесло свои корректировки в способы решения уравнений и значительно их облегчило. Но компьютер не всегда может быть под рукой (экзамен, контрольная), поэтому знание хотя бы самых главных способов решения уравнений необходимо знать. Использование уравнений в повседневной жизни – редкость. Они нашли свое применение во многих отраслях хозяйства и практически во всех новейших технологиях.
Список литературы
1. Курош А.Г. «Курс высшей алгебры» Москва 1975
2. Штейн Е.А. «Большая школьная энциклопедия» том 1; Москва 2004
3. М. Д. Аксенова. «Энциклопедия для детей». Том 11. Математика. – Аванта+, 1998.
4. Цыпкин А. Г. Под ред. С. А. Степанова. «Справочник по математике для средней школы». – М.: Наука, 1980
5. Г. Корн и Т. Корн. «Справочник по математике для научных работников и инженеров». – М.: Наука, 1970



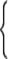







 или
или  или log2 x = log63. Следовательно,
или log2 x = log63. Следовательно, 

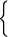


 (-8;-2]
(-8;-2] 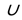 [4;+∞).
[4;+∞).

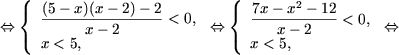
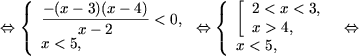
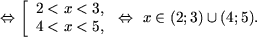
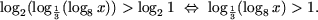
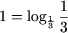 и, используя утверждение 2, получим
и, используя утверждение 2, получим
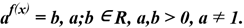

 .
. .
.
 показательное уравнение сводится к алгебраическому, дробно-рациональному или другому уравнению от переменной y, то сначала находят корни этого уравнения, а потом выражают x через y, используя решение простейшего показательного уравнения.
показательное уравнение сводится к алгебраическому, дробно-рациональному или другому уравнению от переменной y, то сначала находят корни этого уравнения, а потом выражают x через y, используя решение простейшего показательного уравнения.
 D (f).
D (f).




 ((2 x -3)-(3 x +4)) ((2 x -3)+(3 x +4)) > 0
((2 x -3)-(3 x +4)) ((2 x -3)+(3 x +4)) > 0 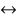 (- x -7)(5 x +1) > 0
(- x -7)(5 x +1) > 0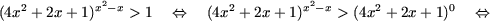

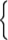





 (-12;0),
(-12;0), (-
(-  ; -12) (1;+
; -12) (1;+  ),
),
 x (-
x (-  ;- 12)
;- 12) 


