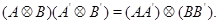Пусть  – группа и
– группа и  – ее подгруппа. Обозначим через
– ее подгруппа. Обозначим через  и
и  порядки групп
порядки групп  и
и 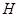 соответственно. Если
соответственно. Если  – некоторая функция на
– некоторая функция на  , то через
, то через  обозначим ее ограничение на
обозначим ее ограничение на 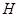 . В случае когда
. В случае когда  – функция классов на
– функция классов на  ,
,  также является функцией классов на
также является функцией классов на  . Если
. Если  – характер некоторого представления
– характер некоторого представления  группы
группы  , то
, то  представляет собой характер ограничения
представляет собой характер ограничения  представления
представления  на
на  .
.
По функции  , заданной на
, заданной на 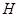 , определим функцию
, определим функцию  на
на  правилом
правилом

полагая  для
для  , не принадлежащих
, не принадлежащих  . Отметим, что
. Отметим, что  является функцией классов на
является функцией классов на  , даже еслм
, даже еслм  не является функцией классов на
не является функцией классов на  . Если
. Если  не сопряжен ни с каким элементом из
не сопряжен ни с каким элементом из 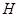 , то
, то  .
.
Лемма 5.1. Пусть  – функция классов на группе
– функция классов на группе  , а
, а 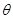 – функция классов на подгруппе
– функция классов на подгруппе 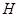 группы
группы  . Тогда
. Тогда

Доказательство. Имеем

Вклад в сумму дают лишь такие пары  , что
, что  . Поэтому, суммируя по тем парам
. Поэтому, суммируя по тем парам  , для которых
, для которых  при некотором
при некотором 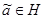 , получаем
, получаем



Если 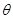 – характер некоторого представления группы
– характер некоторого представления группы  , то назовем
, то назовем  индуцированным характером группы
индуцированным характером группы  и скажем, что
и скажем, что 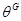 индуцирован с
индуцирован с  . Мы хотим показать, что каждый индуцированный характер действительно является характером некоторого представления группы
. Мы хотим показать, что каждый индуцированный характер действительно является характером некоторого представления группы  .
.
Пусть 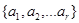 – множество представителей левых смежных классов группы
– множество представителей левых смежных классов группы  по
по 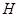 :
:

Для представления  подгруппы
подгруппы  определим матрицу
определим матрицу  так:
так:

где для  , не содержащихся в
, не содержащихся в 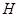 , полагаем
, полагаем  . Это обобщение правого регулярного представления группы
. Это обобщение правого регулярного представления группы  . Мы покажем, что
. Мы покажем, что

– представление группы  степени
степени  , где
, где  , а
, а  – степень
– степень  . При фиксированных
. При фиксированных 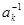 и
и  множество
множество  содержит по одному представителю из каждого левого смежного класса по
содержит по одному представителю из каждого левого смежного класса по  , поэтому среди матриц
, поэтому среди матриц  , лишь одна ненулевая. Аналогично, множество
, лишь одна ненулевая. Аналогично, множество  содержит по одному представителю из каждого правого смежного класса по
содержит по одному представителю из каждого правого смежного класса по  и среди матриц
и среди матриц  , также лишь одна ненулевая. Обозначим
, также лишь одна ненулевая. Обозначим  -й блок матрицы
-й блок матрицы  через
через  . Тогда
. Тогда

Покажем, что  . Имеется единственное число
. Имеется единственное число  , такое, что
, такое, что  , и единственное число
, и единственное число  , такое, что
, такое, что  . Если
. Если  , то
, то  . Если же
. Если же 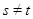 , то
, то  и
и  , поскольку
, поскольку  . В любом случае
. В любом случае  и следовательно,
и следовательно,  . Поскольку
. Поскольку  , матрица
, матрица  невырожденна. Таким образом
невырожденна. Таким образом  является представлением группы
является представлением группы  .
.
Пусть  – характер
– характер  , а
, а  – характер
– характер 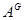 . Тогда
. Тогда


Тем самым мы получим  . Назовем
. Назовем  индуцированным представлением группы
индуцированным представлением группы  и будем говорить, что
и будем говорить, что  индуцировано с
индуцировано с  . Сказанное суммирует следующая
. Сказанное суммирует следующая
Теорема 5.2. Пусть  – группа и
– группа и 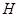 – ее подгруппа. Пусть
– ее подгруппа. Пусть  – представление
– представление  степени
степени  , а
, а 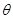 – его характер. Тогда индуцированное представление
– его характер. Тогда индуцированное представление  имеет степень
имеет степень  , где
, где  , и характер
, и характер

Теорема 5.3. (Закон взаимности Фробениуса.) Пусть  – подгруппа в
– подгруппа в  . Пусть
. Пусть  – полный набор неприводимых характеров группы
– полный набор неприводимых характеров группы  , а
, а  – полный набор неприводимых характеров группы
– полный набор неприводимых характеров группы  . Тогда
. Тогда
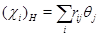
в том и только том случае, когда

Другими словами, если  – неприводимое представление группы
– неприводимое представление группы  , а
, а  – неприводимое представление
– неприводимое представление 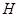 , то
, то  является неприводимой компонентой в
является неприводимой компонентой в 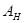 кратности
кратности  тогда и только тогда, когда
тогда и только тогда, когда  является неприводимой компонентой в
является неприводимой компонентой в  кратности
кратности  .
.
Доказательство. Пусть  и
и  . В силу леммы 5.1
. В силу леммы 5.1

Произведение представлений
Пусть  – квадратные матрицы порядков
– квадратные матрицы порядков  и
и  соответственно, и пусть
соответственно, и пусть  . Определим кронекерово, или тензорное, произведение
. Определим кронекерово, или тензорное, произведение  матриц
матриц  и
и  следующим образом:
следующим образом:

Значит,  представляет собой квадратную матрицу порядка
представляет собой квадратную матрицу порядка  . Непосредственными вычислениями устанавливается следующая
. Непосредственными вычислениями устанавливается следующая
Лемма 6.1.
(1)  ,
,
(2) если  имеют степень
имеют степень  , a
, a  – степень
– степень  , то
, то 
Пусть  и
и  – представления группы
– представления группы  . Тогда в силу леммы 6.1 (2) отображение
. Тогда в силу леммы 6.1 (2) отображение

также является представлением этой группы. Такое представление называют произведением представлений  и обозначают через
и обозначают через  . Пусть
. Пусть 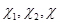 – характеры представлений
– характеры представлений  соответственно. По лемме 6.1 (1)
соответственно. По лемме 6.1 (1)

Пусть  – полный набор неприводимых представлений группы
– полный набор неприводимых представлений группы  , а
, а  – характер
– характер  . Отображение
. Отображение  также является неприводимым, и его характер – это
также является неприводимым, и его характер – это  , где
, где  . Пусть
. Пусть  .
.
Теорема 6.2. Равенство

имеет место тогда и только тогда, когда

Доказательство.


Таким образом, кратность вхождения 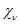 в
в 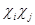 равна кратности вхождения
равна кратности вхождения  в
в 
Теорема 6.3. Пусть  – точное представление группы
– точное представление группы  и
и 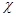 – его характер. Пусть
– его характер. Пусть  – число различных значений, которые принимает
– число различных значений, которые принимает 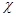 на
на  . Тогда каждое неприводимое представление группы
. Тогда каждое неприводимое представление группы  входит в
входит в
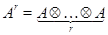
для некоторого  , где
, где  .
.
Доказательство. Предположим, что неприводимое представление  не входит в
не входит в  . Пусть
. Пусть  – характеры
– характеры  и
и  соответственно. Тогда
соответственно. Тогда

для 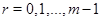 . Пусть
. Пусть  принимает на
принимает на  значение
значение  . Положим
. Положим 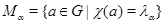 и
и  . В силу (6.1)
. В силу (6.1)

для  Рассмотрим (6.2) как систему линейных уравнений для
Рассмотрим (6.2) как систему линейных уравнений для  . Поскольку
. Поскольку 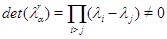 , эта система имеет решение
, эта система имеет решение 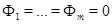 .
.
Пусть  – степень представления
– степень представления  , т.е.
, т.е.  . Мы можем считать, что
. Мы можем считать, что  . Покажем, что
. Покажем, что  . Пусть
. Пусть  , т.е.
, т.е.  . Обозначим через
. Обозначим через  циклическую группу, порожденную элементом
циклическую группу, порожденную элементом  . По теореме 3.3
. По теореме 3.3  эквивалентно прямой сумме представлений степени 1. Значит, для некоторой невырожденной матрицы
эквивалентно прямой сумме представлений степени 1. Значит, для некоторой невырожденной матрицы 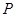

Пусть  – порядок элемента
– порядок элемента  . Тогда
. Тогда  . Взяв след в равенстве (6.3), получаем
. Взяв след в равенстве (6.3), получаем 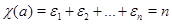 . Это означает, что
. Это означает, что 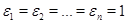 , т.е.
, т.е.  . Плскольку
. Плскольку  точно,
точно,  . Поэтому
. Поэтому  и
и  . Полученное противоречие доказывает теорему.
. Полученное противоречие доказывает теорему. 
Таблицы характеров. Пусть  – группа и
– группа и  – классы сопряженных элементов в
– классы сопряженных элементов в  . Пусть
. Пусть 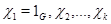 – нерпиводимые характеры группы
– нерпиводимые характеры группы  , а
, а  – представители ее классов сопряженных элементов. Отметим, что в силу теоремы 4.10 число неприводимых характеров совпадает с числом классов сопряженности. Упорядочим значения
– представители ее классов сопряженных элементов. Отметим, что в силу теоремы 4.10 число неприводимых характеров совпадает с числом классов сопряженности. Упорядочим значения  таким образом, чтобы получить таблицу характеров группы
таким образом, чтобы получить таблицу характеров группы  , в которой строки помечены различными неприводимыми характерами, начиная с
, в которой строки помечены различными неприводимыми характерами, начиная с  , а столбцы – классами сопряженности группы
, а столбцы – классами сопряженности группы  , начиная с класса
, начиная с класса  .
.
Различные строки таблицы характеров ортогональны между собой в смысле теоремы  , а в силу теоремы 4.9 столбцы ортогональны между собой в обычном смысле как векторы комплексного унитарного пространства.
, а в силу теоремы 4.9 столбцы ортогональны между собой в обычном смысле как векторы комплексного унитарного пространства.
Заключение
Таким образом, в данной работе мы показали, что каждое представление конечной группы эквивалентно некоторому ее унитарному представлению и является мполне приводимым.
Путем прямых вычислений доказали лемму:

 для произвольной квадратной матрицы
для произвольной квадратной матрицы 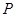 и теорему: Пусть
и теорему: Пусть  – группа и
– группа и  – ее подгруппа. Пусть
– ее подгруппа. Пусть  – представление
– представление  степени
степени  , а
, а  – его характер. Тогда индуцированное представление
– его характер. Тогда индуцированное представление  имеет степень
имеет степень  , где
, где  , и характер
, и характер

Непосредственными вычислениями была устанавлена следующая лемма:  ,
,
(2) если  имеют степень
имеют степень  , a
, a  – степень
– степень  , то
, то 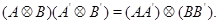
Список использованных источников
Сыскин С.А. Абстрактные свойства простых спорадических групп. – Усп. мат. наук, 1980, т. 35, №5, (215), с. 181–212.
Монахов В.С. О трижды факторизуемых группах. – Изв. АН БССР. Сер. физ.-мат. наук, 1981, №6, с. 18–23.
Монахов В.С. Произведение разрешимой и циклической групп // Сб. VI всес. симпозиум по теории групп.-Киев: Наукова думка, 1980-с. 189–195
Монахов В.С. О произведении двух групп с циклическими подгруппами индекса 2 // Весцi АН Беларусi. сер. фiз.-мат. навук. – 1996, №3-с. 21–24


 – группа и
– группа и  – ее подгруппа. Обозначим через
– ее подгруппа. Обозначим через 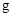 и
и  порядки групп
порядки групп  и
и 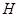 соответственно. Если
соответственно. Если  – некоторая функция на
– некоторая функция на  обозначим ее ограничение на
обозначим ее ограничение на  – функция классов на
– функция классов на  ,
,  также является функцией классов на
также является функцией классов на  . Если
. Если  – характер некоторого представления
– характер некоторого представления  группы
группы  , то
, то  представляет собой характер ограничения
представляет собой характер ограничения  представления
представления  .
. , заданной на
, заданной на  на
на  правилом
правилом
 для
для  , не принадлежащих
, не принадлежащих  . Отметим, что
. Отметим, что  , даже еслм
, даже еслм  не является функцией классов на
не является функцией классов на  не сопряжен ни с каким элементом из
не сопряжен ни с каким элементом из  .
.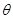 – функция классов на подгруппе
– функция классов на подгруппе 

 , что
, что  . Поэтому, суммируя по тем парам
. Поэтому, суммируя по тем парам  , для которых
, для которых  при некотором
при некотором 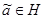 , получаем
, получаем


 , то назовем
, то назовем  и скажем, что
и скажем, что 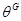 индуцирован с
индуцирован с  . Мы хотим показать, что каждый индуцированный характер действительно является характером некоторого представления группы
. Мы хотим показать, что каждый индуцированный характер действительно является характером некоторого представления группы 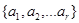 – множество представителей левых смежных классов группы
– множество представителей левых смежных классов группы  по
по 
 подгруппы
подгруппы  так:
так:
 , не содержащихся в
, не содержащихся в  . Это обобщение правого регулярного представления группы
. Это обобщение правого регулярного представления группы 
 степени
степени  , где
, где  , а
, а  – степень
– степень 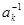 и
и  множество
множество  содержит по одному представителю из каждого левого смежного класса по
содержит по одному представителю из каждого левого смежного класса по  , лишь одна ненулевая. Аналогично, множество
, лишь одна ненулевая. Аналогично, множество  содержит по одному представителю из каждого правого смежного класса по
содержит по одному представителю из каждого правого смежного класса по  , также лишь одна ненулевая. Обозначим
, также лишь одна ненулевая. Обозначим  -й блок матрицы
-й блок матрицы  через
через  . Тогда
. Тогда
 . Имеется единственное число
. Имеется единственное число  , такое, что
, такое, что  , и единственное число
, и единственное число  , такое, что
, такое, что  . Если
. Если  , то
, то  . Если же
. Если же 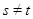 , то
, то  и
и  , поскольку
, поскольку  . В любом случае
. В любом случае  и следовательно,
и следовательно,  . Поскольку
. Поскольку  , матрица
, матрица  невырожденна. Таким образом
невырожденна. Таким образом  является представлением группы
является представлением группы  .
. , а
, а  – характер
– характер 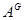 . Тогда
. Тогда

 . Назовем
. Назовем  индуцированным представлением группы
индуцированным представлением группы  , а
, а  , где
, где  , и характер
, и характер
 – полный набор неприводимых характеров группы
– полный набор неприводимых характеров группы  – полный набор неприводимых характеров группы
– полный набор неприводимых характеров группы 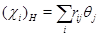

 , а
, а  – неприводимое представление
– неприводимое представление  является неприводимой компонентой в
является неприводимой компонентой в 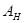 кратности
кратности  тогда и только тогда, когда
тогда и только тогда, когда  кратности
кратности  .
. и
и  . В силу леммы 5.1
. В силу леммы 5.1
 – квадратные матрицы порядков
– квадратные матрицы порядков  и
и  соответственно, и пусть
соответственно, и пусть  . Определим кронекерово, или тензорное, произведение
. Определим кронекерово, или тензорное, произведение  матриц
матриц 
 представляет собой квадратную матрицу порядка
представляет собой квадратную матрицу порядка  . Непосредственными вычислениями устанавливается следующая
. Непосредственными вычислениями устанавливается следующая ,
, имеют степень
имеют степень  , a
, a  – степень
– степень  , то
, то 
 и
и  – представления группы
– представления группы 
 и обозначают через
и обозначают через  . Пусть
. Пусть 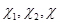 – характеры представлений
– характеры представлений  соответственно. По лемме 6.1 (1)
соответственно. По лемме 6.1 (1)
 – полный набор неприводимых представлений группы
– полный набор неприводимых представлений группы  – характер
– характер  . Отображение
. Отображение  также является неприводимым, и его характер – это
также является неприводимым, и его характер – это  , где
, где  . Пусть
. Пусть  .
.



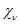 в
в 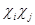 равна кратности вхождения
равна кратности вхождения  в
в 
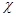 – его характер. Пусть
– его характер. Пусть  . Тогда каждое неприводимое представление группы
. Тогда каждое неприводимое представление группы  входит в
входит в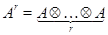
 , где
, где  .
. . Пусть
. Пусть  – характеры
– характеры  соответственно. Тогда
соответственно. Тогда
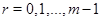 . Пусть
. Пусть  . Положим
. Положим 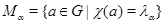 и
и  . В силу (6.1)
. В силу (6.1)
 Рассмотрим (6.2) как систему линейных уравнений для
Рассмотрим (6.2) как систему линейных уравнений для  . Поскольку
. Поскольку 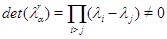 , эта система имеет решение
, эта система имеет решение 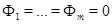 .
. . Мы можем считать, что
. Мы можем считать, что  . Покажем, что
. Покажем, что  . Пусть
. Пусть  , т.е.
, т.е.  . Обозначим через
. Обозначим через  циклическую группу, порожденную элементом
циклическую группу, порожденную элементом  . По теореме 3.3
. По теореме 3.3  эквивалентно прямой сумме представлений степени 1. Значит, для некоторой невырожденной матрицы
эквивалентно прямой сумме представлений степени 1. Значит, для некоторой невырожденной матрицы 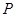

 – порядок элемента
– порядок элемента  . Тогда
. Тогда  . Взяв след в равенстве (6.3), получаем
. Взяв след в равенстве (6.3), получаем 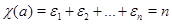 . Это означает, что
. Это означает, что 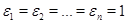 , т.е.
, т.е.  . Плскольку
. Плскольку  . Поэтому
. Поэтому  . Полученное противоречие доказывает теорему.
. Полученное противоречие доказывает теорему. 
 – классы сопряженных элементов в
– классы сопряженных элементов в 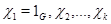 – нерпиводимые характеры группы
– нерпиводимые характеры группы  – представители ее классов сопряженных элементов. Отметим, что в силу теоремы 4.10 число неприводимых характеров совпадает с числом классов сопряженности. Упорядочим значения
– представители ее классов сопряженных элементов. Отметим, что в силу теоремы 4.10 число неприводимых характеров совпадает с числом классов сопряженности. Упорядочим значения  таким образом, чтобы получить таблицу характеров группы
таким образом, чтобы получить таблицу характеров группы  , в которой строки помечены различными неприводимыми характерами, начиная с
, в которой строки помечены различными неприводимыми характерами, начиная с  , а столбцы – классами сопряженности группы
, а столбцы – классами сопряженности группы  .
. , а в силу теоремы 4.9 столбцы ортогональны между собой в обычном смысле как векторы комплексного унитарного пространства.
, а в силу теоремы 4.9 столбцы ортогональны между собой в обычном смысле как векторы комплексного унитарного пространства.
 для произвольной квадратной матрицы
для произвольной квадратной матрицы  – группа и
– группа и  – ее подгруппа. Пусть
– ее подгруппа. Пусть  степени
степени  , а
, а  – его характер. Тогда индуцированное представление
– его характер. Тогда индуцированное представление  имеет степень
имеет степень  , где
, где  , и характер
, и характер ,
, имеют степень
имеют степень  – степень
– степень  , то
, то