Теория подобия предлагает проводить обработку опытных данных, используя обобщенные переменные (безразмерные комплексы, составленные из переменных, влияющих на данный процесс). При этом снижается число переменных (облегчается обработка опытных данных) и расширяются условия применимости полученных эмпирических уравнений (эти уравнения можно использовать не только для исследуемого экспериментального процесса, но и для процессов, подобных исследуемому). Например, известно, что на режим движения жидкости влияют средняя скорость υ, эквивалентный диаметр d э, плотность ρ, коэффициент динамической вязкости μ. Однако влияние этих четырех параметров можно оценить, используя одну обобщенную переменную – критерий Рейнольдса:

Применяя теорию подобия, можно проводить изучение сложных процессов на моделях (чаще всего – на лабораторных установках), а полученные эмпирические уравнения использовать для расчета подобных промышленных процессов и аппаратов.
Существует несколько видов гидродинамического подобия – геометрическое, кинематическое и динамическое. Геометрическое подобие предполагает пропорциональность сходственных геометрических параметров. Кинематическое подобие означает пропорциональность местных скоростей в сходственных точках и равенство углов, характеризующих направления векторов скоростей. Из кинематического подобия вытекает геометрическое подобие линий тока (то есть для кинематического подобия требуется соблюдение и геометрического подобия). Динамическое подобие предполагает пропорциональность сил, действующих на сходственные объемы в кинематически подобных потоках и равенство углов, характеризующих направление этих сил.
Рассмотрим наиболее простой вид подобия – геометрическое. Пусть сечение двух геометрически подобных потоков имеет треугольную форму (рис. 23). Условие геометрического подобия:  , где K ℓ – константа подобия линейных размеров.
, где K ℓ – константа подобия линейных размеров.

Рис. 23. Пример геометрического подобия
Условие геометрического подобия можно записать и так:
 , где i ℓ - инвариант геометрического подобия.
, где i ℓ - инвариант геометрического подобия.
Инвариант, составленный из однородных величин, называют симплексом подобия. Например:  (здесь ℓ – длина прямого участка трубы, d – внутренний диаметр трубы).
(здесь ℓ – длина прямого участка трубы, d – внутренний диаметр трубы).
Инвариант, составленный из разнородных величин, называется критерием подобия. Например:
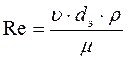
Критерии подобия – обобщенные переменные (безразмерные комплексы, определенным образом составленные из разнородных величин). Установить вид критериев подобия, определяющих ход изучаемого процесса, можно путем преобразования дифференциального уравнения процесса. Если такового не имеется, можно использовать более формальный подход (например, метод анализа размерностей).
Критерии гидродинамического подобия. Течение вязких несжимаемых жидкостей описывается системой дифференциальных уравнений Навье-Стокса. Используем одно из уравнений в проекции на ось z. Считаем, что на жидкость из массовых сил действуют только силы тяжести (Z = - g):

Поскольку υz = υz(x,y,z,t), уравнение в развернутой форме принимает следующий вид:
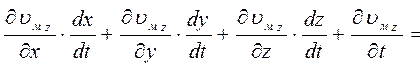

где  ;
;  ;
; 
При выводе уравнений Навье-Стокса было отмечено, что первый член правой части уравнения учитывает влияние сил тяжести, второй член – влияние сил давления, третий член – влияние сил вязкого трения. Левая часть уравнения учитывает влияние сил инерции.
Преобразуем уравнение методом, предложенным в теории подобия. Для этого используем следующие правила:
1. Рассматриваются и анализируются только величины, обладающие размерностью.
2. Знаки дифференциалов отбрасываются (дифференциалы заменяются конечными величинами). Полученные таким образом выражения записываются в виде соотношений пропорциональности.
В случае преобразования уравнений, в которые входят производные не первого, а более высокого порядка (в частности, второго), при отбрасывании знаков дифференциалов соблюдается следующее правило:  ~
~  , и т.п.
, и т.п.
При этом пространственные координаты x, y, z могут быть заменены на некоторый характерный линейный размер ℓ.
Поскольку критерии подобия – безразмерные обобщенные переменные, их можно получить делением одного из членов уравнения на другой. Перед этим предварительно проведем преобразование уравнений Навье-Стокса, умножая на ρ все члены уравнения и группируя левую часть уравнения, что дает следующий результат:
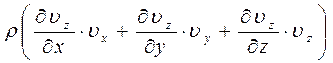 ~
~ 
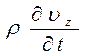 ~
~ 
Аналогично преобразуем правую часть уравнения:
-ρ g ~ ρ g
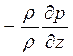 ~
~ 
 ~
~ 
Здесь величина, пропорциональная давлению p, заменяется на разность давлений ∆p - величину с той же размерностью, что и давление, но имеющую особое прикладное значение в гидравлике. Преобразованные члены уравнения следует поделить на один из них (рассматривая его в качестве масштаба). Для этого обычно используют член, выражающий влияние сил инерции - 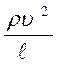 :
:
 ;
;
 (критерий Фруда)
(критерий Фруда)
Физический смысл критерия Фруда состоит в том, что он отражает влияние сил тяжести на движение жидкости (является мерой отношения сил инерции к силам тяжести).
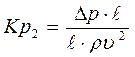 ;
;
 (критерий Эйлера)
(критерий Эйлера)
Критерий Эйлера является мерой отношения сил давления к силам инерции в потоке вязкой жидкости.
 ;
;
 (критерий Рейнольдса)
(критерий Рейнольдса)
Критерий Рейнольдса выражает меру отношения сил инерции к силам вязкого трения при движении жидкости.
 ;
;
 (критерий гомохронности)
(критерий гомохронности)
Критерий гомохронности является критерием временного подобия и используется для описания неустановившихся процессов движения жидкостей.
Теоремы подобия
1. В подобных процессах сходственные критерии подобия численно равны.
2. Решение любого дифференциального уравнения можно представить в виде зависимости между критериями подобия, характерными для данного процесса.
3. Процессы подобны, если их сходственные определяющие критерии подобия численно равны.
Определяющие критерии – такие, в состав которых входят независимые переменные, определяющие ход процесса. В состав определяемых критериев входят искомые функции.
Условия гидродинамического подобия
Согласно первой теореме подобия, условия гидродинамического подобия запишутся:
Fr = idem
Re = idem
Ho = idem Термин “idem” означает «одно и то же».
Eu = idem
Критериальное уравнение движения вязкой жидкости.
Согласно второй теореме подобия, критериальное уравнение движения вязкой жидкости должно иметь вид:
f (Eu, Fr, Re, Ho, Г1, Г2, Г3,…) = 0
Здесь Г1, Г2, Г3,… - симплексы геометрического подобия.
Чаще всего при решении гидравлических задач определяемым является критерий Эйлера, все остальные критерии и симплексы подобия являются определяющими. Отсюда
Eu = f (Fr, Re, Ho, Г1, Г2, Г3,…)
Рассмотрим некоторые частные случаи использования данного критериального уравнения. В случае установившегося движения жидкости критерий гомохронности следует исключить из данного уравнения. Если к тому же рассматривается установившееся напорное движение вязкой жидкости, из критериального уравнения следует также исключить критерий Фруда, который учитывает влияние сил тяжести на движение потока вязкой жидкости. При напорном движении потока основной движущей силой является перепад давлений, влияние сил тяжести незначительно. Отсюда
Eu = f (Re, Г1, Г2, Г3,…)
Третья теорема подобия определяет границы применимости критериальных уравнений, полученных эмпирическим путем (они справедливы в тех же пределах, в которых изменялись определяющие критерии подобия).
1.18. Потери напора по длине потока.
Формула Дарси-Вейсбаха
Используем критериальное уравнение установившегося напорного движения (случай, наиболее часто встречающийся в промышленной практике):
Eu = f (Re, Г1, Г2, Г3,…)
Для составления симплексов геометрического подобия необходимо установить, какие геометрические параметры влияют на величину потерь напора. Поскольку причиной потерь энергии является трение слоев жидкости друг о друга и о стенки трубы, такими параметрами являются длина участка трубы, ее внутренний диаметр, шероховатость стенки (l, d, ∆ соответственно, где ∆ - более точно - абсолютная шероховатость стенки трубопровода, т.е. средняя высота микронеровностей на ее поверхности).
Из этих трех параметров можно составить два симплекса подобия:
 ;
;  , где ε - относительная шероховатость.
, где ε - относительная шероховатость.
Составим уравнение Бернулли для двух сечений горизонтального потока в прямой трубе (d1 = d2). Плоскость сравнения 0 - 0 проведем по оси трубопровода (рис. 24):


Рис. 24. Иллюстрация к составлению уравнения Бернулли для двух сечений горизонтального потока в прямой трубе
Здесь υ 1 = υ 2 (в соответствии с уравнением неразрывности потока), ∆ h ℓ – потери напора по длине потока, коэффициент Кориолиса α близок к единице для турбулентных потоков, поэтому его обычно не учитывают.
Из уравнения Бернулли определяем ∆ h ℓ:

Конкретизируем вид критериального уравнения при движении потока вязкой жидкости в прямой горизонтальной трубе:
То есть 

Решаем уравнение относительно ∆ p ℓ, имея в виду тот экспериментальный факт, что потери давления ∆ p ℓ пропорциональны
 симплексу
симплексу  :
:
2 f (Re, ε) обозначим как λ – коэффициент сопротивления по длине потока (коэффициент гидравлического трения).
Поскольку 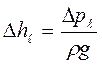 , получаем формулу Дарси – Вейсбаха:
, получаем формулу Дарси – Вейсбаха:

Таким образом, в соответствии с формулой Дарси-Вейсбаха потери напора по длине потока прямо пропорциональны длине прямого участка, скоростному напору и обратно пропорциональны внутреннему диаметру трубопровода.
1.19. Потери напора по длине ламинарного потока
Явный вид функции λ = f (Re, ε) может быть получен в общем случае только с помощью эксперимента, однако для ламинарного потока в прямой горизонтальной трубе существует теоретическое решение.

Рис. 25. Структурно-динамическая схема
ламинарного потока
Рассмотрим равномерное ламинарное стабилизированное (со сформировавшимся профилем скоростей) движение вязкой жидкости в прямой горизонтальной трубе (рис. 25). Составим уравнение Бернулли для двух сечений (1 - 1 и 2 - 2 на схеме выше) с коэффициентом Кориолиса для ламинарного потока, равным 2:

Здесь средние скорости υ 1 = υ 2 (поскольку d 1 = d 2 = d). Отсюда
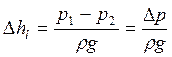
Выделим в потоке цилиндрический элемент радиуса r с длиной образующей ℓ. Поскольку данный элемент жидкости движется равномерно и прямолинейно, из курса механики известно, что в этом случае сумма сил, действующих на тело, равна нулю. Рассмотрим соответствующее уравнение в проекции на горизонтальную ось потока (в этом случае влияние силы тяжести можно не учитывать):
P – T = 0
где
P – результирующая сил давления: P = P 1 - P 2 = (р1 – р2)· S
T – результирующая сил вязкого трения: T = τ · S бок
Здесь силы трения действуют по боковой поверхности цилиндрического элемента и направлены встречно движению потока (тормозят это движение), и поскольку S = π r 2, S бок = 2 π r · ℓ, а
P – T = 0, то равенство P = T запишется так:

Откуда 
Из формулы следует, что касательное напряжение по сечению ламинарного потока является линейной функцией радиуса (расстояния от центра потока). Эпюра касательных напряжений представлена на вышерасположенной схеме слева.
Рассмотрим теперь распределение местных скоростей по сечению ламинарного потока. Запишем закон вязкого трения применительно к нашей схеме:

Знак «минус» поставлен потому, что скорость уменьшается с ростом радиуса, поэтому 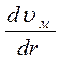 всегда отрицательно. Подставляем значение τ в предыдущее выражение:
всегда отрицательно. Подставляем значение τ в предыдущее выражение:
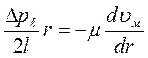
Разделяем переменные и интегрируем:


Постоянную С найдем из граничного условия: υм = 0 при r = R
(R - радиус трубы)

Подставляем С и находим закон изменения местных скоростей по сечению потока:
 - закон Стокса
- закон Стокса
Из уравнения видно, что скорость по сечению потока является параболической функцией радиуса (расстояния от центра потока). Эпюра скоростей представлена на вышерасположенной схеме справа.
Найдем максимальное значение скорости в центре потока – при r = 0:

Определим теперь расход через элементарное кольцевое сечение (радиус кольца r, ширина dr) из соотношения: dQ = υм · dS = υм ·2π r · dr,
т.е. 
Найдем расход потока, интегрируя полученное выражение в пределах изменения радиуса кольца от 0 до R:

 - уравнение Пуазейля
- уравнение Пуазейля
Найдем среднюю скорость по сечению S:


Из сравнения полученного выражения для средней скорости с максимальной скоростью для данного сечения получаем:
υ= 0,5·υм max
Определим потери давления с помощью уравнения Пуазейля:

Отсюда потери напора по длине ламинарного потока:
 (с учетом того, что μ/ ρ = ν)
(с учетом того, что μ/ ρ = ν)
Приведем полученное выражение к виду, характерному для уравнения Дарси-Вейсбаха, т.е.:

Для этого заменим 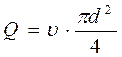 , умножим числитель и знаменатель на среднюю скорость υ, перегруппируем сомножители и получим:
, умножим числитель и знаменатель на среднюю скорость υ, перегруппируем сомножители и получим:

Сравнивая это выражение с формулой Дарси-Вейсбаха и учитывая, что 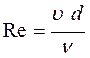 , для ламинарного потока имеем:
, для ламинарного потока имеем:

Изложенная теория ламинарного движения потока в круглой трубе хорошо согласуется с опытом, если речь идет о стабилизированном течении, когда сформировался параболический профиль распределения местных скоростей по сечению потока.






 , где K ℓ – константа подобия линейных размеров.
, где K ℓ – константа подобия линейных размеров.
 , где i ℓ - инвариант геометрического подобия.
, где i ℓ - инвариант геометрического подобия. (здесь ℓ – длина прямого участка трубы, d – внутренний диаметр трубы).
(здесь ℓ – длина прямого участка трубы, d – внутренний диаметр трубы).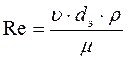

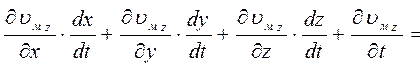

 ;
;  ;
; 
 ~
~  , и т.п.
, и т.п.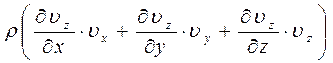 ~
~ 
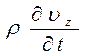 ~
~ 
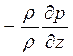 ~
~ 
 ~
~ 
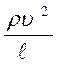 :
: ;
;  (критерий Фруда)
(критерий Фруда)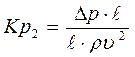 ;
;  (критерий Эйлера)
(критерий Эйлера) ;
;  (критерий Рейнольдса)
(критерий Рейнольдса) ;
;  (критерий гомохронности)
(критерий гомохронности) ;
;  , где ε - относительная шероховатость.
, где ε - относительная шероховатость.




 симплексу
симплексу  :
: 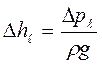 , получаем формулу Дарси – Вейсбаха:
, получаем формулу Дарси – Вейсбаха:


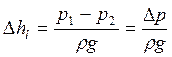



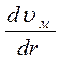 всегда отрицательно. Подставляем значение τ в предыдущее выражение:
всегда отрицательно. Подставляем значение τ в предыдущее выражение: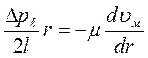



 - закон Стокса
- закон Стокса


 - уравнение Пуазейля
- уравнение Пуазейля


 (с учетом того, что μ/ ρ = ν)
(с учетом того, что μ/ ρ = ν)
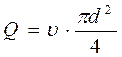 , умножим числитель и знаменатель на среднюю скорость υ, перегруппируем сомножители и получим:
, умножим числитель и знаменатель на среднюю скорость υ, перегруппируем сомножители и получим:
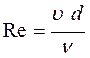 , для ламинарного потока имеем:
, для ламинарного потока имеем:


