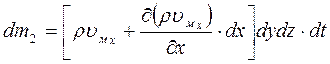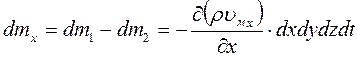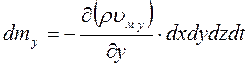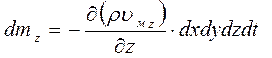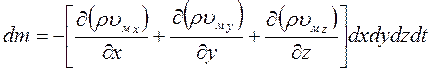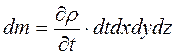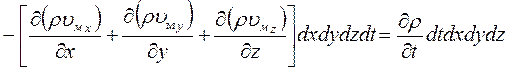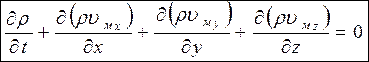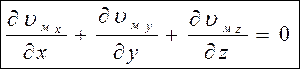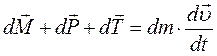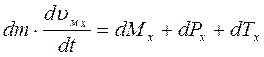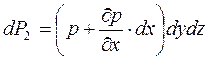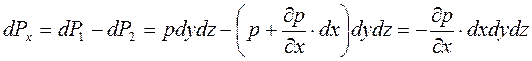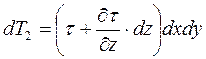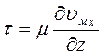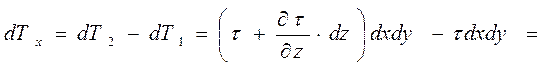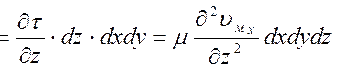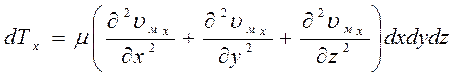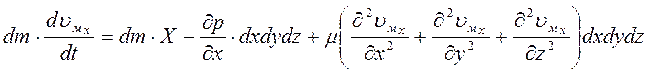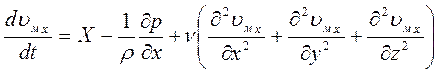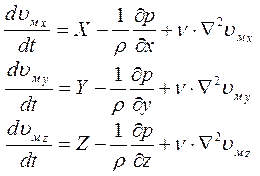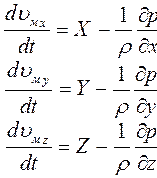Жидкость может двигаться или находиться в равновесии под действием приложенных внешних сил (внутреннее молекулярное движение в гидравлике в расчет не принимается). Поскольку жидкость обладает большой подвижностью частиц, она не способна сопротивляться действию сосредоточенных сил; силы должны быть распределены либо по поверхности жидкости, либо по ее массе (объему). Соответственно, различают два класса сил - поверхностные (пропорциональные площади поверхности жидкости) и массовые (пропорциональные массе жидкости). К поверхностным силам относятся силы давления и трения, к массовым - сила тяжести, центробежная сила, сила инерции. Поверхностные силы обусловлены непосредственным воздействием соседних объемов жидкости на данный объем или воздействием других тел (твердых или газообразных), граничащих с данной жидкостью. В общем случае поверхностная сила ΔFможет быть разложена на две составляющие- нормальную к площадке ΔS и тангенциальную (рис. 8). Первая – ΔP - является силой давления, вторая – ΔT - силой трения.
Поверхностная сила, отнесенная к единице поверхности, называется напряжением поверхностной силы. Нормальное напряжение (т.е. напряжение силы давления) называют гидродинамическим давлением или просто давлением. В общем случае:


А напряжение силы трения численно равно напряжению сдвига:

Рис. 8. Поверхностные силы,
действующие в жидкости (пояснения – в тексте).
ГЛАВА 2. Основные законы гидравлики
1.6. Уравнения расхода для элементарной струйки
И потока жидкости
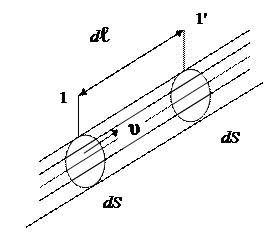 Пусть элементарная струйка имеет живое сечение dS и в данный момент времени занимает положение 1 (рис. 9). Через время dt сечение dS перемещается в направлении скорости υ и занимает новое положение 1' (все жидкие частицы в сечении dS имеют одинаковую скорость υ согласно струйной модели). За время dt сечение dS проходит путь, равный dl.
Пусть элементарная струйка имеет живое сечение dS и в данный момент времени занимает положение 1 (рис. 9). Через время dt сечение dS перемещается в направлении скорости υ и занимает новое положение 1' (все жидкие частицы в сечении dS имеют одинаковую скорость υ согласно струйной модели). За время dt сечение dS проходит путь, равный dl.
Определим расход жидкости
Рис. 9. Иллюстрация через сечение dS:
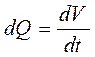 к выводу уравнения
к выводу уравнения
объемного расхода ,
где dV - объем жидкости, заключенный между положением 1 и 1'.
Поскольку объем цилиндрического тела dV = dS · d ℓ, то
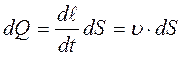
Таким образом получаем уравнение объемного расходадля элементарной струйки:
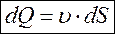
Согласно струйной модели, поток жидкости представляет собой совокупность множества элементарных струек, поэтому:
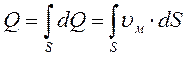
где υм - местные скорости в сечении S (скорости различных элементарных струек). Интеграл можно взять, если известен закон распределения местных скоростей по сечению потока. Этот закон теоретически определен только для ламинарного потока, поэтому в гидравлике при выводе общего выражения для Q используется упрощение – вводится средняя скорость по сечению потока, с помощью которой определяется уравнение расхода для потока жидкости:
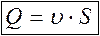
где 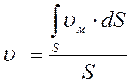 (см. раздел 1.23)
(см. раздел 1.23)
Таким образом, υ - это условная, постоянная для данного сечения (средняя) скорость потока, которая обеспечивает такой же расход, как и при реальном распределении скоростей. В гидравлических расчетах используют именно среднюю скорость, поскольку определение местных скоростей весьма затруднительно. Кроме того, для элементарной струйки можно считать υ м = υ ср ≡ υ.
1.7. Дифференциальные уравнения неразрывности. Уравнение неразрывности для потока
Несжимаемой жидкости
Уравнения неразрывности для элементарной струйки и одномерного потока жидкости.

Рис. 10. Иллюстрация к выводу уравнения неразрывности
для элементарной струйки
Выберем в элементарной струйке два сечения 1 и 2 (живые сечения dS 1 и dS 2) на конечном расстоянии друг от друга (рис. 10). Согласно струйной модели потока, параметры движущейся жидкости (скорость, плотность) изменяются только по одной координате (вдоль пути струйки, и тогда υ м = υ). Через время dt сечение 1 смещается в положение 1', а сечение 2 - в положение 2'. Тогда масса жидкости, вошедшей в объем между сечениями 1 и 2:
dm1 = dM1 · dt = ρ1 υ 1 · dS1· dt
а масса жидкости, вышедшей из объема между сечениями 1 и 2:
dm 2 = dM 2 · dt = ρ 2 υ 2 ∙ dS 2 · dt
Согласно закону сохранения массы, а также благодаря одному из свойств элементарной струйки (непроницаемости ее стенок) можно констатировать, что dm 1 = dm 2, откуда
ρ 1 υ 1 · dS 1 ∙ dt = ρ 2 υ 2 · dS 2 ∙ dt
После сокращения получаем уравнение неразрывности для элементарной струйки сжимаемой жидкости:
ρ 1 υ 1 · dS 1 = ρ 2 υ 2 · dS 2
Для несжимаемой жидкости ρ 1 = ρ 2 = const, поэтому
υ 1 · dS 1 = υ 2 · dS 2 (*)
Чтобы перейти к потоку жидкости, нужно проинтегрировать каждое из сечений по всем элементарным струйкам, проходящим через них. При этом необходимо помнить, что у каждой из струек скорость своя и единственная, хотя в рамках потока она одна из многих – т.е. местная (υ м). С учетом этого интегрируем левую часть уравнения (*) по площади S 1, а правую часть - по площади S 2:
∫ υ 1м · dS 1 = ∫ υ 2м · dS 2
s1 s2
И после перехода от местных к средним скоростям по потоку (т.е. по всем элементарным струйкам), которые представляют собой константы для каждого из сечений 1 и 2, и интегрирования по сечениям dS 1 и · dS 2, получаем уравнение неразрывности для одномерного потока несжимаемой жидкости:
υ 1 · S 1 = υ 2 · S 2
Его следствие: 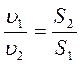 , т.е.
, т.е.
средние скорости обратно пропорциональны площадям живых сечений потока. Индекс “ср”, как уже указывалось, в практических приложениях обычно опускают.
Физический смысл уравнения неразрывности состоит в том, что он является проявлением закона сохранения массы для потока жидкости.
Дифференциальные уравнения неразрывности для трехмерного течения жидкости. Для трехмерного течения и неустановившегося движения справедливо:
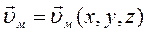 , ρ = ρ(х,y,z,t)
, ρ = ρ(х,y,z,t)
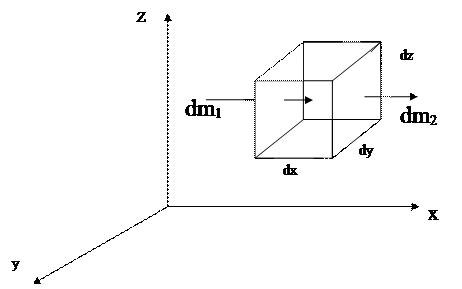
Рис. 1 1. Иллюстрация к выводу уравнения неразрывности
для трехмерного течения жидкости
Выделим внутри потока жидкости неподвижный элементарный параллелепипед (рис. 11) с ребрами dx, dy, dz. Согласно и аналогично полученному нами уравнению расхода для элементарной струйки, массовый расход жидкости, входящей в левую грань элементарного параллелепипеда (в направлении оси x) составит:
dM 1 = ρ υ м x · dS = ρ υ м x ∙ dydz
Тогда масса жидкости, вошедшей в левую грань за время dt:
dm 1 = dM 1 · dt = ρ υ м x ∙ dx dy dz dt
На противоположной (правой) грани параллелепипеда скорость жидкости и ее плотность могут измениться, поэтому массу жидкости, вышедшей из правой грани, следует записать:
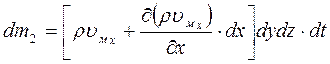
Отсюда изменение массы в объеме параллелепипеда в направлении оси x:
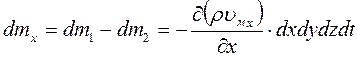
По аналогии изменение массы в направлениях осей y и z:
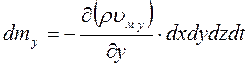
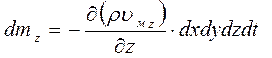
Полное изменение массы в объеме параллелепипеда:
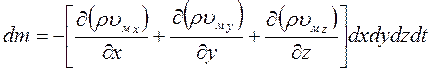
C другой стороны, исходя из определения плотности как предела отношения массы к объему, изменение массы dm в объеме параллелепипеда может быть представлено как конечное изменение плотности жидкости за время ее пребывания в фиксированном бесконечно малом объеме:
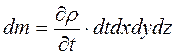
Приравняем два варианта выражения для dm:
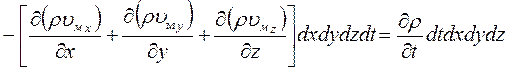
После сокращения получаем дифференциальное уравнение неразрывности для неустановившегося движения сжимаемой жидкости:
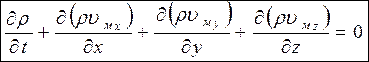
Для установившегося движения ∂ρ/∂ t = 0 (плотность не изменяется во времени). Для несжимаемой жидкости плотность не изменяется не только во времени, но и в пространстве (ρ = const), поэтому уравнение упрощается и переходит в дифференциальное уравнение неразрывности для установившегося движения несжимаемой (капельной) жидкости:
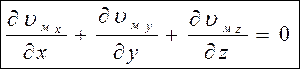
Дифференциальные уравнения движения
вязкой несжимаемой и идеальной жидкостей
Рассмотрим трехмерное неустановившееся ламинарное течение вязкой жидкости. В этом случае все гидравлические параметры потока и касательные напряжения сдвига являются функциями трех пространственных координат и времени.
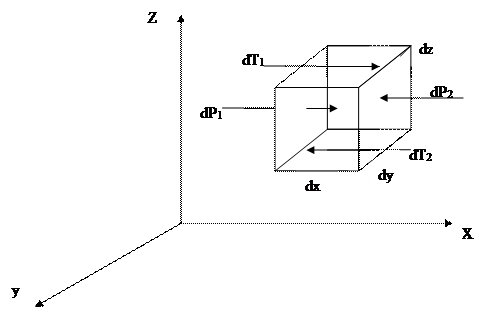
Рис. 12. Динамика движения жидкости в потоке
Выделим в массе движущейся жидкости неподвижный элементарный параллелепипед с длиной ребер dx, dy, dz (рис. 12). Масса жидкости в объеме параллелепипеда:
dm = ρ · dV = ρ ∙ dx dy dz
Используем основной принцип динамики: сумма сил, действующих на тело (в данном случае – на жидкость в объеме параллелепипеда) равна произведению его массы на ускорение, полученное в результате действия данных сил:
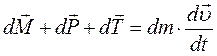
Рассмотрим данное уравнение в скалярной форме (в проекции на одну из осей координат – например, ось x):
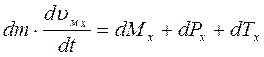
где dMx -проекция массовых сил на ось х;
dPx – проекция сил давления на ось х;
dTx – проекция сил вязкого трения на ось х.
При этом массовые силы пропорциональны массе жидкости и по закону Ньютона:
dMx = dm · X
где Х – проекция ускорения массовых сил на ось х. Соответственно:
dMy = dm · Y; dMz = dm · Z.
Силы давления действуют по всем граням параллелепипеда, однако эти силы (кроме dP1 и dP2) перпендикулярны оси х, поэтому их проекции на ось х равны 0 (мы их не изобразили на схеме, чтобы не перегружать чертеж). Но сила давления, действующая на левую грань, равна
dP 1 = p · dS = p · dy dz
При переходе жидкости из левой грани в правую (в направлении оси х) давление изменяется, что в дифференциальной форме может быть записано как p + (∂ p /∂ x) · dx, из чего следует:
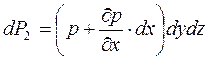
Это позволяет найти равнодействующую сил давления в направлении оси х:
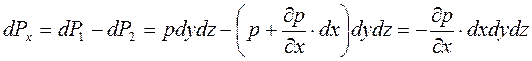
В общем случае при движении вязкой жидкости по всем граням параллелепипеда возникают касательные силы (силы вязкого трения).
В направлении оси х действуют только dT1 и dT2 (остальные силы дадут проекции, равные 0, поэтому на схеме не изображены):
dT 1 = τ · dx dy; 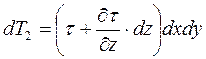
Записанные выражения справедливы лишь для одномерного течения (мы полагали, что υ м х изменяется только по координате z).
Для дальнейшего их обсуждения обратимся к закону вязкого трения:
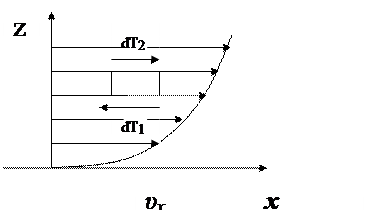

Рис. 1 3. Схема послойного течения жидкости
Исходя из модели послойного (ламинарного) течения жидкости (рис. 13) закон вязкого трения можно записать в виде:
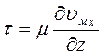
Для поля скоростей, изображенного на схеме, сила трения dT2 направлена слева направо, поскольку слой жидкости, движущейся над параллелепипедом, стремится сдвинуть параллелепипед в направлении скорости υx.
Сила трения dT1 направлена в обратную сторону, так как слой жидкости, движущейся под параллелепипедом, имеет меньшую скорость и подтормаживает жидкость на нижней грани параллелепипеда. При этом равнодействующая сил вязкого трения в направлении оси х равна:
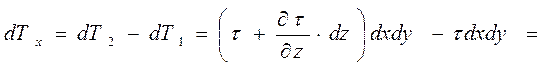
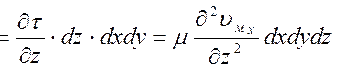
Имея в виду, что в общем случае течение может быть трехмерным, получаем:
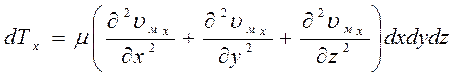
Подставляем значения проекций сил в основное уравнение:
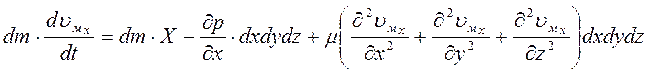
Поскольку dm = ρ ∙ dx dy dz, то в случае несжимаемой жидкости, когда ρ = const, получаем возможность делить на
ρ ∙ dx dy dz. Отсюда (c учетом того, что μ/ρ = ν):
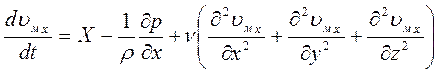
Здесь выражение в скобках – оператор Лапласа, поэтому более компактно дифференциальные уравнения движения вязкой несжимаемой жидкости в проекциях на все три координатные оси можно записать в виде:
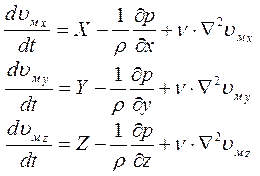
Полученная система уравнений (ее называют также уравнениями Навье - Стокса) не имеет общего решения, однако может быть использована:
1. Для решения наиболее простых гидродинамических задач;
2. Для постановки и решения более сложных задач численными методами с помощью современных компьютеров;
3. Для получения критериев гидродинамического подобия.
Дифференциальные уравнения движения идеальной жидкости (уравнения Эйлера). В идеальной жидкости вязкость отсутствует (ν = 0), поэтому последний член правой части уравнений Навье – Стокса становится равным 0. В результате уравнения упрощаются (переходят в систему уравнений движения Эйлера):
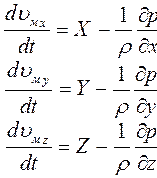
Интегрирование данной системы дифференциальных уравнений приводит к получению важнейшего уравнения гидродинамики – уравнения Бернулли.








 Пусть элементарная струйка имеет живое сечение dS и в данный момент времени занимает положение 1 (рис. 9). Через время dt сечение dS перемещается в направлении скорости υ и занимает новое положение 1' (все жидкие частицы в сечении dS имеют одинаковую скорость υ согласно струйной модели). За время dt сечение dS проходит путь, равный dl.
Пусть элементарная струйка имеет живое сечение dS и в данный момент времени занимает положение 1 (рис. 9). Через время dt сечение dS перемещается в направлении скорости υ и занимает новое положение 1' (все жидкие частицы в сечении dS имеют одинаковую скорость υ согласно струйной модели). За время dt сечение dS проходит путь, равный dl.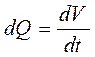 к выводу уравнения
к выводу уравнения 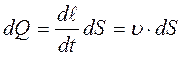
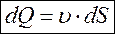
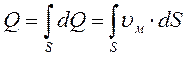
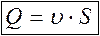
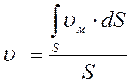 (см. раздел 1.23)
(см. раздел 1.23) 
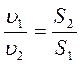 , т.е.
, т.е.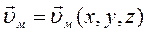 , ρ = ρ(х,y,z,t)
, ρ = ρ(х,y,z,t)