Альтернативное расписание новолуний в юлианском календаре для эпохи разрушения Иерусалимского храма

Иудейский календарь вплоть до IV в. н.э. основывался на реальных наблюдениях неомении — первого появления лунного серпа на вечернем небе. Обычно полагают, что специальная комиссия при иерусалимском синедрионе с помощью астрономических вычислений контролировала показания свидетелей, наблюдавших неомению. Вопрос же о переходе исключительно на вычисляемый лунно-солнечный календарь возник лишь после того, как в 70 г. н.э. Иерусалим был полностью разрушен войсками римского императора Веспасиана, а иудеи рассеялись по многим странам Европы и Азии. Вычисляемый иудейский календарь, официально действующий и сегодня, создавался в течение нескольких веков. В его основу положен тот же самый сирийский 19-летний цикл и то же самое вавилонское распределение эмболисмических годов в цикле, что получились при реконструкции цезаревского календаря. Поэтому правомерен вопрос: могли ли иудеи, например из Александрии, в тех случаях, когда запаздывало объявление синедриона о начале месяца, а вычисляемый календарь ещё не был официально введён, пользоваться цезаревским календарём, если, конечно, последний реально существовал?

В иудейском календаре, согласно Библии, религиозный год начинается с первого по счёту месяца авив — «месяца колосьев», в котором созревает ячмень. Но ячмень в окрестностях Иерусалима созревает весной, поэтому авив — месяц весенний. Позже этот месяц был переименован в месяц нисан, а началом гражданского года стал месяц тишри — седьмой месяц в религиозном году. Какие же месяцы в цезаревском календаре являются весенними? Поскольку лунно-солнечный год в этом календаре начинается в первое новолуние после зимнего солнцестояния, а промежуток времени между астрономическими моментами зимнего солнцестояния и весеннего равноденствия составляет чуть более трёх синодических месяцев, то под месяц нисан подходит либо третий, либо четвёртый лунный месяц.

Выбор конкретного месяца из указанных двух зависит от величины интервала между 25-м декабря и началом лунно-солнечного года. Очевидно, что при минимальных величинах этого интервала следует выбирать четвёртый месяц, а при максимальных — третий. Однако от величины этого же интервала зависит ещё и длина лунно-солнечного года: если интервал меньше 11 дней, то, согласно алгоритму «−11 или +19», год — эмболисмический. Этой корреляцией можно воспользоваться при промежуточных величинах рассматриваемого интервала, когда выбор нисана не очевиден и необходим дополнительный критерий. Действительно, самый простой способ выбора нисана в цезаревском календаре — это выбор четвёртого месяца в эмболисмических годах и третьего в простых (такие весенние месяцы в таблице 2 выделены курсивом). При этом как бы получается, что перенос нисана с третьего месяца на четвёртый обусловлен вставкой эмболисмического месяца именно перед этим нисаном, т.е. в конце религиозного года. Такой предложенный способ выбора нисана согласуется с исторически известным фактом, что эмболисмический месяц в древнем иудейском календаре вставлялся в конце религиозного года. Например, известно заявление председателя синедриона: «Поскольку голуби ещё малы и агнцы ещё очень молоды и к тому же время авива ещё не настало, то... мы признали за необходимое прибавить в этом году ещё тридцать дней» [1, с.246].

В вычисляемом иудейском календаре эмболисмический месяц веадар вставляется в конце религиозного года после 12-го месяца адар (перед нисаном). В эмболисмических годах адар имеет 30 дней, а веадар — 29; в простых же годах адар на один день короче, т.е. имеет 29 дней [2, с.120]. Если рассматривать не названия месяцев, а только их длину, то можно сказать, что 30-дневный эмболисмический месяц как бы вставляется не после 12-го месяца, а между 11-м и 12-м. Поскольку 11-й месяц — 30-дневный, то можно также сказать, что 30-дневный эмболисмический месяц как бы вставляется между 10-м и 11-м месяцами.

Таким образом, становится очевидной следующая переделка (модификация) цезаревского календаря в календарь «под иудейский»: 13-й месяц цезаревского календаря следует перенести в пределах эмболисмического года с последнего места на первое. При этом даты первых новолуний лунно-солнечных годов остаются прежними, а также сохраняется правило, что нечётные (уже по новой нумерации) месяцы — длинные, а чётные — короткие. Результат такой переделки показан в таблице 3. Если после этой (первой) переделки посмотреть на распределение длинных и коротких месяцев в году «от нисана до нисана» (нисан в таблице 3 выделен курсивом, а нумерация месяцев в году «от нисана до нисана» показана в последней строке), то получается следующая последовательность 30- и 29-дневных месяцев:

30 — 29 — 30 — 29 — 30 — 29 — 30 — 29 — 30 — 29 — (30) — 30 — 29,

в которой «месяц в скобках» вставляется только в эмболисмических годах. Но именно такая же последовательность применяется и в так называемых «нормальных» лунно-солнечных годах вычисляемого иудейского календаря [2, с.120].

Таблица 3 Альтернативное расписание новолуний в юлианском календаре (с 13-м месяцем в начале лунно-солнечного года). Обозначения: L — круг Луны сирийского цикла, точкой (•) обозначены эмболисмические годы; m — номер месяца в лунно-солнечном году (нечётный номер — 30-дневный месяц, чётный — 29-дневный), n — номер месяца при счёте от нисана, как в вычисляемом иудейском календаре (в первых трёх столбцах номера месяцев в эмболисмических годах указаны в скобках); курсивом обозначены новолуния весенних месяцев (нисана), жирным шрифтом — новолуния александрийского месяца тота, наклонным — новолуние нечётного, но 29-дневного месяца, т.е. месяца «скачка Луны»; звёздочкой (∗) обозначены новолуния месяца m=2, даты которых в високосные годы переносятся на один день назад.

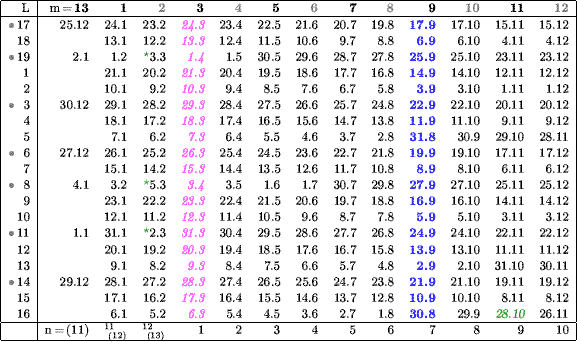
В этой «нормальной» последовательности (назовём её альтернативной по отношению к созигеновской) используется уже обсуждавшаяся во второй главе формальная длина лунных месяцев, так как в таблице 3 юлианские високосные дни — 29-е февраля — вставляются «в скрытом виде». Эти дни попадают в основном на месяц m=2, но иногда и на месяц m=1. При этом реальная длина месяца по сравнению с формальной увеличивается на один день. В тех случаях, когда 29-е февраля попадает на месяц m=1, этот месяц получается длиной в 31 день, что определённо не подходит для иудейского календаря. Поэтому необходимо сделать ещё одну (вторую) переделку, а именно — ввести исключение: начинать месяц m=2 в високосных годах с кругами Луны L = 8, 11 и 19 на один день раньше (соответствующие новолуния отмечены в таблице 3 звёздочкой). В итоге, после второй переделки дополнительный день в високосных годах всегда вставляется в 29-дневном месяце m=2 и месяцев длиной в 31 день не получается. Заметим, что такие вставки, а также «скачок Луны» в месяце m=11 при L=16 (удаление лишнего дня) можно назвать корректировкой средней длины календарного года.

Подобная корректировка проводится и в вычисляемом иудейском календаре. Так, для некоторых годов этого календаря либо девятый от нисана 30-дневный месяц укорачивается на один день, либо восьмой от нисана 29-дневный месяц удлинняется. Однако в вычисляемом иудейском календаре, в отличие от таблицы 3, выбор года, длина которого корректируется либо вставкой добавочного дня, либо удалением лишнего, определяется на основе алгоритма, оперирующего с многозначными цифрами.

Сравнивая вычисляемый иудейский календарь (описание которого можно найти, например, в книге И.А. Климишина [1, с.245]) с календарём, приведённым в таблице 3, можно заключить, что они совпадают между собой по следующим четырём признакам. В обоих календарях используются: а) сирийский 19-летний цикл, б) вавилонское распределение в цикле эмболисмических годов, в) альтернативное чередование в «нормальных» годах (т.е. в годах без корректировки их длины) длинных и коротких месяцев и г) выбор девятого от нисана месяца для корректирующего удаления его 30-го дня. Однако в этих двух календарях различаются: а) математические алгоритмы, определяющие выбор года для корректировки его длины, и б) номера месяцев (при счёте от нисана) для корректирующей вставки в них 30-го дня.

Перечисленных совпадений вполне достаточно, чтобы предположить, что переделанный (модифицированный) цезаревский календарь (таблица 3) мог служить основой для создания вычисляемого иудейского календаря. Всё, что в ту эпоху осталось сделать — это разработать более точный алгоритм выбора года для корректировки его длины и перенести вставку корректирующего дня с месяца m=2 на месяц m=10. Необходимость таких изменений была обусловлена, по-видимому, недостаточной точностью расписания новолуний в таблице 3, так как это расписание, согласно Гиппарху, ошибается на одни сутки за каждые 304 года и в его одновременно високосных и эмболисмических годах четыре 30-дневных месяца идут подряд.

Анализируя таблицу 3, можно указать на дополнительный аргумент в пользу применения в цезаревском календаре именно созигеновского, а не альтернативного распределения длинных и коротких месяцев: в этой таблице последний месяц лунно-солнечного года с кругом Луны L=8 начинается 25-го декабря, т.е. в первое новолуние после зимнего солнцестояния, а первый месяц следующего года — только во второе новолуние, что определённо противоречит первому принципу цезаревского календаря, но, по-видимому, не имеет значения для иудейского.

Теперь посмотрим, как приведённое в таблице 3 расписание новолуний согласуется с астрономическими фазами Луны в том 19-летии, в котором Иерусалим был разрушен войсками императора Веспасиана. Этим 19-летием, если его начинать как и в таблицах 1–3 с года L=17, является интервал с 57-го по 75-й гг. н.э. Расчёт по методике, которая уже использовалась (во второй главе) для цезаревского календаря, показывает, что средний момент астрономического новолуния в 57–75 гг. н.э. приходился на 17 час 54 мин по иерусалимскому времени того дня, который предшествовал календарному новолунию таблицы 3, т.е. примерно за 6 часов до полуночи в начале первых суток лунного месяца. Этот результат хорошо согласуется с тем фактом, что сутки у иудеев начинаются накануне вечером при заходе Солнца (Библия, кн. Левит, гл.23:32). Поэтому сделанное выше предположение можно уточнить следующим образом: модифицированный цезаревский календарь (таблица 3), который условно назовём «альтернативным лунно-солнечным календарём» (или кратко «альтернативным календарём»), после разрушения Иерусалимского храма, т.е. начиная с 70-х гг. н.э., вполне мог быть прообразом действующего вычисляемого иудейского календаря.

При обсуждении привязки календарных новолуний к астрономическим необходимо обратить внимание на следующую особенность. Для простоты изложения рассмотрим сначала пример привязки к «идеальным» новолуниям, который иллюстрируется на Рис.1. На этом рисунке интервалы времени между «идеальными» новолуниями (штрихи на линии 1), заменяющими в данном примере астрономические, равны точно 29,5 суткам, а календарные лунные месяцы длиной в 30 и 29 дней чередуются попеременно (штрихи на линии 2). Оптимальной привязкой в этом примере будет такое расположение на оси времени начальных моментов «идеальных» и календарных месяцев, при котором «идеальное» новолуние совпадает в среднем с началом календарного месяца, т.е. при котором (см. Рис.1) 29,5-дневный интервал симметрично расположен внутри 30-дневного, а 29-дневный — внутри 29,5-дневного. Особенностью такой оптимальной привязки является то, что в этом случае «идеальное» новолуние приходится или на четверть суток позже начала 30-дневного календарного месяца, или на четверть суток раньше начала 29-дневного (см. разметку 3 на Рис.1). Расчёт показывает, что отмеченная особенность с хорошей точностью выполняется в среднем и для реальных новолуний.

Рис. 1 Иллюстрация оптимальной привязки лунного календаря к фазам Луны. Обозначения: (1) — моменты времени «идеальных» новолуний с интервалом в 29,5 суток; (2) — начала календарных месяцев с попеременным чередованием длины в 30 и 29 дней; (3) — сдвижка (в сутках) момента времени «идеального» новолуния по отношению к началу календарного месяца.

Разделим все календарные лунные месяцы в таблице 3 на две группы: к первой группе отнесём 30-дневные месяцы, а ко второй — 29-дневные. В 57–75 гг. астрономические новолуния лунных месяцев как первой, так и второй группы приходились в среднем днём раньше соответствующих дат, приведённых в таблице 3. Однако в этих группах по отдельности средние моменты астрономических новолуний приходились на разное время: в первой группе — на 23 час 24 мин, а во второй — на 12 час 10 мин по иерусалимскому времени. Таким образом, особенностью уже реальной привязки лунно-солнечного календаря к фазам Луны является то, что по отношению к среднему моменту новолуния во всех месяцах цикла средний момент новолуния в 30-дневных месяцах цикла приходится примерно на 6 часов позже, а в 29-дневных — на 6 часов раньше. Можно также сказать: если средний момент новолуния во всех месяцах цикла приходится на закат, то средний момент новолуния в 30-дневных месяцах цикла — на полночь после этого заката, а в 29-дневных — на полдень до этого заката.

Месяц нисан в таблице 3 всегда имеет 30 дней, поэтому в 57–75 гг. средний за цикл момент астрономического новолуния в этом месяце приходился на полночь в начале первых суток, что хорошо согласуется с приведёнными в статье [7] пасхальными условиями привязки вычисляемого иудейского календаря к фазам Луны.

Заметим, что девятый месяц в таблице 3, выделенный жирным шрифтом, соответствует иудейскому месяцу тишри, в котором начинается гражданский новый год. Поэтому первое новолуние иудейского гражданского года, если его определять по таблице 3, и первое новолуние александрийского года соответствуют одному и тому же астрономическому новолунию.

Поэтому вполне возможно, что «предполагаемый прообраз вычисляемого иудейского календаря» связывался не только с юлианским календарём, но и с александрийским. Однако, «у историков, по-видимому, всё же имеется мало данных о том, что александрийский календарь получил широкое распространение. Так, писатель Цензорин в 238 г. подробно рассказывает о египетском календаре с его подвижным годом, но почему-то совершенно умалчивает об александрийском. Но уже столетием позже Феон Александрийский даёт исчерпывающие правила перехода от александрийских дат к египетским» [1, с.322].

Обратим внимание, что порядковый номер года в 19-летнем цикле (круг Луны) был определён пока только для лунно-солнечного года, начинающегося зимой — в первое новолуние после зимнего солнцестояния. А как перенести эту нумерацию на иудейские календарные годы, начинающиеся осенью (в гражданский новый год) и весной (в религиозный новый год)? Другими словами, как хронологически соотнести между собой годы, стоящие первыми в цикле, но относящиеся к разным стилям — к зимнему, осеннему и весеннему?

Будем исходить из того, что при любом стиле в цикле должно быть одно и то же распределение эмболисмических годов. Это условие будет выполняться, если годы, относящиеся к разным стилям, но содержащие внутри себя один и тот же эмболисмический месяц, будут иметь одно и то же значение для круга Луны. Учитывая сказанное, а также анализируя таблицу 3, где эмболисмический месяц помещён в начале «зимнего» года, можно сформулировать следующее правило: «осенний» год начинается раньше «зимнего», а «весенний» — раньше «осеннего». Например, согласно таблицам 1 и 3 начало первого после юлианской календарной реформы лунно-солнечного года с кругом Луны L=1 приходится на 21-е января 36 г. до н.э., но по осеннему и по весеннему стилям начало этого же года, т.е. с этим же кругом Луны L=1, приходится уже на 25-е сентября и на 1-е апреля 37 г. до н.э. соответственно.

Однако 1-го тишри 37 г. до н.э., если считать по осеннему стилю, начался не только иудейский (он же сирийский) 19-летний лунный цикл («малый круговорот»), но ещё и два других иудейских цикла — 7-летний цикл «субботнего года» и 28-летний солнечный цикл («большой круговорот»). У иудеев, согласно Библии, каждый седьмой год — это «суббота покоя земли» (кн. Левит, гл.25:4), т.е. так называемый «субботний год», в котором ограничиваются земледельческие работы. А 28-летний солнечный цикл — это период юлианского календаря, через который все его даты снова приходятся на те же дни недели. Действующий вычисляемый иудейский календарь практически не имеет периода повторяемости, поэтому можно предположить, что иудейский 28-летний цикл появился раньше него — в то время, когда создавался или уже был создан основанный на «расписании новолуний в юлианском календаре» прообраз вычисляемого иудейского календаря, и когда в иудейскую практику вводилась сдвижка даты нового года, если она выпадала на определённые дни недели — на воскресенье, среду и пятницу. Фактически это означало, что со сдвижками период повторяемости «расписания новолуний в юлианском календаре» увеличивался с 19-ти до 19×28 = 532-х лет. По определению все три цикла (лунный, солнечный и семилетний) начались 1-го тишри 1-го года иудейской эры от «сотворения мира», т.е. 7-го октября по ст.ст. 3761 г. до н.э. Именно поэтому число лет между 3761-м и 37-м гг. до н.э. в точности равно произведению длин этих трёх циклов: 3761−37 = 19×28×7. Любопытно, что в июле этого 37-го г. до н.э., в котором впервые после «сотворения мира» все три цикла снова сошлись вместе, библейский царь Ирод захватил Иерусалим и стал фактическим правителем Иудеи [3, с.281]. Заметим, что годы правления ветхозаветных царей отсчитывались от нисана (авива), т.е. по весеннему стилю.

В исторической литературе можно встретить четыре разных стиля летосчисления, определяемые выбором начала года — это так называемые январский, сентябрьский, мартовский и ультрамартовский годы [1, с.380]. Известно, что сентябрьский год начинается на четыре месяца раньше январского (с тем же обозначением), мартовский год — на шесть месяцев позже сентябрьского и ультрамартовский год — на шесть месяцев раньше сентябрьского. Сравнивая эти исторически известные стили с теми, которые были выше введены для таблицы 3, можно связать январский год с «зимним», сентябрьский — с «осенним», а ультрамартовский — с «весенним». Однако с чем же тогда связать исторически известный мартовский год?

Сохранив требование, чтобы годы, относящиеся к разным стилям, но содержащие внутри себя один и тот же эмболисмический месяц, имели бы одно и то же значение для круга Луны, проанализирум теперь таблицу 2, где, в отличие от таблицы 3, эмболисмический месяц помещён в конце «зимнего» года. В этом случае получается совсем другое правило: «весенний» год начинается позже «зимнего». Таким образом, если эмболисмическим месяцем «зимнего» года, считается месяц в конце этого года, то получается мартовский стиль, а если — в начале, то — ультрамартовский.