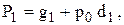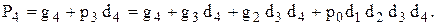Многоразрядная схема сравнения служит для регистрации совпадения двух n-разрядных чисел:
 и
и  .
.
Она строится из n одноразрядных схем, сравнивающих цифры  и
и 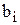 этих чисел поразрядно.
этих чисел поразрядно.
На основе таблицы истинности одноразрядной системы сравнения (табл.1) определить СДНФ функции равнозначности  и функции неравнозначности
и функции неравнозначности 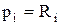
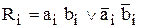 (ИЛИ) (+) (3.1)
(ИЛИ) (+) (3.1)
 . (3.2)
. (3.2)
Для обнаружения совпадений  и
и  во всех разрядах чисел А и В следует образовать конъюнкции всех n переменных, т.е.
во всех разрядах чисел А и В следует образовать конъюнкции всех n переменных, т.е.

или
 .
.
Многоразрядная схема сравнения двух чисел А и В представляет собой логическую схему, реализующую ПФ вида (3) или (4). На рис. 1 приведена схема сравнения на ЛЭ типа И и ИЛИ для  по функции равнозначности и изображено условное обозначение схемы сравнения.
по функции равнозначности и изображено условное обозначение схемы сравнения.
Более универсальными являются цифровые компараторы, которые, помимо регистрации равенства двух чисел, могут установить, какое из них больше. Обычно такие компараторы имеют три выхода  ,
,  и
и 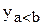 . Простейшая задача состоит в сравнении двух одноразрядных чисел
. Простейшая задача состоит в сравнении двух одноразрядных чисел  и
и 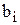 . Такое сравнение реализуется следующими ПФ:
. Такое сравнение реализуется следующими ПФ:
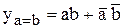


Аналогичные ПФ могут быть составлены для сравнения многоразрядных чисел. Однако при увеличении разрядности сложность этих ПФ быстро растёт и форма их представления теряет надёжность. Поэтому для сравнения многоразрядных чисел используют следующий алгоритм. Сначала сравнивают значения старших разрядов; если они различны, то эти разряды и определяют результаты сравнения; если же они равны, то необходимо сравнивать следующие за ними более младшие разряды и т.д. При этом многоразрядный компаратор может быть реализован в виде каскадного соединения более простых первичных компараторов, имеющих дополнительно входы  ,
,  ,
,  , соединяемые с одноимёнными выходами первичного компаратора предыдущего каскада (рис. 3.9.).
, соединяемые с одноимёнными выходами первичного компаратора предыдущего каскада (рис. 3.9.).
Рис. 3.9.
Одноразрядный первичный компаратор описывается следующими ПФ:

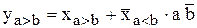

Первичные компараторы на четыре и более разрядов выпускаются в интегральном исполнении.
Одноразрядный полусумматор
При сложении младших разрядов  и
и  двух чисел А и В цифра переноса
двух чисел А и В цифра переноса 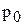 в этот разряд всегда равна нулю. Поэтому сумматор, используемый в этом разряде, может иметь всего два входа.
в этот разряд всегда равна нулю. Поэтому сумматор, используемый в этом разряде, может иметь всего два входа.
Сумматор такого типа называется полусумматором, он обозначается, как показано на рис. 3.10, а функционирует в соответствии с таблицей истинности, представленной в табл. 3.2. Из неё легко получить ПФ в СДНФ:
Рис. 3.10.


Таблица 3.2.
Одноразрядный сумматор
Сумматором называется логическое устройство, выполняющее операцию арифметического сложения двух чисел.
Наиболее широко используются комбинационные сумматоры, которые выполняются в виде комбинационных схем (без элементов памяти).
Сложение двух чисел  и
и  обычно выполняется поразрядно одноразрядным сумматором. При этом сумматор складывает цифры
обычно выполняется поразрядно одноразрядным сумматором. При этом сумматор складывает цифры  и
и 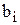 i-го разряда слагаемых, а также цифру переноса
i-го разряда слагаемых, а также цифру переноса  из младшего (i-1)-го разряда. В результате получится цифра
из младшего (i-1)-го разряда. В результате получится цифра 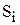 i-го разряда суммы и цифра переноса
i-го разряда суммы и цифра переноса  в следующий (i +1) – й разряд.
в следующий (i +1) – й разряд.
Отсюда ясно, что одноразрядный сумматор имеет три входа

и два выхода

и обозначается, как показано на рис. 3.11.
Рис. 3.11.
Закон функционирования одноразрядного сумматора описывается таблицей истинности, которая отражает правила сложения трёх двоичных чисел (табл.1). На основе табл. 3.1. составим ПФ суммы 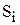 и переноса
и переноса  в СДНФ.
в СДНФ.
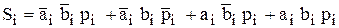 (3.3)
(3.3)
 (3.4)
(3.4)
Выражения (2) минимизируется путём добавления двух слагаемых вида  и попарного склеивания соседних слагаемых
и попарного склеивания соседних слагаемых
 (3.5)
(3.5)
На рис. 3.12 приведена схема сумматора, реализованная на ЛЭ типа И, ИЛИ по выражениям (3.3), (3.5).
Рис. 3.12.
Для обработки многоразрядных чисел объединяется соответствующее число одноразрядных сумматоров. При этом отдельные разряды обрабатываемых чисел А и В подаются на входы  и
и 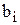 . На вход
. На вход  подаётся перенос из предыдущего, более младшего разряда. Формируемый в данном разряде перенос
подаётся перенос из предыдущего, более младшего разряда. Формируемый в данном разряде перенос  передаётся в следующий, более старший разряд (рис. 3.13.).
передаётся в следующий, более старший разряд (рис. 3.13.).

Рис. 3.13 Рис. 3.14
Время выполнения операции в сумматоре, построенном таким образом, существенно больше времени сложения в одноразрядном сумматоре. Действительно, сигнал переноса  только тогда может принять правильное значение, когда перед этим будет установлено правильное значение
только тогда может принять правильное значение, когда перед этим будет установлено правильное значение  .
.
Такой порядок выполнения операции называется последовательным переносом. Чтобы уменьшить время, необходимое для сложения многоразрядных чисел, можно использовать схему переноса, в которой все сигналы переноса вычисляются параллельно непосредственно по значениям входных переменных. Полагая, что входная переменная с полного одноразрядного сумматора, работающего в i-м разряде многоразрядного сумматора, используется в качестве сигнала переноса из предыдущего разряда, т.е.  в соответствии с (3.5) выражение для сигнала переноса
в соответствии с (3.5) выражение для сигнала переноса  , формируемого в этом разряде, представим в виде:
, формируемого в этом разряде, представим в виде:
 (3.6)
(3.6)
где  – функции входных переменных
– функции входных переменных  , называемые функцией генерации переноса
, называемые функцией генерации переноса 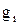 и функцией распространения переноса
и функцией распространения переноса  .
.
Важно, что значения 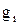 и
и  не зависят от
не зависят от  , т.е. могут быть вычислены с минимальной задержкой. Функция распространения переноса
, т.е. могут быть вычислены с минимальной задержкой. Функция распространения переноса  при
при  может принимать произвольное значение, поскольку значение
может принимать произвольное значение, поскольку значение  обеспечивается первым членом выражения (3.6) независимо от значения
обеспечивается первым членом выражения (3.6) независимо от значения  .
.
Пользуясь выражением (3.6), можно вывести следующие формулы для вычисления сигналов переноса:
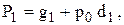


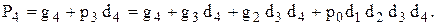

Устройство, реализующее указанные функции в параллельной форме, называют схемой ускоренного переноса. На функциональных схемах его обычно обозначают символом GRP.
Схема четырёхразрядной секции сумматора с параллельным переносом и её условное обозначение показаны соответственно на рис. 3.15 а и рис. 3.15 б.
а) б)
Рис. 3.15.
Обратите внимание на изменение обозначения одноразрядных секций, вызванное тем, что в данном случае входы одноразрядного сумматора по отношению к выходам G и D не равноценны. Усложнение схемы такой секции окупается существенным повышением быстродействия, поскольку в ней значения выходных сигналов старших и младших разрядов формируются одновременно.
Лекция №4





 и
и  .
. и
и 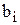 этих чисел поразрядно.
этих чисел поразрядно. и функции неравнозначности
и функции неравнозначности 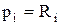
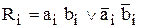 (ИЛИ) (+) (3.1)
(ИЛИ) (+) (3.1) . (3.2)
. (3.2) во всех разрядах чисел А и В следует образовать конъюнкции всех n переменных, т.е.
во всех разрядах чисел А и В следует образовать конъюнкции всех n переменных, т.е.
 .
. по функции равнозначности и изображено условное обозначение схемы сравнения.
по функции равнозначности и изображено условное обозначение схемы сравнения.




 ,
,  и
и 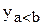 . Простейшая задача состоит в сравнении двух одноразрядных чисел
. Простейшая задача состоит в сравнении двух одноразрядных чисел  и
и 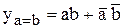


 ,
,  ,
,  , соединяемые с одноимёнными выходами первичного компаратора предыдущего каскада (рис. 3.9.).
, соединяемые с одноимёнными выходами первичного компаратора предыдущего каскада (рис. 3.9.).


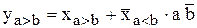

 и
и  двух чисел А и В цифра переноса
двух чисел А и В цифра переноса 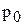 в этот разряд всегда равна нулю. Поэтому сумматор, используемый в этом разряде, может иметь всего два входа.
в этот разряд всегда равна нулю. Поэтому сумматор, используемый в этом разряде, может иметь всего два входа.





 и
и  обычно выполняется поразрядно одноразрядным сумматором. При этом сумматор складывает цифры
обычно выполняется поразрядно одноразрядным сумматором. При этом сумматор складывает цифры  из младшего (i-1)-го разряда. В результате получится цифра
из младшего (i-1)-го разряда. В результате получится цифра 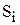 i-го разряда суммы и цифра переноса
i-го разряда суммы и цифра переноса  в следующий (i +1) – й разряд.
в следующий (i +1) – й разряд.
 и два выхода
и два выхода  и обозначается, как показано на рис. 3.11.
и обозначается, как показано на рис. 3.11.
 в СДНФ.
в СДНФ.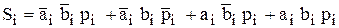 (3.3)
(3.3) (3.4)
(3.4) и попарного склеивания соседних слагаемых
и попарного склеивания соседних слагаемых (3.5)
(3.5)


 в соответствии с (3.5) выражение для сигнала переноса
в соответствии с (3.5) выражение для сигнала переноса  (3.6)
(3.6) – функции входных переменных
– функции входных переменных  , называемые функцией генерации переноса
, называемые функцией генерации переноса 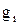 и функцией распространения переноса
и функцией распространения переноса  .
. , т.е. могут быть вычислены с минимальной задержкой. Функция распространения переноса
, т.е. могут быть вычислены с минимальной задержкой. Функция распространения переноса  при
при  может принимать произвольное значение, поскольку значение
может принимать произвольное значение, поскольку значение  обеспечивается первым членом выражения (3.6) независимо от значения
обеспечивается первым членом выражения (3.6) независимо от значения