Текст основной программы приведён ниже.
Программа 1.
#include "stdafx.h"
#include <iostream>
#include <math.h> //необходимые заголовочные файлы
#include <conio.h>
#include <fstream>
using namespace std;
double U(double t,double x,double u)
{
return u;
}
double fi(double x)
{
return pow(x,2)/2; //функция 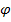 , первое приближение
, первое приближение
}
int _tmain(int argc, _TCHAR* argv[])
{
double T0=5; //определяем физические ограничения по t
const int nt=25;//число значений t
double T[nt]; //массив значений t
double S[nt]; //массив значений s
double dt=T0/(nt-1);//шаг по переменной t
T[0]=0;//начальное значение t, первый элемент массива
S[0]=0;
for (int i=1;i<nt;i++)
{
T[i]=T[i-1]+dt;//заполнение массива значений по t
S[i]=S[i-1]+dt;
}
double X0=20;//определяем ограничения по x
const int nx=20;//число значнеий x
double X[nx];//массив значений x
double dx;
dx=X0/(nx-1);//шаг по переменной x
X[0]=-X0/2;//первый элемент массива
for (int i=1;i<nx;i++)//заполнение массива значений по x
{
X[i]=X[i-1]+dx;
}
/*Массивы значений функций 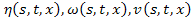 (V1 и V – два соседних приближения)*/
(V1 и V – два соседних приближения)*/
double u[nt][nx];
double (*eta)[nt][nx];
eta=new double[nt][nt][nx];
double (*eta1)[nt][nx];
eta1=new double[nt][nt][nx];
double (*V)[nt][nx];
V=new double[nt][nt][nx];
double (*W)[nt][nx];
W=new double[nt][nt][nx];
double (*V1)[nt][nx];
V1=new double[nt][nt][nx];
for (int i=0;i<nx;i++) /*заполнение массивов при 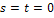 (начальное условие
(начальное условие  )*/
)*/
{
u[0][i]=fi(X[i]);
eta[0][0][i]=X[i];
V[0][0][i]=u[0][i];
}
for (int i=0;i<nt;i++)
{
for (int j=0;j<nt;j++)
{
for (int k=0;k<nx;k++)
{
V[i][j][k]=fi(X[k]); //заполнение массива 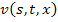
}
}
}
for (int j=0;j<nt;j++)
{
for (int k=0;k<nx;k++)
{
u[j][k]=fi(X[k]); //определение функции 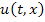
}
}
ofstream out("fi.txt");
out<<nx<<endl;
for (int i=0;i<nx;i++)
{
for (int j=0;j<nt;j++)//t
{
out<<u[j][i]<<"\t"; //запись значений функции 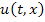 в файл
в файл
}
out<<endl;
}
out.close();
/* определение переменных, с помощью которых обеспечивается выход из программы и сходимость последовательных приближений */
double sumst=0,sumst1=0,sumst2=0,sum0s=0,sum0s1=0,sum0s2=0;
double e=0.0001;
double dif=11;
double dif1=0;
double difeta=15;
double difeta1=0;
double dif2=0;
for (int n=0;n<5;n++)
{
for (int n=0;n<5;n++)
{
dif=0;//max raznost
difeta=0;//max raznost
//заполнение массива eta
for (int k=0;k<nx;k++)//x
{
for (int j=0;j<nt;j++)//t
{
for (int i=0;i<nt;i++)//s
{
if (i<=j)
{
sumst=0;
//вычисление интеграла 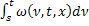
for (int s1=i;s1<j;s1++)
{
sumst+=V[s1][j][k]*dt;
}
eta1[i][j][k]=X[k]-sumst;
}
if (i>j)
{
sumst=0;
for (int s1=i;s1>j;s1--)
{
sumst+=V[s1][j][k]*dt;
}
eta1[i][j][k]=X[k]+sumst;
}
difeta1=fabs(eta1[i][j][k]-eta[i][j][k]);
if (difeta1>difeta) difeta=difeta1;
}
}
}
cout<<"difeta = "<<difeta<<endl;
//заполнение массива V [i][j][k] и W[i][j][k]
for (int k=0;k<nx;k++)//x
{
for (int j=0;j<nt;j++)//t
{
for (int i=0;i<nt;i++)//s
{
V1[i][j][k]=eta1[0][j][k]*exp(-2.0*i);
sum0s=0;
for (int s2=0;s2<i;s2++)
{
sum0s+=exp(2.0*s2)*V1[s2][j][k]*V1[s2][j][k]*dt;
}
W[i][j][k]=exp(-2.0*i)*(eta1[0][j][k]*eta1[0][j][k]*0.5+sum0s);
dif1=fabs(V1[i][j][k]-V[i][j][k]);
if (dif1>dif) dif=dif1;
}
}
}
cout<<dif<<endl;
if (fabs(dif2-dif)<e) break;
dif2=dif;
for (int k=0;k<nx;k++)//x
{
for (int j=0;j<nt;j++)//t
{
for (int i=0;i<nt;i++)//s
{
V[i][j][k]=V1[i][j][k]; /*последнее приближение становится предыдущим и цикл продолжается */
eta[i][j][k]=eta1[i][j][k]; //аналогично
}
}
}
}
for (int k=0;k<nx;k++)//x
{
for (int j=0;j<nt;j++)//t
{
u[j][k]=W[j][j][k]; /*присваиваем функции u значения массива W[j][j][k] */
}
}
}
ofstream out2("u.txt");
out2<<nx<<endl;
for (int i=0;i<nx;i++)
{
for (int j=0;j<nt;j++)//t
{
out2<<u[j][i]<<"\t"; //запись результатов в файл
}
out2<<endl;
}
out2.close();
/* запись файла значений известной функции u */
for (int k=0;k<nx;k++)//x
{
for (int j=0;j<nt;j++)//t
{
u[j][k]=(X[k]*X[k])/(4*exp(2.0*T[j])-2); }
}
ofstream out3("fu.txt");
out3<<nx<<endl;
for (int i=0;i<nx;i++)
{
for (int j=0;j<nt;j++)//t
{
out3<<u[j][i]<<"\t";
}
out3<<endl;
}
out3.close();
delete []eta;
delete []eta1;
delete []V;
delete []V1;
getch();
return 0;
}
Результаты вычислений записываются в три файла. Первый файл 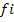 содержит значения функции
содержит значения функции  . Графически её можно представить так:
. Графически её можно представить так:
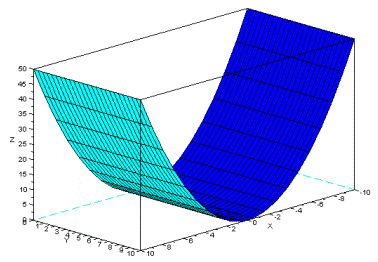
Во второй файл записываются результаты вычислений в самой программе. Функция 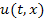 выглядит так:
выглядит так:
В третий файл записываются значения функции  , зная что
, зная что
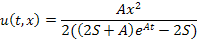
Тогда графически это будет иметь вид:
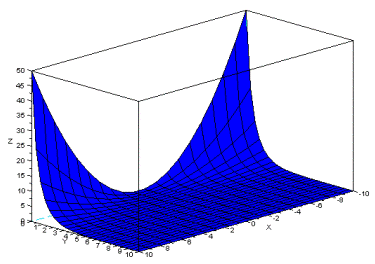
Таким образом, графики функций, построенные по результатам вычислений в программе и непосредественно, почти совпадают.
Пример 2. Рассмотрим более сложное уравнение. В качестве функции  выберем
выберем

Тогда исходное уравнение примет вид:

В качестве начального условия возьмём функцию

Тогда

Уравнения системы (26) перепишутся в виде:
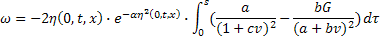
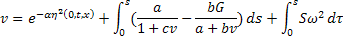
Аналогично составляем программу численного решения. Заметим, что в этом случае не получится непосредственно вычислить 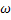 . Придётся находить значения обеих функций
. Придётся находить значения обеих функций 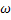 и
и 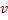 по их предыдущим приближениям.
по их предыдущим приближениям.
Возьмём следующие значения параметров: 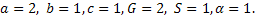 Тогда функция f примет вид:
Тогда функция f примет вид:

При увеличении значений 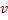 значения функции
значения функции  стремятся к нулю.
стремятся к нулю.
Таким образом, в программе используются следующие уравнения:
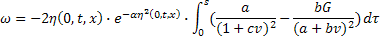
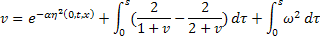
Программа 2.
#include "stdafx.h"
#include <iostream>
#include <math.h>
#include <conio.h>
#include <fstream>
using namespace std;
double U(double t,double x,double u)
{
return u;
}
double fi(double x)
{
return exp(-pow(x,2));
}
double fi1(double x)
{
return -2*x*exp(-pow(x,2));
}
int _tmain(int argc, _TCHAR* argv[])
{
double T0=5;
const int nt=25;
double T[nt];
double S[nt];
double dt=T0/(nt-1);
T[0]=0;
S[0]=0;
for (int i=1;i<nt;i++)
{
T[i]=T[i-1]+dt;
S[i]=S[i-1]+dt;
}//return 2.0;
double X0=20;
const int nx=20;
double X[nx];
double dx;
dx=X0/(nx-1);
//cout<<dx<<endl;
X[0]=-X0/2;
for (int i=1;i<nx;i++)
{
X[i]=X[i-1]+dx;
}
double u[nt][nx];
double (*eta)[nt][nx];
eta=new double[nt][nt][nx];
double (*eta1)[nt][nx];
eta1=new double[nt][nt][nx];
double (*V)[nt][nx];
V=new double[nt][nt][nx];
double (*W)[nt][nx];
W=new double[nt][nt][nx];
double (*V1)[nt][nx];
V1=new double[nt][nt][nx];
double (*W1)[nt][nx];
W1=new double[nt][nt][nx];
for (int i=0;i<nx;i++)
{
u[0][i]=fi(X[i]);
eta[0][0][i]=X[i];
V[0][0][i]=u[0][i];
}
//V0(s,t,x)=fi(x)
for (int i=0;i<nt;i++)
{
for (int j=0;j<nt;j++)
{
for (int k=0;k<nx;k++)
{
V[i][j][k]=fi(X[k]);
//cout<<V[i][j][k]<<endl;
}
}
}
for (int j=0;j<nt;j++)
{
for (int k=0;k<nx;k++)
{
u[j][k]=fi(X[k]);
}
}
for (int i=0;i<nt;i++)
{
for (int j=0;j<nt;j++)
{
for (int k=0;k<nx;k++)
{
W[i][j][k]=fi1(X[k]);
//cout<<V[i][j][k]<<endl;
}
}
}
ofstream out("fi.txt");
out<<nx<<endl;
for (int i=0;i<nx;i++)
{
for (int j=0;j<nt;j++)//t
{
out<<u[j][i]<<"\t";
}
out<<endl;
}
out.close();
double sumst=0,sumst1=0,sumst2=0,sum0s=0,sum0s1=0,sum0s2=0;
double e=0.0001;
double dif=11;
double dif1=0;
double difeta=15;
double difeta1=0;
double dif2=0;
for (int n=0;n<5;n++)
{
for (int n=0;n<5;n++)
{
dif=0;//max raznost
difeta=0;//max raznost
for (int k=0;k<nx;k++)//x
{
for (int j=0;j<nt;j++)//t
{
for (int i=0;i<nt;i++)//s
{
if (i<=j)
{
sumst=0;
for (int s1=i;s1<j;s1++)
{
sumst+=V[s1][j][k]*dt;
}
eta1[i][j][k]=X[k]-sumst;//sumst=integral ot s(i) do t(j) ot Vn-1=sum(V*dt)
}
if (i>j)
{
sumst=0;
for (int s1=i;s1>j;s1--)
{
sumst+=V[s1][j][k]*dt;
}
eta1[i][j][k]=X[k]+sumst;//sumst=integral ot s(i) do t(j) ot Vn-1=sum(V*dt)
}
difeta1=fabs(eta1[i][j][k]-eta[i][j][k]);
if (difeta1>difeta) difeta=difeta1; //нахождение максимальной разности между приближениями eta
}
}
}
cout<<"difeta = "<<difeta<<endl;
for (int k=0;k<nx;k++)//x
{
for (int j=0;j<nt;j++)//t
{
for (int i=0;i<nt;i++)//s
{
for (int s2=0;s2<i;s2++)
{
sumst1+=(2/((1+V[s2][j][k])*(1+V[s2][j][k]))-2/((1+V[s2][j][k])*(1+V[s2][j][k])))*dt;
}
W1[i][j][k]=exp(-eta1[0][j][k]*eta1[0][j][k])*(-2*(eta1[0][j][k]))*sumst1;
sum0s=0;
for (int s2=0;s2<i;s2++)
{
sum0s+=(2/(1+V[s2][j][k])-2/(1+V[s2][j][k]))*dt;
}
sumst2=0;
for (int s2=0;s2<i;s2++)
{
sumst2+=(W[s2][j][k]*W[s2][j][k])*dt;
}
V1[i][j][k]=exp(-eta1[0][j][k]*eta1[0][j][k])+sum0s+sumst2;
//V1[i][j][k]=fi(X[k])*exp(-sum0s);
dif1=fabs(V1[i][j][k]-V[i][j][k]);
cout<<"ijk"<<"\t"<<i<<"\t"<<j<<"\t"<<k<<"\t"<<V1[i][j][k]<<"\t"<<V[i][j][k]<<"\tdif"<<dif<<endl;
if (dif1>dif) dif=dif1; //нахождение максимальной разности между соседними приближениями
}
}
}
cout<<dif<<endl;
if (fabs(dif2-dif)<e) break; //Условие завершения программы
dif2=dif;
for (int k=0;k<nx;k++)//x
{
for (int j=0;j<nt;j++)//t
{
for (int i=0;i<nt;i++)//s
{
V[i][j][k]=V1[i][j][k];
W[i][j][k]=W1[i][j][k];
eta[i][j][k]=eta1[i][j][k];
}
}
}
}
for (int k=0;k<nx;k++)//x
{
for (int j=0;j<nt;j++)//t
{
u[j][k]=V[j][j][k];
}
}
}
ofstream out2("u.txt");
out2<<nx<<endl;
for (int i=0;i<nx;i++)
{
for (int j=0;j<nt;j++)//t
{
out2<<u[j][i]<<"\t";
}
out2<<endl;
}
out2.close();
delete []eta;
delete []eta1;
delete []W;
delete []W1;
delete []V;
delete []V1;
getch();
return 0;
}
Результаты вычислений записываются в два файла. Первый файл 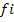 содержит значения функции
содержит значения функции  . Графически (спомощью пакета для математических расчётов Scilab 5.2.2) её можно представить так:
. Графически (спомощью пакета для математических расчётов Scilab 5.2.2) её можно представить так:
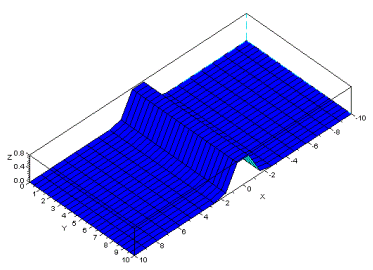
Во второй файл записываются результаты вычислений в самой программе. Функция 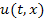 выглядит так:
выглядит так:
Заключение.
Таким образом, метод дополнительного аргумента может быть эффективно использован для приближённого решения нелинейных дифференциальных уравнений в частных производных.
В работе исходное дифференциальное уравнение преобразовано в систему из двух квазилинейных уравнений. А посредством метода дополнительного аргумента эта система сведена к системе интегральных уравнений, достаточно простых по структуре. Затем эта система решается с помощью численных методов с последующей реализацией на ПК. Получены трёхмерные графики функции 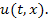
Доказательство существования решения задачи Коши (1) – (2) позволяет применять метод аргумента для решения уравнения (1) с различными функциями  , что иллюстрируется примерами.
, что иллюстрируется примерами.
Литература
1. Алексеенко, С. Н., Эгембердиев Ш. А. Применение метода дополнительного аргумента к одномерному аналогу задачи протекания // Материалы IV научной конференции КРСУ, Бишкек, май 1997г. – Бишкек: КРСУ, 1997.-С.26.
2. Алексеенко, С. Н., Эгембердиев Ш. А. Применение метода дополнительного аргумента к системе нелинейных уравнений типа полной производной по времени // Исслед. по интегродифференциальным уравнениям. – Бишкек: Илим, 1997. – Вып.26. - С. 161-169.
3. Алексеенко, С. Н., Эгембердиев Ш. А. Применение метода дополнительного аргумента к одномерному варианту задачи протекания с краевыми условиями третьего типа для скорости // Исслед. по интегродифференциальным уравнениям. – Бишкек: Илим, 1998. – Вып.27. - С. 225-243.
4. Алексеенко, С. Н., Эгембердиев Ш. А. Решение системы уравнений в частных производных первого порядка с начально-краевыми условиями методом дополнительного аргумента // Традиции и новации в культуре университетского образования (КТУ): Сб. трудов международ. науч. конференц. – Бишкек: Технология, 1998. – С.106-112.
5. Смирнов В. И. Курс высшей математики. Т. IV, Физматгиз. 1958.
6. Петровский И.Г. Лекции по теории обыкновенных дифференциальных уравнений. Изд. «Наука». М. 1970. 280 с.
Оглавление
Введение. 1
Постановка начальной задачи. 2
Применение метода дополнительного аргумента к решению характеристической системы. 3
Доказательство эквивалентности систем (8) и (26). 6
Доказательство существования решения задачи Коши 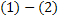 .............. 12
.............. 12
Постановка задачи численного расчёта. 30
Дискретизация исходной задачи и её решение итерациями. 34
Программа и её описание. Результаты вычислений. 36
Заключение. 51
Литература. 52





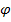 , первое приближение
, первое приближение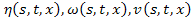 (V1 и V – два соседних приближения)*/
(V1 и V – два соседних приближения)*/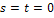 (начальное условие
(начальное условие  )*/
)*/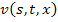
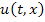
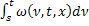
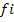 содержит значения функции
содержит значения функции  . Графически её можно представить так:
. Графически её можно представить так:
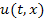 выглядит так:
выглядит так:
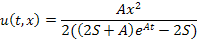

 выберем
выберем



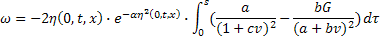
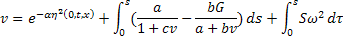
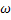 . Придётся находить значения обеих функций
. Придётся находить значения обеих функций 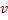 по их предыдущим приближениям.
по их предыдущим приближениям.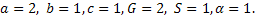 Тогда функция f примет вид:
Тогда функция f примет вид:
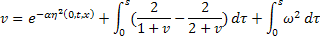


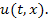
 , что иллюстрируется примерами.
, что иллюстрируется примерами.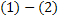 .............. 12
.............. 12

