Приближенное вычисление значений функции
Пусть требуется вычислить значение функции f(x) при  с заданной точностью
с заданной точностью 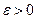
Если функцию f(x) в интервале (-R;R) можно разложить в степенной ряд 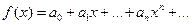
и  , то точное значение
, то точное значение  равно сумме этого ряда при
равно сумме этого ряда при  , т.е.
, т.е. 
а приближенное – частичной сумме  , т.е.
, т.е.
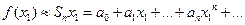
Точность этого равенства увеличивается с ростом n. Абсолютная погрешность этого приближенного равенства равна модулю остатка ряда, т.е.  ,
,
где

Таким образом, ошибку  можно найти, оценив остаток
можно найти, оценив остаток 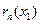 ряда.
ряда.
Для рядов лейбницевского типа

В остальных случаях (ряд знакопеременный или знакоположительный) составляют ряд из модулей членов ряда и для него стараются найти положительный ряд с большими членами, который легко бы суммировался. И в качестве оценки 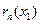 берут величину остатка этого нового ряда.
берут величину остатка этого нового ряда.
Приближенное вычисление определенных интегралов
Бесконечные ряды применяются также для приближенного вычисления неопределенных и определенных интегралов в случаях, когда первообразная не выражается в конечном итоге через элементарные функции либо нахождение первообразной сложно.
Пусть требуется вычислить  с точностью до
с точностью до 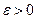 . Если подынтегральную функцию f(x) можно разложить в ряд по степеням x и интервал сходимости (-R;R) включит в себя отрезок [a;b], то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда. Ошибку вычислений определяют так же, как и при вычислении значений функций.
. Если подынтегральную функцию f(x) можно разложить в ряд по степеням x и интервал сходимости (-R;R) включит в себя отрезок [a;b], то для вычисления заданного интеграла можно воспользоваться свойством почленного интегрирования этого ряда. Ошибку вычислений определяют так же, как и при вычислении значений функций.
Приближенное решение дифференциальных уравнений
Если решение дифференциального уравнения не выражается через элементарные функции в конечном виде или способ его решения слишком сложен, то для приближенного решения уравнения можно воспользоваться рядом Тейлора.
Числовые ряды
Основные понятия
Числовым рядом называется выражение вида

где  – действительные или комплексные числа, называемые членами ряда,
– действительные или комплексные числа, называемые членами ряда, 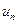 - общим членом ряда.
- общим членом ряда.
Ряд считается заданным, если известен общий член ряда 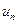 , выраженный как функция его номера n:
, выраженный как функция его номера n: 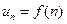 .
.
Сумма первых n членов ряда называется n -й частичной суммой ряда и обозначается через  , т.е.
, т.е. 
Если существует конечный предел 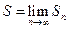 последовательности частичных сумм ряда
последовательности частичных сумм ряда  , то этот предел называют суммой ряда и говорят, что ряд сходится. Записывают:
, то этот предел называют суммой ряда и говорят, что ряд сходится. Записывают: 
Если  не существует или
не существует или  =
=  , то ряд называют расходящимся. Такой ряд суммы не имеет.
, то ряд называют расходящимся. Такой ряд суммы не имеет.
Рассмотрим некоторые важные свойства рядов:
Свойство 1. Если ряд  сходится и его сумма равна S, то ряд
сходится и его сумма равна S, то ряд
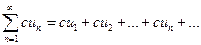
где с – произвольное число, также сходится и его сумма равна cS. Если же ряд  расходится и
расходится и  , то и ряд
, то и ряд 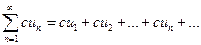 расходится.
расходится.
Обозначим n -ю частичную сумму ряда 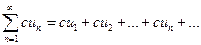 через
через  . Тогда
. Тогда

Следовательно,
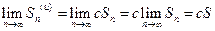 ,
,
т.е. ряд 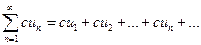 сходится и имеет сумму cS.
сходится и имеет сумму cS.
Покажем теперь, что если ряд  расходится,
расходится,  , то и ряд
, то и ряд 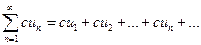 расходится. Допустим противное: ряд
расходится. Допустим противное: ряд 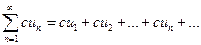 сходится и имеет сумму
сходится и имеет сумму 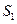 .
.
Тогда 
Отсюда получаем: 
т.е. ряд  сходится, что противоречит условию о расходимости ряда.
сходится, что противоречит условию о расходимости ряда.
Свойство 2. Если сходится ряд  и сходится ряд
и сходится ряд

А их суммы равны 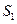 и
и  соответственно, то сходятся и ряды
соответственно, то сходятся и ряды
 ,
,
причем сумма каждого равна соответственно 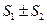 .
.
Обозначим n -е частичные суммы рядов  ,
,  и
и  через
через  ,
,  и
и  соответственно. Тогда
соответственно. Тогда

т.е. каждый из рядов  сходится, и сумма его равна
сходится, и сумма его равна 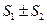 соответственно.
соответственно.
Из свойства 2 вытекает, что сумма (разность) сходящегося и расходящегося рядов есть расходящийся ряд.
Свойство 3. Если к ряду  прибавить (или отбросить) конечное число членов, то полученный ряд и ряд
прибавить (или отбросить) конечное число членов, то полученный ряд и ряд  сходятся или расходятся одновременно.
сходятся или расходятся одновременно.
Обозначим через S сумму отброшенных членов, через k – наибольший из номеров этих членов. Чтобы не менять нумерацию оставшихся членов ряда, будем считать, что на месте отброшенных членов поставили нули. Тогда при n>k будет выполняться равенство  , где
, где  – это n -я частичная сумма ряда, полученного из ряда
– это n -я частичная сумма ряда, полученного из ряда  путем отбрасывания конечного числа членов. Поэтому
путем отбрасывания конечного числа членов. Поэтому
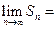
 +
+  . Отсюда следует, что пределы в левой и правой частях одновременно существуют или не существуют, т.е. ряд
. Отсюда следует, что пределы в левой и правой частях одновременно существуют или не существуют, т.е. ряд  сходится (расходится) тогда и только тогда, когда сходятся (расходятся) ряды без конечного числа его членов.
сходится (расходится) тогда и только тогда, когда сходятся (расходятся) ряды без конечного числа его членов.
Аналогично рассуждаем в случае приписывания к ряду конечного числа членов.
Ряд
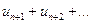 =
= 
называется n -м остатком ряда  . Он получается из ряда отбрасыванием n первых его членов. Ряд
. Он получается из ряда отбрасыванием n первых его членов. Ряд  получается из остатка добавлением конечного числа членов. Поэтому, согласно свойству 3, ряд
получается из остатка добавлением конечного числа членов. Поэтому, согласно свойству 3, ряд  и его остаток
и его остаток 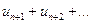 =
= 
одновременно сходятся или расходятся.
Из свойства 3 также следует, что если ряд  сходится, то его остаток
сходится, то его остаток  стремится к нулю при
стремится к нулю при  , т.е.
, т.е. 





 с заданной точностью
с заданной точностью 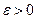
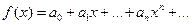
 , то точное значение
, то точное значение  равно сумме этого ряда при
равно сумме этого ряда при 
 , т.е.
, т.е.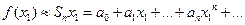
 ,
,
 можно найти, оценив остаток
можно найти, оценив остаток 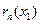 ряда.
ряда.
 с точностью до
с точностью до 
 – действительные или комплексные числа, называемые членами ряда,
– действительные или комплексные числа, называемые членами ряда, 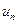 - общим членом ряда.
- общим членом ряда.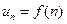 .
. , т.е.
, т.е. 
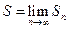 последовательности частичных сумм ряда
последовательности частичных сумм ряда 
 не существует или
не существует или  , то ряд называют расходящимся. Такой ряд суммы не имеет.
, то ряд называют расходящимся. Такой ряд суммы не имеет.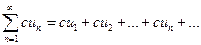
 , то и ряд
, то и ряд  . Тогда
. Тогда
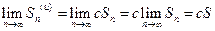 ,
,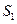 .
.


 соответственно, то сходятся и ряды
соответственно, то сходятся и ряды ,
,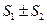 .
. и
и 
 , где
, где  – это n -я частичная сумма ряда, полученного из ряда
– это n -я частичная сумма ряда, полученного из ряда 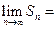
 +
+  . Отсюда следует, что пределы в левой и правой частях одновременно существуют или не существуют, т.е. ряд
. Отсюда следует, что пределы в левой и правой частях одновременно существуют или не существуют, т.е. ряд 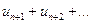 =
= 
 стремится к нулю при
стремится к нулю при  , т.е.
, т.е. 



