Сущность методов этой группы заключается в том, что отклонение рассматриваемого параметра х определяется как сумма предельных отклонений, обусловленных влияниями определяющих параметров x1,x2,...,xn. Пусть Dxmax, Dx1max, Dx2max,..., Dxnmax – предельные положительные, а - Dxmin, -Dx1min,-Dx2min,...,-Dxnmin – предельные отрицательные значения отклонений параметров x1,x2,...,xn.
Предположим, что эти параметрыи их отклонения взаимно независимы и создадим два ряда величин:  и
и  (j =1,2,..., n). Выберем из этих рядов положительные и отрицательные члены и обозначим их соответственно
(j =1,2,..., n). Выберем из этих рядов положительные и отрицательные члены и обозначим их соответственно  и
и 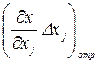 . Тогда в соответствии с рассматриваемым методом, получим
. Тогда в соответствии с рассматриваемым методом, получим
 (1.8)
(1.8)
и
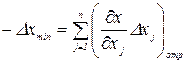 (5.11)
(5.11)
В том случае, если отклонения Dхj параметров хj обусловлены влиянием каких-либо внешних факторов (например, температурой среды), они не могут считаться независимыми случайными величинами. По аналогии с формулами (1.7) в этом случае можно получить
 и
и 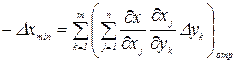
где Dyk – величины отклонений воздействий yk, характеризующиеся предельными положительными Dykmax и отрицательными -Dykmin значениями;

 ,
, 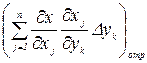 - положительные и отрицательные члены рядов величин
- положительные и отрицательные члены рядов величин  и
и  .
.
Часто на практике отклонения Dxj симметричны (например, производственные допуски на резисторы, на некоторые типы конденсаторов), т.е. Dxjmin=Dxjmax=Dxjд. В этом случае формулы (1.8) и (1.9) приобретают вид
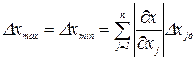 . (1.10)
. (1.10)
Основное достоинство рассматриваемой группы методов заключается в их простоте, благодаря чему они широко используются на практике. Однако эти методы обладают и весьма существенным недостатком: не учитывается случайный характер отклонений отдельных параметров xj, что приводит к завышенным результатам.
Предположим, что все 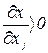 и что возможные отклонения всех параметров величины случайные, принимающие только одно из крайних значений: - Dxjmin или Dxjmax. Первое предположение не влияет на полученные результаты и способствует лишь удобству записи, второе - увеличивает по сравнению с реальными случаями вероятность того, что величины всех параметров xj будут равны их предельным значениям.
и что возможные отклонения всех параметров величины случайные, принимающие только одно из крайних значений: - Dxjmin или Dxjmax. Первое предположение не влияет на полученные результаты и способствует лишь удобству записи, второе - увеличивает по сравнению с реальными случаями вероятность того, что величины всех параметров xj будут равны их предельным значениям.
Ввиду того, что все параметры xj и их отклонения D xj взаимно независимы, вероятность Рпол(Dx1,Dx2,...,Dxn) того, что все отклонения параметров будут положительны, может быть определена по формуле [3]:
 (1.11)
(1.11)
Из анализа полученной формулы следует, что при больших n величина  , определяющая вероятность получения истинного значения Dх весьма мала. Аналогичное заключение можно сделать и в отношении формулы (1.10), а также для всех остальных случаев применения рассматриваемого метода.
, определяющая вероятность получения истинного значения Dх весьма мала. Аналогичное заключение можно сделать и в отношении формулы (1.10), а также для всех остальных случаев применения рассматриваемого метода.
Согласно сделанному предположению для любого n

Пусть для определенности P(Dxj=Dxjmax)=1/2. Тогда на основании формулы (1.11) получим
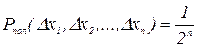 .
.
Отсюда видно, что уже при  совпадение знаков отклонений всех параметров xj является маловероятным. Учитывая сделанное выше предположение о возможных величинах отклонений параметров Dxj, следует признать, что методы рассматриваемой группы дают завышенные величины отклонения Dx.
совпадение знаков отклонений всех параметров xj является маловероятным. Учитывая сделанное выше предположение о возможных величинах отклонений параметров Dxj, следует признать, что методы рассматриваемой группы дают завышенные величины отклонения Dx.





 и
и  (j =1,2,..., n). Выберем из этих рядов положительные и отрицательные члены и обозначим их соответственно
(j =1,2,..., n). Выберем из этих рядов положительные и отрицательные члены и обозначим их соответственно  и
и 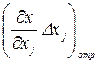 . Тогда в соответствии с рассматриваемым методом, получим
. Тогда в соответствии с рассматриваемым методом, получим (1.8)
(1.8)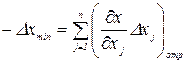 (5.11)
(5.11) и
и 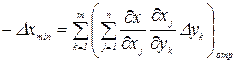

 ,
, 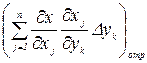 - положительные и отрицательные члены рядов величин
- положительные и отрицательные члены рядов величин  и
и  .
.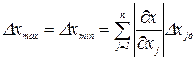 . (1.10)
. (1.10)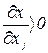 и что возможные отклонения всех параметров величины случайные, принимающие только одно из крайних значений: - Dxjmin или Dxjmax. Первое предположение не влияет на полученные результаты и способствует лишь удобству записи, второе - увеличивает по сравнению с реальными случаями вероятность того, что величины всех параметров xj будут равны их предельным значениям.
и что возможные отклонения всех параметров величины случайные, принимающие только одно из крайних значений: - Dxjmin или Dxjmax. Первое предположение не влияет на полученные результаты и способствует лишь удобству записи, второе - увеличивает по сравнению с реальными случаями вероятность того, что величины всех параметров xj будут равны их предельным значениям. (1.11)
(1.11) , определяющая вероятность получения истинного значения Dх весьма мала. Аналогичное заключение можно сделать и в отношении формулы (1.10), а также для всех остальных случаев применения рассматриваемого метода.
, определяющая вероятность получения истинного значения Dх весьма мала. Аналогичное заключение можно сделать и в отношении формулы (1.10), а также для всех остальных случаев применения рассматриваемого метода.
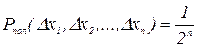 .
. совпадение знаков отклонений всех параметров xj является маловероятным. Учитывая сделанное выше предположение о возможных величинах отклонений параметров Dxj, следует признать, что методы рассматриваемой группы дают завышенные величины отклонения Dx.
совпадение знаков отклонений всех параметров xj является маловероятным. Учитывая сделанное выше предположение о возможных величинах отклонений параметров Dxj, следует признать, что методы рассматриваемой группы дают завышенные величины отклонения Dx.


