Департамент учета, анализа и аудита
Методические указания
К выполнению расчетно-аналитической работы
по дисциплине
СТАТИСТИКА
Раздел: ОБЩАЯ ТЕОРИЯ СТАТИСТИКИ
Для студентов заочной формы обучения по направлениям
38.03.01 - Экономика,
38.03.02 - Менеджмент,
38.03.04 - Государственное и муниципальное управление
(все профили подготовки)
КВАЛИФИКАЦИЯ (СТЕПЕНЬ) "БАКАЛАВР"
Москва – 2016 г.
Учебно-методическая разработка предназначена для студентов бакалавриата заочной формы обучения по направлениям "Менеджмент", "Экономика", "Государственное и муниципальное управление".
Методические указания разработали:
доктор физико-математических наук, профессор Г.П. Кожевникова,
кандидат экономических наук, доцент Л.Ю. Архангельская,
кандидат экономических наук, доцент Т.А. Долбик - Воробей
Ответственный редактор профессор В.Н.Салин
Структура расчетно-аналитической работы
Каждый вариант содержит пять практических заданий:
Задание 1. Исследование структуры изучаемой статистической
совокупности.
Задание 2. Корреляционно-регрессионный анализ взаимосвязи между
признаками совокупности.
Задание 3. Применение выборочного метода в статистическом
исследовании.
Задание 4. Методы анализа рядов динамики в экономических задачах.
Задание 5. Применение индексного метода в анализе статистических
данных.
Содержание заданий
Задания 1 - 3
1. Исходные данные заданий 1 - 3
Имеются следующие выборочные данные за год по предприятиям одной из отраслей экономики региона (выборка 10%-ная механическая):
Таблица 1.1. Исходные данные базового варианта заданий
| № предприятия п/п
| Выручка от продажи продукции, млн руб.
| Прибыль от продажи
продукции, млн руб.
| № предприятия п/п
| Выручка от продажи продукции, млн руб.
| Прибыль от продажи
продукции, млн руб.
|
|
| 250+0,5N
| 80+0,5N
|
| 200+0,5N
| 73+0,5N
|
|
| 170+0,4N
| 54+0,4N
|
| 190+0,4N
| 63+0,4N
|
|
| 200+0,3N
| 70+0,3N
|
| 230+0,3N
| 80+0,3N
|
|
| 290+0,1N
| 83+0,1N
|
| 210+0,2N
| 90+0,2N
|
|
| 190+0,2N
| 65+0,2N
|
| 200+0,1N
| 76+0,1N
|
|
| 200+0,5N
| 75+0,5N
|
| 210+0,5N
| 75+0,5N
|
|
| 200+0,3N
| 80+0,3N
|
| 220+0,4N
| 78+0,4N
|
|
| 190+0,4N
| 68+0,4N
|
| 200+0,2N
| 77+0,2N
|
|
| 260+0,2N
| 85+0,2N
|
| 200+0,3N
| 75+0,3N
|
|
| 260+0,1N
| 80+0,1N
|
| 200+0,1N
| 78+0,1N
|
|
| 230+0,5N
| 81+0,5N
|
| 180+0,5N
| 54+0,5N
|
|
| 190+0,4N
| 60+0,4N
|
| 190+0,4N
| 62+0,4N
|
|
| 230+0,3N
| 80+0,3N
|
| 180+0,3N
| 55+0,3N
|
|
| 200+0,2N
| 70+0,2N
|
| 210+0,2N
| 75+0,2N
|
|
| 210+0,1N
| 75+0,1N
|
| 200+0,1N
| 70+0,1N
|
Исходные данные для индивидуального варианта заданий формируются студентом в табл.1.1 самостоятельно путем увеличения данных базового варианта на величину N= i * к*l, где i - две последние цифры текущего года, к - последние две цифры номера зачетной книжки студента, l -код направления подготовки студента: 1 - экономика, 2 - менеджмент, 3 - государственное и муниципальное управление (при условии N= i * к*l = 0 принять N=100).
Пример.
Для 2016 г. номера зачетной книжки с двумя последними цифрами 10 и направления подготовки "Менеджмент" N = i * к*l = 16*10*2 = 320. Тогда первая строка табл.1.1 имеет вид:
| № предприятия п/п
| Выручка от продажи продукции
| Прибыль от продаж
| № предприятия п/п
| Выручка от продажи продукции
| Прибыль от продаж
|
|
|
|
|
|
|
|
2. Содержание заданий 1 - 3
Задание 1
По исходным данным:
1) постройте статистический интервальный ряд распределения предприятий по признаку «Выручка от продажи продукции», образовав пять групп с равными интервалами;
2) рассчитайте значения моды и медианы полученного интервального ряда распределения;
3) рассчитайте следующие статистические характеристики ряда распределения: среднюю арифметическую, дисперсию, среднее квадратическое отклонение, коэффициент вариации, представив расчеты в табличном виде.
Сделайте выводы по результатам выполнения пунктов 1 - 3.
Задание 2
По исходным данным (табл.1.1) с использованием результатов выполнения задания 1:
1) методом аналитической группировки установите наличие и направление корреляционной связи между факторным признаком Х - «Выручка от продажи продукции» и результативным признаком Y - «Прибыль от продажи продукции»;
2) по исходным данным постройте линейную однофакторную регрессионную модель зависимости признака Y от фактора Х;
3) проверьте найденную модель на адекватность;
4) рассчитайте средний коэффициент эластичности взаимосвязи признаков.
Сделайте выводы по результатам выполнения задания.
Задание 3
По результатам выполнения задания 1 с вероятностью 0,954 определите:
1) ошибку выборки средней величины выручки от продажи продукции и границы, в которых будет находиться средняя величина выручки предприятий генеральной совокупности.
2) ошибку выборки доли предприятий с выручкой от продажи продукции более  млн. руб. (
млн. руб. ( - средняя величина выручки рассчитанная в задании 1), а также границы, в которых будет находиться генеральная доля.
- средняя величина выручки рассчитанная в задании 1), а также границы, в которых будет находиться генеральная доля.
Задание 4
4. 1. Исходные данные задания 4
Исходные данные базового варианта задания представлены в табл. 4.1.
Таблица 4.1
ЗАДАНИЕ 5
Задание 5 носит комплексный характер и включает 3 задачи. Индивидуальный вариант исходных данных задач формируется студентом самостоятельно с учетом рассчитанной ранее величины N= i * к*l.
Задача 5.1
Имеются данные о продаже условного товара "А" в магазинах города в третьем и четвертом кварталах(табл.5.1).
Таблица 5.1
Исходные данные
| Форма торговли
| Объем продаж, тыс.кг
| Цена за 1 кг
|
|
| III квартал
| IV квартал
| III квартал
| VI квартал
|
| Сетевая
| 4+0,4*N
| 5+0,3*N
|
|
|
| Несетевая
| 5+0,2*N Абсолютный прирост средней себестоимости за счет двух факторов
| 6+0,1*N
|
|
|
Определите:
1. По каждой форме торговли относительные изменения
(индивидуальные индексы):
- цен,
- физического объема продажи (в натуральном выражении).
2. В целом по двум формам торговли относительные изменения (общие индексы):
- цен (в форме Пааше),
- физического объема продажи (в форме Ласпейреса),
- товарооборота (в стоимостном выражении).
Покажите взаимосвязь между этими индексами.
3. Абсолютное изменение товарооборота - общее и в результате
влияния отдельных факторов (изменения цен и изменения
физического объема продаж).
4. Индексы средней цены товара "А" переменного и постоянного состава,
индекс влияния структурных сдвигов в объеме продаж.
Покажите взаимосвязь индексов переменного, постоянного состава
и структурных сдвигов.
5. Изменение средней цены товара "А" в абсолютном выражении и
влияние на это изменение двух факторов:
а) изменение цен,
б) изменение структуры объемов продажи.
Результаты промежуточных расчетов представьте в табличной форме.
Сделайте выводы.
Задача 5.2
Имеются данные о продаже двух видов условного товара (табл.5.2).
Требуется определить относительное изменение физического объема товарооборота в целом по двум видам товара (с использованием среднего арифметического взвешенного индекса физического объема).
Таблица 5.2
Исходные данные
| Вид товара
| Единица измерения
| Товарооборот базисного периода, млн. руб.
| Относительное изменение количества реализованного товара в отчетном периоде по сравнению с базисным (+,-), %
|
|
|
|
|
|
| А
| шт.
| 6,0+0,3N
| +66,7
|
| Б
| м
| 12,0+0,1N
| -37,5
|
Задача 5.3
Имеются данные о продаже двух видов условного товара (табл.5.3).
Требуется определить относительное изменение уровня цен в целом по двум видам товара (с использованием среднего гармонического взвешенного индекса цен).
Таблица 5.3
Исходные данные
| Вид товара
| Единица измерения
| Товарооборот отчетного периода, млн. руб.
| Относительное изменение цен (+,-), %
|
|
|
|
|
|
| А
| шт
| 11,0+0,3N
| +10,0
|
| Б
| м
| 10,0+0,1N
| +33,3
|
Задание 4.1. Расчёт и анализ основных показателей ряда динамики.
Исходные данные варианта задания представлены в табл. 4.1,
Таблица 4.1
Задание 4.2. Расчёт и анализ средних показателей ряда динамики
1. Среднегодовой объем реализации продукции:

2.Среднегодовой абсолютный прирост объемов реализации продукции:

3. Среднегодовой темп роста объемов реализации продукции:

4. Среднегодовой темп прироста объемов реализации продукции:

Вывод. За исследуемый период средний объем реализации произведенной продукции составил 24 441,3 тыс. тонн. Выявлена положительная динамика реализации продукции: ежегодное увеличение объема реализации составляло в среднем  тыс. тонн или 8,4%.
тыс. тонн или 8,4%.
График динамики объемов реализации продукции представлен на рис.4.1.

Рис. 4.1. Динамика объемов реализации продукции за пятилетний период
.
Задание 4.3. Выявление тенденции развития изучаемого явления
1. Сглаживание ряда динамики методом укрупнения интервалов
Результаты представлены в табл.4.3.
Таблица 4.3.
Расчётная таблица для определения укрупнённых (поквартальных) данных
| Месяцы
| Объем реализации продукции, тыс. тонн
| Кварталы
| Объем реализации продукции, тыс. тонн
| Среднемесячный объем реализации продукции, тыс. тонн
| |
| |
| |
| январь
| 2 435,0
| первый
| 5421,0
| 1807,0
| |
| февраль
| 1 375,1
| |
| март
| 1 610,9
| |
| апрель
| 2 211,6
| второй
| 7612,6
| 2537,5
| |
| май
| 2 563,1
| |
| июнь
| 2 837,9
| |
| июль
| 3 040,9
| третий
| 9543,4
| 3181,1
| |
| август
| 3 488,2
| |
| сентябрь
| 3 014,3
| |
| октябрь
| 2 637,7
| четвёртый
| 7266,4
| 2422,1
| |
| ноябрь
| 2 328,4
| |
| декабрь
| 2 300,3
| |
| Итого
| 29 843,4
| Итого
| 29 843,4
| 2487,0
| |
Вывод. Данные табл. 4.3 показывают, что в результате применения метода укрупнения интервалов проявилось общее направление (тренд) изменения объема реализации продукции: в первых трех кварталах среднемесячные объемы реализации продукции возрастали, а в четвертом существенно снизились.
2. Сглаживание ряда динамики методом скользящих средних
Результаты представлены в табл.4.4.
Таблица 4.4
Расчётная таблица для определения значений скользящей средней
| Месяцы
| Объем реализации продукции, тыс. тонн
| Скользящая трехзвенная сумма, тыс. тонн
| Скользящая средняя, тыс. тонн
|
| январь
| 2 435,00
| -
| -
|
| февраль
| 1 375,10
| 5 421,00
| 1807,0
|
| март
| 1 610,90
| 5 197,60
| 1732,5
|
| апрель
| 2 211,60
| 6 385,60
| 2128,5
|
| май
| 2 563,10
| 7 612,60
| 2537,5
|
| июнь
| 2 837,90
| 8 441,90
| 2814,0
|
| июль
| 3 040,90
| 9 367,00
| 3122,3
|
| август
| 3 488,20
| 9 543,40
| 3181,1
|
| сентябрь
| 3 014,30
| 9 140,20
| 3046,7
|
| октябрь
| 2 637,70
| 7 980,40
| 2660,1
|
| ноябрь
| 2 328,40
| 7 266,40
| 2422,1
|
| декабрь
| 2 300,30
| -
| -
|
| Итого
| 29 843,4
| -
| -
|
Вывод. Как показывают данные табл.4.4, значения скользящей средней до сентября месяца почти систематически возрастали, а затем стали снижаться, что свидетельствует об общей параболической тенденции изменения объемов реализации продукции. Поскольку большая часть параболы близка к прямолинейной форме (7 значений скользящей средней из 10-ти систематически возрастают), для сглаживания ряда динамики может быть использовано выравнивание ряда по прямой (а не по параболе).
3. Аналитическое выравнивание ряда динамики по прямой
3.1.Аналитическое уравнение прямой имеет вид:

где t – порядковый номер периодов (или моментов) времени;
 – выровненные значения ряда динамики.
– выровненные значения ряда динамики.
Отсчёт времени удобно производить так, чтобы сумма показателей времени ряда динамики была равна нулю[3]:

При соблюдении принципа отсчёт а времени t от условного нулевого начала система нормальных уравнений имеет вид:


параметры уравнения определяются по формулам:
 ,
, 
Расчет значений величин  ,
,  и
и  приведен в табл.4.5
приведен в табл.4.5
Таблица 4.5
Расчетная таблица для определения параметров 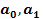 уравнения прямой
уравнения прямой
| Месяц
| Объем реализации, тыс. тонн,

| Условное обозначение периодов,

| 
| 
| Выровненные уровни ряда динамики,
тыс. тонн

|
|
|
|
|
|
|
|
| январь
| 2 435,00
| -11
| -26785
|
| 2077,769231
|
| февраль
| 1 375,10
| -9
| -12375,9
|
| 2152,165734
|
| март
| 1 610,90
| -7
| -11276,3
|
| 2226,562238
|
| апрель
| 2 211,60
| -5
| -11058
|
| 2300,958741
|
| май
| 2 563,10
| -3
| -7689,3
|
| 2375,355245
|
| июнь
| 2 837,90
| -1
| -2837,9
|
| 2449,751748
|
| июль
| 3 040,90
|
| 3040,9
|
| 2524,148252
|
| август
| 3 488,20
|
| 10464,6
|
| 2598,544755
|
| сентябрь
| 3 014,30
|
| 15071,5
|
| 2672,941259
|
| октябрь
| 2 637,70
|
| 18463,9
|
| 2747,337762
|
| ноябрь
| 2 328,40
|
| 20955,6
|
| 2821,734266
|
| декабрь
| 2 300,30
|
| 25303,3
|
| 2896,130769
|
| Итого
| 29 843,40
|
| 21277,4
|
| 29843,40000
|
Использование итоговых данных гр. 2-5 табл.4.5 дает систему нормальных уравнений


Из 1-го уравнения определяется значение  , из 2-го -
, из 2-го - 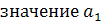 :
:
 = 2486,95
= 2486,95  = 37,20
= 37,20
Вывод. Уравнение прямой для сглаживания динамического ряда:

3.2. Проверка правильности расчёта уровней выровненного ряда динамики (сумма значений уровней эмпирического ряда (гр.2) должна совпадать с суммой значений уровней выровненного ряда (гр.6) или незначительно расходиться с ней.)
В расчетах наблюдается совпадение сумм: 29 843,4 = 29 843,4
3.3. Графики эмпирической и сглаживающей кривых представлены на рис.4.2.

Рис. 4.2. Сглаживание ряда динамики объемов реализации продукции методом аналитического выравнивания по прямой
4.4. Прогнозирование значений показателей методом экстраполяции [4]
1. Прогнозирование уровня ряда динамики с использованием среднего абсолютного прироста осуществляется по следующей формуле:

где:  – прогнозируемый уровень;
– прогнозируемый уровень;
t – период упреждения (число лет, кварталов и т.п.);
 – конечный уровень исследуемого ряда динамики;
– конечный уровень исследуемого ряда динамики;
 – средний за исследуемый период абсолютный прирост (среднегодовой, среднеквартальный и т.п.).
– средний за исследуемый период абсолютный прирост (среднегодовой, среднеквартальный и т.п.).
Прогнозируемый объем реализации продукции на 7 год (по данным пятилетнего периода) с использованием среднего абсолютного прироста, рассчитанного в задании 4.2:

2. Прогнозирование уровня ряда динамики с использованием среднего темпа (коэффициента) роста осуществляется по следующей формуле:

где 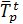 – средний за исследуемый период темп роста (среднегодовой, среднеквартальный и т.п.).
– средний за исследуемый период темп роста (среднегодовой, среднеквартальный и т.п.).
Прогнозируемый объем реализации продукции на седьмой год (по данным пятилетнего периода) с использованием среднего темпа роста, рассчитанного в задании 2:

3. Прогнозирование объемов реализации продукции методом аналитического выравнивания ряда динамики по прямой
Модель прямолинейной зависимости уровня ряда от фактора времени имеет следующий вид:

Параметры уравнения a и b определяются путем решения системы нормальных уравнений:


Расчет значений величин  ,
, 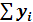 ,
,  и
и  приведен в табл.4.6.
приведен в табл.4.6.
Таблица 4.6
Вспомогательная таблица для расчёта параметров тренда
| год
| Объем реализации, тыс. тонн,

| Условное обозначение периодов,

| 
| 
| Выровненные уровни ряда динамики,
тыс. тонн

| |
| |
|
|
|
|
|
|
| |
| 1-й
| 21584,7
|
| 21584,7
|
| 20866,22
| |
| 2-й
| 22887,9
|
| 45775,8
|
| 22653,76
| |
| 3-й
| 23644,6
|
| 70933,8
|
| 24441,30
| |
| 4-й
| 24245,9
|
| 96983,6
|
| 26228,84
| |
| 5-й
| 29843,4
|
| 149217,0
|
| 28016,38
| |
| Итого
|
122206,5
|
| 384494,9
|
| 122206,5
| |
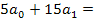 122206,5
122206,5

По системе уравнений определяем значение параметров 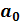 и
и  , уравнение прямой имеет вид:
, уравнение прямой имеет вид:

Расчет теоретических уровней приведен в гр.6.
Совпадение итоговых значений гр.2 и 6 указывает на правильность расчётов уровней выровненного ряда динамики.
Прогнозируемый объем реализации продукции на 7 год (по данным пятилетнего периода) методом аналитического выравнивания ряда динамики по прямой:
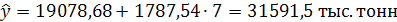
Вывод. Как показывают полученные прогнозные данные, все прогнозируемые объемы реализации продукции на 7 год (по данным пятилетнего периода) довольно близки между собой: 33972,8, 35067,7 и 31591,5  тыс. тонн. Расхождение полученных данных объясняется тем, что в основу прогнозирования положены разные методики экстраполяции рядов динамики.
тыс. тонн. Расхождение полученных данных объясняется тем, что в основу прогнозирования положены разные методики экстраполяции рядов динамики.
Задача 5.1
Имеются данные о продаже условного товара "А" в магазинах города в третьем и четвертом кварталах(табл.5.1).
Таблица 5.1
Исходные данные
| Форма торговли
| Объем продаж, тыс.кг
| Цена за 1 кг
|
|
| III квартал
| IV квартал
| III квартал
| VI квартал
|
| Сетевая
| 4+0,4N
| 5+0,3N
|
|
|
| Несетевая
| 5 +0,2N Абсолютный прирост средней себестоимости за счет двух факторов
| 6+0,1N
|
|
|
Определите:
3. По каждой форме торговли относительные изменения
(индивидуальные индексы):
- цен,
- физического объема продажи (в натуральном выражении).
4. В целом по двум формам торговли относительные изменения (общие индексы):
- цен (в форме Пааше),
- физического объема продажи (в форме Ласпейреса),
- товарооборота (в стоимостном выражении).
Покажите взаимосвязь между этими индексами.
3. Абсолютное изменение товарооборота - общее и в результате
влияния отдельных факторов (изменения цен и изменения
физического объема продаж).
4. Индексы средней цены товара "А" переменного и постоянного состава,
индекс влияния структурных сдвигов в объеме продаж.
Покажите взаимосвязь индексов переменного, постоянного состава
и структурных сдвигов.
5. Изменение средней цены товара "А" в абсолютном выражении и
влияние на это изменение двух факторов: а) изменение цен,
б) изменение структуры объемов продажи.
Результаты промежуточных расчетов представьте в табличной форме.
Сделайте выводы.
1. Расчет индивидуальных индексов
1.1 Для определения относительного изменения цены товара (p) по каждой форме торговли необходимо рассчитать индивидуальные индексы цен (ip) по формуле
 , (5.1)
, (5.1)
где p0 и p1 – цена товара в базисном и отчетном периодах.
Расчет индивидуальных индексов цен по формуле (5.1):
- сетевая торговля: 
- несетевая торговля:  166,7%
166,7%
Вывод. В сетевой торговле цена на товар «А » выросла в IV кв. по сравнению с III кв. на 75% (175-100), что в абсолютном выражении составляет 30 руб.(70-40), в несетевой - на 67% или на 20 руб..
1.2. Для определения относительного изменения объема продажи товара (q) необходимо рассчитать индивидуальные индексы физического объема (iq) по формуле

где q0 и q1 – количество (физический объем) товара, реализованного в базисном и отчетном периодах.
Расчет индивидуальных индексов физического объема по формуле (5.2):
- сетевая торговля: 
- несетевая торговля: 
Вывод. В сетевой торговле объем продажи товара «А» вырос в IV кв. по сравнению с III кв. на 25% (125-100), что в абсолютном выражении составляет 1 тыс.кг, в несетевой - на 20% или на 1 тыс.кг.
2. Расчет общих индексов относительного изменения товарооборота
Для расчета общих индексов сформируем табл.5.2. В графах 2 - 5 запишем исходные данные, в графах 6 и 7 - рассчитанные индивидуальные индексы, в графах 8 - 11 - товарооборот в разных периодах.
Таблица 5.2
Расчетная таблица
| Форма торговли
| Объем продажи,
тыс. кг
| Цена товара, руб.
| Индивидуальный индекс цен,
%
| Индивидуальный индекс физического объема %
| Товарооборот, тыс. руб.
|
| базисный период III кв.
| отчетный период IV кв.
| базисный период III кв.
| отчетный период IV кв.
| базисный период
| отчетный период
| отчетный период по ценам базисного
| базисный период по ценам отчетного
|

| 
| 
| 
| 
| 
| 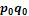
| 
| 
| 
|
|
|
|
|
|
| 6=3:2
*100
| 7=5:4
*100
| 8=4∙2
| 9=3∙5
| 10=4∙3
| 11=5∙2
|
| сетевая
|
|
|
|
| 175,0
| 125,0
|
|
|
|
|
| несетевая
|
|
|
|
| 166,7
| 120,0
|
|
|
|
|
| Итого
|
|
| -
| -
| -
| -
|
|
|
|
|
2.1. Расчет общего индекса цен.
Индекс цен, характеризующий относительное изменение товарооборота под влиянием изменения цен, рассчитывается по формуле

Расчет общего индекса цен по формуле  :
:

Вывод. В целом по двум формам торговли цена товара возросла в IV кв. по сравнению с III кв. в среднем на 71,1%. Абсолютная сумма перерасхода денежных средств населения в результате повышения цены товара "А" составляет 270 тыс.руб. (650 - 380).
2.2. Расчет общего индекса физического объема продаж.
Индекс физического объема продаж, показывающий относительное изменение товарооборота под влиянием изменения объема продаж, рассчитывается по формуле

Расчет общего индекса физического объема продаж по формуле  :
:
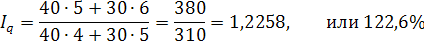
Вывод. В целом по двум формам торговли объем продаж товара возрос
в IV кв. по сравнению с III кв. в среднем на 22,6%.
2.3. Расчет общего индекса товарооборота.
Индекс товарооборота, характеризующий относительное изменение товарооборота под влиянием изменения двух факторов - цен и физического объема продаж, рассчитывается по формуле
 (5.5)
(5.5)
Расчет общего индекса товарооборота по формуле s w:val="28"/></w:rPr><m:t>:</m:t></m:r></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>"> 

Вывод: в целом по двум формам торговли товарооборот в IV кв. по сравнению с III кв. в результате изменения цен и физического объема продаж увеличился на 109,7 %, что в абсолютном выражении составляет 340 тыс. руб.
2.4. Взаимосвязь индексов и разложение изменения товарооборота по факторам
Произведение индекса физического объема и индекса цен должно давать индекс изменения товарооборота (мультипликативная связь), т.е.
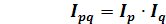 (5.6)
(5.6)
Эта формула называется факторной моделью индекса товарооборота. Она показывает изменение товарооборота за счёт изменения цен и за счёт изменения объема продаж.
Разложение относительного изменения товарооборота по факторам:

Вывод. В целом по двум формам торговли увеличение товарооборота в
2,097 раз произошло за счет роста цены товара в 1,711 раза и роста объема продаж в 1,226 раза.
3. Определение абсолютного изменения товарооборота.
Общее абсолютное изменение товарооборота в отчетном периоде по сравнению с базисным (под влиянием обоих факторов) определяется какразностьмежду числителем и знаменателем индекса товарооборота (5.5):
 (5.7)
(5.7)
Разность между числителем и знаменателем индекса цен (5.3) характеризует абсолютное изменение товарооборота в отчетном периоде по сравнению с базисным в результате изменения цен:
 (5.8)
(5.8)
Разность между числителем и знаменателем индекса физического объемапродаж (5.4) характеризует общее абсолютное изменение товарооборота в отчетном периоде по сравнению с базисным в результате изменения физического объема продаж:
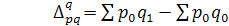 (5.9)
(5.9)
Взаимосвязь абсолютных приростов (аддитивная связь):
 (5.10)
(5.10)
Эта формула называется аддитивноймоделью индекса товарооборота. Она показывает абсолютное изменение товарооборота за счёт изменения цен и за счёт изменения объема продаж.
3.1. Расчет абсолютного изменения товарооборота в отчетном периоде по сравнению с базисным:
- общего абсолютного изменения по формуле (5.7):

- под влиянием изменения цен по формуле (5.8):
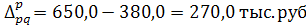
- под влиянием изменения физического объема продаж по формуле (5.9):

3.2. Разложение абсолютных приростов товарооборота по факторам (5.10):

Вывод. В целом по двум формам торговли товарооборот в IV кв. по сравнению с III кв. под влиянием изменения цены товара (на 71,1%) вырос в среднем на  Рост физического объема продаж на 22,6% привел к увеличению товарооборота в среднем н
Рост физического объема продаж на 22,6% привел к увеличению товарооборота в среднем н  Совместное влияние двух факторов выразилось в росте общего товарооборота в среднем на
Совместное влияние двух факторов выразилось в росте общего товарооборота в среднем на  . (на 109,7%).
. (на 109,7%).
Задача 5.2
Исходная информация представлена в табл.5.4. Требуется определить
относительное изменение физического объема товарооборота в целом по
двум видам товара.
Таблица 5.4
Исходные данные
| Вид товара
| Единица измерения
| Товарооборот базисного периода, млн. руб.
| Относительное изменение количества реализованного товара в отчетном периоде по сравнению с базисным (+,-), %
|
|
|
|
|
|
| А
| шт.
| 6,0+0,3N
| +66,7
|
| Б
| м
| 12,0+0,1N
| -37,5
|
Для определения относительного изменения физического объема товарооборота обычно рассчитывают агрегатный индекс физического объема товарооборота 
 .
.
Однако, по приведенной в табл.5. 4 исходной информации этого сделать нельзя, так как неизвестен товарооборот отчетного периода в базисных ценах (числитель индекса  ). Он может быть рассчитан на основе данных гр. 4 с использованием преобразования агрегатного индекса физического объема в средний арифметический взвешенный:
). Он может быть рассчитан на основе данных гр. 4 с использованием преобразования агрегатного индекса физического объема в средний арифметический взвешенный:

Для преобразования используют формулу индивидуального индекса физического объема[5], получая средний арифметический взвешенный индекс физического объема товарооборота (5.21 ):
 (5.21)
(5.21)
где  – индивидуальный индекс физического объема;
– индивидуальный индекс физического объема;
 – стоимость реализованных товаров (товарооборот) в базисном периоде.
– стоимость реализованных товаров (товарооборот) в базисном периоде.
1. Расчет индивидуальных индексов физического объема (количества) реализованного товара:
Товар А:  s w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>i</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>q</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
s w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>i</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>q</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  =100+66,7=166,7 %, или 1,667;
=100+66,7=166,7 %, или 1,667;
Товар В:  = 100-37,5=62,5%, или 0,625
= 100-37,5=62,5%, или 0,625
(результаты расчетов представлены в расчетной табл.5.5, гр.4, 5).
Таблица 5.5
Расчетная таблица
| Товар
| Единица измерения
| Товарооборот базисного периода, млн. руб.
| Индекс физического объема
| Товарооборот отчетного периода в ценах базисного периода, млн. руб.
|

| 
| 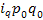
|
|
|
|
|
| 5=3*4
|
| А
Б
| шт.
м
| 6,0
12,0
| 1,667
0,625
| 10,0
7,5
|
| Итого
| 18,0
| 0,972
| 17,5
|
2. Расчет среднего





 млн. руб. (
млн. руб. ( - средняя величина выручки рассчитанная в задании 1), а также границы, в которых будет находиться генеральная доля.
- средняя величина выручки рассчитанная в задании 1), а также границы, в которых будет находиться генеральная доля.



 тыс. тонн или 8,4%.
тыс. тонн или 8,4%.

 – выровненные значения ряда динамики.
– выровненные значения ряда динамики.


 ,
, 
 ,
,  и
и  приведен в табл.4.5
приведен в табл.4.5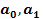 уравнения прямой
уравнения прямой






 , из 2-го -
, из 2-го - 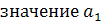 :
: = 2486,95
= 2486,95  = 37,20
= 37,20


 – прогнозируемый уровень;
– прогнозируемый уровень; – конечный уровень исследуемого ряда динамики;
– конечный уровень исследуемого ряда динамики; – средний за исследуемый период абсолютный прирост (среднегодовой, среднеквартальный и т.п.).
– средний за исследуемый период абсолютный прирост (среднегодовой, среднеквартальный и т.п.).

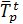 – средний за исследуемый период темп роста (среднегодовой, среднеквартальный и т.п.).
– средний за исследуемый период темп роста (среднегодовой, среднеквартальный и т.п.).



 ,
, 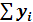 ,
,  и
и  приведен в табл.4.6.
приведен в табл.4.6.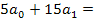 122206,5
122206,5
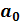 и
и  , уравнение прямой имеет вид:
, уравнение прямой имеет вид:
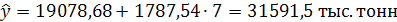
 тыс. тонн. Расхождение полученных данных объясняется тем, что в основу прогнозирования положены разные методики экстраполяции рядов динамики.
тыс. тонн. Расхождение полученных данных объясняется тем, что в основу прогнозирования положены разные методики экстраполяции рядов динамики. , (5.1)
, (5.1)
 166,7%
166,7%








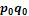




 :
:

 :
: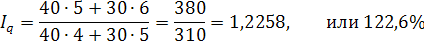
 (5.5)
(5.5)

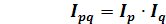 (5.6)
(5.6)
 (5.7)
(5.7) (5.8)
(5.8)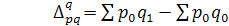 (5.9)
(5.9) (5.10)
(5.10)
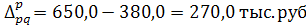


 Рост физического объема продаж на 22,6% привел к увеличению товарооборота в среднем н
Рост физического объема продаж на 22,6% привел к увеличению товарооборота в среднем н  Совместное влияние двух факторов выразилось в росте общего товарооборота в среднем на
Совместное влияние двух факторов выразилось в росте общего товарооборота в среднем на  . (на 109,7%).
. (на 109,7%).
 .
. ). Он может быть рассчитан на основе данных гр. 4 с использованием преобразования агрегатного индекса физического объема в средний арифметический взвешенный:
). Он может быть рассчитан на основе данных гр. 4 с использованием преобразования агрегатного индекса физического объема в средний арифметический взвешенный:
 (5.21)
(5.21) – индивидуальный индекс физического объема;
– индивидуальный индекс физического объема; – стоимость реализованных товаров (товарооборот) в базисном периоде.
– стоимость реализованных товаров (товарооборот) в базисном периоде. s w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>i</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>q</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">
s w:val="28"/><w:lang w:val="EN-US"/></w:rPr><m:t>i</m:t></m:r></m:e><m:sub><m:r><w:rPr><w:rFonts w:ascii="Cambria Math" w:h-ansi="Cambria Math"/><wx:font wx:val="Cambria Math"/><w:i/><w:sz w:val="28"/><w:sz-cs w:val="28"/></w:rPr><m:t>q</m:t></m:r></m:sub></m:sSub></m:oMath></m:oMathPara></w:p><w:sectPr wsp:rsidR="00000000"><w:pgSz w:w="12240" w:h="15840"/><w:pgMar w:top="1134" w:right="850" w:bottom="1134" w:left="1701" w:header="720" w:footer="720" w:gutter="0"/><w:cols w:space="720"/></w:sectPr></w:body></w:wordDocument>">  =100+66,7=166,7 %, или 1,667;
=100+66,7=166,7 %, или 1,667;