Уравнения, содержащие неизвестное под знаком абсолютной величины, можно свести к уравнениям, не содержащим знака абсолютной величины, используя определение модуля. Так, например, решение уравнения
 (21)
(21)
сводится к решению двух уравнений с дополнительными условиями.
1) Если  , то уравнение (21) приводится к виду
, то уравнение (21) приводится к виду
 . (22)
. (22)
Решения этого уравнения:  ,
,  . Условию
. Условию  удовлетворяет второй корень квадратного уравнения (22), и число 3 является корнем уравнения (21).
удовлетворяет второй корень квадратного уравнения (22), и число 3 является корнем уравнения (21).
2) Если  , уравнение (21) приводится к виду
, уравнение (21) приводится к виду
 .
.
Корнями этого уравнения будут числа  и
и  . Первый корень
. Первый корень 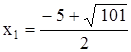 не удовлетворяет условию
не удовлетворяет условию  и поэтому не является решением данного уравнения (21).
и поэтому не является решением данного уравнения (21).
Таким образом, решениями уравнения (21) будут числа 3 и  .
.
Заметим, что коэффициенты уравнения, содержащего неизвестное под знаком абсолютной величины, можно подобрать таким образом, что решениями уравнения будут все значения неизвестного, принадлежащие некоторому промежутку числовой оси. Например, решим уравнение
 . (23)
. (23)
Рассмотрим числовую ось Ох и отметим на ней точки 0 и 3 (ноли функций, стоящих под знаком абсолютной величины). Эти точки разобьют числовую ось на три промежутка (рис. 1):
 ,
,  ,
,  .
.
0 3 x
рис. 1.
1) При  уравнение (23) приводится к виду
уравнение (23) приводится к виду
 .
.
В промежутке  последнее уравнение решений не имеет.
последнее уравнение решений не имеет.
Аналогично, при  уравнение (23) приводится к виду
уравнение (23) приводится к виду

и в промежутке 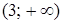 решений не имеет.
решений не имеет.
2) При  уравнение (23) приводится к виду
уравнение (23) приводится к виду
 ,
,
т. е. обращается в тождество. Следовательно, любое значение  является решением уравнения (23).
является решением уравнения (23).
Трансцендентные уравнения
Уравнение, не сводящееся к алгебраическому уравнению с помощью алгебраических преобразований, называется трансцендентным уравнением [4]).
Простешими трансцендентными уравнениями являются показательные, логарифмические и тригонометрические уравнения.

Показательные уравнения
Показательным уравнением называется уравнение, в котором неизвестное входит только в показатели степеней при некоторых постоянных основаниях.
Простейшим показательным уравнением, решение которого сводится к решению алгебраического уравнения, является уравнение вида
 , (24)
, (24)
где  и
и  - некоторые положительные числа
- некоторые положительные числа  . Показательное уравнение (24) эквивалентно алгебраическому уравнению
. Показательное уравнение (24) эквивалентно алгебраическому уравнению
 .
.
В простейшем случае, когда  , показательное уравнение (24) имеет решение
, показательное уравнение (24) имеет решение

Множество решений показательного уравнения вида
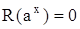 , (25)
, (25)
где  - некоторый многочлен, находится следующим образом.
- некоторый многочлен, находится следующим образом.
Вводится новая переменная  , и уравнение (25) решается как алгебраическое относительно неизвестного
, и уравнение (25) решается как алгебраическое относительно неизвестного  . После этого решение исходного уравнения (25) сводится к решению простейших показательных уравнений вида (24).
. После этого решение исходного уравнения (25) сводится к решению простейших показательных уравнений вида (24).
П р и м е р 1. Решить уравнение
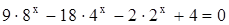 .
.
Записывая уравнение в виде

и вводя новую переменную  , получаем кубическое уравнение относительно переменной
, получаем кубическое уравнение относительно переменной  :
:
 .
.
Нетрудно убедиться, что данное кубическое уравнение имеет единственный рациональный корень  и два иррациональных корня:
и два иррациональных корня:  и
и  .
.
Таким образом, решение исходного уравнения сведено к решению простейших показательных уравнений:
 ,
,  ,
, 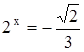 .
.
Последнее из перечисленных, уравнений решений не имеет. Множество решений первого и второго уравнений:
 и
и 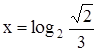 .
.
Н е к о т о р ы е п р о с т е й ш и е п о к а з а т е л ь н ы е у р а в н е н и я:
1) Уравнение вида

заменой  сводится к квадратному уравнению
сводится к квадратному уравнению
 .
.
2) Уравнение вида

заменой  сводится к квадратному уравнению
сводится к квадратному уравнению
 .
.
3) Уравнение вида

заменой  сводится к квадратному уравнению
сводится к квадратному уравнению
 .
.
Логарифмические уравнения
Логарифмическим уравнением называется уравнение, в котором неизвестное входит в виде аргумента логарифмической функции.
Простейшим логарифмическим уравнением является уравнение вида
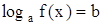 , (26)
, (26)
где  - некоторое положительно число, отличное от единицы,
- некоторое положительно число, отличное от единицы,  - любое действительное число. Логарифмическое уравнение (26) эквивалентно алгебраическому уравнению
- любое действительное число. Логарифмическое уравнение (26) эквивалентно алгебраическому уравнению
 .
.
В простейшем случае, когда  , логарифмическое уравнение (26) имеет решение
, логарифмическое уравнение (26) имеет решение
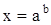 .
.
Множество решений логарифмического уравнения вида  , где
, где  - некоторый многочлен указанного неизвестного, находится следующим образом.
- некоторый многочлен указанного неизвестного, находится следующим образом.
Вводится новая переменная  , и уравнение (25) решается как алгебраическое уравнение относительно
, и уравнение (25) решается как алгебраическое уравнение относительно  . После этого решаются простейшие логарифмические уравнения вида (25).
. После этого решаются простейшие логарифмические уравнения вида (25).
П р и м е р 1. Решить уравнение
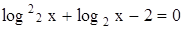 . (27)
. (27)
Относительно неизвестного  данное уравнение – квадратное:
данное уравнение – квадратное:
 .
.
Корни этого уравнения:  ,
,  .
.
Решая логарифмические уравнения
 ,
,  ,
,
получаем решения логарифмического уравнения (27):  ,
,  .
.
В некоторых случаях, для того чтобы свести решение логарифмического уравнения к последовательному решению алгебраического и простейших логарифмических уравнений, необходимо предварительно сделать подходящие преобразования логарифмов, входящих в уравнение. Такими преобразованиями могут быть преобразование суммы логарифмов двух величин в логарифм произведения этих величин, переход от логарифма с одним основанием к логарифму с другим основанием и т. д.
П р и м е р 2. Решить уравнение
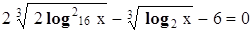 . (28)
. (28)
Для того чтобы свести решение данного уравнения к последовательному решению алгебраического и простейших логарифмических уравнений, необходимо прежде всего привести все логарифмы к одному основанию (здесь, например, к основанию 2). Для этого воспользуемся формулой
 ,
,
в силу которой 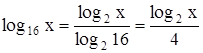 . Подставив в уравнение (28) вместо
. Подставив в уравнение (28) вместо  равную ему величину
равную ему величину  , получаем уравнение
, получаем уравнение

 .
.
Заменой  это уравнение сводится к квадратному уравнению относительно неизвестного
это уравнение сводится к квадратному уравнению относительно неизвестного  :
:
 .
.
Корни этого квадратного уравнения:  ,
,  . Решаем уравнения
. Решаем уравнения  и
и  :
:


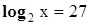
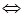
 ,
,

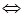


 ,
,
П р и м е р 3. Решить уравнение
 .
.
Преобразуя разность логарифмов двух величин в логарифм частного этих величин:
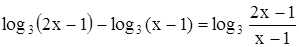 ,
,
сводим данное уравнение к простейшему логарифмическому уравнению




 .
.
Заключение
Математика, как и любая другая наука не стоит на месте, вместе с развитием общества меняются и взгляды людей, возникают новые мысли и идеи. И XX век не стал в этом смысле исключением. Появление компьютеров внесло свои корректировки в способы решения уравнений и значительно их облегчило. Но компьютер не всегда может быть под рукой (экзамен, контрольная), поэтому знание хотя бы самых главных способов решения уравнений необходимо знать. Использование уравнений в повседневной жизни – редкость. Они нашли свое применение во многих отраслях хозяйства и практически во всех новейших технологиях.
В данной работе были представлены далеко не все, способы решения уравнений и даже не все их виды, а только самые основные. Я надеюсь, что мое сочинение может послужить неплохим справочным материалом при решении тех или иных уравнений. В заключении хотелось бы отметить, что при написании данного сочинения я не ставил себе цели показать все виды уравнений, а излагал лишь имеющийся у меня материал.
Список использованной литературы
Глав. ред. М. Д. Аксенова. Энциклопедия для детей. Том 11. Математика. – М.: Аванта+, 1998. – 688 с.
Цыпкин А. Г. Под ред. С. А. Степанова. Справочник по математике для средней школы. – М.: Наука, 1980.- 400 с.
Г. Корн и Т. Корн. Справаочник по математике для начуных работников и инженеров. – М.: Наука, 1970.- 720 с.
[1] ) Под допустимыми понимаются те численные значения букв, при которых выполнимы все операции, совершаемые над буквами, входящими в равенство. Например, допустимыми значениями букв, входящих в равенство

будут следующие; для 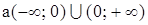 ; для
; для 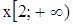 , для
, для 
[2] ) Если a и b имеют разные знаки, то 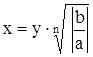 .
.
[3] ) Случай  ,
,  аналогичен разобранному.
аналогичен разобранному.
[4] ) Под алгебраическими преобразованиями уравнения

Понимают следующие преобразования:
1) прибавление к обеим частям уравнения одного и того же алгебраического выражения;
2) умножение обеих частей уравнения на одно и то же алгебраическое выражение;
3) возведение обеих частей уравнения в рациональную степень.



 (21)
(21) , то уравнение (21) приводится к виду
, то уравнение (21) приводится к виду . (22)
. (22) ,
,  . Условию
. Условию  удовлетворяет второй корень квадратного уравнения (22), и число 3 является корнем уравнения (21).
удовлетворяет второй корень квадратного уравнения (22), и число 3 является корнем уравнения (21). , уравнение (21) приводится к виду
, уравнение (21) приводится к виду .
. и
и  . Первый корень
. Первый корень 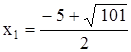 не удовлетворяет условию
не удовлетворяет условию  и поэтому не является решением данного уравнения (21).
и поэтому не является решением данного уравнения (21). .
. . (23)
. (23) ,
,  ,
,  .
. уравнение (23) приводится к виду
уравнение (23) приводится к виду .
. последнее уравнение решений не имеет.
последнее уравнение решений не имеет. уравнение (23) приводится к виду
уравнение (23) приводится к виду
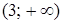 решений не имеет.
решений не имеет. уравнение (23) приводится к виду
уравнение (23) приводится к виду ,
, является решением уравнения (23).
является решением уравнения (23).
 , (24)
, (24) и
и  - некоторые положительные числа
- некоторые положительные числа  . Показательное уравнение (24) эквивалентно алгебраическому уравнению
. Показательное уравнение (24) эквивалентно алгебраическому уравнению .
. , показательное уравнение (24) имеет решение
, показательное уравнение (24) имеет решение
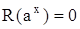 , (25)
, (25) - некоторый многочлен, находится следующим образом.
- некоторый многочлен, находится следующим образом. , и уравнение (25) решается как алгебраическое относительно неизвестного
, и уравнение (25) решается как алгебраическое относительно неизвестного  . После этого решение исходного уравнения (25) сводится к решению простейших показательных уравнений вида (24).
. После этого решение исходного уравнения (25) сводится к решению простейших показательных уравнений вида (24).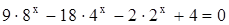 .
.
 , получаем кубическое уравнение относительно переменной
, получаем кубическое уравнение относительно переменной  :
: .
. и два иррациональных корня:
и два иррациональных корня:  и
и  .
. ,
,  ,
, 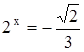 .
. и
и 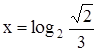 .
.
 сводится к квадратному уравнению
сводится к квадратному уравнению .
.
 сводится к квадратному уравнению
сводится к квадратному уравнению .
.
 сводится к квадратному уравнению
сводится к квадратному уравнению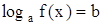 , (26)
, (26) - некоторое положительно число, отличное от единицы,
- некоторое положительно число, отличное от единицы,  - любое действительное число. Логарифмическое уравнение (26) эквивалентно алгебраическому уравнению
- любое действительное число. Логарифмическое уравнение (26) эквивалентно алгебраическому уравнению .
. , логарифмическое уравнение (26) имеет решение
, логарифмическое уравнение (26) имеет решение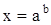 .
. , где
, где  - некоторый многочлен указанного неизвестного, находится следующим образом.
- некоторый многочлен указанного неизвестного, находится следующим образом. , и уравнение (25) решается как алгебраическое уравнение относительно
, и уравнение (25) решается как алгебраическое уравнение относительно  . После этого решаются простейшие логарифмические уравнения вида (25).
. После этого решаются простейшие логарифмические уравнения вида (25).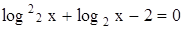 . (27)
. (27) данное уравнение – квадратное:
данное уравнение – квадратное: .
. ,
,  .
. ,
,  ,
, ,
,  .
.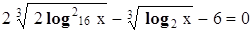 . (28)
. (28) ,
,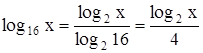 . Подставив в уравнение (28) вместо
. Подставив в уравнение (28) вместо  равную ему величину
равную ему величину  , получаем уравнение
, получаем уравнение .
. это уравнение сводится к квадратному уравнению относительно неизвестного
это уравнение сводится к квадратному уравнению относительно неизвестного  .
. ,
,  . Решаем уравнения
. Решаем уравнения  и
и  :
:

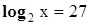
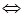
 ,
,


 ,
, .
.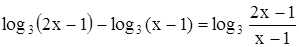 ,
,

 .
.
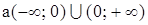 ; для
; для 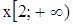 , для
, для 
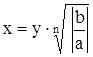 .
. ,
,  аналогичен разобранному.
аналогичен разобранному.


