Гимназия № 12
Сочинение
На тему: Уравнения и способы их решения
Выполнил: ученик 10 "А" класса
Крутько Евгений
Проверила: учитель математики Исхакова Гульсум Акрамовна
Тюмень 2001
Содержание
План................................................................................................................................... 1
Введение........................................................................................................................... 2
Основная часть................................................................................................................. 3
Заключение..................................................................................................................... 25
Приложение................................................................................................................... 26
Список использованной литературы.......................................................................... 29
План.
Введение.
Историческая справка.
Уравнения. Алгебраически уравнения.
а) Основные определения.
б) Линейное уравненение и способ его решения.
в) Квадратные уравнения и способы его решения.
г) Двучленные уравнения способ их решения.
д) Кубические уравнения и способы его решения.
е) Биквадратное уравнение и способ его решения.
ё) Уравнения четвертой степени и способы его решения.
ж) Уравнения высоких степеней и способы из решения.
з) Рациональноное алгебраическое уравнение и способ его
решения.
и) Иррациональные уравнения и способы его решения.
к) Уравнения, содержащие неизвестное под знаком.
абсолютной величины и способ его решения.
Трансцендентные уравнения.
а) Показательные уравнения и способ их решения.
б) Логарифмические уравнения и способ их решения.
Введение
Математическое образование, получаемое в общеобразовательной школе, является важнейшим компонентом общего образования и общей культуры современного человека. Практически все, что окружает современного человека – это все так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Поэтому решение многих практических задач сводится к решению различных видов уравнений, которые необходимо научиться решать.
Данная работа является попыткой обобщить и систематизировать изученный материал по выше указанной теме. Я расположил материал по степени его сложности, начиная с самого простого. В него вошли как известные нам виды уравнений из школьного курс алгебры, так и дополнительный материал. При этом я попытался показать виды уравнений, которые не изучаются в школьном курсе, но знание которых может понадобиться при поступлении в высшее учебное заведение. В своей работе при решении уравнений я не стал ограничиваться только действительным решением, но и указал комплексное, так как считаю, что иначе уравнение просто недорешено. Ведь если в уравнении нет действительных корней, то это еще не значит, что оно не имеет решений. К сожалению, из-за нехватки времени я не смог изложить весь имеющийся у меня материал, но даже по тому материалу, который здесь изложен, может возникнуть множество вопросов. Я надеюсь, что моих знаний хватит для того, чтобы дать ответ на большинство вопросов. Итак, я приступаю к изложению материала.
Математика... выявляет порядок,
симметрию и определенность,
а это – важнейшие виды прекрасного.
Аристотель.
Историческая справка
В те далекие времена, когда мудрецы впервые стали задумываться о равенствах содержащих неизвестные величины, наверное, еще не было ни монет, ни кошельков. Но зато были кучи, а также горшки, корзины, которые прекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. "Ищется куча, которая вместе с двумя третями ее, половиной и одной седьмой составляет 37...", - поучал во II тысячелетии до новой эры египетский писец Ахмес. В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами.
Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Авторы лишь изредка снабжали свои числовые выкладки скупыми комментариями типа: "Смотри!", "Делай так!", "Ты правильно нашел". В этом смысле исключением является "Арифметика" греческого математика Диофанта Александрийского (III в.) – собрание задач на составление уравнений с систематическим изложением их решений.
Однако первым руководством по решению задач, получившим широкую известность, стал труд багдадского ученого IX в. Мухаммеда бен Мусы аль-Хорезми. Слово "аль-джебр" из арабского названия этого трактата – "Китаб аль-джебер валь-мукабала" ("Книга о восстановлении и противопоставлении") – со временем превратилось в хорошо знакомое всем слово "алгебра", а само сочинение аль-Хорезми послужило отправной точкой в становлении науки о решении уравнений.
Линейное уравнение
Линейным уравнением называется уравнение первой степени.
 , (1)
, (1)
где a и b – некоторые действительные числа.
Линейное уравнение всегда имеет единственный корень  , который находится следующим образом.
, который находится следующим образом.
Прибавляя к обеим частям уравнения (1) число  , получаем уравнение
, получаем уравнение
 , (2)
, (2)
эквивалентное уравнению (1). Разделив обе части уравнения (2) на величину  , получаем корень уравнения (1):
, получаем корень уравнения (1):
 .
.
Квадратное уравнение
Алгебраическое уравнение второй степени.
 , (3)
, (3)
где  ,
,  ,
,  – некоторые действительные числа, называется квадратным уравнением. Если
– некоторые действительные числа, называется квадратным уравнением. Если  , то квадратное уравнение (3) называется приведенным.
, то квадратное уравнение (3) называется приведенным.
Корни квадратного уравнения вычисляются по формуле
 ,
,
Выражение  называется дискриминантом квадратного уравнения.
называется дискриминантом квадратного уравнения.
При этом:
если  , то уравнение имеет два различных действительных корня;
, то уравнение имеет два различных действительных корня;
если  , то уравнение имеет один действительный корень кратности 2;
, то уравнение имеет один действительный корень кратности 2;
если  , то уравнение действительных корней не имеет, а имеет два комплексно сопряженных корня:
, то уравнение действительных корней не имеет, а имеет два комплексно сопряженных корня:
 ,
,  ,
,
Частными видами квадратного уравнения (3) являются:
1) Приведенное квадратное уравнение (в случае, если  ), которое обычно записывается в виде
), которое обычно записывается в виде
 .
.
Корни приведенного квадратного уравнения вычисляются по формуле
 . (4)
. (4)
Эту формулу называют формулой Виета – по имени французского математика конца XVI в., внесшего значительный вклад в становление алгебраической символики.
2) Квадратное уравнение с четным вторым коэффициентом, которое обычно записывается в виде
 (
( - целое число).
- целое число).
Корни этого квадратного уравнения удобно вычислять по формуле
 . (5)
. (5)
Формулы (4) и (5) являются частными видами формулы для вычисления корней полного квадратного уравнения.
Корни приведенного квадратного уравнения

связаны с его коэффициентами Формулами Виета
 ,
,
 .
.
В случае, если приведенное квадратное уравнение имеет действительные корни, формулы Виета позволяют судить как о знаках, так и об относительной величине корней квадратного уравнения, а именно:
если  ,
,  , то оба корня отрицательны;
, то оба корня отрицательны;
если  ,
,  , то оба корня положительны;
, то оба корня положительны;
если  ,
,  , то уравнение имеет корни разных знаков, причем отрицательный корень по абсолютной величине больше положительного;
, то уравнение имеет корни разных знаков, причем отрицательный корень по абсолютной величине больше положительного;
если  ,
,  , уравнение имеет корни разных знаков, причем отрицательный корень по абсолютной величине меньше положительного корня.
, уравнение имеет корни разных знаков, причем отрицательный корень по абсолютной величине меньше положительного корня.
Перепишем еще раз квадратное уравнение
 (6)
(6)
и покажем еще один способ как можно вывести корни квадратного уравнения (6) через его коэффициенты и свободный член. Если
 +
+  +
+  , (7)
, (7)
то корни квадратного уравнения вычисляются по формуле
 ,
,
откуда
 ,
,  .
.
которая может быть получена в результате следующих преобразований исходного уравнения, а так же с учетом формулы (7).
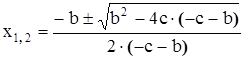

 ,
,
Заметим, что 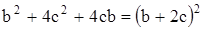 , поэтому
, поэтому


 ,
,
откуда




 .
.


 ,
,
но  , из формулы (7) поэтому окончательно
, из формулы (7) поэтому окончательно
 .
.
Если положить, что 
 +
+  , то
, то


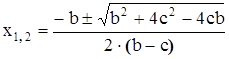 ,
,
Заметим, что  , поэтому
, поэтому


 ,
,
откуда


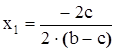 ,
,
но  ,
,  поэтому окончательно
поэтому окончательно
 .
.
и






 .
.
Двучленные уравнения
Уравнения n-й степени вида
 (8)
(8)
называется двучленным уравнением. При 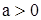 и
и  заменой [2])
заменой [2])
 ,
,
где  - арифметическое значение корня, уравнение (8) приводится к уравнению
- арифметическое значение корня, уравнение (8) приводится к уравнению
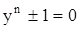 ,
,
которое и будет далее рассматриваться.
Двучленное уравнение  при нечетном n имеет один действительный корень
при нечетном n имеет один действительный корень 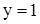 . В множестве комплексных чисел это уравнение имеет n корней (из которых один действительный и
. В множестве комплексных чисел это уравнение имеет n корней (из которых один действительный и  комплексных):
комплексных):
 (
( 0, 1, 2,...,
0, 1, 2,...,  ). (9)
). (9)
Двучленное уравнение  при четном n в множестве действительных чисел имеет два корня
при четном n в множестве действительных чисел имеет два корня 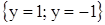 , а в множестве комплексных чисел n корней, вычисляемых по формуле (9).
, а в множестве комплексных чисел n корней, вычисляемых по формуле (9).
Двучленное уравнение  при четном n имеет один действительный корней
при четном n имеет один действительный корней  , а в множестве комплексных чисел
, а в множестве комплексных чисел  корней, вычисляемых по формуле
корней, вычисляемых по формуле
 (
( 0, 1, 2,...,
0, 1, 2,...,  ). (10)
). (10)
Двучленное уравнение  при четном n имеет действительный корней не имеет. В множестве комплексных чисел уравнение имеет
при четном n имеет действительный корней не имеет. В множестве комплексных чисел уравнение имеет  корней, вычисляемых по формуле (10).
корней, вычисляемых по формуле (10).
Приведем краткую сводку множеств корней двучленного уравнения для некоторых конкретных значений n.
1)  (
( ).
).
Уравнение имеет два действительных корня  .
.
2) 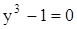 (
(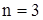 ).
).
Уравнение имеет один дествительный корень  и два комплексных корня
и два комплексных корня
 .
.
3)  (
( ).
).
Уравнение имеет два действительных корния  и два комплексных корня
и два комплексных корня  .
.
4)  (
( ).
).
Уравнение действительных корней не имеет. Комплексные корни:  .
.
5)  (
(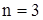 ).
).
Уравнение имеет один дествительный корень 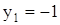 и два комплексных корня
и два комплексных корня
 .
.
6) 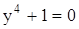 (
( ).
).
Уравнение действительных корней не имеет. Комплексные корни:
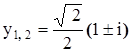 ,
,  .
.
Кубические уравнения
Если квадратные уравнения умели решать еще математики Вавилонии и Древней Индии, то кубические, т.е. уравнения вида
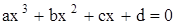 , где
, где  ,
,
оказались "крепким орешком". В конце XV в. профессор математики в университетах Рима и Милана Лука Пачоли в своем знаменитом учебнике "Сумма знаний по арифметике, геометрии, отношениям и пропорциональности" задачу о нахождении общего метода для решения кубических уравнений ставил в один ряд с задачей о квадратуре круга. И все же усилиями итальянских алгебраистов такой метод вскоре был найден.
Начнем с упрощения
Если кубическое уравнение общего вида
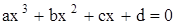 , где
, где  ,
,
разделить на  , то коэффициент при
, то коэффициент при 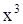 станет равен 1. Поэтому в дальнейшем будем исходить из уравнения
станет равен 1. Поэтому в дальнейшем будем исходить из уравнения
 . (11)
. (11)
Так же как в основе решения квадратного уравнения лежит формула квадрата суммы, решение кубического уравнения опирается на формулу куба суммы:

Чтобы не путаться в коэффициентах, заменим здесь  на
на  и перегруппируем слагаемые:
и перегруппируем слагаемые:
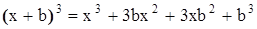 . (12)
. (12)
Мы видим, что надлежащим выбором  , а именно взяв
, а именно взяв  , можно добиться того, что правая часть этой формулы будет отличаться от левой части уравнения (11) только коэффициентом при
, можно добиться того, что правая часть этой формулы будет отличаться от левой части уравнения (11) только коэффициентом при  и свободным членом. Сложим уравнения (11) и (12) и приведем подобные:
и свободным членом. Сложим уравнения (11) и (12) и приведем подобные:
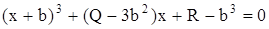 .
.
Если здесь сделать замену  , получим кубическое уравнение относительно
, получим кубическое уравнение относительно  без члена с
без члена с  :
:
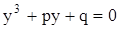 .
.
Итак, мы показали, что в кубическом уравнении (11) с помощью подходящей подстановки можно избавиться от члена, содержащего квадрат неизвестного. Поэтому теперь будем решать уравнение вида
 . (13)
. (13)
Формула Кардано
Давайте еще раз обратимся к формуле куба суммы, но запишем ее иначе:
 .
.
Сравните эту запись с уравнением (13) и попробуйте установить связь между ними. Даже с подсказкой это непросто. Надо отдать должное математикам эпохи Возрождения, решившим кубическое уравнение, не владея буквенной символикой. Подставим в нашу формулу  :
:
 , или
, или
 .
.
Теперь уже ясно: для того, чтобы найти корень уравнения (13), достаточно решить систему уравнений
 или
или 
и взять в качестве  сумму
сумму  и
и  . Заменой
. Заменой  ,
,  эта система приводится к совсем простому виду:
эта система приводится к совсем простому виду:
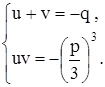
Дальше можно действовать по-разному, но все "дороги" приведут к одному и тому же квадратному уравнению. Например, согласно теореме Виета, сумма корней приведенного квадратного уравнения равна коэффициенту при  со знаком минус, а произведение – свободному члену. Отсюда следует, что
со знаком минус, а произведение – свободному члену. Отсюда следует, что  и
и  - корни уравнения
- корни уравнения
 .
.
Выпишем эти корни:
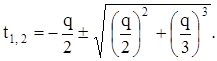
Переменные  и
и  равны кубическим корням из
равны кубическим корням из  и
и  , а искомое решение кубического уравнения (13) – сумма этих корней:
, а искомое решение кубического уравнения (13) – сумма этих корней:
 .
.
Эта формула известная как формула Кардано.
Тригонометрическое решение

подстановкой  приводится к "неполному" виду
приводится к "неполному" виду
 ,
,  ,
,  . (14)
. (14)
Корни  ,
,  ,
,  "неполного" кубичного уравнения (14) равны
"неполного" кубичного уравнения (14) равны
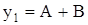 ,
,  ,
,
где
 ,
,  ,
,
 .
.
Пусть "неполное" кубичное уравнение (14) действительно.
а) Если  ("неприводимый" случай), то
("неприводимый" случай), то  и
и
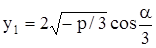 ,
,
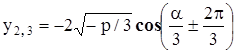 ,
,
где
 .
.
(b) Если  ,
,  , то
, то
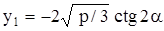 ,
,  ,
,
где

 ,
, 
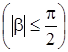 .
.
(с) Если  ,
,  , то
, то
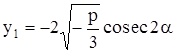 ,
,  ,
,
где

 ,
, 
 .
.
Во всех случаях берется действительное значение кубичного корня.
Биквадратное уравнение
Алгебраическое уравнение четвертой степени.
 ,
,
где a, b, c – некоторые действительные числа, называется биквадратным уравнением. Заменой  уравнение сводится к квадратному уравнению
уравнение сводится к квадратному уравнению  с последующим решением двух двучленных уравнений
с последующим решением двух двучленных уравнений  и
и  (
( и
и  - корни соответствующего квадратного уравнения).
- корни соответствующего квадратного уравнения).
Если  и
и  , то биквадратное уравнение имеет четыре действительных корня:
, то биквадратное уравнение имеет четыре действительных корня:
 ,
,  .
.
Если  ,
,  [3]), то биквадратное уравнение имеет два действительных корня
[3]), то биквадратное уравнение имеет два действительных корня  и мнимых сопряженных корня:
и мнимых сопряженных корня:
 .
.
Если  и
и  , то биквадратное уравнение имеет четыре чисто мнимых попарно сопряженных корня:
, то биквадратное уравнение имеет четыре чисто мнимых попарно сопряженных корня:
 ,
,  .
.
Уравнения четвертой степени
Метод решения уравнений четвертой степени нашел в XVI в. Лудовико Феррари, ученик Джероламо Кардано. Он так и называется – метод Феррари.
Как и при решении кубического и квадратного уравнений, в уравнении четвертой степени

можно избавиться от члена  подстановкой
подстановкой  . Поэтому будем считать, что коэффициент при кубе неизвестного равен нулю:
. Поэтому будем считать, что коэффициент при кубе неизвестного равен нулю:
 .
.
Идея Феррари состояла в том, чтобы представить уравнение в виде  , где левая часть – квадрат выражения
, где левая часть – квадрат выражения  , а правая часть – квадрат линейного уравнения
, а правая часть – квадрат линейного уравнения  от
от  , коэффициенты которого зависят от
, коэффициенты которого зависят от  . После этого останется решить два квадратных уравнения:
. После этого останется решить два квадратных уравнения:  и
и  . Конечно, такое представление возможно только при специальном выборе параметра
. Конечно, такое представление возможно только при специальном выборе параметра  . Удобно взять
. Удобно взять  в виде
в виде  , тогда уравнение перепишется так:
, тогда уравнение перепишется так:
 . (15)
. (15)
Правая часть этого уравнения – квадратный трехчлен от  . Полным квадратом он будет тогда, когда его дискриминант равен нулю, т.е.
. Полным квадратом он будет тогда, когда его дискриминант равен нулю, т.е.
 , или
, или
 .
.
Это уравнение называется резольвентным (т.е. "разрешающим"). Относительно  оно кубическое, и формула Кардано позволяет найти какой-нибудь его корень
оно кубическое, и формула Кардано позволяет найти какой-нибудь его корень  . При
. При  правая часть уравнения (15) принимает вид
правая часть уравнения (15) принимает вид
 ,
,
а само уравнение сводится к двум квадратным:
 .
.
Их корни и дают все решения исходного уравнения.
Решим для примера уравнение
 .
.
Здесь удобнее будет воспользоваться не готовыми формулами, а самой идеей решения. Перепишем уравнение в виде

и добавим к обеим частям выражение  , чтобы в левой части образовался полный квадрат:
, чтобы в левой части образовался полный квадрат:
 .
.
Теперь приравняем к нулю дискриминант правой части уравнения:
 ,
,
или, после упрощения,
 .
.
Один из корней полученного уравнения можно угадать, перебрав делители свободного члена:  . После подстановки этого значения получим уравнение
. После подстановки этого значения получим уравнение
 ,
,
откуда  . Корни образовавшихся квадратных уравнений -
. Корни образовавшихся квадратных уравнений -  и
и  . Разумеется, в общем случае могут получиться и комплексные корни.
. Разумеется, в общем случае могут получиться и комплексные корни.
Решение Декарта-Эйлера

подстановкой  приводится к "неполному" виду
приводится к "неполному" виду
 . (16)
. (16)
Корни  ,
,  ,
,  ,
,  "неполного" уравнения четвертой степени (16) равны одному из выражений
"неполного" уравнения четвертой степени (16) равны одному из выражений


 ,
,
в которых сочетания знаков выбираются так, чтобы удовлетворялось условие


 ,
,
причем  ,
,  и
и  - корни кубичного уравнения
- корни кубичного уравнения
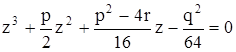 .
.
Уравнения высоких степеней
Разрешимость в радикалах
Формула корней квадратного уравнения известна с незапамятных времен, а в XVI в. итальянские алгебраисты решили в радикалах уравнения третьей и четвертой степеней. Таким образом, было установлено, что корни любого уравнения не выше четвертой степени выражаются через коэффициенты уравнения формулой, в которой используются только четыре арифметические операции (сложение, вычитание, умножение, деление) и извлечение корней степени, не превышающей степень уравнения. Более того, все уравнения данной степени  (
( ) можно "обслужить" одной общей формулой. При подстановке в нее коэффициентов уравнения получим все корни – и действительные, и комплексные.
) можно "обслужить" одной общей формулой. При подстановке в нее коэффициентов уравнения получим все корни – и действительные, и комплексные.
После этого естественно возник вопрос: а есть ли похожие общие формулы для решения уравнений пятой степени и выше? Ответ на него смог найти норвежский математик Нильс Хенрик Абель в начале XIX в. Чуть раньше этот результат был указан, но недостаточно обоснован итальянцем Паоло Руффини. Теорема Абеля-Руффини звучит так:
Общее уравнение степени  при
при  неразрешимо в радикалах.
неразрешимо в радикалах.
Таким образом, общей формулы, применимой ко всем уравнениям данной степени  , не существует. Однако это не значит, что невозможно решить в радикалах те или иные частные виды уравнений высоких степеней. Сам Абель нашел такое решение для широкого класса уравнений произвольно высокой степени – так называемых абелевых уравнений. Теорема Абеля-Руффини не исключает даже и того, что корни каждого конкретного алгебраического уравнения можно записать через его коэффициенты с помощью знаков арифметических операций и радикалов, в частности, что любое алгебраическое число, т.е. корень уравнения вида
, не существует. Однако это не значит, что невозможно решить в радикалах те или иные частные виды уравнений высоких степеней. Сам Абель нашел такое решение для широкого класса уравнений произвольно высокой степени – так называемых абелевых уравнений. Теорема Абеля-Руффини не исключает даже и того, что корни каждого конкретного алгебраического уравнения можно записать через его коэффициенты с помощью знаков арифметических операций и радикалов, в частности, что любое алгебраическое число, т.е. корень уравнения вида
 ,
,  ,
,
с целыми коэффициентами, можно выразить в радикалах через рациональные числа. На самом деле такое выражение существует далеко не всегда. Это следует из теоремы разрешимости алгебраических уравнений, построенной выдающимся французским математиком Эваристом Галуа в его "Мемуаре об условиях разрешимости уравнений в радикалах" (1832 г.; опубликован в 1846 г.).
Подчеркнем, что в прикладных задачах нас интересует только приближенные значения корней уравнения. Поэтому его разрешимость в радикалах здесь обычно роли не играет. Имеются специальные вычислительные методы, позволяющие найти корни любого уравнения с любой наперед заданной точностью, ничуть не меньшей, чем дают вычисления по готовым формулам.
Уравнения, которые решаются
Хотят уравнения высоких степеней в общем случае неразрешимы в радикалах, да и формулы Кардано и Феррари для уравнений третьей и четвертой степеней в школе не проходят, в учебниках по алгебре, на вступительных экзаменах в институты иногда встречаются задачи, где требуется решить уравнения выше второй степени. Обычно их специально подбирают так, чтобы корни уравнений можно было найти с помощью некоторых элементарных приемов.
В основе одного из таких приемов лежит теорема о рациональных корнях многочлена:
Если несократимая дробь 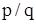 является корнем многочлена
является корнем многочлена  с целыми коэффициентами, то ее числитель
с целыми коэффициентами, то ее числитель  является делителем свободного члена
является делителем свободного члена  , а знаменатель
, а знаменатель  - делителем старшего коэффициента
- делителем старшего коэффициента  .
.
Для доказательства достаточно подставить в уравнение 
 и умножить уравнение на
и умножить уравнение на  . Получим
. Получим
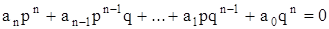 .
.
Все слагаемые в левой части, кроме последнего, делятся на 
|
|
|



 , (1)
, (1) , который находится следующим образом.
, который находится следующим образом. , получаем уравнение
, получаем уравнение , (2)
, (2) , получаем корень уравнения (1):
, получаем корень уравнения (1): .
. , (3)
, (3) ,
,  ,
,  – некоторые действительные числа, называется квадратным уравнением. Если
– некоторые действительные числа, называется квадратным уравнением. Если  , то квадратное уравнение (3) называется приведенным.
, то квадратное уравнение (3) называется приведенным. ,
, называется дискриминантом квадратного уравнения.
называется дискриминантом квадратного уравнения. , то уравнение имеет два различных действительных корня;
, то уравнение имеет два различных действительных корня; , то уравнение имеет один действительный корень кратности 2;
, то уравнение имеет один действительный корень кратности 2; , то уравнение действительных корней не имеет, а имеет два комплексно сопряженных корня:
, то уравнение действительных корней не имеет, а имеет два комплексно сопряженных корня: ,
,  ,
, ), которое обычно записывается в виде
), которое обычно записывается в виде .
. . (4)
. (4) (
( - целое число).
- целое число). . (5)
. (5) ,
, .
. ,
,  , то оба корня отрицательны;
, то оба корня отрицательны; , то оба корня положительны;
, то оба корня положительны; ,
,  ,
,  +
+  , (7)
, (7) ,
, ,
,  .
.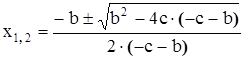

 ,
,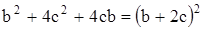 , поэтому
, поэтому
 ,
,

 .
.
 ,
, , из формулы (7) поэтому окончательно
, из формулы (7) поэтому окончательно .
.
 +
+ 
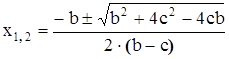 ,
, , поэтому
, поэтому
 ,
,
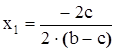 ,
, ,
,  поэтому окончательно
поэтому окончательно .
.


 .
. (8)
(8)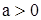 и
и  заменой [2])
заменой [2]) ,
, - арифметическое значение корня, уравнение (8) приводится к уравнению
- арифметическое значение корня, уравнение (8) приводится к уравнению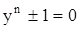 ,
, при нечетном n имеет один действительный корень
при нечетном n имеет один действительный корень 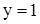 . В множестве комплексных чисел это уравнение имеет n корней (из которых один действительный и
. В множестве комплексных чисел это уравнение имеет n корней (из которых один действительный и  комплексных):
комплексных): (
( 0, 1, 2,...,
0, 1, 2,..., 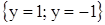 , а в множестве комплексных чисел n корней, вычисляемых по формуле (9).
, а в множестве комплексных чисел n корней, вычисляемых по формуле (9). при четном n имеет один действительный корней
при четном n имеет один действительный корней  , а в множестве комплексных чисел
, а в множестве комплексных чисел  корней, вычисляемых по формуле
корней, вычисляемых по формуле (
( (
( ).
). .
.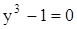 (
(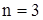 ).
). и два комплексных корня
и два комплексных корня .
. (
( ).
). .
. (
( .
. (
(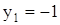 и два комплексных корня
и два комплексных корня .
.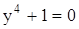 (
(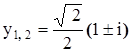 ,
,  .
.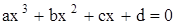 , где
, где  ,
, , то коэффициент при
, то коэффициент при 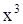 станет равен 1. Поэтому в дальнейшем будем исходить из уравнения
станет равен 1. Поэтому в дальнейшем будем исходить из уравнения . (11)
. (11)
 и перегруппируем слагаемые:
и перегруппируем слагаемые: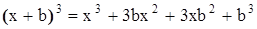 . (12)
. (12) , а именно взяв
, а именно взяв  , можно добиться того, что правая часть этой формулы будет отличаться от левой части уравнения (11) только коэффициентом при
, можно добиться того, что правая часть этой формулы будет отличаться от левой части уравнения (11) только коэффициентом при  и свободным членом. Сложим уравнения (11) и (12) и приведем подобные:
и свободным членом. Сложим уравнения (11) и (12) и приведем подобные: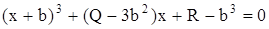 .
. , получим кубическое уравнение относительно
, получим кубическое уравнение относительно  без члена с
без члена с  :
: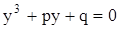 .
. . (13)
. (13) .
. :
: , или
, или .
. или
или 
 сумму
сумму  ,
,  эта система приводится к совсем простому виду:
эта система приводится к совсем простому виду: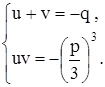
 и
и  - корни уравнения
- корни уравнения .
.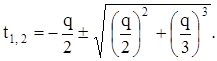
 и
и  и
и  , а искомое решение кубического уравнения (13) – сумма этих корней:
, а искомое решение кубического уравнения (13) – сумма этих корней: .
.
 приводится к "неполному" виду
приводится к "неполному" виду ,
,  ,
,  . (14)
. (14) ,
,  ,
,  "неполного" кубичного уравнения (14) равны
"неполного" кубичного уравнения (14) равны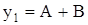 ,
,  ,
, ,
,  ,
, .
. ("неприводимый" случай), то
("неприводимый" случай), то  и
и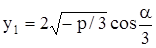 ,
,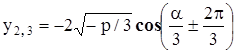 ,
, .
. ,
,  , то
, то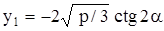 ,
,  ,
,
 ,
, 
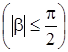 .
. , то
, то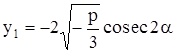 ,
,  ,
,
 .
. ,
, уравнение сводится к квадратному уравнению
уравнение сводится к квадратному уравнению  с последующим решением двух двучленных уравнений
с последующим решением двух двучленных уравнений  и
и  (
( и
и  , то биквадратное уравнение имеет четыре действительных корня:
, то биквадратное уравнение имеет четыре действительных корня: ,
,  .
. [3]), то биквадратное уравнение имеет два действительных корня
[3]), то биквадратное уравнение имеет два действительных корня  и мнимых сопряженных корня:
и мнимых сопряженных корня: .
. и
и  ,
, 
 подстановкой
подстановкой  . Поэтому будем считать, что коэффициент при кубе неизвестного равен нулю:
. Поэтому будем считать, что коэффициент при кубе неизвестного равен нулю: .
. , где левая часть – квадрат выражения
, где левая часть – квадрат выражения  , а правая часть – квадрат линейного уравнения
, а правая часть – квадрат линейного уравнения  от
от  , коэффициенты которого зависят от
, коэффициенты которого зависят от  . После этого останется решить два квадратных уравнения:
. После этого останется решить два квадратных уравнения:  и
и  . Конечно, такое представление возможно только при специальном выборе параметра
. Конечно, такое представление возможно только при специальном выборе параметра  , тогда уравнение перепишется так:
, тогда уравнение перепишется так: . (15)
. (15) . Полным квадратом он будет тогда, когда его дискриминант равен нулю, т.е.
. Полным квадратом он будет тогда, когда его дискриминант равен нулю, т.е. , или
, или .
. оно кубическое, и формула Кардано позволяет найти какой-нибудь его корень
оно кубическое, и формула Кардано позволяет найти какой-нибудь его корень  . При
. При  правая часть уравнения (15) принимает вид
правая часть уравнения (15) принимает вид ,
, .
. .
.
 , чтобы в левой части образовался полный квадрат:
, чтобы в левой части образовался полный квадрат: .
. ,
, .
. . После подстановки этого значения получим уравнение
. После подстановки этого значения получим уравнение ,
, . Корни образовавшихся квадратных уравнений -
. Корни образовавшихся квадратных уравнений -  и
и  . Разумеется, в общем случае могут получиться и комплексные корни.
. Разумеется, в общем случае могут получиться и комплексные корни.
 приводится к "неполному" виду
приводится к "неполному" виду . (16)
. (16) ,
,  ,
,  "неполного" уравнения четвертой степени (16) равны одному из выражений
"неполного" уравнения четвертой степени (16) равны одному из выражений

 ,
,

 ,
, ,
,  и
и  - корни кубичного уравнения
- корни кубичного уравнения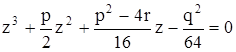 .
. (
( ) можно "обслужить" одной общей формулой. При подстановке в нее коэффициентов уравнения получим все корни – и действительные, и комплексные.
) можно "обслужить" одной общей формулой. При подстановке в нее коэффициентов уравнения получим все корни – и действительные, и комплексные. неразрешимо в радикалах.
неразрешимо в радикалах. , не существует. Однако это не значит, что невозможно решить в радикалах те или иные частные виды уравнений высоких степеней. Сам Абель нашел такое решение для широкого класса уравнений произвольно высокой степени – так называемых абелевых уравнений. Теорема Абеля-Руффини не исключает даже и того, что корни каждого конкретного алгебраического уравнения можно записать через его коэффициенты с помощью знаков арифметических операций и радикалов, в частности, что любое алгебраическое число, т.е. корень уравнения вида
, не существует. Однако это не значит, что невозможно решить в радикалах те или иные частные виды уравнений высоких степеней. Сам Абель нашел такое решение для широкого класса уравнений произвольно высокой степени – так называемых абелевых уравнений. Теорема Абеля-Руффини не исключает даже и того, что корни каждого конкретного алгебраического уравнения можно записать через его коэффициенты с помощью знаков арифметических операций и радикалов, в частности, что любое алгебраическое число, т.е. корень уравнения вида ,
,  ,
,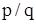 является корнем многочлена
является корнем многочлена  с целыми коэффициентами, то ее числитель
с целыми коэффициентами, то ее числитель  является делителем свободного члена
является делителем свободного члена  , а знаменатель
, а знаменатель  - делителем старшего коэффициента
- делителем старшего коэффициента  .
.
 и умножить уравнение на
и умножить уравнение на  . Получим
. Получим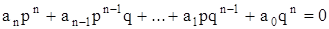 .
.



