

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...

Состав сооружений: решетки и песколовки: Решетки – это первое устройство в схеме очистных сооружений. Они представляют...

Семя – орган полового размножения и расселения растений: наружи у семян имеется плотный покров – кожура...
Топ:
Основы обеспечения единства измерений: Обеспечение единства измерений - деятельность метрологических служб, направленная на достижение...
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Марксистская теория происхождения государства: По мнению Маркса и Энгельса, в основе развития общества, происходящих в нем изменений лежит...
Интересное:
Национальное богатство страны и его составляющие: для оценки элементов национального богатства используются...
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Влияние предпринимательской среды на эффективное функционирование предприятия: Предпринимательская среда – это совокупность внешних и внутренних факторов, оказывающих влияние на функционирование фирмы...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Основные определения
В алгебре рассматриваются два вида равенств – тождества и уравнения.
Тождество – это равенство, которое выполняется при всех (допустимых) значениях входящих в него букв [1]). Для записи тождества наряду со знаком  также используется знак
также используется знак  .
.
Уравнение – это равенство, которое выполняется лишь при некоторых значениях входящих в него букв. Буквы, входящие в уравнение, по условию задачи могут быть неравноправны: одни могут принимать все свои допустимые значения (их называют параметрами или коэффициентами уравнения и обычно обозначают первыми буквами латинского алфавита:  ,
, 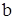 ,
,  ... – или теми же буквами, снабженными индексами:
... – или теми же буквами, снабженными индексами:  ,
,  ,... или
,... или 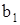 ,
, 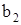 ,...); другие, значения которых требуется отыскать, называют неизвестными (их обычно обозначают последними буквами латинского алфавита:
,...); другие, значения которых требуется отыскать, называют неизвестными (их обычно обозначают последними буквами латинского алфавита:  ,
,  ,
,  ,... – или теми же буквами, снабженными индексами:
,... – или теми же буквами, снабженными индексами:  ,
,  ,... или
,... или  ,
, 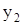 ,...).
,...).
В общем виде уравнение может быть записано так:

 (
( ,
,  ,...,
,...,  )
)  .
.
В зависимости от числа неизвестных уравнение называют уравнением с одним, двумя и т. д. неизвестными.
Значение неизвестных, обращающие уравнение в тождество, называют решениями уравнения.
Решить уравнение – это значит найти множество его решений или доказать, что решений нет. В зависимости от вида уравнения множество решений уравнения может быть бесконечным, конечным и пустым.
Если все решения уравнения 
 являются решениями уравнения
являются решениями уравнения 
 , то говорят, что уравнение
, то говорят, что уравнение 
 есть следствие уравнения
есть следствие уравнения 
 , и пишут
, и пишут


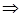

 .
.
Два уравнения

 и
и 

называют эквивалентными, если каждое из них является следствие другого, и пишут




 .
.
Таким образом, два уравнения считаются эквивалентными, если множество решений этих уравнений совпадают.
|
|
Уравнение 
 считают эквивалентным двум (или нескольким) уравнениям
считают эквивалентным двум (или нескольким) уравнениям 
 ,
, 
 , если множество решений уравнения
, если множество решений уравнения 
 совпадает с объединением множеств решений уравнений
совпадает с объединением множеств решений уравнений 
 ,
, 
 .
.
Н е к о т о р ы е э к в и в а л е н т н ы е у р а в н е н и я:
Уравнение  эквивалентно уравнению
эквивалентно уравнению 
 , рассматриваемому на множестве допустимых значений искходного уравнения.
, рассматриваемому на множестве допустимых значений искходного уравнения.
Уравнение  эквивалентно уравнению
эквивалентно уравнению 
 , рассматриваемому на множестве допустимых значений искходного уравнения.
, рассматриваемому на множестве допустимых значений искходного уравнения.
 эквивалентно двум уравнениям
эквивалентно двум уравнениям 
 и
и 
 .
.
Уравнение 
 эквивалентно уравнению
эквивалентно уравнению 
 .
.
Уравнение 

 при нечетном n эквивалентно уравнению
при нечетном n эквивалентно уравнению 
 , а при четном n эквивалентно двум уравнениям
, а при четном n эквивалентно двум уравнениям 
 и
и 
 .
.
Алгебраическим уравнением называется уравнение вида

 ,
,
где  – многочлен n-й степени от одной или нескольких переменных.
– многочлен n-й степени от одной или нескольких переменных.
Алгебраическим уравнением с одним неизвестным называется уравнение, сводящееся к уравнению вида


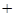
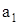
 +
+ 
 +... +
+... + 
 +
+ 
 ,
,
где n – неотрицательное целое число; коэффициенты многочлена  ,
, 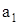 ,
,  ,...,
,...,  ,
,  называются коэффициентами (или параметрами) уравнения и считаются заданными; х называется неизвестным и является искомым. Число n называется степенью уравнения.
называются коэффициентами (или параметрами) уравнения и считаются заданными; х называется неизвестным и является искомым. Число n называется степенью уравнения.
Значения неизвестного х, обращающие алгебраическое уравнение в тождество, называются корнями (реже решениями) алгебраического уравнения.
Есть несколько видов уравнений, которые решаются по готовым формулам. Это линейное и квадратное уравнения, а также уравнения вида F(х)  , где F – одна из стандартных функций (степенная или показательная функция, логарифм, синус, косинус, тангенс или котангенс). Такие уравнения считаются простейшими. Так же существуют формулы и для кубического уравнения, но его к простейшим не относят.
, где F – одна из стандартных функций (степенная или показательная функция, логарифм, синус, косинус, тангенс или котангенс). Такие уравнения считаются простейшими. Так же существуют формулы и для кубического уравнения, но его к простейшим не относят.
Так вот, главная задача при решении любого уравнения – свести его к простейшим.
Все ниже перечисленные уравнения имеют так же и свое графическое решение, которое заключается в том, чтобы представить левую и правую части уравнения как две одинаковые функции от неизвестного. Затем строится график сначала одной функции, а затем другой и точка(и) пересечения двух графиков даст решение(я) исходного уравнения. Примеры графического решения всех уравнений даны в приложении.
|
|
Линейное уравнение
Линейным уравнением называется уравнение первой степени.
 , (1)
, (1)
где a и b – некоторые действительные числа.
Линейное уравнение всегда имеет единственный корень  , который находится следующим образом.
, который находится следующим образом.
Прибавляя к обеим частям уравнения (1) число  , получаем уравнение
, получаем уравнение
 , (2)
, (2)
эквивалентное уравнению (1). Разделив обе части уравнения (2) на величину  , получаем корень уравнения (1):
, получаем корень уравнения (1):
 .
.
Квадратное уравнение
Алгебраическое уравнение второй степени.
 , (3)
, (3)
где  ,
,  ,
,  – некоторые действительные числа, называется квадратным уравнением. Если
– некоторые действительные числа, называется квадратным уравнением. Если  , то квадратное уравнение (3) называется приведенным.
, то квадратное уравнение (3) называется приведенным.
Корни квадратного уравнения вычисляются по формуле
 ,
,
Выражение  называется дискриминантом квадратного уравнения.
называется дискриминантом квадратного уравнения.
При этом:
если  , то уравнение имеет два различных действительных корня;
, то уравнение имеет два различных действительных корня;
если  , то уравнение имеет один действительный корень кратности 2;
, то уравнение имеет один действительный корень кратности 2;
если  , то уравнение действительных корней не имеет, а имеет два комплексно сопряженных корня:
, то уравнение действительных корней не имеет, а имеет два комплексно сопряженных корня:
 ,
,  ,
,
Частными видами квадратного уравнения (3) являются:
1) Приведенное квадратное уравнение (в случае, если  ), которое обычно записывается в виде
), которое обычно записывается в виде
 .
.
Корни приведенного квадратного уравнения вычисляются по формуле
 . (4)
. (4)
Эту формулу называют формулой Виета – по имени французского математика конца XVI в., внесшего значительный вклад в становление алгебраической символики.
2) Квадратное уравнение с четным вторым коэффициентом, которое обычно записывается в виде
 (
( - целое число).
- целое число).
Корни этого квадратного уравнения удобно вычислять по формуле
 . (5)
. (5)
|
|
Формулы (4) и (5) являются частными видами формулы для вычисления корней полного квадратного уравнения.
Корни приведенного квадратного уравнения

связаны с его коэффициентами Формулами Виета
 ,
,
 .
.
В случае, если приведенное квадратное уравнение имеет действительные корни, формулы Виета позволяют судить как о знаках, так и об относительной величине корней квадратного уравнения, а именно:
если  ,
,  , то оба корня отрицательны;
, то оба корня отрицательны;
если  ,
,  , то оба корня положительны;
, то оба корня положительны;
если  ,
,  , то уравнение имеет корни разных знаков, причем отрицательный корень по абсолютной величине больше положительного;
, то уравнение имеет корни разных знаков, причем отрицательный корень по абсолютной величине больше положительного;
если  ,
,  , уравнение имеет корни разных знаков, причем отрицательный корень по абсолютной величине меньше положительного корня.
, уравнение имеет корни разных знаков, причем отрицательный корень по абсолютной величине меньше положительного корня.
Перепишем еще раз квадратное уравнение
 (6)
(6)
и покажем еще один способ как можно вывести корни квадратного уравнения (6) через его коэффициенты и свободный член. Если
 +
+  +
+  , (7)
, (7)
то корни квадратного уравнения вычисляются по формуле
 ,
,
откуда
 ,
,  .
.
которая может быть получена в результате следующих преобразований исходного уравнения, а так же с учетом формулы (7).
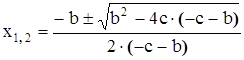

 ,
,
Заметим, что 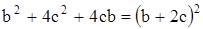 , поэтому
, поэтому


 ,
,
откуда




 .
.


 ,
,
но 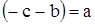 , из формулы (7) поэтому окончательно
, из формулы (7) поэтому окончательно
 .
.
Если положить, что 
 +
+  , то
, то


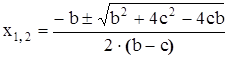 ,
,
Заметим, что  , поэтому
, поэтому


 ,
,
откуда


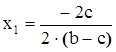 ,
,
но  ,
,  поэтому окончательно
поэтому окончательно
 .
.
и






 .
.
Двучленные уравнения
Уравнения n-й степени вида
 (8)
(8)
называется двучленным уравнением. При 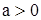 и
и  заменой [2])
заменой [2])
 ,
,
где  - арифметическое значение корня, уравнение (8) приводится к уравнению
- арифметическое значение корня, уравнение (8) приводится к уравнению
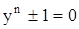 ,
,
которое и будет далее рассматриваться.
Двучленное уравнение  при нечетном n имеет один действительный корень
при нечетном n имеет один действительный корень 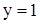 . В множестве комплексных чисел это уравнение имеет n корней (из которых один действительный и
. В множестве комплексных чисел это уравнение имеет n корней (из которых один действительный и  комплексных):
комплексных):
|
|
 (
( 0, 1, 2,...,
0, 1, 2,...,  ). (9)
). (9)
Двучленное уравнение  при четном n в множестве действительных чисел имеет два корня
при четном n в множестве действительных чисел имеет два корня 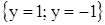 , а в множестве комплексных чисел n корней, вычисляемых по формуле (9).
, а в множестве комплексных чисел n корней, вычисляемых по формуле (9).
Двучленное уравнение  при четном n имеет один действительный корней
при четном n имеет один действительный корней  , а в множестве комплексных чисел
, а в множестве комплексных чисел  корней, вычисляемых по формуле
корней, вычисляемых по формуле
 (
( 0, 1, 2,...,
0, 1, 2,...,  ). (10)
). (10)
Двучленное уравнение  при четном n имеет действительный корней не имеет. В множестве комплексных чисел уравнение имеет
при четном n имеет действительный корней не имеет. В множестве комплексных чисел уравнение имеет  корней, вычисляемых по формуле (10).
корней, вычисляемых по формуле (10).
Приведем краткую сводку множеств корней двучленного уравнения для некоторых конкретных значений n.
1)  (
( ).
).
Уравнение имеет два действительных корня  .
.
2) 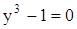 (
(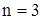 ).
).
Уравнение имеет один дествительный корень  и два комплексных корня
и два комплексных корня
 .
.
3)  (
( ).
).
Уравнение имеет два действительных корния  и два комплексных корня
и два комплексных корня  .
.
4)  (
( ).
).
Уравнение действительных корней не имеет. Комплексные корни:  .
.
5)  (
(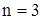 ).
).
Уравнение имеет один дествительный корень 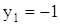 и два комплексных корня
и два комплексных корня
 .
.
6) 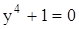 (
( ).
).
Уравнение действительных корней не имеет. Комплексные корни:
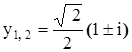 ,
,  .
.
Кубические уравнения
Если квадратные уравнения умели решать еще математики Вавилонии и Древней Индии, то кубические, т.е. уравнения вида
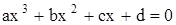 , где
, где  ,
,
оказались "крепким орешком". В конце XV в. профессор математики в университетах Рима и Милана Лука Пачоли в своем знаменитом учебнике "Сумма знаний по арифметике, геометрии, отношениям и пропорциональности" задачу о нахождении общего метода для решения кубических уравнений ставил в один ряд с задачей о квадратуре круга. И все же усилиями итальянских алгебраистов такой метод вскоре был найден.
Начнем с упрощения
Если кубическое уравнение общего вида
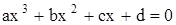 , где
, где  ,
,
разделить на  , то коэффициент при
, то коэффициент при 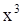 станет равен 1. Поэтому в дальнейшем будем исходить из уравнения
станет равен 1. Поэтому в дальнейшем будем исходить из уравнения
 . (11)
. (11)
Так же как в основе решения квадратного уравнения лежит формула квадрата суммы, решение кубического уравнения опирается на формулу куба суммы:

Чтобы не путаться в коэффициентах, заменим здесь  на
на  и перегруппируем слагаемые:
и перегруппируем слагаемые:
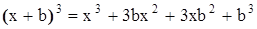 . (12)
. (12)
Мы видим, что надлежащим выбором  , а именно взяв
, а именно взяв  , можно добиться того, что правая часть этой формулы будет отличаться от левой части уравнения (11) только коэффициентом при
, можно добиться того, что правая часть этой формулы будет отличаться от левой части уравнения (11) только коэффициентом при  и свободным членом. Сложим уравнения (11) и (12) и приведем подобные:
и свободным членом. Сложим уравнения (11) и (12) и приведем подобные:
|
|
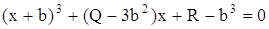 .
.
Если здесь сделать замену  , получим кубическое уравнение относительно
, получим кубическое уравнение относительно  без члена с
без члена с  :
:
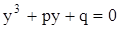 .
.
Итак, мы показали, что в кубическом уравнении (11) с помощью подходящей подстановки можно избавиться от члена, содержащего квадрат неизвестного. Поэтому теперь будем решать уравнение вида
 . (13)
. (13)
Формула Кардано
Давайте еще раз обратимся к формуле куба суммы, но запишем ее иначе:
 .
.
Сравните эту запись с уравнением (13) и попробуйте установить связь между ними. Даже с подсказкой это непросто. Надо отдать должное математикам эпохи Возрождения, решившим кубическое уравнение, не владея буквенной символикой. Подставим в нашу формулу  :
:
 , или
, или
 .
.
Теперь уже ясно: для того, чтобы найти корень уравнения (13), достаточно решить систему уравнений
 или
или 
и взять в качестве  сумму
сумму  и
и  . Заменой
. Заменой  ,
,  эта система приводится к совсем простому виду:
эта система приводится к совсем простому виду:
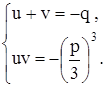
Дальше можно действовать по-разному, но все "дороги" приведут к одному и тому же квадратному уравнению. Например, согласно теореме Виета, сумма корней приведенного квадратного уравнения равна коэффициенту при  со знаком минус, а произведение – свободному члену. Отсюда следует, что
со знаком минус, а произведение – свободному члену. Отсюда следует, что  и
и  - корни уравнения
- корни уравнения
 .
.
Выпишем эти корни:
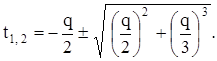
Переменные  и
и  равны кубическим корням из
равны кубическим корням из  и
и  , а искомое решение кубического уравнения (13) – сумма этих корней:
, а искомое решение кубического уравнения (13) – сумма этих корней:
 .
.
Эта формула известная как формула Кардано.
Тригонометрическое решение

подстановкой  приводится к "неполному" виду
приводится к "неполному" виду
 ,
,  ,
,  . (14)
. (14)
Корни  ,
,  ,
,  "неполного" кубичного уравнения (14) равны
"неполного" кубичного уравнения (14) равны
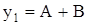 ,
,  ,
,
где
 ,
,  ,
,
 .
.
Пусть "неполное" кубичное уравнение (14) действительно.
а) Если  ("неприводимый" случай), то
("неприводимый" случай), то  и
и
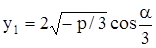 ,
,
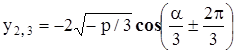 ,
,
где
 .
.
(b) Если  ,
,  , то
, то
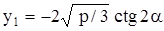 ,
,  ,
,
где

 ,
, 
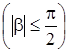 .
.
(с) Если  ,
,  , то
, то
 ,
,  ,
,
где

 ,
, 
 .
.
Во всех случаях берется действительное значение кубичного корня.
Биквадратное уравнение
Алгебраическое уравнение четвертой степени.
 ,
,
где a, b, c – некоторые действительные числа, называется биквадратным уравнением. Заменой  уравнение сводится к квадратному уравнению
уравнение сводится к квадратному уравнению  с последующим решением двух двучленных уравнений
с последующим решением двух двучленных уравнений  и
и  (
( и
и  - корни соответствующего квадратного уравнения).
- корни соответствующего квадратного уравнения).
Если  и
и  , то биквадратное уравнение имеет четыре действительных корня:
, то биквадратное уравнение имеет четыре действительных корня:
 ,
,  .
.
Если  ,
,  [3]), то биквадратное уравнение имеет два действительных корня
[3]), то биквадратное уравнение имеет два действительных корня  и мнимых сопряженных корня:
и мнимых сопряженных корня:
 .
.
Если  и
и  , то биквадратное уравнение имеет четыре чисто мнимых попарно сопряженных корня:
, то биквадратное уравнение имеет четыре чисто мнимых попарно сопряженных корня:
 ,
,  .
.
Уравнения четвертой степени
Метод решения уравнений четвертой степени нашел в XVI в. Лудовико Феррари, ученик Джероламо Кардано. Он так и называется – метод Феррари.
Как и при решении кубического и квадратного уравнений, в уравнении четвертой степени

можно избавиться от члена  подстановкой
подстановкой  . Поэтому будем считать, что коэффициент при кубе неизвестного равен нулю:
. Поэтому будем считать, что коэффициент при кубе неизвестного равен нулю:
 .
.
Идея Феррари состояла в том, чтобы представить уравнение в виде  , где левая часть – квадрат выражения
, где левая часть – квадрат выражения  , а правая часть – квадрат линейного уравнения
, а правая часть – квадрат линейного уравнения  от
от  , коэффициенты которого зависят от
, коэффициенты которого зависят от  . После этого останется решить два квадратных уравнения:
. После этого останется решить два квадратных уравнения:  и
и  . Конечно, такое представление возможно только при специальном выборе параметра
. Конечно, такое представление возможно только при специальном выборе параметра  . Удобно взять
. Удобно взять  в виде
в виде  , тогда уравнение перепишется так:
, тогда уравнение перепишется так:
 . (15)
. (15)
Правая часть этого уравнения – квадратный трехчлен от  . Полным квадратом он будет тогда, когда его дискриминант равен нулю, т.е.
. Полным квадратом он будет тогда, когда его дискриминант равен нулю, т.е.
 , или
, или
 .
.
Это уравнение называется резольвентным (т.е. "разрешающим"). Относительно  оно кубическое, и формула Кардано позволяет найти какой-нибудь его корень
оно кубическое, и формула Кардано позволяет найти какой-нибудь его корень  . При
. При  правая часть уравнения (15) принимает вид
правая часть уравнения (15) принимает вид
 ,
,
а само уравнение сводится к двум квадратным:
 .
.
Их корни и дают все решения исходного уравнения.
Решим для примера уравнение
 .
.
Здесь удобнее будет воспользоваться не готовыми формулами, а самой идеей решения. Перепишем уравнение в виде

и добавим к обеим частям выражение  , чтобы в левой части образовался полный квадрат:
, чтобы в левой части образовался полный квадрат:
 .
.
Теперь приравняем к нулю дискриминант правой части уравнения:
 ,
,
или, после упрощения,
 .
.
Один из корней полученного уравнения можно угадать, перебрав делители свободного члена:  . После подстановки этого значения получим уравнение
. После подстановки этого значения получим уравнение
 ,
,
откуда  . Корни образовавшихся квадратных уравнений -
. Корни образовавшихся квадратных уравнений -  и
и  . Разумеется, в общем случае могут получиться и комплексные корни.
. Разумеется, в общем случае могут получиться и комплексные корни.
Решение Декарта-Эйлера

подстановкой  приводится к "неполному" виду
приводится к "неполному" виду
 . (16)
. (16)
Корни  ,
,  ,
,  ,
,  "неполного" уравнения четвертой степени (16) равны одному из выражений
"неполного" уравнения четвертой степени (16) равны одному из выражений


 ,
,
в которых сочетания знаков выбираются так, чтобы удовлетворялось условие


 ,
,
причем  ,
,  и
и  - корни кубичного уравнения
- корни кубичного уравнения
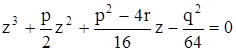 .
.
Уравнения высоких степеней
Разрешимость в радикалах
Формула корней квадратного уравнения известна с незапамятных времен, а в XVI в. итальянские алгебраисты решили в радикалах уравнения третьей и четвертой степеней. Таким образом, было установлено, что корни любого уравнения не выше четвертой степени выражаются через коэффициенты уравнения формулой, в которой используются только четыре арифметические операции (сложение, вычитание, умножение, деление) и извлечение корней степени, не превышающей степень уравнения. Более того, все уравнения данной степени  (
( ) можно "обслужить" одной общей формулой. При подстановке в нее коэффициентов уравнения получим все корни – и действительные, и комплексные.
) можно "обслужить" одной общей формулой. При подстановке в нее коэффициентов уравнения получим все корни – и действительные, и комплексные.
После этого естественно возник вопрос: а есть ли похожие общие формулы для решения уравнений пятой степени и выше? Ответ на него смог найти норвежский математик Нильс Хенрик Абель в начале XIX в. Чуть раньше этот результат был указан, но недостаточно обоснован итальянцем Паоло Руффини. Теорема Абеля-Руффини звучит так:
Общее уравнение степени  при
при  неразрешимо в радикалах.
неразрешимо в радикалах.
Таким образом, общей формулы, применимой ко всем уравнениям данной степени  , не существует. Однако это не значит, что невозможно решить в радикалах те или иные частные виды уравнений высоких степеней. Сам Абель нашел такое решение для широкого класса уравнений произвольно высокой <
, не существует. Однако это не значит, что невозможно решить в радикалах те или иные частные виды уравнений высоких степеней. Сам Абель нашел такое решение для широкого класса уравнений произвольно высокой <
|
|
|

Папиллярные узоры пальцев рук - маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни...
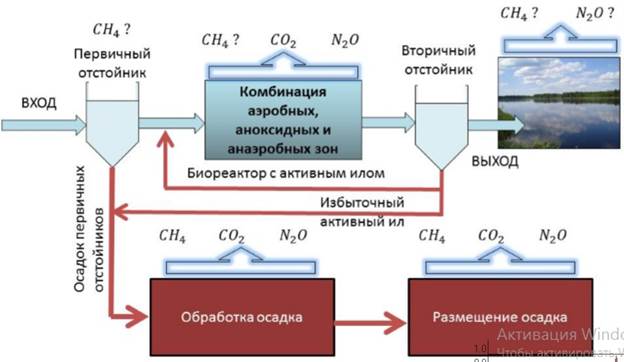
Эмиссия газов от очистных сооружений канализации: В последние годы внимание мирового сообщества сосредоточено на экологических проблемах...

Архитектура электронного правительства: Единая архитектура – это методологический подход при создании системы управления государства, который строится...

Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!