Если каждому возможному значению случайной величины Х соответствует одно возможное значение случайной величины Y, то Y называют функцией случайного аргумента:  .
.
Если Х – дискретная случайная величина, а функция  - монотонна, то различным значениям Х соответствует различные значения Y, а вероятности соответствующих значений Х и Y равны:
- монотонна, то различным значениям Х соответствует различные значения Y, а вероятности соответствующих значений Х и Y равны:

Если  - немонотонная функция, то различным значениям Х могут соответствовать одинаковые значения Y, для которых вероятности находятся, как суммы вероятностей соответствующих значений Х:
- немонотонная функция, то различным значениям Х могут соответствовать одинаковые значения Y, для которых вероятности находятся, как суммы вероятностей соответствующих значений Х:
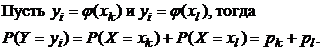
Если Х – непрерывная случайная величина с плотностью распределения f (x), а функция 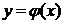 - дифференцируемая монотонная функция, то для отыскания плотности распределения g (y) случайной величины Y находят:
- дифференцируемая монотонная функция, то для отыскания плотности распределения g (y) случайной величины Y находят:
1. функцию  , обратную функции
, обратную функции 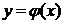 ;
;
2. функцию  ;
;
3. производную  .
.
Тогда плотность распределения g (y) случайной величины Y будет равна:
 . (37)
. (37)
Если каждой паре возможных значений случайных величин Х и Y соответствует одно возможное значение случайной величины Z, то Z называют функцией двух случайных аргументов Х и Y:  , [4, c. 207].
, [4, c. 207].
Пусть Z = Х + Y. Тогда для отыскания значений Z находят всевозможные суммы значений Х и Y (в случае произведения Х и Y – всевозможные произведения значений, в случае разности – всевозможные разности). Если Х и Y независимы, то вероятности значений Z (в любом из указанных случаев) находят как произведения вероятностей соответствующих значений Х и Y. Таким образом, если zi = xj + yk, то p (zi) = p (xj)∙ p (yk) (аналогично, если zi = xj ∙ yk или zi = xj – yk).
Закон распределения двумерной дискретной случайной величины можно так же, как и при распределении одномерной дискретной случайной величины, задать аналитически и с помощью таблицы.
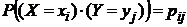 (20)
(20)
Таблица 5 – Закон распределения двумерной дискретной случайной величины (Х, Y)
| уj
xi
| у 1
| у 2
| …
| уj
| …
| уm
| Вероятности значений Х
|
| x 1
| p 11
| p 12
| …
| p 1 j
| …
| p1m
| 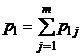
|
| x 2
| p 21
| p 22
| …
| p 2 j
| …
| p2m
| 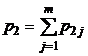
|
| …
| …
| …
| …
| …
| …
| …
|
|
| xi
| pi 1
| pi 2
| …
| pij
| …
| pim
| 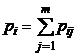
|
| …
| …
| …
| …
| …
| …
| …
|
|
| xn
| pn 1
| pn 2
| …
| pnj
| …
| pnm
| 
|
| Вероятности значений Y
| 
| 
|
| 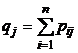
|
| 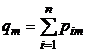
| 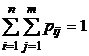
|
В последнем столбце таблицы 5 указаны вероятности значений случайной величины X, а в последней строке – вероятности значений случайной величины Y. Найденные значения вероятностей каждой из случайных величин позволят составить соответствующие этим величинам законы распределения, [5, c. 124].
В случае отыскания условных законов распределения можно воспользоваться формулой (39), подставляя в неё соответствующие определённым условиям значения вероятностей. В формуле (39) приведены вероятности событий  . Каждое из них заключается в том, что величина X принимает некоторое конкретное значение
. Каждое из них заключается в том, что величина X принимает некоторое конкретное значение 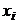 при условии, что Y принимает заранее определённое значение
при условии, что Y принимает заранее определённое значение 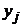 .
.
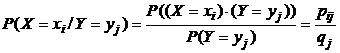 . (21)
. (21)
Используя формулу (21) получим условный закон распределения величины X при условии, что Y принимает значение 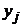 (табл. 6). При этом
(табл. 6). При этом 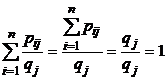 .
.
Таблица 6 – Условный закон распределения случайной величины Х
Функция распределения двумерной дискретной случайной величины определяется по формуле: 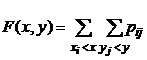 . Её свойства аналогичны свойствам функции распределения одномерной случайной величины и вытекают из них.
. Её свойства аналогичны свойствам функции распределения одномерной случайной величины и вытекают из них.
Функция распределения двумерной непрерывной случайной величины может быть найдена через её плотность распределения по формуле (40).
Плотность распределения двумерной непрерывной случайной величины f (x, y) имеет свойства, вытекающие из свойств функции распределения одномерной случайной величины. Для f (x, y) выполняется:
1. 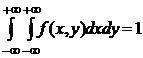 .
.
2. 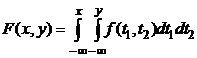
3. 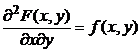 .
.
4. Вероятность попадания случайной точки (x, y), каждая координата которой принадлежит множеству действительных чисел R, в область  равна
равна  .
.
5. Плотности распределения  и
и 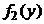 случайных величин соответственно Х и Y двумерной случайной величины (Х, Y) можно получить, зная плотность распределения f (x, y):
случайных величин соответственно Х и Y двумерной случайной величины (Х, Y) можно получить, зная плотность распределения f (x, y):
 ;
; 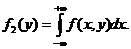
ПРИМЕРЫ ЗАДАЧ С РЕШЕНИЯМИ
2.1 Задачи на основные понятия и теоремы теории вероятностей
 Задача 2.1.1
Задача 2.1.1
Покупатель приобрёл телевизор и магнитофон. Вероятность того, что в течение гарантийного срока не выйдет из строя телевизор, равна 0,85, а для магнитофона она равна 0,98. Найти вероятность того, что
а) оба они выдержат гарантийный срок службы;
б) хотя бы один из них не выдержит гарантийного срока службы.
Решение:
Рассмотрим события:
А - в течение гарантийного срока не выйдет из строя телевизор,
В - в течение гарантийного срока не выйдет из строя магнитофон.
По условию задачи
Р (А) = 0,85; Р (В) = 0,98.
а) Пусть событие С заключается в том, что оба они выдержат гарантийный срок службы, тогда С = А · В.
Так как события А и В независимы, то по теореме (13) умножения вероятностей Р (С) = Р (А)· Р (В). То есть Р (С) = 0,85· 0,98 = 0,833 ≈ 83 %.
б) Пусть событие D заключается в том, что хотя бы одно изделие не выдержит гарантийного срока службы. Тогда событие 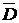 означает, что оба изделия будут исправны:
означает, что оба изделия будут исправны:
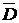 = С = А · В, Р (
= С = А · В, Р (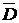 ) = 0,833. Найдём P (D):
) = 0,833. Найдём P (D):
P (D) = 1 – P (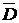 ) = 1 - 0,833 = 0,167 ≈ 17 %.
) = 1 - 0,833 = 0,167 ≈ 17 %.
Ответ: а) вероятность того, что оба изделия выдержат гарантийный срок службы, равна 83 %; б) вероятность того, что хотя бы одно из них не выдержит гарантийного срока службы, равна 17%.
Задача 2.1.2
Предполагая, что для шахматиста в каждой партии равновероятны три исхода: выигрыш, ничья и проигрыш, найти вероятность того, что из четырёх партий шахматист
а) не проиграет ни одной партии;
б) проиграет хотя бы две партии.
Решение:
а) Рассмотрим события: Н 1 – выигрыш, Н 2 – ничья, Н 3 – проигрыш, В – шахматист не проиграет ни одной партии; Вi – шахматист не проиграет i - ую партию, i = 1, 2, 3, 4.
При этом, Вi = Н 2 + Н 3, а В = В 1 · В 2 · В 3 · В 4. Так как события Вi независимы, то согласно формуле (13), Р (В) = Р (В 1)· Р (В 2)· Р (В 3)· Р (В 4).
Найдём вероятности событий Вi:
По условию задачи Р (Н 1)= Р (Н 2)= Р (Н 3), а так как эти события образуют полную группу в случае одной партии, то вероятность каждого из них р =  . Тогда, согласно формуле (10), так как события Н 2 и Н 3 несовместны, Р (Вi)=
. Тогда, согласно формуле (10), так как события Н 2 и Н 3 несовместны, Р (Вi)=  +
+  =
=  . Следовательно,
. Следовательно, 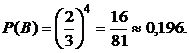
 б) Пусть события Сi означают проигрыш i партий, i = 0, 1, 2, 3, 4. Тогда событие С – проиграть хотя бы две партии – можно выразить следующим образом:
б) Пусть события Сi означают проигрыш i партий, i = 0, 1, 2, 3, 4. Тогда событие С – проиграть хотя бы две партии – можно выразить следующим образом:
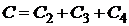 .
.
Событием, противоположным С, будет событие  , при этом
, при этом 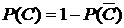 . Найдём вероятность
. Найдём вероятность 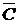 . Так как события
. Так как события  несовместны, по теореме сложения вероятностей (10) получим:
несовместны, по теореме сложения вероятностей (10) получим:
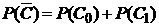 . При этом
. При этом
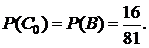
Так как 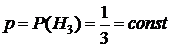 для каждой парии, а все партии – независимые испытания, то для отыскания
для каждой парии, а все партии – независимые испытания, то для отыскания 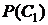 можно использовать формулу Бернулли (16):
можно использовать формулу Бернулли (16):
 .
.
Тогда

а 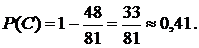
Ответ: а) вероятность того, что из четырёх партий шахматист не проиграет ни одной партии, равна 20%; б) вероятность того, что из четырёх партий шахматист проиграет хотя бы две партии, равна 41%.
Задача 2.1.3 (о встрече)
Двое приятелей договорились встретиться с 10 до 11 часов в определенном месте, причём пришедший первым ждет в течение 20 минут, после чего уходит. Найти вероятность встречи.
Решение:
 Пусть событие А соответствует встрече. Если за х обозначить время прихода первого товарища, а за у – второго, то условие их встречи можно задать системой неравенств:
Пусть событие А соответствует встрече. Если за х обозначить время прихода первого товарища, а за у – второго, то условие их встречи можно задать системой неравенств:
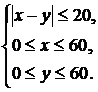
На плоскости хОу область 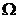 , соответствующая общему числу исходов, будет определена системой
, соответствующая общему числу исходов, будет определена системой  , а область D, соответствующая числу исходов, благоприятствующих событию А, определяется неравенством
, а область D, соответствующая числу исходов, благоприятствующих событию А, определяется неравенством 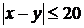 (рисунок 1).
(рисунок 1).
Из последнего неравенства получим:
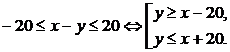
Тогда по определению геометрической вероятности (8), вероятность события А будет равна:
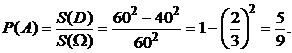
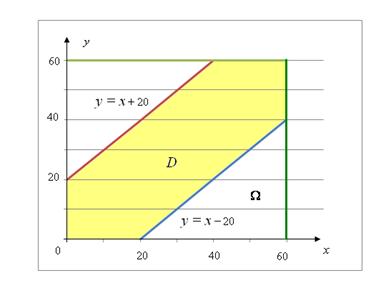
Рисунок 1 – Области для отыскания геометрической
вероятности в задаче 2.1.3
Ответ: вероятность встречи равна 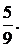
Задача 2.1.4
Доказать, что для событий А и В выполняется: 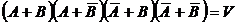 , где
, где  - невозможное событие.
- невозможное событие.
Решение:
По свойствам действий над событиями (стр. 9) получим:




 .
.
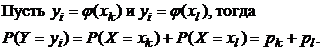
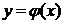 - дифференцируемая монотонная функция, то для отыскания плотности распределения g (y) случайной величины Y находят:
- дифференцируемая монотонная функция, то для отыскания плотности распределения g (y) случайной величины Y находят: , обратную функции
, обратную функции  ;
; .
. . (37)
. (37) , [4, c. 207].
, [4, c. 207].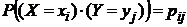 (20)
(20)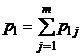
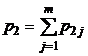
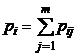



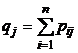
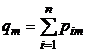
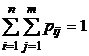
 . Каждое из них заключается в том, что величина X принимает некоторое конкретное значение
. Каждое из них заключается в том, что величина X принимает некоторое конкретное значение 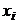 при условии, что Y принимает заранее определённое значение
при условии, что Y принимает заранее определённое значение 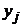 .
.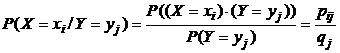 . (21)
. (21)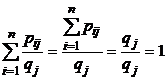 .
.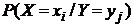

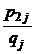

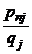
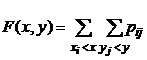 . Её свойства аналогичны свойствам функции распределения одномерной случайной величины и вытекают из них.
. Её свойства аналогичны свойствам функции распределения одномерной случайной величины и вытекают из них.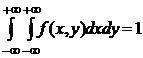 .
.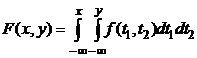
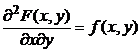 .
. равна
равна  .
. и
и 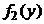 случайных величин соответственно Х и Y двумерной случайной величины (Х, Y) можно получить, зная плотность распределения f (x, y):
случайных величин соответственно Х и Y двумерной случайной величины (Х, Y) можно получить, зная плотность распределения f (x, y): ;
; 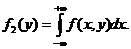
 Задача 2.1.1
Задача 2.1.1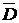 означает, что оба изделия будут исправны:
означает, что оба изделия будут исправны: . Тогда, согласно формуле (10), так как события Н 2 и Н 3 несовместны, Р (Вi)=
. Тогда, согласно формуле (10), так как события Н 2 и Н 3 несовместны, Р (Вi)=  . Следовательно,
. Следовательно, 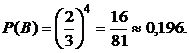
 б) Пусть события Сi означают проигрыш i партий, i = 0, 1, 2, 3, 4. Тогда событие С – проиграть хотя бы две партии – можно выразить следующим образом:
б) Пусть события Сi означают проигрыш i партий, i = 0, 1, 2, 3, 4. Тогда событие С – проиграть хотя бы две партии – можно выразить следующим образом: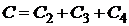 .
. , при этом
, при этом 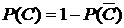 . Найдём вероятность
. Найдём вероятность 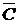 . Так как события
. Так как события  несовместны, по теореме сложения вероятностей (10) получим:
несовместны, по теореме сложения вероятностей (10) получим: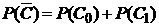 . При этом
. При этом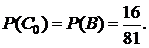
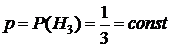 для каждой парии, а все партии – независимые испытания, то для отыскания
для каждой парии, а все партии – независимые испытания, то для отыскания 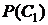 можно использовать формулу Бернулли (16):
можно использовать формулу Бернулли (16): .
.
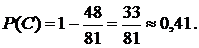
 Пусть событие А соответствует встрече. Если за х обозначить время прихода первого товарища, а за у – второго, то условие их встречи можно задать системой неравенств:
Пусть событие А соответствует встрече. Если за х обозначить время прихода первого товарища, а за у – второго, то условие их встречи можно задать системой неравенств: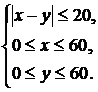
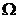 , соответствующая общему числу исходов, будет определена системой
, соответствующая общему числу исходов, будет определена системой  , а область D, соответствующая числу исходов, благоприятствующих событию А, определяется неравенством
, а область D, соответствующая числу исходов, благоприятствующих событию А, определяется неравенством 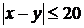 (рисунок 1).
(рисунок 1).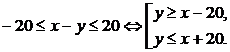
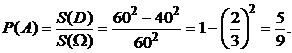

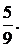
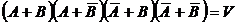 , где
, где  - невозможное событие.
- невозможное событие.


