Для определения устойчивости можно воспользоваться известными в линейной теории критериями устойчивости, применив их к импульсным системам. Рассмотрим структурную схему импульсной системы (рис. 25).

Рис. 25
Входной сигнал G(Z), выходной Y(Z) и сигнал рассогласования X(Z) записаны с использованием Z–преобразования.
Известна передаточная функция разомкнутой системы W(Z), также записанная с использованием Z–преобразования (3.24).
Если импульсная система содержит простейший импульсный элемент и апериодическое звено первого порядка с интегратором, то передаточная функция разомкнутой системы имеет вид
 где
где 
Для этой системы получена также передаточная функция замкнутой системы

По передаточной функции замкнутой системы можно записать уравнение системы
[Z2+(K1T–K1T1+K1T1d–d–1)Z+(K1T1–K1T1d–K1Td+d)]Y(Z) =
= K1[(T–T1+T1d)Z+(T1–T1d–Td)]G(Z). (3.28)
Обозначим 1=а0;
K1T–K1T1+K1T1d–d–1=a1;
K1T1–K1T1d–K1Td+d=a2;
K1(T–T1+T1d)=b0;
K1(T1–T1d–Td)=b1.
Перепишем уравнение в общем виде
(а0Z2+a1Z+a2)Y(Z)=(b0z+b1) G(Z) (3.29)
Для определения устойчивости системы нужно решить характеристическое уравнение
а0Z2+a1Z+a2=0. (3.30)
Известно, что корни характеристического уравнения Z1, Z2 можно представить на комплексной плоскости. Определим величины корней, при которых система будет устойчива.
Учитывая, что Z=epT, где p – оператор преобразования Лапласа, а для устойчивости системы по Ляпунову необходимо иметь отрицательные вещественные части корней характеристического уравнения системы, видим, что корни характеристического уравнения в области Z–преобразования должны лежать внутри единичной окружности.
Пусть имеем: Z1=α+jβ;
Z2=α–jβ.
Для устойчивости системы необходимо иметь
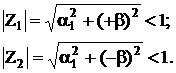 (3.31)
(3.31)
На комплексной плоскости корни лежат внутри единичной окружности (рис. 26).

Рис. 26
Если один из корней в области Z–преобразования будет расположен за пределами единичной окружности, то система станет неустойчивой.
При наличии корня │Z│=1 система будет находиться на границе устойчивости.
Определение: Импульсная система автоматического регулирования будет устойчива, если корни характеристического уравнения, записанного через Z–преобразование, будут лежать на комплексной плоскости внутри окружности единичного радиуса.
Пример.
Пусть в системе с простейшим импульсным элементом, апериодическими интегрирующими звеньями имеем: T1=0.1c, K1=10, T=0.01c.
Вычислим коэффициенты характеристического уравнения, записанного через Z–преобразование
а0=1;

a1=K1T–K1T1+K1T1d–d–1=0.1–1+0.9–0.9–1=–1.9;
a2=K1T1–K1T1d–K1Td=1–0.9–0.09+0.9=0.91.
Характеристическое уравнение:
Z2–1.9Z+0.91=0;
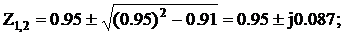
Z1=0.95+j0.087; Z2=0.95–j0.87;

Данная система устойчива.
Применим модифицированное w–преобразование
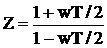
к характеристическому уравнению, записанному через Z–преобразование.
а0Z2+a1Z+a2=0.


После преобразований получим
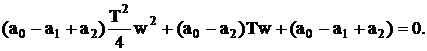 (3.32)
(3.32)
Обозначим
А0=(а0–a1+a2)T2/4;
А1=(a0–a2)T;
А2=(а0–a1+a2).
Получим новое характеристическое уравнение
А0w2+А1w+А2=0. (3.33)
Определим корни w1,2 полученного характеристического уравнения. По расположению корней w1,2 можно судить об устойчивости системы, пользуясь известными из линейной теории автоматического регулирования теоремами Ляпунова.
Определение: Импульсная система автоматического регулирования будет устойчива, если корни характеристического уравнения, записанного через w–преобразования, будут лежать в левой полуплоскости комплексной плоскости.
Пример.
Рассмотрим устойчивость уже исследованной системы, используя w–преобразование. Для этой системы получили:
а0=1;
a1=–1.9;
a2=0.91;
Т=0.01с.
Вычислим
А0=(а0–a1+a2)T2/4=(1+1.9+0.91)10-4/4=0.95∙10-4;
А1=(a0–a2)T=(1–0.91)∙0.01=0.9∙10-3;
А2=(а0–a1+a2)=1–1.9+0.91=0.01.
Характеристическое уравнение имеет вид
0.95∙10-4w2+0.9∙10-3w+0.01=0.
Вычислим корни уравнения

Видим, что вещественные части корней отрицательны –4.74<0, значит, система устойчива.
Пользуясь уравнением, записанным через w–преобразование, можно воспользоваться критериям Гурвица и Михайлова, а также следствиями из критерия Гурвица в обычных формулировках.
Для применения критерия Гурвица и его следствий рассмотрим характеристическое уравнение вида
А0w2+А1w+А2=0.
Матрица строится из коэффициентов А0, А1, А2 в виде
 (3.34)
(3.34)
Для устойчивости системы необходимо, чтобы
А0 > 0;
Δ1=|А1| > 0; (3.35)
Δ2=А1A2 > 0.
Пример.
Для рассмотренной системы имеем А0=0.95∙10-4;
А1=0.9∙10-3;
А2=0.01;

Δ1=|0.9·10-3|= 0.9·10-3;
Δ2=|0.9·10-3|·0.01=0.9·10-5.
Видим, что А0=0.95·10-4 > 0;
Δ1=0.9·10-3 > 0;
Δ2=0.9·10-5 > 0.
Значит, система устойчива.
В соответствии со 2–м следствием из критерия Гурвица для устойчивости системы достаточно в уравнении А0w2+А1w+А2=0 иметь положительные коэффициенты. В рассмотренном примере это имеет место, значит система устойчива.
Для применения критерия Михайлова следует рассмотреть многочлен
D(jω*)=A0(jω*)2+A1(jω*)+A2=X(ω*)+jY(ω*).
Построить кривую Михайлова в координатах Х,Y и определить угол поворота вектора D(jω) при изменении псевдочастоты ω* от 0 до ∞.
Аналогичным образом можно применить критерий Найквиста и логарифмический, построив АФХ или ЛАХи, как это указано в предыдущем параграфе.




 где
где 

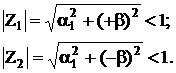 (3.31)
(3.31)

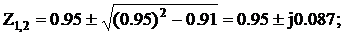

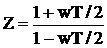


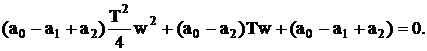 (3.32)
(3.32)
 (3.34)
(3.34)


