ВВЕДЕНИЕ
Логика – это наука о законах правильного мышления. Это одна из древнейших наук. Основные ее законы были сформулированы еще древнегреческим мыслителем Аристотелем. Идеи о построении логики на математической основе, т.е. по сути математической логики, были высказаны Лейбницем в начале 18-го века.
Современная математическая логика определяется как раздел математики, посвященный изучению математических доказательств и вопросов основания математики. Одна из главных причин широкого распространения математической логики – применение аксиоматического метода в построении различных математических теорий. Важным достижением математической логики является формулировка понятия алгоритмической вычислимости, которое по своей важности приближается к понятию натурального числа. Сегодня результаты математической логики находят свое применение в других отраслях математического знания, а также в программировании, проблемах искусственного интеллекта и других науках.
Данное учебно-практическое пособие соответствует учебной программе курса «Математическая логика и теория алгоритмов» для специальностей «Информационные системы и технологии», «Вычислительные машины, комплексы и сети».
Практикум разделен на три части. В первой содержится программа курса, во второй – краткое изложение теории и решение типовых задач, в третьей – задания для контрольных работ.
Достоинство практикума состоит в том, что при наличии такого количества задач он может быть использован как задачник, как раздаточный материал для выполнения контрольных работ, а также содержит не менее 30 различных вариантов индивидуального домашнего задания.
Студенты заочной формы обучения выполняют первые 10 вариантов контрольных заданий, например, 1-10, 39-49, выбирая задачи соответственно своему шифру.
ПРОГРАММА КУРСА МАТЕМАТИЧЕСКАЯ ЛОГИКА И ТЕРИЯ АЛГОРИТМОВ
Тема 1. «Совершенные дизъюнктивные нормальные формы, совершенные конъюнктивные нормальные формы». Формулы АВ. Эквивалентность формул АВ. Понятия ДНФ, КНФ, СДНФ, СКНФ.
Тема 2. «Логическое следствие в алгебре высказываний». Понятия логического следствия, противоречивого множества высказываний, тождественно истинного высказывания. Связь между этими понятиями.
Тема 3. «Исчисление высказываний (ИВ). Доказуемые формулы ИВ». Понятие исчисления. Язык ИВ. Определение формулы ИВ. Аксиомы и правила вывода ИВ. Доказуемые и выводимые формулы ИВ. Примеры доказуемых и выводимых формул ИВ.Теорема о дедукции в ИВ. Эквивалентные формулы ИВ.
Тема 4. «Логика предикатов (ЛП). Алгебраические системы. Подсистемы». Понятия сигнатуры, алгебраической системы данной сигнатуры, подсистемы, подсистемы, порожденной множеством. Примеры. Понятия терма данной сигнатуры, значение терма на кортеже в алгебраической системе. Теорема о подсистеме, порожденной множеством.
Тема 5. «Формулы ЛП». Понятие формулы данной сигнатуры. Определение истинности формулы ЛП на кортеже элементов в алгебраической системе. Примеры.
ТЕОРЕТИЧЕСКИЙ МАТЕРИАЛ
Совершенные дизъюнктивные нормальные формы, совершенные конъюнктивные нормальные формы
Эквивалентность формул АВ
Как показано в примере 1, различные формулы могут иметь одинаковые таблицы истинности. Так возникает понятие эквивалентности формул.
Формулы φ(x1,…,xn) и ψ(x1,…,xn) называются эквивалентными (φ ≡ ψ), если совпадают их таблицы истинности, т. е. ψ(е1,…,en) = φ(e1,…,en) для любых e1,…,en 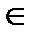 {0,1}
{0,1}
Пример 3. Построив таблицы истинности формул x→y и y→x, убеждаемся, что (х→y) ≡ (y→x).
Легко видеть, что отношение ≡ является отношением эквивалентности, т. е. оно рефлексивно (φ≡φ), симметрично (если φ≡ψ, то ψ≡φ),транзитивно (если φ≡ψ и ψ≡χ, то φ≡χ).
Отметим основные эквивалентности между формулами АВ:
1) φ∧φ≡φ, φ∨φ≡φ (законы идемпотентности);
2) φ∧ψ≡ψ∧φ, φ∨ψ≡ψ∨φ (законы коммутативности);
3) (φ∧ψ)∧χ≡φ∧(ψ∧χ), (φ∨ψ)∨χ≡φ∨(ψ∨χ) (законы ассоциативности);
4) φ∧(ψ∨χ)≡(φ∧ψ)∨(φ∧χ), φ∨(ψ∧χ)≡(φ∨ψ)∧(φ∨χ) (законы дистрибутивности)
5) (φ∧ψ)≡φ∨ψ, (φ∨ψ)≡φ∧ψ (законы де Моргана);
6) φ≡φ (закон двойного отрицания);
7) φ→ψ≡φ∨ψ;
8) φ∧(φ∨ψ)≡φ, φ∨(φ∧ψ)≡φ (законы поглощения);
9) φ∨(φ∧ψ)≡φ∨ψ, φ∨(φ∧ψ)≡φ∨ψ;
10) φ∧(φ∨ψ)≡φ∧ψ, φ∧(φ∨ψ)≡φ∧ψ.
Формула φ(x1,x2,…,xn) называется выполнимой (опровержимой), если существует такой набор значений переменных, на котором формула принимает значение 1 (соответственно 0).
Пример 4. Формула х∧у является одновременно выполнимой и опровержимой, поскольку 0∧0=0, а 1∧1=1.
Формула φ(x1,…,xn) называется тождественно истинной, общезначимой или тавтологией (тождественно ложной или противоречием), если эта формула принимает значение 1 (соответственно 0) на всех наборах значений переменных.
Пример 5. Формула x∨x является тождественно истинной, а формула x∧x — тождественно ложной:
Утверждение 1. Если формула φ1 тождественно истинна, φ0 — тождественно ложна, то для любых формул φ и ψ справедливы следующие эквивалентности:
1) φ∧ φ1≡φ; φ∨φ0≡φ;
2) φ∨φ1≡φ1; φ∧φ0≡φ0;
3) (φ∧ψ→φ)≡φ1; (φ→φ∨ψ)≡φ1.
Логическое следствие в АВ
Говорят, что формула ψ(х1,...,хп) АВ является логическим следствием формул φ1(х1,...,хп),…,φm(х1,...,хп) АВ (обозначается 
 ), если для любых
), если для любых  из соотношений
из соотношений 
 следует
следует  . Формулы
. Формулы  называются гипотезами.
называются гипотезами.
Пример 1. Доказать, что φ, φ→ψ, ψ→χ  Построим таблицы истинности для каждой формулы:
Построим таблицы истинности для каждой формулы:
Из таблицы истинности видно, что когда все гипотезы принимают значение равное 1, формула χ тоже принимает значение 1, значит, χ является логическим следствием, что и требовалось доказать.
Теорема 1.
1. Количество гипотез можно увеличивать.
2. Гипотезы можно переставлять в любом порядке.
3. 
 тогда и только тогда, когда
тогда и только тогда, когда 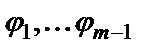

4. 
 тогда и только тогда, когда формула
тогда и только тогда, когда формула 
 тождественно истина.
тождественно истина.
5. 
 тогда и только тогда, когдаформула φ1∧..∧φm∧ψ тождественно ложна.
тогда и только тогда, когдаформула φ1∧..∧φm∧ψ тождественно ложна.
Исчисление высказываний
Пример 2.
1) Термами сигнатуры Σ={+,∙,≤,0} будут, например, 0, x, x+y, z(x+z)+0y, а x+y≤(0+х)x термом не является.
2) Если Σ={ƒ(3), g(1), h(2)}‑ функциональная сигнатура, то выражения h(ƒ(x1, x2, x3), g(x2)), g(ƒ(h(x1, x2), x1, g(x2)) – термы, а h(x1, ƒ(x1, x3)) не образует терм.
Пусть t(x1,…, xk)‑ терм из T(Σ), все переменные которого содержатся среди x1,…,xk; 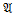 =(A,Σ) ‑ алгебраическая система. Значение терма t при значениях a1,…,ak
=(A,Σ) ‑ алгебраическая система. Значение терма t при значениях a1,…,ak 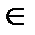 A переменных x1,…,xk(t(a1,…,ak)) определяется по индукции:
A переменных x1,…,xk(t(a1,…,ak)) определяется по индукции:
1) если t есть переменная xi (константный символ с), то значение t есть аi(с):
2) если терм t есть ƒ(t1,…, tn), а значения t1,…,tn суть b1,…,bn, то значение терма t есть ƒ(b1,…, tn).
Теорема 2. Если 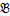 =(B,Σ) ‑ алгебраическая система, Ø≠x
=(B,Σ) ‑ алгебраическая система, Ø≠x 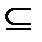 B, то носитель подсистемы
B, то носитель подсистемы 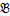 (Х) равен {t(a1,…,an) ׀ t
(Х) равен {t(a1,…,an) ׀ t 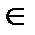 T(Σ), a1,…,an
T(Σ), a1,…,an 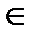 X}.
X}.
Доказательство. Индукцией по числу шагов построения терма t получаем, что если t(x1,x2,…,xn) 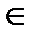 T(Σ) и a1,…,an
T(Σ) и a1,…,an 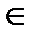 X, то t(a1,…,an)
X, то t(a1,…,an) 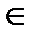 А для любой подсистемы
А для любой подсистемы 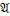
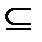
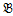 , содержащей X. Поэтому достаточно показать, что множество Y={t(a1,…,an) ׀ t
, содержащей X. Поэтому достаточно показать, что множество Y={t(a1,…,an) ׀ t 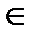 T(Σ), a1,…,an
T(Σ), a1,…,an 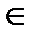 X } замкнуто относительно операций системы
X } замкнуто относительно операций системы 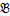 . Пусть ƒ(n)єT(Σ), t1,…,tm
. Пусть ƒ(n)єT(Σ), t1,…,tm 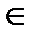 T(Σ), bi=t(a1,…,an), i
T(Σ), bi=t(a1,…,an), i 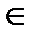 {1,…,m}. Тогда ƒ(b1,…,bm)
{1,…,m}. Тогда ƒ(b1,…,bm) 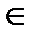 Y, поскольку ƒ(t1,…,tm)
Y, поскольку ƒ(t1,…,tm) 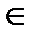 T(Σ).
T(Σ).
Таким образом, носитель подсистемы 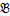 (X) состоит из всех элементов, которые получаются при подстановке элементов из X в термы.
(X) состоит из всех элементов, которые получаются при подстановке элементов из X в термы.
Пример 3.
1) Найдем носитель подсистемы 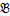 (Х) системы
(Х) системы 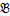 =(Q, ∙) для множества X={1/2}. Так как сигнатура Σ системы В есть {∙}, то Т(Σ)={x1, x1x2, (x1x2)x3, x1(x2x3),…}. По теореме 2 получаем B(X)={1/2, 1/2∙1/2, 1/2∙1/2∙1/2,…}={1/2, 1/8, 1/16,…}={1/2n,n≥1}.
=(Q, ∙) для множества X={1/2}. Так как сигнатура Σ системы В есть {∙}, то Т(Σ)={x1, x1x2, (x1x2)x3, x1(x2x3),…}. По теореме 2 получаем B(X)={1/2, 1/2∙1/2, 1/2∙1/2∙1/2,…}={1/2, 1/8, 1/16,…}={1/2n,n≥1}.
2)Если 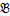 =(Q\{0},.,:) X={1/2}, то, поскольку по сравнению с предыдущим примером сигнатура дополняется операцией деления, множество В(Х) содержит числа 1/2n:1/2m=2m-n, m, n≥1, т.е. C={2n ׀ nєZ}
=(Q\{0},.,:) X={1/2}, то, поскольку по сравнению с предыдущим примером сигнатура дополняется операцией деления, множество В(Х) содержит числа 1/2n:1/2m=2m-n, m, n≥1, т.е. C={2n ׀ nєZ} 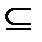 B(X). Так как множество С замкнуто относительно операций умножения и деления. т.е. (C, Σ) является подсистемой системы
B(X). Так как множество С замкнуто относительно операций умножения и деления. т.е. (C, Σ) является подсистемой системы 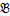 и содержит множество X, то В(Х)
и содержит множество X, то В(Х) 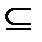 С. Следовательно, B(Х)=С.
С. Следовательно, B(Х)=С.
Пример 4. Построить подсистему алгебраической системы А, порожденную множеством Х.
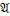 =
= 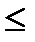 Z; -
Z; - 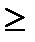
X={22;-36}.
Решение. Надо определить какую подсистему порождают
22;-36 “-“. Таке как 2=22-8  (-36)-14
(-36)-14  22 и любое число, получаемое из чисел 22, -36 с помощью операции вычитания четное, то
22 и любое число, получаемое из чисел 22, -36 с помощью операции вычитания четное, то
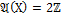
Пример 5. Построить подсистему алгебраической системы 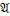 , порожденнуюмножеством Х.
, порожденнуюмножеством Х.
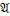 =
= 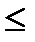 R\{0};:
R\{0};: 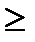
Х={ 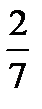 ;
; 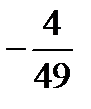 }.
}.
Решение.
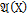 ={
={ 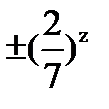 z
z 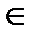 }.
}.
Формулы ЛП
Большинство определений этого параграфа будут индуктивными.
Введем понятие атомарной формулы сигнатуры Σ:
1) если t1, t2, 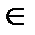 T(Σ), то t1=t2 ‑ атомарная формула:
T(Σ), то t1=t2 ‑ атомарная формула:
2) если P(n) 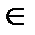 Σ ‑предикатный символ, t1,t2,…,tn
Σ ‑предикатный символ, t1,t2,…,tn 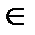 T(Σ), то Р(t1,t2,…,tn) ‑ атомарная формула;
T(Σ), то Р(t1,t2,…,tn) ‑ атомарная формула;
3) никаких атомарных формул, кроме построенных по пп. 1, 2, нет.
Формула сигнатуры Σ определяется следующим образом:
1) атомарная формула есть формула;
2) если φ, ψ - формулы, то φ, (φ∧ψ), (φ∨ψ), (φ→ψ),  xφ,
xφ,  xφ ‑ формулы;
xφ ‑ формулы;
3) никаких формул, кроме построенных по пп. 1, 2, нет.
Символы  ,
,  использованные в определении, называются соответственно квантором всеобщности и квантором существования и читаются "для любого"и "существует". Все соглашения относительно расстановок скобок, принятые в алгебре высказываний, остаются в силе и для формул логики предикатов. Кроме того, вместо записей
использованные в определении, называются соответственно квантором всеобщности и квантором существования и читаются "для любого"и "существует". Все соглашения относительно расстановок скобок, принятые в алгебре высказываний, остаются в силе и для формул логики предикатов. Кроме того, вместо записей  x1…
x1…  xnφ и
xnφ и  x1…
x1…  xnφ будем использовать записи
xnφ будем использовать записи  x1,…,xnφ и
x1,…,xnφ и  x1,…,xnφ.
x1,…,xnφ.
Определим подформулы формулы φсигнатуры Σ:
1) если φ‑ атомарная формула, то φ ‑ ее единственная
подформула;
2) если φ имеет вид φ1, или  xφ1,или
xφ1,или  xφ1, то подформула формулы φ – этолибо φ, либо подформула формулы φ1;
xφ1, то подформула формулы φ – этолибо φ, либо подформула формулы φ1;
3) если φ имеет вид φ1∧φ2, или φ1∨φ2, или φ1→φ2, то подформула формулы φ‑ это либо φ, либо подформула формулы φ1, либо подформула формулы φ2;
4) других подформул формулы φ, кроме построенных по
пп. 1, 2, 3, нет.
Пример 1. Пусть Σ={F(2),P(1)}, φ=  x(
x( y(x=F(z,y))∨P(z)) ‑ формула сигнатуры Σ. Тогда
y(x=F(z,y))∨P(z)) ‑ формула сигнатуры Σ. Тогда  x(
x( y(x=F(z,y))∨P(z)),
y(x=F(z,y))∨P(z)),  y(x=F(z,y))∨P(z),
y(x=F(z,y))∨P(z),  y(x=F(z,y)),x=F(z,y)),P(z)‑ все подформулы формулы φ.
y(x=F(z,y)),x=F(z,y)),P(z)‑ все подформулы формулы φ.
Говорят, что вхождение переменной х в формулу φ связано в φ, если оно находится в терме или предикате подформулы формулы φ вида  xψ или
xψ или  xψ; в противном случае это вхождение называется свободным в φ. Переменная х называется свободной (связанной), если некоторое вхождение х в φ свободно (связано).
xψ; в противном случае это вхождение называется свободным в φ. Переменная х называется свободной (связанной), если некоторое вхождение х в φ свободно (связано).
Пример 2. Пусть S={P1(1),P2(2)}. Рассмотрим формулы:
1) P1(x);
2) Р2(x,y)→  xP1(x);
xP1(x);
3)  x(P2(x,y)→P1(x)).
x(P2(x,y)→P1(x)).
Переменная х в первой формуле является свободной, во второй - и свободной, и связанной, в третьей ‑ связанной: переменная у во всех формулах свободна.
Пример 3.
Выписать все подформулы формулы φ, определить свободные и связанные вхождения переменных.
φ 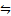
 x
x  z
z  y(x
y(x 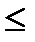 y+z)
y+z)  ((z∙2=u)→
((z∙2=u)→  u(u=x+z)).
u(u=x+z)).
Определить все свободные и связанные переменные формулы φ.
Решение. Выпишем подформулыформулы φ.
1) x 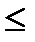 y+z,
y+z,
2)  y(x
y(x 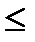 y+z),
y+z),
3)  z
z  y(x
y(x 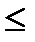 y+z),
y+z),
4)  x
x  z
z  y(x
y(x 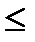 y+z),
y+z),
5) z  2=u,
2=u,
6) u=x+z,
7)  u(u=x+z),
u(u=x+z),
8) (z  2=u)→
2=u)→  u(u=x+z),
u(u=x+z),
9) φ.
Поскольку существуют связанные и свободные вхождения переменной х в формулу φ, то х является связанной и свободной переменной. Переменныеuи zтоже связанные и свободные. Переменнаяy связанная.
Предложением или замкнутой формулой сигнатуры Σ называется формула сигнатуры Σ, не имеющая свободных переменных.
Запись φ(x1,…,xn) будет означать, что все свободные переменные формулы φ содержатся в множестве {x1,…, xn}.
Пример 1.
Записать формулу φ(x), истинную в 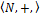 тогда и только тогда, когда х четно.
тогда и только тогда, когда х четно.
Решение.
φ(x)=  y(x=y+y).
y(x=y+y).
Пример 2.
Записать формулу φ'(x,y,z), истинную в 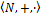 тогда и только тогда, когда z‑ наименьшее общее кратное чисел х и y.
тогда и только тогда, когда z‑ наименьшее общее кратное чисел х и y.
Решение.
φ'(x,y,z)=ψ(x,y,z)∧χ(x,y,z), где формула ψ «говорит» о том, что z делится на x и на y, а формула χ "говорит"о том, что z делит все общие кратные х и у, т. е. является наименьшим из всех общих кратных:
ψ=  u,∨(z=u∙x∧z=∨х∙y),
u,∨(z=u∙x∧z=∨х∙y),
χ=  w(
w( u,∨(w=u∙x∧w=∨х∙y)→
u,∨(w=u∙x∧w=∨х∙y)→  w1(w=w1∙z)). Итак,
w1(w=w1∙z)). Итак,
φ'(х,у,z)=  u,∨(z=u∙x∧z=х∙y)∧
u,∨(z=u∙x∧z=х∙y)∧  w(
w( u,∨(w=ux∧w=хy)→
u,∨(w=ux∧w=хy)→  w1(w=w1z)).
w1(w=w1z)).
Логическое следствие в ЛП
Через  обозначим кортеж переменных
обозначим кортеж переменных 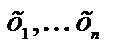 ; через
; через 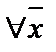 ‑
‑ 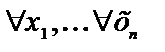 .
.
Определение. Пусть φ1( ),…,φn(
),…,φn( ), ψ(
), ψ( ) – формулы сигнатуры ∑. Формула ψ называется логическим следствием формул φ1,…,φn (обозначается φ1,…,φn╞ ψ), если для любой алгебраической системы
) – формулы сигнатуры ∑. Формула ψ называется логическим следствием формул φ1,…,φn (обозначается φ1,…,φn╞ ψ), если для любой алгебраической системы 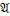 сигнатуры ∑
сигнатуры ∑
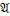 ╞
╞ 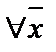 (φ1(
(φ1( )
)  …
…  φn(
φn( )→ψ(
)→ψ( )).
)).
Пример 1.
Доказать, что φ1( )→φ2(
)→φ2( ),φ2(
),φ2( )→φ3(
)→φ3( )╞φ1(
)╞φ1( )→φ3(
)→φ3( ) (1)
) (1)
где φ1( ),φ2(
),φ2( ),φ3(
),φ3( ) – формулы сигнатуры ∑.
) – формулы сигнатуры ∑.
Пусть 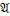 =‹А, ∑› ‑ произвольная система сигнатуры ∑. Необходимо указать, что
=‹А, ∑› ‑ произвольная система сигнатуры ∑. Необходимо указать, что 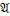 ╞
╞ 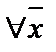 ((φ1(
((φ1( )→φ2(
)→φ2( ))
))  ((φ2(
((φ2( )→φ3(
)→φ3( ))→(φ1(
))→(φ1( )→φ3(
)→φ3( ))).
))).
Пусть 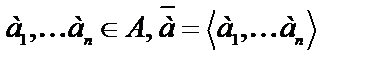 и
и 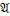 ╞ ((φ1(
╞ ((φ1(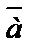 )→φ2(
)→φ2(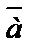 ))
))  ((φ2(
((φ2(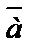 )→φ3(
)→φ3(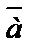 )).
)).
Покажем, что 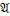 ╞(φ1(
╞(φ1(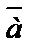 )→φ3(
)→φ3(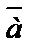 ) (2)
) (2)
Предположим, что 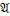 ╞φ1(
╞φ1(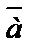 ). Так как
). Так как 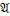 ╞(φ1(
╞(φ1(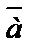 )→φ2(
)→φ2(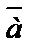 ), то
), то 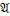 ╞φ2(
╞φ2(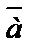 ).
).
Так как 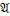 ╞φ2(
╞φ2(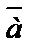 )→φ3(
)→φ3(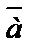 ), то
), то 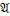 ╞φ3(
╞φ3(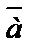 ).
).
Таким образом (2), а, следовательно, и (1), доказано.
Исчисление предикатов
Зафиксируем некоторую произвольную сигнатуру Σ и определим исчисление предикатов сигнатуры Σ (ИПΣ).
Формулами ИПΣ будут формулы сигнатуры Σ.
Примем следующие соглашения. Пусть x1,…,xn ‑ переменные, t1,…,tn ‑ термы сигнатуры Σ и φ ‑ формула сигнатуры Σ. Запись  будет обозначать результат подстановки термов t1,…,tn вместо всех свободных вхождений в φ переменных x1,…,xn соответственно, причем, если в тексте встречается запись
будет обозначать результат подстановки термов t1,…,tn вместо всех свободных вхождений в φ переменных x1,…,xn соответственно, причем, если в тексте встречается запись 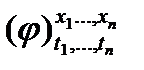 , то предполагается, что для всех i={1,...,n} ни одно свободное вхождение в φ переменной xi не входит в подформулу φвида
, то предполагается, что для всех i={1,...,n} ни одно свободное вхождение в φ переменной xi не входит в подформулу φвида  y
y 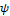 или
или  y
y 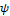 , где у - переменная, входящая в ti.
, где у - переменная, входящая в ti.
Аксиомами ИПΣ являются аксиомы вида 1-10 ИВ, а также аксиомы
11)  xφ→(φ)tx;
xφ→(φ)tx;
12) (φ)tx→ 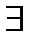 xφ;
xφ;
13) x=x;
14) x=y→((φ)xz→(φ)yz).
Формулы 1-14 называются схемами аксиом ИПΣ.
Правила вывода ИПΣ:
1. φ, φ → ψ,
ψ
2. ψ →φ,
ψ→  xφ
xφ
3. φ → ψ,
 xφ → ψ
xφ → ψ
где в правилах 2 и 3 переменная x не входит свободно в ψ.
Доказательством в ИПΣ формулы φ называется такая последовательность φ0,…,φn формул ИПΣ, что φn 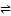 φ и для каждого i≤n формула φi удовлетворяет одному из следующих условий:
φ и для каждого i≤n формула φi удовлетворяет одному из следующих условий:
1) φi ‑аксиома ИПΣ;
2) φi получается из некоторых φ1,…, φi-1, по одному из правил вывода 1-3.
Если существует доказательство в ИПΣ формулы φ, то φ называется доказуемой в ИПΣ или теоремой ИПΣ (обозначаем ├φ).
Выводом в ИПΣформулы φ из множества формул φ1,…, φm называется такая последовательность ψ1,…,ψk формул ИПΣ, что φn 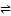 φ и для каждого i≤n формула φi удовлетворяет одному из следующих условий:
φ и для каждого i≤n формула φi удовлетворяет одному из следующих условий:
1) φi ‑аксиома ИПΣ;
2) φi принадлежит Г;
3) φi получается из некоторых ψ1,…, ψi-1 j<i, по одному из правил вывода 1-3, причем при применении правил 2 и 3 переменная х не должна входить ни в одну формулу из Г свободно.
Если существует вывод в ИПΣ формулы φ из множества формул φ1,…, φn, то φ называется выводимой в ИПΣ из Г (обозначаем Г├φ). При этом Г называется множеством гипотез. Очевидно, что доказуемость формулы эквивалентна ее выводимости из пустого множества гипотез. Так же, как в исчислении высказываний, определяется понятие квазивывода. Если Г = {ψ1,…,ψn}, то вместо Г├φ пишем ψ1,…,ψn├φ.
Формула ψ сигнатуры Σ называется тавтологией, если она получается из формулы φ исчисления высказываний, доказуемой в исчислении высказываний, путем замены всех ее пропозициональных переменных x1,…,xn на формулы ψ1,…,ψn сигнатуры Σ соответственно. Формулу φ при этом называют основой тавтологии.
Утверждение 1. Любая тавтология φ сигнатуры Σ доказуема в ИПΣ.
Следствие 1. Если φ и ψ ‑ пропозиционально эквивалентные формулы сигнатуры Σ, то φ и ψ‑ эквивалентные формулы сигнатуры Σ.
В исчислении предикатов ИПΣ справедлива теорема о дедукции.
Теорема 1. (о дедукции).Пусть Г – множество формул ИПΣ, φ, ψ – формулы ИПΣ. Тогда Г,φ├ψ,  Г├φ→ψ.
Г├φ→ψ.
Эквивалентные формулыИП
Определение эквивалентных формул, утверждения 3,4 при замене формул φ, ψ, χ ИВ на формулы ИПΣ имеют место.
Утверждение 1. В ИПΣ выполнимы все эквивалентности ИВ из теоремы 5.
Доказательство. Выполнимость в ИПΣ всех эквивалентностей исчисления высказываний следует из следствия 3.
Утверждение 2. В ИПΣ выполнимы следующие эквивалентности, в которых предполагается, что переменная ж не входит свободно в формулу ψ, а переменная у не входит в формулу φ:
1)  xφ≡
xφ≡  xφ,1\)
xφ,1\)  xφ≡
xφ≡  xφ,
xφ,
2)  x(φ∧ψ)≡
x(φ∧ψ)≡  xφ∧ψ, 2\)
xφ∧ψ, 2\)  x(φ∨ψ)≡
x(φ∨ψ)≡  xφ∨ψ
xφ∨ψ
3)  x(φ∧ψ)≡
x(φ∧ψ)≡  xφ∧ψ, 3\)
xφ∧ψ, 3\)  x(φ∨ψ)≡
x(φ∨ψ)≡  xφ∨ψ,
xφ∨ψ,
4)  xφ≡
xφ≡ 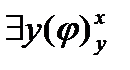 . 4\)
. 4\)  xφ≡
xφ≡ 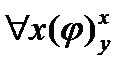
Пример. 1. Докажем эквивалентность а). Построим квазивывод формулы  xφ→
xφ→  xφ из Ø:
xφ из Ø:
1. φ→  xφ ‑ аксиома 12;
xφ ‑ аксиома 12;
2.  xφ→φ ‑ к п.1 применили утверждение 3:
xφ→φ ‑ к п.1 применили утверждение 3:
3.  xφ→
xφ→  xφ ‑ к п.2 применили правило вывода 2.
xφ ‑ к п.2 применили правило вывода 2.
Построим квазивывод формулы  xφ→
xφ→  xφ из Ø:
xφ из Ø:
1.  xφ→φ ‑ аксиома 11;
xφ→φ ‑ аксиома 11;
2. φ→  xφ ‑ к п.1 применили утверждение 3;
xφ ‑ к п.1 применили утверждение 3;
3.  xφ→
xφ→  xφ ‑ к п. 2 применили правило вывода 3;
xφ ‑ к п. 2 применили правило вывода 3;
4.  xφ→
xφ→  xφ ‑ к п.З применили утверждение 3.
xφ ‑ к п.З применили утверждение 3.
Пример. 2. Докажем эквивалентность г). Построим квазивывод формулы  x(φ∧ψ)→
x(φ∧ψ)→  xφ∧ψ из Ø:
xφ∧ψ из Ø:
1.  x(φ∧ψ)→φ∧ψ ‑ аксиома 11;
x(φ∧ψ)→φ∧ψ ‑ аксиома 11;
2. φ∧ψ→φ ‑ утверждение 1;
3.  x(φ∧ψ)→φ ‑ к пп.1,2 применили утверждение 1;
x(φ∧ψ)→φ ‑ к пп.1,2 применили утверждение 1;
4.  x(φ∧ψ)→
x(φ∧ψ)→  xφ ‑ к п.4 применили правило вывода 2;
xφ ‑ к п.4 применили правило вывода 2;
5. φ∧ψ→ψ ‑ утверждение 1;
6.  x(φ∧ψ)→ψ ‑ к пп.1,5 применили утверждение 1;
x(φ∧ψ)→ψ ‑ к пп.1,5 применили утверждение 1;
7. ( x(φ∧ψ)→
x(φ∧ψ)→  xφ)→((
xφ)→(( x(φ∧ψ)→ψ)→(
x(φ∧ψ)→ψ)→( x(φ∧ψ)→
x(φ∧ψ)→  xφ∧ψ)) ‑ аксиома 5;
xφ∧ψ)) ‑ аксиома 5;
8.  x(φ∧ψ)→
x(φ∧ψ)→  xφ∧ψ ‑ к пп.4.6.7 применили правило вывода 1.
xφ∧ψ ‑ к пп.4.6.7 применили правило вывода 1.
Построим квазивывод формулы  xφ∧ψ →
xφ∧ψ →  x (φ∧ψ) из Ø:
x (φ∧ψ) из Ø:
1.  xφ∧ψ→
xφ∧ψ→  xφ ‑ аксиома 3;
xφ ‑ аксиома 3;
2.  xφ→φ‑ аксиома 11;
xφ→φ‑ аксиома 11;
3.  xφ∧ψ→φ ‑ к пп.1,2 применили утверждение 1;
xφ∧ψ→φ ‑ к пп.1,2 применили утверждение 1;
4.  xφ∧ψ→ψ‑ аксиома 4;
xφ∧ψ→ψ‑ аксиома 4;
5. ( xφ∧ψ→φ)→((
xφ∧ψ→φ)→(( xφ∧ψ→ψ)→(
xφ∧ψ→ψ)→( xφ∧ψ→φ∧ψ)) ‑ аксиома 5;
xφ∧ψ→φ∧ψ)) ‑ аксиома 5;
6.  xφ∧ψ→φ∧ψ ‑ к пп.3,4,5 применили правило вывода 1;
xφ∧ψ→φ∧ψ ‑ к пп.3,4,5 применили правило вывода 1;
7.  xφ∧ψ→
xφ∧ψ→  x(φ∧ψ)‑ к п.6 применили правило вывода 2.
x(φ∧ψ)‑ к п.6 применили правило вывода 2.
Теорема 1. (теорема о замене). Если формула φ сигнатуры Σ получается из формулы ψ сигнатуры Σ заменой некоторого вхождения подформулы ψ' на формулу φ' сигнатуры Σ и φ'≡ψ', то φ≡ψ.
Машины Тьюринга
Машина Тьюринга 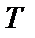 – это система, работающая в дискретные моменты времени
– это система, работающая в дискретные моменты времени 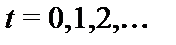 и состоящая из следующих частей:
и состоящая из следующих частей:
конечная лента,разбитая на конечное число ячеек.В каждый момент времени 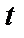 в ячейках записаны буквы из некоторого алфавита
в ячейках записаны буквы из некоторого алфавита 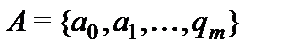 (где
(где 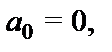
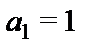 ,
, 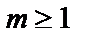 ), называемого внешним алфавитом машины.Ячейка, в которой записан символ
), называемого внешним алфавитом машины.Ячейка, в которой записан символ 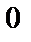 , называется пустой. Если в какой–то момент времени лента имеет
, называется пустой. Если в какой–то момент времени лента имеет 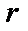 ячеек, то состояние ленты полностью описывается словом
ячеек, то состояние ленты полностью описывается словом 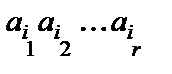 , где
, где 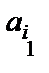 – состояние первой (слева) ячейки,
– состояние первой (слева) ячейки, 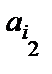 – состояние второй ячейки и т.д.
– состояние второй ячейки и т.д.
Управляющая головка, представляющая собой устройство, которое может перемещаться вдоль ленты так, что в каждый рассматриваемый момент времени оно находится напротив определенной ячейки и имеет некоторое состояние 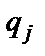 из конечного множества внутренних состояний
из конечного множества внутренних состояний 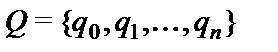 ,
, 
|
|
|



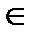 {0,1}
{0,1}
 ), если для любых
), если для любых  из соотношений
из соотношений 
 следует
следует  . Формулы
. Формулы  называются гипотезами.
называются гипотезами. Построим таблицы истинности для каждой формулы:
Построим таблицы истинности для каждой формулы: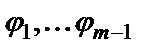

 тождественно истина.
тождественно истина.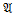 =(A,Σ) ‑ алгебраическая система. Значение терма t при значениях a1,…,ak
=(A,Σ) ‑ алгебраическая система. Значение терма t при значениях a1,…,ak 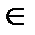 A переменных x1,…,xk(t(a1,…,ak)) определяется по индукции:
A переменных x1,…,xk(t(a1,…,ak)) определяется по индукции: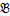 =(B,Σ) ‑ алгебраическая система, Ø≠x
=(B,Σ) ‑ алгебраическая система, Ø≠x 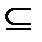 B, то носитель подсистемы
B, то носитель подсистемы 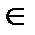 T(Σ), a1,…,an
T(Σ), a1,…,an 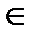 X}.
X}.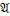
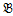 , содержащей X. Поэтому достаточно показать, что множество Y={t(a1,…,an) ׀ t
, содержащей X. Поэтому достаточно показать, что множество Y={t(a1,…,an) ׀ t 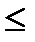 Z; -
Z; - 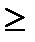
 (-36)-14
(-36)-14 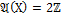
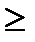
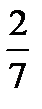 ;
; 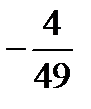 }.
}.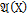 ={
={ 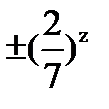 z
z  xφ,
xφ,  xφ ‑ формулы;
xφ ‑ формулы;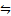
 ((z∙2=u)→
((z∙2=u)→  2=u,
2=u,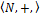 тогда и только тогда, когда х четно.
тогда и только тогда, когда х четно.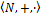 тогда и только тогда, когда z‑ наименьшее общее кратное чисел х и y.
тогда и только тогда, когда z‑ наименьшее общее кратное чисел х и y. обозначим кортеж переменных
обозначим кортеж переменных 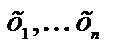 ; через
; через 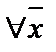 ‑
‑ 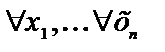 .
. …
…  φn(
φn(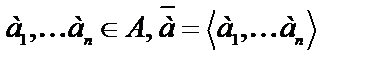 и
и 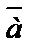 )→φ2(
)→φ2( будет обозначать результат подстановки термов t1,…,tn вместо всех свободных вхождений в φ переменных x1,…,xn соответственно, причем, если в тексте встречается запись
будет обозначать результат подстановки термов t1,…,tn вместо всех свободных вхождений в φ переменных x1,…,xn соответственно, причем, если в тексте встречается запись 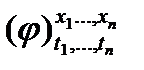 , то предполагается, что для всех i={1,...,n} ни одно свободное вхождение в φ переменной xi не входит в подформулу φвида
, то предполагается, что для всех i={1,...,n} ни одно свободное вхождение в φ переменной xi не входит в подформулу φвида 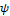 или
или 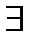 xφ;
xφ;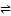 φ и для каждого i≤n формула φi удовлетворяет одному из следующих условий:
φ и для каждого i≤n формула φi удовлетворяет одному из следующих условий: Г├φ→ψ.
Г├φ→ψ.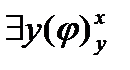 . 4\)
. 4\) 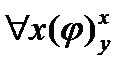
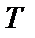 – это система, работающая в дискретные моменты времени
– это система, работающая в дискретные моменты времени 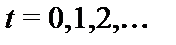 и состоящая из следующих частей:
и состоящая из следующих частей: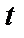 в ячейках записаны буквы из некоторого алфавита
в ячейках записаны буквы из некоторого алфавита 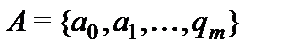 (где
(где 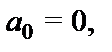
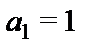 ,
, 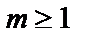 ), называемого внешним алфавитом машины.Ячейка, в которой записан символ
), называемого внешним алфавитом машины.Ячейка, в которой записан символ 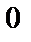 , называется пустой. Если в какой–то момент времени лента имеет
, называется пустой. Если в какой–то момент времени лента имеет 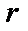 ячеек, то состояние ленты полностью описывается словом
ячеек, то состояние ленты полностью описывается словом 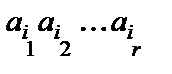 , где
, где 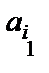 – состояние первой (слева) ячейки,
– состояние первой (слева) ячейки, 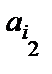 – состояние второй ячейки и т.д.
– состояние второй ячейки и т.д.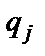 из конечного множества внутренних состояний
из конечного множества внутренних состояний 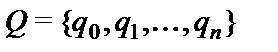 ,
, 


