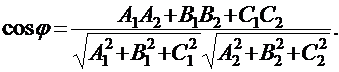ТЕОРЕТИКО – ПРАКТИЧЕСКИЙ КУРС
«ОСНОВЫ ЛИНЕЙНОЙ АЛГЕБРЫ
ДЛЯ ЭКОНОМИСТОВ И МЕНЕДЖЕРОВ»
Учебное пособие по курсу «Линейная алгебра»
Москва
Рекомендовано к изданию
Решением Ученого совета ИМЭС
(Протокол № 9 от 26 мая 2016 г.)
Настоящее учебное пособие разработал кандидат физико-математических наук, доцент, заведующий кафедрой математики и информатики ИМЭС Налимов Валерий Николаевич.
ПРЕДИСЛОВИЕ
Настоящее учебное пособие предназначено для студентов первого курса заочной формы обучения и по тематическому объему полностью соответствует требованиям рабочих программ учебной дисциплины «Линейная алгебра», которые, в свою очередь, полностью соответствуют требованиям действующих федеральных государственных образовательных стандартов по направлениям 38.03.01 “Экономика” и 38.03.02 “Менеджмент”.
Порядок изложения разделов, тем и основных подразделов тем в данном учебном пособии соответствует порядку, принятому в рабочих программах учебной дисциплины «Линейная алгебра» по соответствующему направлению подготовки. Однако нумерация тем и подразделов в настоящем пособии может отличаться от нумерации, принятой в учебном пособии [1].
По каждой теме и подразделу темы данное пособие содержит теоретический материал, изложенный в предельно сжатой форме (теоремы и аксиомы, математические факты, формулы и их следствия, имеющие практическую значимость), а также примеры использования этого материала для решения задач. В конце изложения теоретического материала каждой темы приведены вопросы для самопроверки знаний по этой теме курса. Некоторые темы курса заканчиваются вопросами в форме тестов.
После ознакомления с теоретическим материалом студенту следует кратко и четко ответить на вопросы, самостоятельно оценив и отобрав материал, изложенный в литературе, ссылки на которую приведены в конце каждой темы, или подраздела, а полный список литературы приводится в конце пособия. Ваши ответы должны быть размещены непосредственно в Вашем экземпляре пособия. Причем при тестовом варианте ответов на вопросы Вы должны поставить любой значок (крестик, галочку и т.п.) только в одном квадрате, соответствующем верному, на Ваш взгляд, ответу на поставленный вопрос.
Настоящее пособие может быть полезно и студентам 1 курса очно-заочного (вечернего), а также очного (дневного), отделений ИМЭС, при подготовке к сдаче экзаменов по дисциплине «Линейная алгебра».
ЛИСТ СТУДЕНТА
Фамилия ___________________________________
Имя ________________________________________
Отчество ____________________________________
Факультет ___________________________________
Курс _________________________________________
Группа _______________________________________
Дата начала работы: «_____» _____________ 20___ г.
Дата окончания работы «_____» ______________ 20___ г.
Личная подпись _________________________
ЛИСТ РЕЦЕНЗИИ
Рецензент ______________________
______________________
«_____» _______________ 20____ г.
ТЕМА 1. Матрицы и определители
Основные свойства определителей
1. При однократной перестановке двух строк (или столбцов) определитель меняет свой знак.
2. Умножение всех элементов какой-либо строки (или столбца) определителя на одно и то же число равносильно умножению всего определителя на это же число.
3. Если некоторая строка (или столбец) определителя целиком состоит из нулей, то этот определитель равен нулю.
4. Если элементы какой-либо строки (или столбца) определителя пропорциональны (в частном случае равны) соответствующим элементам другой строки (или столбца), то этот определитель равен нулю.
5. При транспонировании матрицы ее определитель не меняет своего значения, т.е. | АТ | = | А |.
6. Определитель не изменится, если к элементам какой-либо строки (столбца) прибавить соответствующие элементы другой строки (столбца), умноженные на любой множитель.
7. Определители верхней треугольной, нижней треугольной и диагональной матриц равны произведению элементов их главной диагонали.
8. Определитель произведения двух квадратных матриц равен произведению их определителей: | АВ | = | А |∙| В |, откуда следует: | АВ | = | ВА |.
Обратная матрица и обращение матриц
Определение. Матрица А-1 называется обратной для квадратной матрицы А, если выполняется равенство:
Определение. Если определитель квадратной матрицы отличен от нуля, то такая матрица называется невырожденной. Если же определитель матрицы равен нулю, то такая матрица называется вырожденной.
| Обратная матрица А-1 существует и единственна тогда и только тогда, когда исходная матрица А является невырожденной.
|
Алгоритм обращения матрицы
1. Вычислить определитель матрицы А. При этом обратная матрица будет существовать, только в случае | А | ≠ 0.
2. Транспонировать матрицу А, т.е. найти матрицу АТ.
3. Найти алгебраические дополнения всех элементов матрицы АТ и, расставив их на места соответствующих элементов, получить присоединенную к А матрицу  .
.
4. Найти матрицу обратную матрице А по формуле: 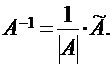
5. Проверить правильность вычислений, убедившись в справедливости любого из равенств 
ПРИМЕР: Найти матрицу, обратную матрице

1. Находим | А | = 10 ≠ 0, следовательно, матрица, обратная к матрице А существует.
2. Транспонируем матрицу А и найдем:

3. Последовательно найдем алгебраические дополнения всех элементов матрицы АТ и, расставив их на места элементов в матрице АТ, получим присоединенную к матрице А матрицу в виде:

4. Находим искомую матрицу:

5. Проверка показывает, что вычисления проведены правильно:

Алгоритм Гаусса (пошаговый)
Шаг 1. Если элемент а11 исходной матрицы равен нулю, т.е. а11 = 0, то перестановкой строк или столбцов матрицы добиваются того, чтобы элемент а11 полученной матрицы был отличен от нуля.
Шаг 2. Сложением первой строки (в ней а11 ≠ 0), умноженной на подходящие (различные для различных строк) множители, с другими строками добиваются того, чтобы все элементы первого столбца матрицы, стоящие ниже элемента а11 ≠ 0, т.е. элементы а21, а31, … были бы равны нулю.
Шаг 3. Теперь, либо уже получена ступенчатая матрица, либо в строках со второй по m -ую имеется по крайней мере один ненулевой элемент, который при помощи перестановки строк или столбцов (кроме первой строки и первого столбца) может быть поставлен на второе по порядку место в главной диагонали, т.е. на место элемента а22. После этого снова выполняют операции, аналогичные шагу 2, но сложение осуществляют уже со второй строкой, и в результате получают, что все элементы второго столбца, стоящие ниже элемента а22 равны нулю и т.д. и т.д.
Аналогичные перечисленным операции применяются и к последующим строкам матрицы, а сам процесс продолжают до тех пор, пока не получат искомую, ступенчатую матрицу. Если в процессе выполнения таких операций на каком-то шаге получается нулевая строка, то ее вычеркивают.
ПРИМЕР: Найти ранг матрицы 
Решение. Убедившись, что для данной матрицы элемент а11 = 1 ≠ 0, сразу переходим к шагу 2. Умножив первую строку матрицы на число (- 2), сложив ее со второй строкой и записав результат во вторую строку, а также сложив первую строку матрицы с третьей строкой и записав результат в третью строку, получим матрицу вида:

Убедившись, что в полученной после 2 шага матрице элемент а22 = 7 ≠ 0, переходим к реализации шага 3, для чего умножим вторую строку этой матрицы на число 1/7 и сложим ее с третьей строкой, в результате получим:

У полученной ступенчатой матрицы третья, нулевая строка может быть вычеркнута без изменения ранга этой матрицы. Оставшаяся матрица имеет размер 2 ´ 4 и также является ступенчатой. Очевидно, что полученная ступенчатая матрица имеет две ступеньки (две строки), а, следовательно, ранг ее равен 2 и, следовательно, ранг исходной матрицы также равен 2.
Рекомендуемая литература по теме 1: [1 – 3].
Метод обратной матрицы
Если в системе линейных уравнений число уравнений равно числу неизвестных и матрица системы А является невырожденной, т.е. | А | ≠ 0, то для матрицы системы существует обратная матрица А-1.
Запишем такую систему в матричном виде: AX = B. Умножая слева обе части этого матричного равенства на матрицу А-1, получим: A-1 (AX) = A-1B. Так как (A-1A) X = EX = X, то решением системы будет матрица-столбец:

ПРИМЕР: Для системы уравнений:

определитель матрицы системы | А | = 5 ≠ 0 (убедитесь в этом сами). Следовательно, обратная матрица для матрицы А существует и имеет вид:

Поэтому решением данной системы будет матрица-столбец:
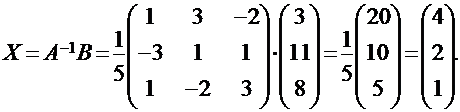
Правило Крамера
Предположим, что матрица системы А является квадратной, а ее определитель Δ0 = | А | ≠ 0. Тогда единственное решение системы может быть найдено по формулам Крамера:

где Δ j – определитель матрицы, полученной из матрицы системы заменой j –го столбца на столбец свободных членов.
ПРИМЕР: Решим с использованием формул Крамера систему примера в подразделе 2.2.1. Здесь Δ0 = | А | = 5,

И по формулам Крамера получим:


Метод Гаусса
Методы, рассмотренные в предыдущих подразделах, применимы только когда число уравнений равно числу неизвестных. Однако существует универсальный метод решения таких систем, применимый при любом соотношении между числом уравнений и числом неизвестных – метод Гаусса.
Для любой системы линейных уравнений можно составить расширенную матрицу системы, которая отличается от матрицы системы тем, что справа добавляется еще один столбец – столбец свободных членов, который для удобства принято отделять вертикальной чертой. В общем случае расширенная матрица системы имеет вид:

Метод Гаусса заключается в том, что с помощью элементарных преобразований строк расширенная матрица системы приводится к ступенчатому виду. Система линейных уравнений, соответствующая этой матрице, будет эквивалентна исходной системе. Для системы уравнений, составленной по ступенчатой матрице, все решения могут быть найдены последовательно, начиная с последнего уравнения.
Теорема Кронекера – Капелли
| Система линейных уравнений совместна только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы.
|
ПРИМЕР: Проверьте совместность системы линейных уравнений:

Для сравнения рангов матриц составим расширенную матрицу системы и приведем ее к ступенчатому виду:

Рассматривая полученную ступенчатую матрицу, имеющую только две ступеньки, можно сделать вывод, что ранг матрицы системы равен рангу расширенной матрицы системы и равен 2. Согласно критерию, данная система уравнений – совместна.
Переход к новому базису
Пусть в пространстве R имеется два базиса: «старый»  и «новый»
и «новый»  . Очевидно, что каждый из векторов нового базиса можно представить в виде линейной комбинации векторов старого базиса:
. Очевидно, что каждый из векторов нового базиса можно представить в виде линейной комбинации векторов старого базиса:
 (*)
(*)
Это же представление можно записать в матричной форме:
Полученная запись означает, что переход от старого базиса к новому задается матрицей перехода А. Эта матрица, как и матрица АТ невырожденная, т.к. в противном случае ее строки (а, следовательно, и базисные векторы) оказались бы линейно зависимы.
Найдем зависимость между координатами одного и того же вектора в разных базисах. Пусть некоторый вектор  имеет координаты
имеет координаты  относительно старого базиса и координаты
относительно старого базиса и координаты  относительно нового базиса, т.е. можно записать:
относительно нового базиса, т.е. можно записать:

Если теперь подставить в среднюю часть этих равенств выражения для векторов  из равенств (*), то после несложных преобразований можно получить:
из равенств (*), то после несложных преобразований можно получить:
 (**)
(**)
Систему представлений (**) можно записать и в матричной форме, т.е. в виде: Х = А∙Х*,именно так координаты вектора в старом базисе выражаются через координаты того же вектора в новом базисе.
Если решить систему уравнений (**) методом обратной матрицы (это можно сделать, т.к. матрица A невырожденная, и обратная ей матрица существует), то получим: Х* = А-1Х именно таким образом координаты вектора в новом базисе выражаются через координаты того же вектора в старом базисе.
ПРИМЕР: Найдите координаты вектора  в новом базисе
в новом базисе  примера подраздела 3.3.
примера подраздела 3.3.
Используя разложения векторов  по векторам базиса, приведенные в условии примера подраздела 3.3, можно матрицу перехода от старого базиса к новому записать в виде:
по векторам базиса, приведенные в условии примера подраздела 3.3, можно матрицу перехода от старого базиса к новому записать в виде:
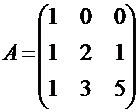 .
.
Можно убедиться в том, что определитель этой матрицы | А | = 7 ≠ 0. Поэтому существует обратная ей матрица, которая имеет вид (убедитесь в этом самостоятельно):

Для отыскания координат вектора  в новом базисе
в новом базисе  воспользуемся формулой: Х* = А-1Х и найдем:
воспользуемся формулой: Х* = А-1Х и найдем:

Таким образом разложение вектора по векторам нового базиса можно записать в виде: 
Евклидово пространство
Выше мы ввели понятие линейного векторного пространства, в котором определены операции сложения векторов и умножения их на число, а также ввели понятия размерности и базиса этого пространства. Теперь дополним это пространство метрикой, т.е. укажем способы измерения длин векторов и углов между ними. Это можно сделать, доопределив в векторном пространстве понятие скалярного произведения векторов, естественно, обобщив его на случай n -мерных векторов.
Определение. Скалярным произведением двух векторов  и
и  называется число, равное:
называется число, равное:

Отметим основные свойства скалярного произведения, которые непосредственно вытекают из сформулированного определения.
1.  - коммутативное свойство;
- коммутативное свойство;
2.  - дистрибутивное свойство;
- дистрибутивное свойство;
3.  - свойство справедливое для любого действительного α;
- свойство справедливое для любого действительного α;
4.  , если
, если  , и
, и  , если
, если  .
.
Определение. Линейное векторное пространство, в котором определено скалярное произведение векторов, удовлетворяющее указанным четырем свойствам, рассматриваемым как аксиомы, называется евклидовым пространством.
Определение. Длиной или нормой вектора  в n -мерном евклидовом пространстве называется корень квадратный из его скалярного квадрата, т.е.:
в n -мерном евклидовом пространстве называется корень квадратный из его скалярного квадрата, т.е.:

Определенная таким образом норма вектора обладает некоторыми свойствами, основное из которых записывается в виде:  и носит название неравенства Коши-Буняковского.
и носит название неравенства Коши-Буняковского.
Очевидно, что косинус угла j между двумя векторами  и
и 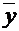 можно определить равенством, непосредственно вытекающим из неравенства Коши-Буняковского:
можно определить равенством, непосредственно вытекающим из неравенства Коши-Буняковского:
 , где:
, где: 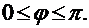
Определение. Два вектора называются ортогональными, если их скалярное произведение равно нулю.
Определение. Векторы  n -мерного евклидова пространства Rn образуют ортонормированный базис, если они попарно ортогональны, и норма каждого из них равна единице.
n -мерного евклидова пространства Rn образуют ортонормированный базис, если они попарно ортогональны, и норма каждого из них равна единице.
Существует теорема, устанавливающая одно из основных свойств евклидова пространства.
| Во всяком n -мерном евклидовом пространстве существует ортонормированный базис.
|
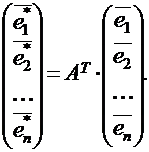
Примером одного из таких ортонормированных базисов является система из n единичных векторов, у которых i -ая компонента равна 1, а все остальные компоненты равны нулю, т.е. базис из векторов:  и т.д.
и т.д.
Линейные операторы
Если задан закон (правило), по которому каждому вектору  пространства Rn ставится в соответствие единственный вектор
пространства Rn ставится в соответствие единственный вектор 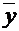 этого же пространства, то говорят, что задан оператор (преобразование, отображение)
этого же пространства, то говорят, что задан оператор (преобразование, отображение)  и записывают
и записывают  .
.
Оператор  называется линейным, если для любых векторов
называется линейным, если для любых векторов  и
и 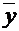 пространства Rn и любого действительного числа λ выполняются соотношения:
пространства Rn и любого действительного числа λ выполняются соотношения:
·  - свойство аддитивности оператора;
- свойство аддитивности оператора;
·  - свойство однородности оператора.
- свойство однородности оператора.
Опираясь на свойства линейности оператора, можно показать, что его воздействие на вектор  состоит в том, что матрица-столбец координат этого вектора (в некотором базисе) умножается слева на квадратную матрицу А оператора и в результате получается матрица-столбец координат вектора
состоит в том, что матрица-столбец координат этого вектора (в некотором базисе) умножается слева на квадратную матрицу А оператора и в результате получается матрица-столбец координат вектора 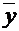 (в том же базисе), т.е. Y = AX. Другими словами, каждому линейному оператору можно поставить в соответствие единственную квадратную матрицу этого оператора.
(в том же базисе), т.е. Y = AX. Другими словами, каждому линейному оператору можно поставить в соответствие единственную квадратную матрицу этого оператора.
При переходе к другому базису в пространстве Rn матрица линейного оператора изменится. Можно показать, что матрицы А* и А линейного оператора  в новом базисе
в новом базисе  и в старом базисе
и в старом базисе  , соответственно, связаны соотношением:
, соответственно, связаны соотношением:  , где С – матрица перехода от старого базиса к новому (см. подраздел 3.4).
, где С – матрица перехода от старого базиса к новому (см. подраздел 3.4).
Определение. Ненулевой вектор  называется собственным вектором линейного оператора
называется собственным вектором линейного оператора  (или линейного преобразования, заданного матрицей А), если существует такое число λ, что справедливо равенство:
(или линейного преобразования, заданного матрицей А), если существует такое число λ, что справедливо равенство:  . При этом число λ называется собственным значением оператора
. При этом число λ называется собственным значением оператора  (или матрицы А), соответствующим собственному вектору
(или матрицы А), соответствующим собственному вектору  .
.
Из приведенного определения следует, что собственный вектор под воздействием линейного оператора переходит в вектор, коллинеарный самому себе, т.е. просто умножается на число – собственное значение, ему соответствующее.
Характеристическим уравнением матрицы А линейного оператора называется уравнение:
 . .
|
где λ – неизвестное собственное значение, Е – единичная матрица.
ПРИМЕР: Для матрицы

характеристическое уравнение будет иметь вид:

Таким образом, задача отыскания собственных векторов и собственных значений линейного оператора решается в следующей последовательности. Вначале составляют и решают характеристическое уравнение. Его решениями будут собственные значения, причем их количество не превосходит n. После этого, подставляя последовательно каждое из найденных собственных значений в систему однородных уравнений вида:

каждый раз решают ее методом Гаусса и выясняют структуру нетривиальных решений – координат собственного вектора, соответствующего данному собственному значению.
ПРИМЕР: Найдите собственные векторы линейного оператора, заданного матрицей:

Составим характеристическое уравнение для отыскания собственных значений:
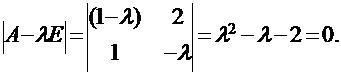
Решениями этого уравнения будут два собственных значения преобразования А: λ1 = 2 и λ2 = − 1.
Приступим к отысканию собственного вектора, соответствующего первому из собственных значений. Для этого запишем систему однородных уравнений:

Полученная система фактически представляет собой одно уравнение с двумя неизвестными. Положим 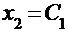 и найдем
и найдем 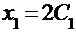 . Таким образом, собственный вектор, соответствующий первому из собственных значений, будет иметь следующие координаты:
. Таким образом, собственный вектор, соответствующий первому из собственных значений, будет иметь следующие координаты:
 ,
,
где С1 – любое действительное число, отличное от нуля.
Для второго собственного значения система однородных уравнений запишется в виде:

Т.е. представляет собой одно уравнение с двумя неизвестными. Полагая  , найдем
, найдем  , и окончательно запишем:
, и окончательно запишем:
 ,
,
где С2 – любое действительное число, отличное от нуля.
Критерий Сильвестра
| Для того чтобы квадратичная форма L = XTAX была положительно определенной, необходимо и достаточно, чтобы все главные миноры матрицы А этой формы были положительны.
|
В критерии Сильвестра под главными минорами матрицы понимают миноры i – го порядка, построенные следующим образом:

ПРИМЕР: Покажите положительную определенность квадратичной формы:  .
.
Найдем вначале матрицу этой формы. Поскольку эту форму можно переписать в виде: 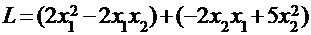 , искомая матрица имеет вид:
, искомая матрица имеет вид:

Характеристическое уравнение для этой матрицы будет иметь вид:
 , или:
, или:  .
.
Решая его, найдем:  , следовательно, на основании первого критерия можно заключить, что данная квадратичная форма является положительно определенной.
, следовательно, на основании первого критерия можно заключить, что данная квадратичная форма является положительно определенной.
Теперь найдем главные миноры матрицы А:
 .
.
Поскольку оба полученных минора положительны, на основании критерия Сильвестра заключаем, что данная квадратичная форма является положительно определенной.
Рекомендуемая литература по Теме 3: [1 ÷ 3].
ВОПРОСЫ для самопроверке знаний по теме 3:
1. При каком значении с векторы 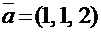 и
и 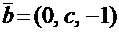 будут перпендикулярны?
будут перпендикулярны?
2. Сколько векторов будет содержать базис пространства  ?
?
3. Можно ли образовать ортонормированный базис из двух векторов:  ?
?
4. В какие векторы преобразует векторы (1, 0) и (0, 1) линейный оператор, заданный матрицей  ?
?
5. Является ли число 1 собственным значением матрицы  ?
?
6. Будет ли положительно определенной квадратичная форма  ?
?
Уравнения плоскости
Пусть заданы: прямоугольная система координат Oxyz; произвольная плоскость p; точка  , лежащая на плоскости p; а также вектор
, лежащая на плоскости p; а также вектор  , перпендикулярный плоскости p (рис. 4.1).
, перпендикулярный плоскости p (рис. 4.1).

Рис. 4.1.
Рассмотрим на плоскости p произвольную точку 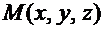 . Очевидно, что эта точка будет лежать на плоскости p тогда и только тогда, когда векторы
. Очевидно, что эта точка будет лежать на плоскости p тогда и только тогда, когда векторы  и
и  будут взаимно перпендикулярны (ортогональны), т.е. когда их скалярное произведение будет равно нулю. Поскольку:
будут взаимно перпендикулярны (ортогональны), т.е. когда их скалярное произведение будет равно нулю. Поскольку:
 и
и  ,
,
это условие можно записать в виде:
Это уравнение и есть уравнение плоскости, проходящей через точку М0 перпендикулярно вектору  .
.
Если в последнем уравнении раскрыть скобки и ввести обозначение: 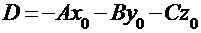 , то получим общее уравнение плоскости:
, то получим общее уравнение плоскости:
При этом вектор  , перпендикулярный плоскости p, называется нормальным вектором (или вектором нормали) этой плоскости.
, перпендикулярный плоскости p, называется нормальным вектором (или вектором нормали) этой плоскости.
Очевидно, что угол j между плоскостями, заданными общими уравнениями:
 и
и 
будет определяться углом j между нормальными векторами:  и
и  этих плоскостей, а косинус этого угла может быть найден по формуле:
этих плоскостей, а косинус этого угла может быть найден по формуле:
Условие параллельности рассматриваемых плоскостей эквивалентно условию коллинеарности нормальных векторов этих плоскостей, т.е. может быть записано в виде:
В свою очередь, условие перпендикулярности плоскостей вытекает из условия перпендикулярности нормальных векторов, т.е. из равенства нулю их скалярного произведения, и может быть записано в виде:
ЛИТЕРАТУРА
1. Налимов В.Н. Основы линейной алгебры для экономистов и менеджеров: Учебное пособие. – М.: Издание ИМЭС, 2013.
2. Ильин В.А., Ким Г.Д. Линейная алгебра и аналитическая геометрия: Учебник. – М.: Проспект, 2012.
3. Малугин В.А. Математика для экономистов. Линейная алгебра: Курс лекций. – М.: Эксмо, 2006.
ТЕОРЕТИКО – ПРАКТИЧЕСКИЙ КУРС
«ОСНОВЫ ЛИНЕЙНОЙ АЛГЕБРЫ



 .
.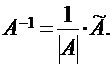












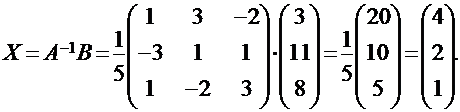







 и «новый»
и «новый»  . Очевидно, что каждый из векторов нового базиса можно представить в виде линейной комбинации векторов старого базиса:
. Очевидно, что каждый из векторов нового базиса можно представить в виде линейной комбинации векторов старого базиса: (*)
(*)
 имеет координаты
имеет координаты  относительно старого базиса и координаты
относительно старого базиса и координаты  относительно нового базиса, т.е. можно записать:
относительно нового базиса, т.е. можно записать:
 из равенств (*), то после несложных преобразований можно получить:
из равенств (*), то после несложных преобразований можно получить: (**)
(**) в новом базисе
в новом базисе  примера подраздела 3.3.
примера подраздела 3.3.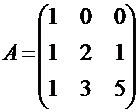 .
.
 в новом базисе
в новом базисе 

 и
и  называется число, равное:
называется число, равное:
 - коммутативное свойство;
- коммутативное свойство; - дистрибутивное свойство;
- дистрибутивное свойство; - свойство справедливое для любого действительного α;
- свойство справедливое для любого действительного α; , если
, если  , и
, и  , если
, если  .
.
 и носит название неравенства Коши-Буняковского.
и носит название неравенства Коши-Буняковского. можно определить равенством, непосредственно вытекающим из неравенства Коши-Буняковского:
можно определить равенством, непосредственно вытекающим из неравенства Коши-Буняковского: , где:
, где: 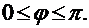
 и т.д.
и т.д. .
. - свойство аддитивности оператора;
- свойство аддитивности оператора; - свойство однородности оператора.
- свойство однородности оператора. , где С – матрица перехода от старого базиса к новому (см. подраздел 3.4).
, где С – матрица перехода от старого базиса к новому (см. подраздел 3.4). . При этом число λ называется собственным значением оператора
. При этом число λ называется собственным значением оператора  .
.




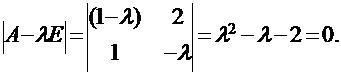

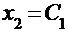 и найдем
и найдем 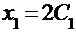 . Таким образом, собственный вектор, соответствующий первому из собственных значений, будет иметь следующие координаты:
. Таким образом, собственный вектор, соответствующий первому из собственных значений, будет иметь следующие координаты: ,
,
 , найдем
, найдем  , и окончательно запишем:
, и окончательно запишем: ,
,
 .
.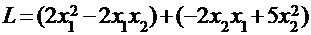 , искомая матрица имеет вид:
, искомая матрица имеет вид:
 , или:
, или:  .
. , следовательно, на основании первого критерия можно заключить, что данная квадратичная форма является положительно определенной.
, следовательно, на основании первого критерия можно заключить, что данная квадратичная форма является положительно определенной. .
.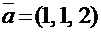 и
и 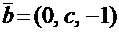 будут перпендикулярны?
будут перпендикулярны? ?
? ?
? ?
? ?
? ?
? , лежащая на плоскости p; а также вектор
, лежащая на плоскости p; а также вектор  , перпендикулярный плоскости p (рис. 4.1).
, перпендикулярный плоскости p (рис. 4.1).
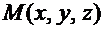 . Очевидно, что эта точка будет лежать на плоскости p тогда и только тогда, когда векторы
. Очевидно, что эта точка будет лежать на плоскости p тогда и только тогда, когда векторы  и
и  будут взаимно перпендикулярны (ортогональны), т.е. когда их скалярное произведение будет равно нулю. Поскольку:
будут взаимно перпендикулярны (ортогональны), т.е. когда их скалярное произведение будет равно нулю. Поскольку: и
и 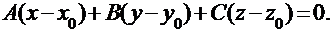
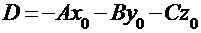 , то получим общее уравнение плоскости:
, то получим общее уравнение плоскости:
 и
и 
 и
и  этих плоскостей, а косинус этого угла может быть найден по формуле:
этих плоскостей, а косинус этого угла может быть найден по формуле: