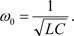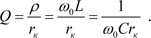Колебательный контурназывается идеальным, если он состоит из катушки и емкости и в нем нет сопротивления потерь.

Рассмотрим физические процессы в следующей цепи:
1 Ключ стоит в положении 1 Конденсатор начинает заряжаться, от источника напряжения и в нем накапливается энергия электрического поля,  т.е.конденсатор становится источником электрической энергии.
т.е.конденсатор становится источником электрической энергии.
2. Ключ в положении 2. Конденсатор начнет разряжаться. Электрическая энергия, запасенная в конденсаторе переходит в энергию магнитного поля катушки.

Ток в цепи достигает максимального значения(точка 1).
Напряжение на обкладках конденсатора уменьшается до нуля.
 В период от точки 1 до точки 2 ток в контуре уменьшается до нуля, но как только он начинает уменьшатся, то уменьшается магнитное поле катушки и в катушке индуцируется ЭДС самоиндукции, который противодействует уменьшению тока, поэтому он уменьшается до нуля не скачкообразно, а плавно. Так как возникает ЭДС самоиндукции, то катушка становится источником энергии. От этой ЭДС конденсатор начинает заряжаться, но с обратной полярностью (напряжение конденсатора отрицательное) (в точке 2 конденсатор вновь заряжается).
В период от точки 1 до точки 2 ток в контуре уменьшается до нуля, но как только он начинает уменьшатся, то уменьшается магнитное поле катушки и в катушке индуцируется ЭДС самоиндукции, который противодействует уменьшению тока, поэтому он уменьшается до нуля не скачкообразно, а плавно. Так как возникает ЭДС самоиндукции, то катушка становится источником энергии. От этой ЭДС конденсатор начинает заряжаться, но с обратной полярностью (напряжение конденсатора отрицательное) (в точке 2 конденсатор вновь заряжается).
Вывод: в цепи LC происходит непрерывное колебание энергии между электрическим и магнитным полями, поэтому такая цепь называется колебательным контуром.
Получившиеся колебания называются свободными или собственными, поскольку они происходят без помощи постороннего источника электрической энергии, внесенной ранее в контур (в электрическое поле конденсатора). Так как емкость и индуктивность идеальны (нет сопротивления потерь) и энергия из цепи не уходит, амплитуда колебаний с течением времени не меняется и колебания будут незатухающими.
Определим угловую частоту свободных колебаний:
Используем равенство энергий электрического и магнитного полей
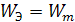
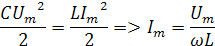


где ώ угловая частота свободных колебаний.
[ ώ ]=1/с
f0=ώ/2π [Гц].
Период свободных колебаний Т0=1/f.
Частоту свободных колебаний называют частотой собственных колебаний контура.
Из выражения: ώІLC=1 получим
ώL=1/Cώ, следовательно, при токе в контуре с частотой свободных колебаний индуктивное сопротивление равно емкостному сопротивлению.

 - характеристические сопротивления.
- характеристические сопротивления.
Индуктивное или емкостное сопротивление в колебательном контуре при частоте свободных колебаний называется характеристическим сопротивлением.
| СВОБОДНЫЕ КОЛЕБАНИЯ В КОНТУРЕ
| |
| Рассмотрим процессы, происходящие в цепи, составленной из конденсатора и катушки индуктивности (рис. 2-29), в которых не происходит потери энергии. Разомкнув ключ K, замкнем ключ K1, и зарядим конденсатор от источника постоянного тока. Затем разомкнем ключ K1 и замкнем ключ K. Конденсатор начнет разряжаться через катушку. Поскольку до этого в катушке тока не было, то вследствие действия э.д.с. самоиндукции ток iк увеличивается постепенно от нулевого значения, а напряжение на конденсаторе uC уменьшается. При этом запас энергии электрического поля конденсатора уменьшается, а запас энергии магнитного поля катушки увеличивается.
|

| | Рис. 2-29.
| Свободные колебания в контуре.
| |
| Когда напряжение на конденсаторе упадет до нуля, вся энергия электрического поля конденсатора перейдет в энергию магнитного поля катушки, которая достигнет максимума. Одновременно ток, проходящий через катушку, также достигнет максимального значения. Так как ток через катушку не может прекратиться скачком, то он спадает постепенно, перезаряжая при этом конденсатор, т.е. заряжая его пластины зарядами противоположного знака по сравнению с теми, которые были на них до эгого. Когда же ток спадет до нуля, вся энергия магнитного поля катушки перейдет в энергию электрического поля конденсатора и напряжение на конденсаторе станет таким же, каким оно было в начале процесса, но с обратным знаком. Затем процесс повторится, но разряд уже будет проходить в противоположном направлении.
Таким образом, в цепи происходят незатухающие электрические колебания с поочередным переходом энергии электрического поля конденсатора в энергию магнитного поля катушки и обратно. Поэтому такую цепь, состоящую из конденсатора и катушки индуктивности, называют колебательным контуром. Так как потерь в идеальном контуре нет, то этот процесс продолжается бесконечно. Аналогичные явления можно наблюдать в механических колебательных системах, например при колебаниях идеального маятника, в котором его потенциальная энергия в верхнем положении переходит в кинетическую энергию при нижнем положении (и обратно).
Рассмотренный процесс колебаний в контуре носит название свободных колебаний, так как он протекает без влияния внешней возбуждающей силы только благодаря наличию некоторого запаса энергии в одном из элементов цепи. Ток и напряжение в контуре, как видно из рис. 2-29, изменяются по синусоидальному закону, но со сдвигом по фазе на 90°.
Из равенства максимальных энергий конденсатора и катушки
|
|
| где
|
| UmC - амплитуда напряжения на конденсаторе, ImL - амплитуда тока в катушке, C - емкость конденсатора и L - индуктивность катушки,
|
| следует:
|
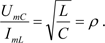
| (2-35)
| |
| Эта величина называется характеристическим сопротивлением контура и представляет собой сопротивление катушки или конденсатора для тока, проходящего через них (поскольку напряжения на них равны и через них проходит один и тот же ток, то и сопротивления их также равны):
|

| (2-36)
| |
| Раз при свободных колебаниях сопротивления конденсатора и катушки равны, то в контуре может проходить ток только определенной частоты, при которой
|

| (2-37)
| |
где  - круговая частота свободных, или, как их называют, собственных, колебаний контура.
Из этого выражения получаем формулу для определения круговой частоты собственных колебаний контура - круговая частота свободных, или, как их называют, собственных, колебаний контура.
Из этого выражения получаем формулу для определения круговой частоты собственных колебаний контура
|
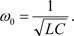
| (2-38)
| |
Здесь  - в радианах в секунду, L - в генри и C -в фарадах.
Частота собственных колебаний (в герцах) контура может быть найдена по формуле - в радианах в секунду, L - в генри и C -в фарадах.
Частота собственных колебаний (в герцах) контура может быть найдена по формуле
|

| (2-39)
| |
| Период колебаний в контуре
|

| (2-40)
| |
| Увеличение периода колебаний с увеличением индуктивности и емкости контура объясняется тем, что чем больше индуктивность контура, тем медленнее происходит изменение тока, и чем больше емкость, тем больше времени требуется на перезарядку конденсатора.
Мы рассматривали процесс колебаний в контуре без потерь. Однако в реальных контурах всегда происходят необратимые потери энергии на нагрев проводов и диэлектрика, а также на излучение, что приводит к постепенному уменьшению амплитуды электрических колебаний, или, как говорят, к их затуханию (рис. 2-30). При расчете контура полагают, что он имеет сосредоточенное сопротивление rк, потребляющее то же количество энергии, какое расходуется в контуре на все виды потерь.
|

| | | Затухающие колебания.
| |
| Колебания в контуре затухают тем быстрее, чем большая доля первоначально запасенной в контуре энергии теряется за период колебаний, т.е. чем больше сопротивление потерь по сравнению с его характеристическим сопротивлением. Отношение характеристического сопротивления контура к сопротивлению потерь называется добротностью Q контура:
|
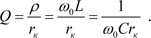
| (2-41)
| |
| Чем больше добротность, тем медленнее затухают свободные колебания в контурах с одинаковой частотой собственных колебаний. Используемые в радиотехнике контуры обычно имеют добротность от 50 до 300.
|






 т.е.конденсатор становится источником электрической энергии.
т.е.конденсатор становится источником электрической энергии.
 В период от точки 1 до точки 2 ток в контуре уменьшается до нуля, но как только он начинает уменьшатся, то уменьшается магнитное поле катушки и в катушке индуцируется ЭДС самоиндукции, который противодействует уменьшению тока, поэтому он уменьшается до нуля не скачкообразно, а плавно. Так как возникает ЭДС самоиндукции, то катушка становится источником энергии. От этой ЭДС конденсатор начинает заряжаться, но с обратной полярностью (напряжение конденсатора отрицательное) (в точке 2 конденсатор вновь заряжается).
В период от точки 1 до точки 2 ток в контуре уменьшается до нуля, но как только он начинает уменьшатся, то уменьшается магнитное поле катушки и в катушке индуцируется ЭДС самоиндукции, который противодействует уменьшению тока, поэтому он уменьшается до нуля не скачкообразно, а плавно. Так как возникает ЭДС самоиндукции, то катушка становится источником энергии. От этой ЭДС конденсатор начинает заряжаться, но с обратной полярностью (напряжение конденсатора отрицательное) (в точке 2 конденсатор вновь заряжается).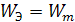
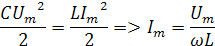



 - характеристические сопротивления.
- характеристические сопротивления.

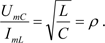


 - круговая частота свободных, или, как их называют, собственных, колебаний контура.
Из этого выражения получаем формулу для определения круговой частоты собственных колебаний контура
- круговая частота свободных, или, как их называют, собственных, колебаний контура.
Из этого выражения получаем формулу для определения круговой частоты собственных колебаний контура