Предмет механики. Системы отсчета. Траектория точки. Основные кинематические характеристики поступательного движения: радиус-вектор, перемещение, путь, скорость, ускорение.

Предмет механики. Системы отсчета. Траектория точки. Основные кинематические характеристики поступательного движения: радиус-вектор, перемещение, путь, скорость, ускорение.

Механика – это наука, изучающая механическое движение материальных объектов, то есть их взаимное перемещение в пространстве и во времени. Механика в свою очередь делится на три раздела: кинематика, динамика, статика.

Система отсчёта – совокупность системы координат и системы отсчета времени, по отношению к которым рассматривается движение каких-либо материальных точек.

Прежде чем решать любую задачу механики необходимо выбрать систему отсчёта.

Траектория – линия, вдоль которой двигается тело.

Основные кинематические характеристики поступательного движения:

1) Радиус-вектор – это вектор, ведущий из начала координат в эту точку. На плоскости углом радиус-вектора называется угол, на который радиус-вектор повёрнут относительно оси абсцисс в направлении против часовой стрелки.

2) Вектор перемещения -направленный отрезок, соединяющий начальную и конечную точки и указывающий направление движение.

3) Путь – длина участка траектории материальной точки, пройденного ею за определённое время.

4) Скорость - векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта

5) Ускорение -физическая величина, определяющая быстроту изменения скорости тела, то есть первая производная от скорости по времени.

 

Основные кинематические характеристики вращательного движения: угловой путь, угловая скорость, угловое ускорение.

Вращательное движение — вид механического движения. При вращательном движении абсолютно твёрдого тела его точки описывают окружности, расположенные в параллельных плоскостях. Центры всех окружностей лежат при этом на одной прямой, перпендикулярной к плоскостям окружности и называемой осью вращения. Ось вращения может располагаться внутри тела и за его пределами. Ось вращения может быть подвижной и неподвижной.

Пройденный путь, перемещение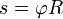

 

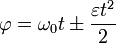
Угловой скоростью (мгновенной угловой скоростью) ω называется предел, к которому стремится средняя угловая скорость при бесконечном уменьшении промежутка времени ∆t, или первая производная от угла поворота по времени:

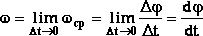
Угловое ускорение: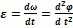

 

Работа при вращательном движении тела

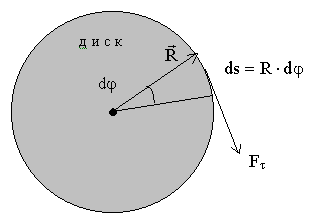
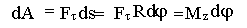
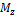- момент силы 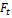относительно оси вращения z.

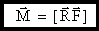- векторное произведение.

Кинетическая энергия при вращательном движении

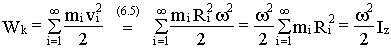
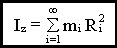
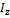- момент инерции твердого тела, относительно оси z.

Моментом инерции материальной точки называется величина:

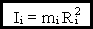
Следовательно,

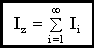
Величина I зависит от положения оси вращения и от распределения масс в теле.

Электрическое поле в проводниках и диэлектриках. Типы диэлектриков. Свободные и связанные заряды. Диэлектрическая проницаемость.

Магнитное поле

Опыт показывает, что, подобно тому, как в пространстве, окружающем электрические заряды, возникает электростатическое поле, так и в пространстве, окружающем токи и постоянные магниты, возникает силовое поле, называемое магнитным. Наличие магнитного поля обнаруживается по силовому действию на внесенные в него проводники с током или постоянные магниты. Название «магнитное поле» связывают с ориентацией магнитной стрелки под действием поля, создаваемого током (это явление впервые обнаружено датским физиком X. Эрстедом (1777—1851)).

Электрическое поле действует как на неподвижные, так и на движущиеся в нем электрические заряды. Важнейшая особенность магнитного поля состоит в том, что оно действует только на движущиеся в этом поле электрические заряды. Опыт показывает, что характер воздействия магнитного поля на ток различен в зависимости от формы проводника, по которому течет ток, от расположения проводника и от направления тока. Следовательно, чтобы охарактеризовать магнитное поле, надо рассмотреть его действие на определенный ток.

Подобно тому, как при исследовании электростатического поля использовались точечные заряды, при исследовании магнитного поля используется замкнутый плоский контур с током (рамка с током), линейные размеры которого малы по сравнению с расстоянием до токов, образующих магнитное поле. Ориентация контура в пространстве определяется направлением нормали к контуру. Направление нормали определяется правилом правого винта: за положительное направление нормали принимается направление поступательного движения винта, головка которого вращается в направлении тока, текущего в рамке.

Опыты показывают, что магнитное поле оказывает на рамку с током ориентирующее действие, поворачивая ее определенным образом. Этот результат используется для выбора направления магнитного поля. За направление магнитного поля в данной точке принимается направление, вдоль которого располагается положительная нормаль к рамке

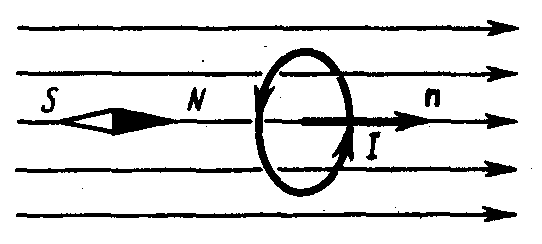
За направление магнитного поля может быть также принято направление, совпадающее с направлением силы, которая действует на северный полюс магнитной стрелки, помещенной в данную точку. Так как оба полюса магнитной стрелки лежат в близких точках поля, то силы, действующее на оба полюса, равны друг другу. Следовательно, на магнитную стрелку действует пара сил, поворачивающая ее так, чтобы ось стрелки, соединяющая южный полюс с северным, совпадала с направлением поля.

 

 

Вектор магнитной индукции и вектор напряженности магнитного поля.

Рамкой с током можно воспользоваться также и для количественного описания магнитного поля. Так как рамка с током испытывает ориентирующее действие поля, то на нее в магнитном поле действует пара сил. Вращающий момент сил зависит как от свойств поля в данной точке, так и от свойств рамки и определяется формулой

M = [p_mB] (109.1)

где p m — вектор магнитного момента рамки с током (В — вектор магнитной индукции, количественная характеристика магнитного поля). Для плоского контура с током I

p_m=ISn (109.2)

где S — площадь поверхности контура (рамки), n — единичный вектор нормали к поверхности рамки. Направление р m совпадает, таким образом, с направлением положительной нормали.

Если в данную точку магнитного поля помещать рамки с различными магнитными моментами, то на них действуют различные вращающие моменты, однако отношение М max /р m (М max — максимальный вращающий момент) для всех контуров одно и то же и поэтому может служить характеристикой магнитного поля, называемой магнитной индукцией:

B = M_max/p_m

Магнитная индукция в данной точке однородного магнитного поля определяется максимальным вращающим моментом, действующим на рамку с магнитным моментом, равным единице, когда нормаль к рамке перпендикулярна направлению поля. Следует отметить, что вектор В может быть выведен также из закона Ампера (с м. § 111) и из выражения для силы Лоренца (см. § 114).

Так как магнитное поле является силовым, то его, по аналогии с электрическим, изображают с помощью линий магнитной индукции — линий, касательные к которым в каждой точке совпадают с направлением вектора В. Их направление задается правилом правого винта: головка винта, ввинчиваемого по направлению тока, вращается в направлении линий магнитной индукции.

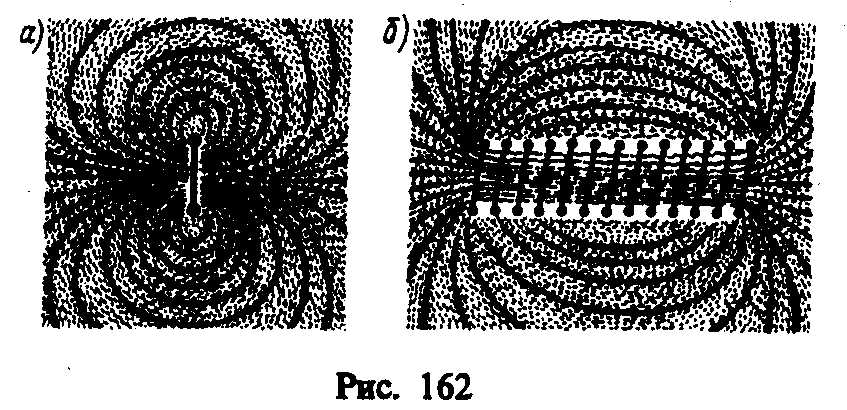Линии магнитной индукции можно «проявить» с помощью железных опилок, намагничивающихся в исследуемом поле и ведущих себя подобно маленьким магнитным стрелкам. На рис. 162, а показаны линии магнитной индукции поля кругового тока, на рис. 162, б — линии магнитной индукции поля соленоида (соленоид — равномерно намотанная на цилиндрическую поверхность проволочная спираль, по которой течет электрический ток).

Линии магнитной индукции всегда замкнуты и охватывают проводники с током. Этим они отличаются от линий напряженности электростатического поля, которые являются разомкнутыми (начинаются на положительных зарядах и кончаются на отрицательных (см. § 79)).

 

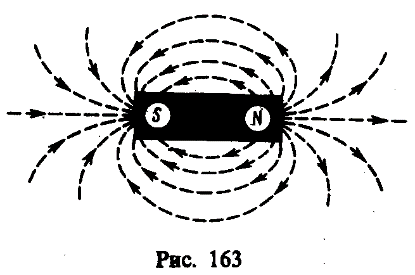
На ряс. 163 изображены линии магнитной индукции полосового магнита; они выходят из северного полюса и входят в южный. Вначале казалось, что здесь наблюдается полная аналогия с линиями напряженности электростатического поля и полюсы магнитов играют роль магнитных «зарядов» (магнитных монополей). Опыты показали, что, разрезая магнит на части, его полюсы разделять нельзя, т. е. в отличие от электрических зарядов свободные магнитные «заряды» не существуют, поэтому линии магнитной индукции не могут обрываться на полюсах. В дальнейшем было установлено, что внутри полосовых магнитов имеется магнитное поле, аналогичное полю внутри соленоида, и линии магнитной индукции этого магнитного поля являются продолжением линий магнитной индукции вне магнита. Таким образом, линии магнитной индукции магнитного поля постоянных магнитов являются также замкнутыми.

До сих пор мы рассматривали макроскопические токи, текущие в проводниках. Однако, согласно предположению французского физика А. Ампера (1775—1836), в любом теле существуют микроскопические токи, обусловленные движением электронов в атомах и молекулах. Эти микроскопические молекулярные токи создают свое магнитное поле и могут поворачиваться в магнитных полях макротоков. Например, если вблизи какого-то тела поместить проводник с током (макроток), то под действием его магнитного поля микротоки во всех атомах определенным образом ориентируются, создавая в теле дополнительное магнитное поле. Вектор магнитной индукции В характеризует результирующее магнитное поле, создаваемое всеми макро- и микротоками, т. е. при одном и том же токе и прочих равных условиях вектор В в различных средах будет иметь разные значения.

П09.3)

Магнитное поле макротоков описывается вектором напряженности Н. Для однородной изотропной среды вектор магнитной индукции связан с вектором напряженности следующим соотношением:

B = μ₀μH

где μ0 — магнитная постоянная, μ — безразмерная величина — магнитная проницаемость среды, показывающая, во сколько раз магнитное поле макротоков Н усаливается за счет поля микротоков среды.

Сравнивая векторные характеристики электростатического (Е и D) и магнитного (В и Н) полей, укажем, что аналогом вектора напряженности электростатического поля Е является вектор магнитной индукции В, так как векторы Е и В определяют силовые действия этих полей и зависят от свойств среды. Аналогом вектора электрического смещения D является вектор напряженности Н магнитного поля.

 

Закон Ампера.

Магнитное поле (см. § 109) оказывает на рамку с током ориентирующее действие. Следовательно, вращающий момент, испытываемый рамкой, есть результат действия сил на отдельные ее элементы. Обобщая результаты исследования действия магнитного поля на различные проводники с током. Ампер установил, что сила d F, с которой магнитное поле действует на элемент проводника d l с током, находящегося в магнитном поле, равна

dF = I[dl, B] (111.1)

где d l —вектор, по модулю равный d l и совпадающий по направлению с током, В — вектор магнитной индукции.

Направление вектора d F может быть найдено, согласно (111.1), по общим правилам векторного произведения, откуда следует правило левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы, действующей на ток.

Модуль силы Ампера (см. (111.1)) вычисляется по формуле

dF = IBdlsina (111.2)

где a — угол между векторами d l и В.

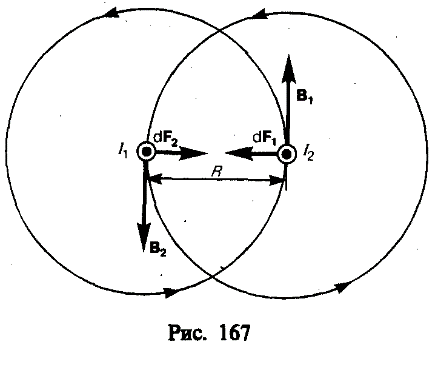Закон Ампера применяется для определения силы взаимодействия двух токов. Рассмотрим два бесконечных прямолинейных параллельных тока I 1 и I 2; (направления токов указаны на рис. 167), расстояние между которыми равно R. Каждый из проводников создает магнитное поле, которое действует по закону Ампера на другой проводник с током. Рассмотрим, с какой силой действует магнитное поле тока I 1 на элемент d l второго проводника с током I 2. Ток I 1 создает вокруг себя магнитное поле, линии магнитной индукции которого представляют собой концентрические окружности. Направление вектора B 1 определяется правилом правого винта, его модуль по формуле 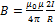(110.5) равен

 

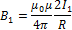
Направление силы d F 1, с которой поле B 1 действует на участок d l второго тока, определяется по правилу левой руки и указано на рисунке. Модуль силы, согласно (111.2), с учетом того, что угол  между элементами тока I 2 и вектором B 1 прямой, равен

dF₁ = I₂B₁dl

подставляя значение для В 1, получим

dF₁ = (111.3)

Рассуждая аналогично, можно показать, что сила d F 2 с которой магнитное поле тока I 2 действует на элемент d l первого проводника с током I 1, направлена в противоположную сторону и по модулю равна

dF₂ =I₁B₂dl = (111.4)

Сравнение выражений (111.3) и (111.4) показывает, что

dF₁ = dF₂

т. е. два параллельных тока одинакового направления притягиваются друг к другу с силой

dF = (111.5)

Если токи имеют противоположные направления, то, используя правило левой руки, можно показать, что между ними действует сила отталкивания, определяемая формулой (111.5).

 

Индуктивность соленоида.

Соленоид — длинная, тонкая катушка, то есть катушка, длина которой намного больше, чем её диаметр (также в дальнейших выкладках здесь подразумевается, что толщина обмотки намного меньше, чем диаметр катушки). При этих условиях и без использования магнитного материала плотность магнитного потока (или магнитная индукция) 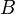, которая выражается в системе СИ в тесла [Тл], внутри катушки является фактически постоянной и (приближённо) равна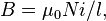

где 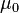− магнитная постоянная, 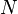− число витков, 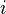− ток, записанный в амперах [А] и − длина катушки в метрах [м]. Пренебрегая краевыми эффектами на концах соленоида, получим^[16], что потокосцепление через катушку равно плотности потока 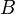[Тл], умноженному на площадь поперечного сечения 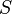[м²] и число витков :

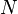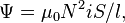
Отсюда следует формула для индуктивности соленоида (без сердечника):

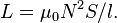
Если катушка внутри полностью заполнена магнитным материалом (сердечником), то индуктивность отличается на множитель 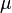— относительную магнитную проницаемость^[17] сердечника:

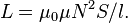
В случае, когда 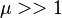, можно (следует) под S понимать площадь сечения сердечника [м²] и пользоваться данной формулой даже при толстой намотке, если только полная площадь сечения катушки не превосходит площади сечения сердечника во много раз.

Магнитное поле в веществе.

До сих пор рассматривалось магнитное поле, которое создавалось проводниками с током или движущимися электрическими зарядами, находящимися в вакууме. Если же магнитное поле создается не в вакууме, а в какой-то другой среде, то магнитное поле изменяется. Это объясняется тем, что различные вещества, помещенные в магнитное поле, намагничиваются и сами становятся источниками магнитного поля. Вещества, способные намагничиваться в магнитном поле, называются магнетиками. Намагниченное вещество создает магнитное поле с индукцией , которое накладывается на магнитное поле с индукцией , обусловленное токами. Оба поля в сумме дают результирующее поле, магнитная индукция которого равна

.

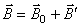Для объяснения намагничивания тел Ампер предположил, что в молекулах вещества циркулируют круговые токи. Каждый такой ток обладает магнитным моментом и создает в окружающем пространстве магнитное поле. В отсутствие внешнего магнитного поля молекулярные токи ориентированы хаотически, поэтому суммарный магнитный момент вещества равен нулю. В магнитном поле молекулярные токи ведут себя подобно рамке с током, то есть ориентируются так, чтобы магнитные моменты были преимущественно ориентированы вдоль магнитного поля, вследствие чего магнетик намагничивается. Природа молекулярных токов стала понятной только в начале ХХ в., когда Резерфордом было установлено, что атомы всех веществ состоят из положительно заряженного ядра и движущихся вокруг него отрицательно заряженных электронов. В 1913 г. Нильс Бор развил теорию, согласно которой электроны в атомах движутся по круговым орбитам. Это движение можно рассматривать как круговой ток, обладающий магнитным моментом, называемым орбитальным магнитным моментом электрона. Позднее было показано, что теория Бора имеет ограниченную применимость и во многих отношениях совершенно неверна. Тем не менее, согласно современным представлениям, электроны в атомах обладают орбитальным магнитным моментом. Кроме того, электрон имеет собственный магнитный момент, называемый спиновым магнитным моментом. Магнитный момент многоэлектронного атома будет векторной суммой орбитальных и спиновых моментов всех его электронов.

Именно взаимодействием магнитных моментов атомов с внешним магнитным полем и обусловлено намагничивание веществ и, следовательно, изменение магнитного поля в веществе. Для описания этого поля вводят величину m, которая называется относительной магнитной проницаемостью или просто магнитной проницаемостью вещества. Магнитная проницаемость 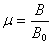показывает, во сколько раз значение магнитной индукции в веществе отличается от ее значения в вакууме при тех же значениях токов, создающих магнитное поле. Магнитная проницаемость зависит от рода вещества и от его состояния, например, от температуры.

Предмет механики. Системы отсчета. Траектория точки. Основные кинематические характеристики поступательного движения: радиус-вектор, перемещение, путь, скорость, ускорение.

Механика – это наука, изучающая механическое движение материальных объектов, то есть их взаимное перемещение в пространстве и во времени. Механика в свою очередь делится на три раздела: кинематика, динамика, статика.

Система отсчёта – совокупность системы координат и системы отсчета времени, по отношению к которым рассматривается движение каких-либо материальных точек.

Прежде чем решать любую задачу механики необходимо выбрать систему отсчёта.

Траектория – линия, вдоль которой двигается тело.

Основные кинематические характеристики поступательного движения:

1) Радиус-вектор – это вектор, ведущий из начала координат в эту точку. На плоскости углом радиус-вектора называется угол, на который радиус-вектор повёрнут относительно оси абсцисс в направлении против часовой стрелки.

2) Вектор перемещения -направленный отрезок, соединяющий начальную и конечную точки и указывающий направление движение.

3) Путь – длина участка траектории материальной точки, пройденного ею за определённое время.

4) Скорость - векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта

5) Ускорение -физическая величина, определяющая быстроту изменения скорости тела, то есть первая производная от скорости по времени.