Между частицами твердого ненагруженного тела действуют силы взаимодействия, обеспечивающие неизменность его геометрической формы. При действии внешних нагрузок силы взаимодействия изменяются и тело деформируется. Под внутренними силами понимается приращение сил взаимодействия между частицами, возникающее при его нагружении.
Понятие о напряжениях. Напряжение является количественной мерой интенсивности внутренних сил в точках деформируемого тела. Зафиксируем некоторую точку М в сечении тела с единичным вектором нормали n (рис. 4.1). В окрестности этой точки выделим площадку D F, на которой действует главный вектор внутренних сил D P. При уменьшении размеров площадки в пределе получаем
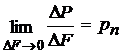 . (46)
. (46)
Вектор pn называется вектором напряжений в точке.Он зависит не только от действующих на тело внешних сил и координат точки М, но и от ориентации площадки D F, в пространстве, определяемой нормалью п. Совокупность всех векторов напряжений в точке М для всевозможных направлений вектора n определяет напряженное состояние в точке.
Проекция вектора рn на направление n называется нормальным напряжением s n, (рис. 4.2), а проекция на плоскость, проходящую через точку М и ортогональную вектору n, - касательным напряжением t n:
pn 2 = s n 2 + t n 2.(47)
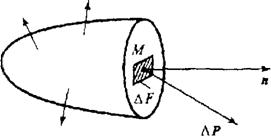
Рис. 4.1. Главный вектор внутренних сил на площадке D F

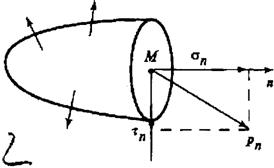
Рис. 4.2. Вектор напряжений рn, нормальное s n и касательное t n напряжения
в точке М
Напряжения на произвольно ориентированных площадках могут быть выражены черезэти три вектора напряжений. Разложим каждый вектор напряжений на составляющие вдоль координатных осей (рис. 4.3, 4.4).На каждой площадке действует одно нормальноенапряжение s x, s у, s z, где индекс обозначает направление вектора нормали к площадке, и два касательных напряжения tс двумя индексами, изкоторых первый указывает направление действия компоненты напряжения, второй - направление вектора нормали к площадке. Совокупность девяти компонент (по три на каждой из трех взаимно перпендикулярных площадок) представляет собой тензор напряжений в точке. Тензор напряжений обладает свойством симметрии: t xy = t yx; t xz = t zx; t yz = t zy. Эти условия называются также условиями парности (взаимности) касательных напряжений.


Рис. 4.3. Векторы напряжений на элементарных площадках

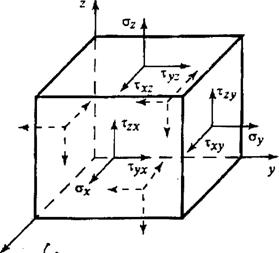
Рис. 4.4. Компоненты вектора напряжений
Размерность напряжений равна отношению размерности силы к размерности площади. В системе СИ напряжения измеряются в паскалях (1 Па = 1 Н/м2).
Понятие о деформациях. При действии внешних сил происходит изменение объема тела и его формы, т.е. тело деформируется. Различают начальное (недеформированное)и конечное (деформированное) состояния тела(рис. 4.5).Выделим в окрестности точки М элементарный параллелепипед с размерами dx dy dz (рис. 4.6). При деформировании длины его ребер получают абсолютные удлинения D dx, D dy, D dz. Относительные линейные деформации в точке М вводятся следующим образом:
 (48)
(48)
Относительные линейные деформаций (3) - величины безразмерные и для распространенных конструкционных материалов имеют порядок e = 10-3, т.е. достаточно малы. Кроме линейных деформаций возникают угловые деформации (углы сдвига) (рис. 4.6), определяемые как малые изменения первоначально прямых углов граней параллелепипеда. Как и линейные деформации, углы сдвига малы и имеют порядок g 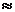 10-4.
10-4.
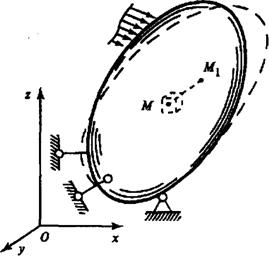
Рис. 4.5. Полное перемещение точки и его компоненты


Рис. 4.6. Линейная и угловая деформации элемента





 . (46)
. (46)






 (48)
(48) 10-4.
10-4.





