

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
Топ:
Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного...
Процедура выполнения команд. Рабочий цикл процессора: Функционирование процессора в основном состоит из повторяющихся рабочих циклов, каждый из которых соответствует...
Характеристика АТП и сварочно-жестяницкого участка: Транспорт в настоящее время является одной из важнейших отраслей народного...
Интересное:
Что нужно делать при лейкемии: Прежде всего, необходимо выяснить, не страдаете ли вы каким-либо душевным недугом...
Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны...
Распространение рака на другие отдаленные от желудка органы: Характерных симптомов рака желудка не существует. Выраженные симптомы появляются, когда опухоль...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Плотностью распределения вероятностей (или дифференциальной функцией распределения) непрерывной случайной величины Х называется функция f(x), задаваемая равенством f(x)=F’(x),  .
.
График функции f(x) называется кривой распределения величины Х.
Свойства:
1)  ;
;
2)  ;
;
3) Теорема о вероятности попадания в заданный интервал.
Х – непрерывная случайная величина, f(x) – плотность распределения, 

4)  условие нормировки;
условие нормировки;
5) геометрически вероятность попадания случайной величины Х в промежуток (a;b) равна площади соответствующей криволинейной трапеции, ограниченной кривой распределения, осью Ох и прямыми x=a, x=b.
6) Если все значения случайной величины Х заключены в промежутке (a1;a2), то 
12. Пусть имеется случайная величина Х с математическим ожиданием mx.
Центрированной случайной величиной, соответствующей величине Х, называется отклонение случайной величины Х от её математического ожидания. Центрирование случайной величины равносильно переносу начала координат в точку, абсцисса которой равна математическому ожиданию.
Мат ожид приближенно = среднему знач случ величины. Математическим ожиданием дискретной случайной величины называют сумму произведений всех ее возможных значений на их вероятности.
M(Х)=интеграл от i=1 до бескон хipi
Если дискретная случайная величина X принимает счетное множество возможных значений, то математическое ожидание существует, если ряд в правой части равенства сходится абсолютно.
Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а,Ь], называют определенный интеграл
ь М(Х)=интегрxf(x)dx
а
Если возможные значения принадлежат всей оси Ох, то
|
|
M(X)=интегр от – беск до +беск xf (x)dx.
Предполагается, что несобственный интеграл сходится абсолютно Свойства математического ожидания.
1. Математическое ожидание постоянной величины равно самой
постоянной.
М(С) = С.
2. Постоянный множитель можно выносить за знак математического
ожидания. М(СХ)=СМ(Х).
3. Математическое ожидание произведения двух независимых случайных
величин равно произведению их математических ожиданий.
X xi x2 Y yi у2
Р Pi Рг g gi g2
Составим все значения, которые может принимать случайная величина XY
XY xiy, х,у2 x2yi х2у2
Р Plgl Plg2 P2gl P2g2
Математическое ожидание равно сумме произведений всех возможных
значений на их вероятности:
M(XY) = Xiyip^i + x2yip2qi + X!y2piq2 + х2у2р2Ч2 = - yi4i(xiPi + х2р2) + УгчгСхф! + хгр2) = (x,pi + x2p2)(yiq, + y2q2) = = M(X) + M(Y).
Мат ожид суммы двух случ величин = сумме мат ожид слагаемых. М(Х+Y)=М(Х)+М(Y)
13. Дисперсия случайной величины, ее свойства. Среднеквадратичное отклонение.
Дисперсией случайной величины X называется математическое ожидание квадрата отклонения случайно величины Х от ее математического ожидания: D(X)=M(X-M(X))2.
Свойства: 1) D[C]=0, где C=const.дисп пост вел С =0
2) D[CX]=C в квадрате на D[X]-постоянный множитель можно выносить за знак дисперсии,возведя его в квадрат
3) X,Y независимы, D[X+(-)Y]=D[X]+D[Y]
4) D[X+C]=D[X]
Для оценки рассеяния возможных значений случ вел вокруг ее среднего значения кроме дисперсии служат и некоторые другие характеристики.к их числу относят и среднекв отклон.
Среднеквадратическим отклонение случайной величины Х называется число, вычисляемое по формуле 
Легко показать,что дисперсия имеет размерность,равную квадрату размерности случ аеличины.Т.к. среднекв отклон = квадратному корню из дисперсии,то размерность сигма(Х) совпадает с размерностью Х.Поэтому в тех случаях,когда желательно,чтобы оценка рассеяния имела размерность случ велич,вычисляют среднекв отклон,а не дисперсию.
Моме́нт случа́йной величины́ — числовая характеристика распределения данной случайной величины
|
|
Если дана случайная величина  определённая на некотором вероятностном пространстве, то:
определённая на некотором вероятностном пространстве, то:

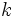 -м нача́льным моментом случайной величины
-м нача́льным моментом случайной величины  где
где  называется величина
называется величина
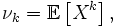
если математическое ожидание  в правой части этого равенства определено;
в правой части этого равенства определено;
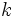 -м центра́льным моментом случайной величины
-м центра́льным моментом случайной величины  называется величина
называется величина

если математическое ожидание в правой части этого равенства определено. Если определены моменты 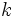 -го порядка, то определены и все моменты низших порядков
-го порядка, то определены и все моменты низших порядков  В силу линейности математического ожидания центральные моменты могут быть выражены через начальные, и наоборот. Например:
В силу линейности математического ожидания центральные моменты могут быть выражены через начальные, и наоборот. Например:

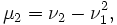

|
|
|

История развития пистолетов-пулеметов: Предпосылкой для возникновения пистолетов-пулеметов послужила давняя тенденция тяготения винтовок...

Типы оградительных сооружений в морском порту: По расположению оградительных сооружений в плане различают волноломы, обе оконечности...

Двойное оплодотворение у цветковых растений: Оплодотворение - это процесс слияния мужской и женской половых клеток с образованием зиготы...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!