Импульс силы. Количество движения

3.3.1. Постоянная по модулю и направлению сила действует на тело в течение 10 с. Найти модуль ее импульса за это время, если проекции силы на оси координат F_x = 3 Н, F_y = 4 Н. (50)

3.3.2. Модуль постоянной по направлению силы изменяется по закону F = 5 + 9 t ². Найти модуль импульса этой силы за промежуток вре­мени τ = t ₂ –t ₁, где t ₂ = 2 с, t ₁= 0. (34)

3.3.3. На материальную точку М действует сила . Опреде­лить проекцию импульса силы на ось Ох за промежуток времени τ = t ₂ –t ₁, где t ₂ = 2c, t ₁= 0. (8)

3.3.4. Материальная точка массой т = 1 кг движется по прямой с посто­янным ускорением a = 5 м/с². Определить импульс равнодействую­щей приложенных к точке сил за промежуток времени τ = t ₂ –t ₁, где t ₂ = 4c, t ₁ = 2 c.(10)

3.3.5. Модуль постоянной по направлению силы изменяется по закону, показанному на рисун­ке 403. Определить модуль импульса этой силызапромежуток времени τ = t ₂ –t ₁, где t ₂= 5 с, t ₁ = 0.(18)

3.3.6. Материальная точка массой т = 1 кг (рис. 404) дви­жется по закону s = 2 + 0,5 е ^{2 t}. Определить модуль количества движения точки в момент времени t = 1 с. (7,39)

 

Рис. 403 Рис. 404 Рис. 405

3.3.7. Шкив 1 (рис. 405) радиуса R = 0,4 м, вращаясь с уг­ловой скоростью ω = 2,5 рад/с, поднимает груз 2 массой т = 10 кг. Определить модуль количества движения груза. (10)

3.3.8. Материальная точка массой т = 0,5 кг движется согласно век­торному уравнению . Определить проекцию количества движения точки на ось Ох в момент времени t = 0,5 с. (0)

3.3.9. Материальная точка массой 2 кг движется в плоскости Оху со­гласно уравнениям х = sin πt, у = 0,5 t ². Определить модуль количе­ства движения точки в момент времени t = 1,5 с. (3)

3.3.10. Материальная точка М массой 0,5 кг дви­жется по окружности радиуса R = 2 м (рис.406). Опреде­лить количество движения этой точки в момент времени t = π с, если угол φ = 5 sin 2 t. (10)

3.3.11. Трубка (рис. 407) вращается с угловой скоростью ω = 10 рад/с. Относительно трубки движется шарик М массой т = 0,2 кг со скоростью v_r = 4 м/с. Определить модуль количества движения шарика в момент времени, когда расстояние ОМ = 0,4 м. (1,13)

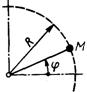
Рис. 406 Рис. 407 Рис. 408

3.3.12. Диск радиуса R = 0,4 м (рис.408) вращается с угло­вой скоростью ω = 25 рад/с. По ободу диска движется точка М согласно закону s = 1 + 2 t ². Определить модуль количества движения этой точки в момент времени t = 1 с, если ее масса т = 1 кг.(18)

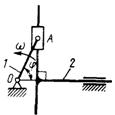
Рис. 409 Рис. 410 Рис. 411

3.3.13. Определить модуль количества движения ползуна 2 (рис.409), масса которого т ₂ = 1 кг, в мо­мент времени, когда угол α = 60°, если ползун 1 движется со скоростью v = 2 м/с. (1,15)

3.3.14. Кривошип 1 длиной ОА = 0,25 м (рис.410), враща­ясь с угловой скоростью ω = 10 рад/с, приво­дит в движение кулису 2 массой 6 кг. Опреде­лить модуль количества движения кулисы в момент времени, когда угол φ = 60°. (13,0)

3.3.15. Однородный стержень массой т = 10 кг и длиной l = 1 м (рис. 411) вращается по закону φ = 5 t ². Определить модуль количества движения это­го стержня в момент времени t = 2 с. (100)

3.3.16. Однородная прямоугольная пластина (рис. 412) мас­сой т = 12 кг вращается с угловой скоростью ω = 10 рад/с. Определить модуль количества движения пластины, если размеры l ₁ = 0,6 м, l ₂ = 0,8 м. (60)

Рис. 412 Рис. 413 Рис. 414

3.3.17. Центр масс колеса (рис. 413) движется по окружнос­тирадиуса R = 2 м согласно закону s = 5 sin 2 t. Определить модуль количества движения ко­леса в момент времени t = π с, если его масса равна 4 кг. (40)

3.3.18. Шкив 2 (рис. 414) радиуса R = 0,2 м, вращаясь с угловой скоростью ω = 20 рад/с, поднимает однородный цилиндр 1 массой т = 50 кг. Определить модуль количества движения цилиндра 1. (100)

Теорема об изменении количества движения

3.3.19*. Электромотор установлен на двухопорной балке, статиче­ский прогиб которой равен δ_ст = 5 см (рис. 415). Масса ротора равна 18 кг, масса ротора - 14 кг. Центр тяжести ротора мотора смещен по отношению к оси вращения на r = 0,5 см, ротор вра­щается с угловой скоростью ω = 24 рад/с. Пренебрегая массой бал­ки, найти уравнение вынужденных колебаний мотора.

Oтвет: х = 0,43 sin (24 t + π) см.

Рис. 415 Рис. 416

3.3.20*. На платформе АВ, соединенной с неподвиж-ной стенкой по­средством пружины жесткостью с = 3920 Н/м, закреплен мотор (рис. 416), масса платформы и мотора равна 19 кг. На вал мото­ра на расстоянии l = 1 см от оси О вала насажен груз M массой 1 кг. Угловая скорость мотора ω = 14 рад/с. Найти вынужденные ко­лебания платформы

Ответ: х_вын = - 0,35 t cos14 t см.

3.3.21*. По пластине В массой т_B = 2 т, лежащей на гладкой горизон­тальной плоскоcти и закрепленной пружиной жесткостью с, движется груз А массой т_А = т (рис. 417); закон относительного движения груза s = at ². Определить закон движения пластины, если в начальный момент она находилась в покое и пружина была не напряжена

Ответ: х = , где k = .

3.3.22. Материальная точка массой 0,5 кг движется по прямой. Опреде­лить модуль импульса равнодействую-щей всех сил, действующих на точку за первые 2 с, если она движется по закону s = 4 t ³. (24)

3.3.23. На материальную точку массой 1 кг действует

сила постоянного направления (рис. 418), зна­чение которой изменяется по закону F = S cos vt. Определить скорость этой точки в момент времени t = 0,5 с, если начальная скорость точки v ₀ = 1,5 м/с. (3,09)

 

 

3.3.24. На материальную точку массой 2 кг дейст­вует сила постоянного направления (рис. 418), значение которой изменяется по закону F = 6 t². Опре­делить скорость этой точки в момент времени t = 2с, если начальная скорость точки v ₀ = 2м/с. (10)

Рис. 417 Рис. 418 Рис. 419

3.3.26. На материальную точку массой т = 4 кг действует сила . Определить проекцию на ось Оу скорости точки в момент времени t = 2 с, если движение начинается из состояния покоя. (0,5)

2.3.27. Материальная точка М массой 1 кг дви­жется по прямой (рис. 419) под действием постоянной силы 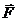. Скорость точки за промежуток време­ни τ = t ₂- t ₁, где t ₂ = 3 с, t ₁ = 0, изменилась от v ₀ = 2 м/с до v = 5 м/с. Определить модуль силы F. (1)

3.3.28. Количество движения материальной точки М (рис. 420) изменяется по закону . Опреде-лить проекцию на ось Оу равнодействующей сил, приложенных к точке. (12)

3.3.29. Материальная точка М движется по верти­кали (рис. 421) под действием только силы тяжести. Определить, через какое время эта точка дос­тигнет максимальной высоты, если ее началь­ная скорость v ₀ = 9,81 м/с. (1)

 

Рис. 420 Рис. 421 Рис. 422

3.3.30. Материальная точка М массой т = 1 кг (рис. 422) равномерно движется по окружности со ско­ростью v = 4 м/с. Определить модуль импульса равнодействую-щей всех сил, действующих на эту точку за время ее движения из положения 1 в положение 2. (5,66)

 

Рис. 423 Рис. 424

3.3.31. Материальная точка М массой т = 1 кг (рис. 433) равномерно движется по окружности радиуса R = 0,5 м со скоростью . Ускорение точки а = 8 м/с². Определить модуль импульса рав­нодействующей всех сил, действующих на эту точку за время ее движения из положения 1 в положение 2 (2,83)

3.3.32. Материальная точка массой 0,5 кг (рис. 434) движет­ся по окружности с постоянной скоростью v = 2 м/с. Найти проекцию на ось Ох импульса равнодействующей всех сил, действующих на точку, за время ее движенияиз положения А в положение В. (2)

3.3.33. Поезд движется по прямолинейному горизонтальному участку пути. При торможении развивается сила сопротивления, равная 0,2 веса поезда. Через какое время поезд остановится, если его начальная скорость 20 м/с. (20)

3.3.34. Модуль вектора количества движения механической системы изменяется по закону Q = 4 t ². Определить модуль главного вектора внешних сил, действующих на систему, в момент времени t = 2 c, если вектор количества движения и главный вектор внешних сил параллельны.(16)

 

3.4. ТЕОРЕМА ОБ ИЗМЕНЕНИИ КИНЕТИЧЕСКОГО МОМЕНТА

Моменты инерции

Осевые:

Центробежные:

Полярный .

.

Задачи

3.4.1. Определить момент инерции относительно плоскости Оху материальной точки массой 2 кг, если ее координаты х = 0,8 м, у = 0.6 м, z = 0,4 м. (0,32)

3.4.2. Определить момент инерции относительно плоскости Оху механической системы (рис. 425), состоя­щей из четырех одинаковых материальных точек, если масса каждой точки т = 1,5 кг, а радиус r = 0,4 м. (0,48)

3.4.3. Определить момент инерции относительно оси Оу механической системы (рис. 426), состоящей из трех одинаковых материальных точек, если радиус r = 0,6 м, а масса каждой точки т = 3кг. (1,62)

Рис. 425 Рис. 426 Рис. 427

3.4.4. Определить момент инерции относительно центральной оси Оу однородной тонкой квад­ратной пластины (рис. 427) массой т = 0,3 кг, имеющей отверстие радиуса r = 0,04 м. (4,89 ·10^-4)

3.4.5. Определить полярный момент инерции ме­ханической системы (рис. 428), состоящей из трех одина­ковых материальных точек, относительно нача­ла координат О, если расстояние l = 0,3 м, а масса каждой точки т = 0,5 кг. (0,27)

3.4.6. Определить момент инерции однородного диска (рис. 429) относительно центра О, если его момент инерции относительно оси Ох равен 3 кг·м². (6)

3.4.7. Определить центробежный момент инерции J_xy материальной точки массой 0,5 кг относительно осей Ох, Оу, если координаты точки х = 0,4 м, у = -0,5 м, z = 0,4 м. (-0,1)

 

Рис. 428 Рис. 429 Рис. 430

 

3.4.8. Определить центробежный момент инер­ции механической системы (рис. 430), состоящей из четы­рех

одинаковых материальных точек, относи­тельно осей Ох, Оу, если расстояния l ₁ = 0,4 м, l ₂ = 0,8 м, а масса каждой точки т = 2 кг. (0,64)

3.4.9. Определить центробежный момент инер­ции механической системы (рис. 431), состоящей из двух материальных точек, относительно осей Ох, Оу. Массы точек т ₁ = 1 кг, т ₂ = 2 кг, рассто­яние l = 0,5 м. (-0,325)

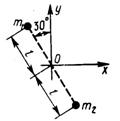
Рис. 431 Рис. 432 Рис. 433

3.4.10. Определить центробежный момент инер­ции J_xy однородного конуса (рис. 432) относительно осей Оу, Oz. (0)

3.4.11. Определить радиус инерции тела (рис. 433) массой т = 150 кг относительно оси Oz, если его момент инерции относительно этой оси равен 1,5 кг·м². (0,1)

Кинетический момент системы

Кинетическим моментом системы называют главный момент количества движения всех точек системы:

.

Кинетический момент твердого тела относительно неподвижной оси его вращения определяют формулой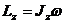

Задачи

3.4.12. Материальная точка массой т = 0,5 кг движется по оси Оу согласно уравнению у = 5 t ². Определить момент количества движения этой точки относительно центра О в момент времени t = 2 c. (0)

3.4.13. Материальная точка массой т = 1 кг движется по закону: х = 2 t, у = t ³, z = t ⁴. Определить момент количества движения этой точки относительно оси Оу в момент времени t = 2 с. (-96)

3.4.14. Скорость материальной точки массой т = 1кг определяется вы­ражением . Определить модуль момента количества движения точки относитель-но начала координат в момент времени t = 2 с, когда ее координаты х = 2м, у = 3 м, z = 3 м. (10,0)

3.4.15. Трубка (рис. 434) равномерно вращается с угловой скоростью ω = 10 рад/с. По трубке движется шарик массой m = 1 кг. Определить момент количества движения шарика относительно оси вращения трубки, когда расстояние ОМ = 0,5 м и скорость шарика относительно труб­ки v_r = 2 м/с. (2,5)

3.4.16. Конус (рис. 435) вращается равномерно вокруг оси Az с угловой скоростью ω = 4 рад/с. По обра­зующей конуса движется материальная точка М массой

1 кг. Определить момент количества движения материальной точки относительно оси Oz в положении, когда расстояние ОМ = 1 м, если угол α = 30°. (1)

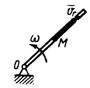
Рис. 434 Рис. 435 Рис. 436

3.4.17. Однородный стержень (рис. 436) длиной l = 1 м и массой т = 6 кг вращается с угловой ско­ростью ω = 10 рад/с. Определить кинетический момент стержня относительно центра О. (20)

3.4.18. Тонкостенная труба (рис. 437) массой т = 10 кг ка­тится по горизонтальной плоскости с угловой скоростью ω = 10 рад/с. Определить кинети­ческий момент цилиндра относительно мгно­венной оси вращения, если радиус r = 10 см. (2)

 

 

Рис. 437 Рис. 438 Рис. 439

3.4.19. Кривошип ОА (рис. 438) вращается с постоян-ной угловой скоростью ω = 6 рад/с. Колесо 2 ка­тится по неподвижному колесу 1. Определить кинетический момент колеса 2 относительно его мгновенного центра скоростей К, если радиус r = 0,15 м. Колесо 2 считать однород­ным диском массой т = 3 кг. (1,22)

3.4.20. Конус катится по неподвижной плоскости без скольжения (рис. 439). Скорость центра основания конуса v_C = 0,9 м/с, радиус r = 30 см. Опре­делить модуль кинетического момента конуса относительно мгновенной оси вращения, если его момент инерции относительно этой оси равен 0,3 кг·м². (1,04)

Рис. 440 Рис. 441

3.4.21. В плоскости Оху (рис. 440) движутся мате-риальные точки M ₁ и M ₂, массы которых m ₁ = m ₂ = 1 кг. Определить кинетический момент дан­ной системы мате-риальных точек относительно точки О в положении, когда скорости v ₁ = 2 v ₂ = 4 м/с, расстояния ОМ ₁= 2 ОМ ₂ = = 4 м и углы a ₁= α ₂ = 30°. (6)

3.4.22. Материальные точки M ₁, М ₂, М ₃, массы которых m ₁ = m ₂ = m ₃ = 2 кг, движутся по окружности радиуса r = 0,5 м (рис. 441). Определить кинетический момент системы материальных точек относительно центра О окружности, если их скорости v ₁= 2 м/с, v ₂ = 4 м/с, v ₃ = 6 м/с. (12)

 

3.4.3. Теорема об изменении кинетического момента систе­мы

Кинетический момент механической системы относительно неподвижного центра равен геометрии-ческой сумме момента относительно этого центра количества движения системы, условно приложенного в центре масс, и кинетического момента системы относительно центра масс в ее относительном движении по отношению к центру масс.

.

Теорема об изменении кинетического момента систе­мы чаще всего применяется для исследования движения механической системы, состоящей из основного тела, несущего другие тела, при условии, что тело-носитель со­вершает вращательное движение относительно неподвиж­ной оси или неподвижной точки (в частности, относи­тельно центра масс), а движения несомых тел по отно­шению к основному заданы. При этом рекомендует-ся следующая последовательность решения задачи.

1. Изобразить материальную систему в промежуточ­ный (или заданный) момент времени.

2. Изобразить на рисунке приложенныек системе внешние силы.

3. Провести оси координат. Их начало и их направле­ния выбираются таким образом, чтобы суммы моментов внешних сил (активных и реакций) относительно наи­большего количества осей равнялись нулю. Если этого осуществить нельзя, то оси проводятся наиболее естест­венным образом, причем одна из них проводится вдоль оси вращения основного тела.

4. Записать формулы теоремы об изменении кинетиче­ского момента в проекциях на выбранные оси координат:

, , .(a)

5. Вычислить кинетические моменты системы L_x, L_y, L_z относительно осей для текущего момента времени, под­ставить их значения в уравнения теоремы и получить дифференциальные уравнения движения системы.

6. Используя дифференциальные уравнения, найти ве­личины, подлежащие определению.

7. Если одна из правых частей уравнений (a) рав­на нулю, то относительно соответствующей оси выполня­ется закон сохранения кинетического момента системы/

Например, если , то L_х = const = L_{x 0}. В этом случае решение задачи сводится к определению кинети­ческого момента системы в начальный и текущий (или заданный) моменты времени и приравниванию этих зна­чений друг другу.

Пример 1. Круглая однородная горизонтальная платфор-ма радиусом r = √ 3 м и массой m ₁= 20 кг вращается без трения вок­руг вертикальной оси с угловой скоростью ω = 2рад/с (рис. 442). В точке А на ободе платформы находится материальная точка К массой m ₂ = 10кг. В некоторый момент времени (t = 0) эта точка начинает двигаться по хорде АВ платформы с постоянной относительной скоростью v_r = 4 м/с. Определить угловую скорость плат­формы, когда точка К попадает в точку В хорды АВ.

Решение. Изобразим механическую систему, состоящуюизплатформы и точки, в положении, когда материальная точка К находится в точке В платформы. В этот момент угловая ско­рость платформы равна ω. Изобразим внешние силы: силы тяжести , и реакции подши-пников . Все они или параллельны оси вращения, или пересекают ее, следова­тельно, их моменты относительно этой оси равны нулю. Поэтому проведем ось z вдоль оси вращения платформы и составим уравнение теоремы об из­менении кинетического момента систе­мы в проекциях на эту ось:

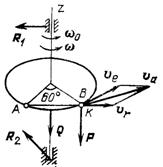
= 0,

т. е. выполняется закон сохранения кинетического момента си­стемы относительно оси z, поэтому

L_z = L_z0,

и задача сводится к подсчету кинетического момента в началь-ный момент и в момент, когда точка К достигла точки В хорды

Рис. 442 АВ.

Так как система состоит из двух тел, то ее кинетический мо­мент относительно оси z равен сумме кинетических моментов плат­формы и точки:

L_{z точ} =L_{z пл} + l_{z точ}.

При подсчете кинетические моментов следует помнить, что вих выражения входят абсолютные скорости. Относи-тельная скорость точки К нам задана: v_r = 4 м/с, а переносная — скорость точки В платформы — равна v_e = ωr. Поэтому

l_{z точ} = т ₂ v_rr cos 30˚ + m ₂ ωr ₂ ..

Для платформы кинетический момент определяется как для твер­дого тела относительно его оси вращения:

.

Тогда

.

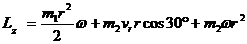В начальный момент точка К относительно платформы не двига­лась, т. е. v_r0 = 0, поэтому

.

Приравнивая значения кинетических моментов системы для двух положений точки К получаем

= ,

откуда

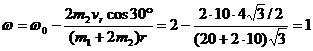рад/с.

Пример 2 Однородный блок Е массой т ₁ и радиусом r мо­жет вращаться вокруг горизонтальной оси Оz (рис 443). Через блок перекинута гибкая нерастя­жимая нить на конце А кото-рой подвешен груз М массой т ₂, а ко­нец В прикреплен к пружине BD жесткостью с. Конец D пружины закреплен неподвижно. Найти закон движения груза М, если в началь-ный момент он находился в положении статического равно­весия и имел скорость v₀ направ­ленную вертикально вниз. Тре­нием и проскаль-зыванием нити по блоку пренебречь.

Решение. Изобразим систе­му, состоящею из блока и груза, в произвольный момент времени. Изобразим на схеме действую­щие на систему внешние силы силы тяжести

Рис. 443 , ,

силу упругости пружины 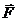и реакцию оси блока 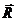, неизвест-ную ни по модулю, ни по направлению Положение блока определяется его углом поворота φ а положение груза – координатой s. Проскальзывание нити по блоку отсутствует и поэтому φr = s. Вы­берем начало отсчета φ и s в положении статического равновесия системы. В этом положении пружина уже имеет деформацию рав­ную δ_ст. Поэтому для изобра-женного на схеме положения дефор­мация пружины равна δ = δ_ст+ s,а сила упругости пружины F = cδ = c (δ_ст + s).

Для данной системы нельзя провести ось, относительно которой сумма моментов внешних сил равна нулю. Оси, расположенные в плоскости чертежа, рассматривать нельзя, так как относительно их и кинетический момент системы тождественно равен нулю. Поэтому для исключения из рассмотрения неизвестной реакции оси блока составим уравнение теоремы об изменении кинетиче­ского момента системы в проекции на эту ось.

,

(здесь мы использовали равенство F_ст = с δ_ст = Q).

Определим для рассматриваемого положения системы ее кине­тический момент

L_z = L_zM + L_zE

тело М движется поступательно, поэтому его кинетический момент относительно оси Оz равен мо­менту его количества движения относительно точки О:

L_zM = m ₂ vr,а кинетический момент блока относительно его оси вращения ра­вен произведению его момента инерции относительно этой оси на угловую скорость

L_zE = J_zω = m ₁ r ² ω /2 = m ₁ r v/ 2 (здесь мы исполь­зовали равенство ω = v / r). Итак,

.

Подставив это выражение в формулу теоремы, получим

.

Поскольку ,а 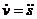то, перенеся все слагаемые в левую часть и разделив на коэффициент, стоящий перед , получим

.

Положим 2с/(2 m ₂+ m ₁) = k ², тогда уравнение, описываю-щее дви­жение тела М, примет вид дифферен­циального уравнения гармонических колебаний

,

решением которого является

s = C ₁cos kt + C ₂sin kt.

Определив предварительно , по началь­ным условиям (t = 0, s ₀ = 0, = v ₀) найдем постоянные C ₁и С ₂.

= - C ₁ k sin kt + C ₂ k cos kt, s ₀ = 0 = C ₁, = v ₀ = C ₂ k.

Тогда C ₁= 0, C ₂ = v ₀ /k, и закон движе­ния груза М принимает вид

.

Пример 3. Горизонтальная платформа A массой т ₁ = 9 кг закреплена на упругом стержне ОО ₁ (рис. 444) и может совер-шать крутильные колебания вокруг вертикальной оси ОО ₁, относительно которой радиус инерции платформы равен ρ. По платформенанеизменном расстоянии а от точки О движется материальная точ­ка К массой т ₂ = т так что

К ₀ К = s = 0,27 a sin pt.

Найти вынуж­денные колеба-ния платформы, если жесткость стержня ОО ₁ при кручении равна

с = amg, ρ = а, р = .

Решение. Если мы повернем платформу на угол φ вокруг оси ОО ₁, то на нее со стороны упру-гого стержня будет действовать пара сил с моментом М = сφ, стремящимся вернуть платформу в

Рис. 444 исходное положение, при котором стержень ОО ₁ не деформирован, т. е. не закручен. Таким обра-зом, внешними силами, действующи­ми на рассматриваемую систему, состоящую из платформы А и точки К, являются силы тяжести Р = 9 тg, Q = тg и реакция упругого стержня (произвольно направленные силы и момент). Так как основное тело — платформа — совершает вращательное движение вокруг оси ОО ₁,

для решения задачи применим теорему об изменении кинетического момента системы относительно этой оси, кото-рую обозначим Oz. Тогда в правую часть уравнения вой­дет только составляющая М реактивного момента, направленная противоположно углу поворота платформы: таким образом,

.

Определим кинетический момент системы для ее текущего поло­жения:

L_z = L_zА + L_zK = J_zω + M_z (m ₂ ),

где — абсолютная скорость точки К,

v_e — пере­носная скорость точки К,

v_r = s = 0,27 ap cos pt — относительная скорость точки К. Из чертежа видно, что v_е и v_r направлены вдоль одной прямой в одну и ту же сторону, поэтому

v_а = v_e + v_r == ωа + 0,27 ар cos pt.

Следовательно,

M_z (m ₂ ) = m ₂ v_aa = m₂ (ω + 0,27 р cos pt) a ²,

L_z = m ₁ ρ ² ω + m ₂(ω + 0,27 p cos pt) a ².

Подставив последнее выражение в формулу теоремы, получим

,

или

.

Введем обозначения:

,

.

Тогда уравнение движения платформы имеет вид

.

Это дифференциальное уравнение вынужденных колебаний; его частное решение, определяющее вынужденные колебания при отсутствии резонанса (k ≠ p) запишется так:

.

В этой задаче мы опять встретились со случаем кинематического возбуждения колебаний.

Задачи

3.4.23. Материальная точка массой0,5кг движется в плоскости согласно уравнениям х = 2 t, y = 4 t. Опреде-лить момент равнодействующей всех приложенных к этой точке сил относительно начала координат в момент времени t = 1 с. (8)

3.4.24. Материальная точка массой 0,5 кг движется по закону . Определить момент равнодей-ствующей всех приложенных к этой точке сил относи-тельно начала координат. (8)

3.4.25. Материальная точка массой 1 кг движется по закону . Определить момент равно-действующей вех приложенных к этой сил относительно оси Ох в момент времени t = 1 c. (6)

3.4.26. Спортсмен, прыгая с трамплина в воду, делает в воздухе сальто. В момент отрыва от трамплина он сообщает себе угловую скорость ω ₀ = 1, 5 рад/с вокруг горизонтальной оси, проходящей через его центр масс. При этом момент инерции спортсмена относительно оси вращения J ₀ = 13,5 кг·м². Определить угловую скорость спортсмена, когда он во время полета, поджимая руки и ноги, уменьшил момент инерции до J = 5,4 кг·м². (3,75)

3.4.27. Внутренними силами системы (рис. 445) маховик 2 массой 20 кг, центральный момент инерции которого J_z1 = 1 кг·м², раскручивается до относительной угловой скорости ω_r = 40 рад/с. Определить угловую скорость ω держателя 1, если его момент инерции J_z = 4 кг·м², размер l = 1 м. (1,6)

3.4.28. Тело вращается вокруг вертикальной оси Оz (рис. 446) под действием пары сил с моментом М = 16 t. Определить момент инерции тела относительно оси Oz, если известно, что в момент времени t = 3 с угловая скорость ω = 2 рад/с. При t = 0 тело находилось в покое. (36)

 

Рис. 445 Рис. 446 Рис. 447

3.4.29. Однородный стержень (рис. 447) массой m = 3 кг и длиной l = 1 м вращается вокруг вертикаль­ной оси Oz с угловой скоростью ω ₀ = 24рад/с. К валу ОА прикладывается постоянный мо­мент сил торможения. Определить модуль этого момента, если стержень останавливается через 4 с после начала торможения. (6)

3.4.30. Тело вращается вокруг вертикальной оси Oz под действием двух пар сил с моментами и . Момент инерции тела относительно оси Oz равен 3 кг·м². Определить угло­вую скорость тела в момент времени t = 2 с, если в начальный мо­мент тело не вращалось. (6)

3.4.31. Однородный диск радиуса r = 0,1 м и массой 5 кг (рис. 448) соединен с четырьмя стержнями длиной l = 0,5 м и массой 1 кг каждый. Сис­тема тел начинает вращаться под действием внешних сил с угловой скоростью ω = 3 t. Оп­ределить момент внешних сил относительно оси Oz. (1,79)

Рис. 448 Рис. 449 Рис. 450

3.4.32*. Круглая однородная горизонтальная плат-форма радиусом 1 м, массой 200 кг (рис. 449) вращается без трения вокруг верти­кальной оси Oz с угловой скоро-стью ω = 2 рад/с. В точке А платформы находится тело D массой 50 кг, которое можно при­нять за материальную точку. В некоторый момент времени (t = 0) тело D начи-нает двигаться по платформе по диаметру AВС с посто-янной относительной скоростью v_r = 2 м/с. Найти угло-вую скорость платформы в тот момент, когда тело находится в точке В платформы.

Ответ: ω ₁ = 2,9 рад/с.

3.4.33*. Однородный стержень массой m ₁ (рис. 450) вращается во­круг оси АВ с угловой скоростью ω ₀. По прямой ОМ движется ма­териальная точка массой т ₂, с постоянной относительной скоростью . Пренебрегая трением в подшипниках, найти угловую скорость ω стержня по истечении времени t после выхода точки из центра О.

Ответ: .

3.4.34*. Однородная круглая горизонтальная пласти-на массой 4 т (рис. 451) вращается вокруг вертикальной оси АВ, проходящей через центр О. По пластине на неиз­менном расстоянии r от оси враще­ния движется мате-риальная точка М массой т; закон относительного движе­ния точки s = r sin (πt/ 2). Трением в подшипниках можно пренебречь, R = 2 r. Найти угловую скорость и угло­вое ускорение пластины, если в началь­ный момент она была неподвижной.

Ответ:

Рис. 451 Рис. 452

3.4.37*. Однородный диск массой m ₁ закреплен на упругом стержне OO₁ (рис. 452) и мо­жет совершать крутильные колебания вокруг вертикальной оси. По ободу диска дви­жется точка М массой т ₂ по закону

М₀М = s = a sin ωt. Найти вынужденные колеба­ния диска, если стержень закручивается на один радиан при статическом действии при­ложенной к концу О пары сил с моментом с; m ₁ = 1 кг, m ₂ = 0,4 кг, а = 1 см, r = 20 см, ω =14 рад/с, с = 80 Н·см/рад.

Ответ: φ = - 0,023 sin 14 t.

3.4.35*. Груз А массой 10 кг прикреплен к тросу, намотанному на цилинд­рический барабан В радиусом 20 см. Груз падает из состояния покоя в течение двух секунд, после чего к барабану прикла­дывается постоян-ный тормозящий момент М. Считая бара­бан однородным сплошным цилиндром, найти момент, обес­печивающий остановку груза в течение последующих четырех секунд.

Ответ: М = 29,4 Н·м.

3.4. 36*. Вал В радиусом r приводитсяво вращениевокру