ДИНАМИКА
ДИНАМИКА ТОЧКИ. ДВЕ ЗАДАЧИ ДИНАМИКИ
Первая основная задача динамики материальной точки
Первая основная задача динамики точки заключается в том, что задан закон (уравнения) движения точки и ее масса, а требуется определить силу, действующую на точку.
Дано: т, x = f 1(t); y = f 2(t); z = f 3(t).
Определить 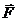 .
.
Эта задача решается дифференцированием заданных уравнений движения и подстановкой результатов дифференцирования в уравнения:
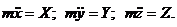 (75)
(75)
Величина и направление силы действующей на точку находится по следующим формулам:
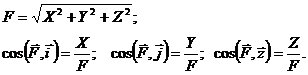 (76)
(76)
При решении первой задачи динамики нужно придер-живаться следующей последовательности действий:
1) изобразить точку в текущий момент времени;
2) изобразить активные силы, действующие на точку;
3) освободить точку от связей, заменить действие связей реакциями;
4) выбирать систему координат;
5) составить дифференциальные уравнения движения точки по формулам (75).
В тех задачах, в которых траекторией точки является окружность, дифференциальные уравнения движения выгодно брать в естественной форме:
 ; (77)
; (77)
6) найти по заданному закону движения токи проекции ускорения на оси координат по формулам:
 ; (78)
; (78)
7) подставитьнайденные величины в уравнения (75), найтипроекции силы, а по найденным проекциям силы определить величину и направление силы по формулам (76).
В частном случае прямолинейного движения точки, для упрощения решения задачи, при составлении дифференциальных уравнений движения (75) рекомендуется одну из осей координат направлять по траектории точки в сторону движения. В случае плоского движения точки систему координат хОу нужно брать в плоскости движения, причем так, чтобы координаты текущего положения точки были положительными. При составлении дифференциальных уравнений (75) касательную к траектории точки следует направлять в сторону положительного направления отсчета дуг, а главную нормаль—в сторону вогнутости траектории
Задачи
Задачи
 3.2.1*. Корпус кривошипно-ползунного механизма укреплен на гладком основании с помощью болтов (рис. 379). Кривошип вращается с постоянной угловой скоростью ω. Найти силу давления корпуса на основа-ние, а также горизонтальное усилие, воспринимаемое болта-ми при работе механизма, если ОА = АВ = l = 0,5м, масса кривошипа т 1 = 1 кг, масса шатуна m 2 = 1 кг, масса ползуна т 3 = 2 кг, масса корпуса m 4 = 5 кг, ω = 14 рад/с.
3.2.1*. Корпус кривошипно-ползунного механизма укреплен на гладком основании с помощью болтов (рис. 379). Кривошип вращается с постоянной угловой скоростью ω. Найти силу давления корпуса на основа-ние, а также горизонтальное усилие, воспринимаемое болта-ми при работе механизма, если ОА = АВ = l = 0,5м, масса кривошипа т 1 = 1 кг, масса шатуна m 2 = 1 кг, масса ползуна т 3 = 2 кг, масса корпуса m 4 = 5 кг, ω = 14 рад/с.
Ответ: N = 88,2 - 588 cos 14 t H,
Рис. 379 R = 98 sin 14 t H.
3.2.2. Положение центра масс С механической системы массой т = 50 кг определяется радиус-вектором  . Определить статический момент масс этой системы относительно плоскости Оху. (250)
. Определить статический момент масс этой системы относительно плоскости Оху. (250)
3.2.3. Определить координату хС центра масс кривошипно-ползунного механизма (рис. 380) при углах φ = 90° и α = 30°, если масса кривошипа 1 равна 4 кг, а масса шатуна 2 равна 8 кг. Шатун 2 длиной 0,8 м считать однородным стержнем. Массой ползуна 3 пренебречь.(0,231)
 3.2.4. Тело массой т = 2 кг движется по горизонтальным направляющим (рис. 381) согласно закону s = 2 t 2 + 1. Определить модуль главного вектора внешних сил, действующих на тело. (8)
3.2.4. Тело массой т = 2 кг движется по горизонтальным направляющим (рис. 381) согласно закону s = 2 t 2 + 1. Определить модуль главного вектора внешних сил, действующих на тело. (8)


Рис. 380 Рис. 381 Рис. 382
3.2.5. Тело 1 массой т = 50 кг поднимается по наклонной плоскости с помощью троса (рис. 382), наматываемого на барабан 2 радиуса R = 0,4 м. Определить модуль главного вектора внешних сил, действующих на тело 1, если угловое ускорение барабана ε = 5 рад/с2. (100)
3.2.6. Механическая система (рис. 383) движетсятак, что проекции ускорения ее центра масс С на оси координат равны аС х = 1 м/с2, аСу = 2 м/с2, аСz = 4 м/с2. Определить модуль главного вектора внешних сил, действующих на систему, если масса системы т = 40кг. (183)
3.2.7. Движение центра масс механической системы определяется радиус-вектором  (рис. 384). Определить проекцию на ось Оу главного вектора внешних сил в момент времени t = 0,5 с, если масса системы m = 10 кг. (-197)
(рис. 384). Определить проекцию на ось Оу главного вектора внешних сил в момент времени t = 0,5 с, если масса системы m = 10 кг. (-197)



Рис. 383 Рис. 384 Рис. 385
3.2.8. Диск массой т = 20 кг вращается равномерно вокруг неподвижной оси с угловой скоростью ω = 10 рад/с (рис. 385). Определить модуль главного вектора внешних сил, приложенных к диску, если его центр тяжести удален от оси вращения на расстояние ОС = 0,5 см. (10)
3.2.9. Центр масс колеса С (рис. 386) движется по окружности радиуса R = 1,3 м согласно закону s = 4 t. Определить модуль главного вектора внешних сил, приложенных к колесу, если его масса т = 15 кг. (185)

 3.2.10. Кривошип 1 шарнирного параллелограмма (рис. 387) вращается равномерно с угловой скоростью ω = 5 рад/с. Определить модуль главного вектора внешних сил, действующих на звено 2, если его масса т = 8кг, длина ОА = 0,4 м. (80)
3.2.10. Кривошип 1 шарнирного параллелограмма (рис. 387) вращается равномерно с угловой скоростью ω = 5 рад/с. Определить модуль главного вектора внешних сил, действующих на звено 2, если его масса т = 8кг, длина ОА = 0,4 м. (80)
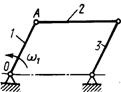
Рис. 386 Рис. 387 Рис. 388
3.2.11. Однородный равносторонний треугольник ОАВ массой т = 5 кг (рис. 388) вращается равномерно вокруг неподвижной оси. Определить его угловую скорость ω, если главный вектор внешних сил, действующих на него, равен 300 Н, а длина l =0,4м. (16,1)
3.2.12. Шкив 2 (рис. 389)радиуса R = 0,2 м, вращаясь с угловым ускорением ε2 = 10 рад/с2, поднимает однород-ный цилиндр 1, масса которого т = 50 кг. Определить модуль главного вектора внешних сил, действующих на цилиндр. (50)
3.2.13. Однородный диск радиуса (рис. 390) R = 0,5 м, масса которого т = 20 кг, вращается с постоянным угловым ускорением ε = 10 рад/с2. Определить модуль главного вектора внешних сил, действующих на диск. (0)



Рис. 389 Рис. 390 Рис. 391
3.2.14. Однородный стержень ОА (рис. 391) массой т = 10 кг вращается равномерно с угловой скоростью ω = 10 рад/с. Определить модуль главного вектора внешних сил, действующих на стержень, если его длина ОА = 1 м. (500)
3.2.15. Ползун А (рис. 392) движется под действием силы 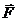 с постоянной скоростью
с постоянной скоростью 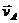 . Определить реакцию направляющей на ползун А в тот момент времени, когда ускорение ползуна В равно аB = 4 м/с2, если масса однородного стержня АВ равна 5 кг. Массой ползунов пренебречь. (10)
. Определить реакцию направляющей на ползун А в тот момент времени, когда ускорение ползуна В равно аB = 4 м/с2, если масса однородного стержня АВ равна 5 кг. Массой ползунов пренебречь. (10)
3.2.16. Кривошип 1 (рис. 393) длиной ОА = 0,25 м, вращаясь равномерно с угловой скоростью ω = 10 рад/с, приводит в движение кулису 2, масса которой т = 5 кг. Определить модуль главного вектора внешних сил, действующих на кулису в момент времени; когда угол φ = 60°. (62,5)


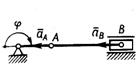
Рис. 392 Рис. 393 Рис. 394
3.2.17. Определить модуль главного вектора внешних сил, действующих на шатун АВ кривошипно-ползунного механизма (рис. 394) в момент времени, когда угол φ = 180°, а точки А и В имеют ускорения аA = 10 м/с2, aB = 14 м/с2. Шатун массой т = 5 кг считать однородным стержнем. (60)
3.2.18. Определить проекцию ускорения центра масс С механической системы (рис. 395) на ось Оу в момент времени, когда координата уC = 0,8 м, если масса системы т = 10 кг, а главный вектор приложенных внешних сил  . В начальный момент времени центр масс системы находился в точке О в покое. (1,2)
. В начальный момент времени центр масс системы находился в точке О в покое. (1,2)
3.2.19. Тело 1 массой 4кг может двигаться по горизонтальной направляющей (рис. 396). На какое расстояние переместится тело 1, когда однородный стержень 2 массой 2 кг и длиной l = 0,6 м, опускаясь под действием силы тяжести, займет вертикальное положение. В начальный момент система находилась в покое. (0,1)
3.2.20. Тело 1 массой m = 0,7 кг (рис. 397) может двигаться по горизонтальной направляющей. Определить модуль ускорения тела 1 в момент времени t = 0,25 с, если относительно него под действием внутренних сил системы движется тело 2 массой т = 0,1 кг согласно 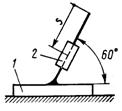

 уравнению s = sin 4 t. (0,841)
уравнению s = sin 4 t. (0,841)
Рис. 395 Рис. 396 Рис. 397
3.2.21. На тело 1 (рис. 398) действует постоянная сила F = 10 Н. Определить ускорение этого тела в момент времени t = 0,5 с, если относительно него под действием внутренних сил системы движется тело 2 согласно уравнению х = cos π t. Массы тел: m 1 = 4 кг, m 2 = 1 кг. Тела движутся поступательно. (2)


Рис. 398 Рис. 399
3.2.22. Определить ускорение тела 1 (рис. 399), скользящего по гладкой наклонной плоскости, если в горизонтальных направляющих относительно него под действием внутренних сил системы движется тело 2 согласно уравнению х = t 2. Массы тел: m 1 = m 2 = 1 кг. Тела движутся поступательно. (4,04)
3.3. ТЕОРЕМА ОБ ИЗМЕНЕНИИ
КОЛИЧЕСТВА ДВИЖЕНИЯ
Производная по времени от количества движения системы материальных точек равна главному вектору внешних сил действующих на систему
 ,
,
или в дифференциальной форме: Дифференциал количества движения системы материальных точек равен векторной сумме элементарных импульсов действующих на систему внешних сил
 .
.
Решение задач с помощью теоремы об изменении количества движения по сравнению с решением задач с использованием дифференциальных уравнений движения системы упрощается, поскольку применение теоремы исключает необходимость рассмотрения внутренних сил системы. Решение оказывается особенно простым в том случае, когда выполняется закон сохранения количества движения.
Решение задачи с помощью теоремы обизменении количества движения рекомендуется проводить в следующей последовательности.
1. Изобразить систему в положении, которое она занимает в промежуточный момент времени (t > 0).
2. Изобразить на рисунке все приложенные к системе внешние силы (как активные, так и реакции связей).
3. Провести оси координат. Если на систему действуют только параллельные силы, то одна из осей проводится перпендикулярно направлению действия сил, в противном же случае оси проводятся наиболее естественным способом, вытекающим из условия задачи. Начало координат следует совместить с положением основного тела при t = 0 или с положением его статического равновесия.
4. Составить уравнения теоремы об изменении количества движения в проекциях на выбранные, оси координат в дифференциальной форме:
dQх/dt = 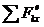 , dQy/dt=
, dQy/dt=  , dQz/dt =
, dQz/dt = 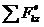 ,
,
или в интегральной форме:
 ,
,  ,
,  .
.
4. Изобразить на рисунке абсолютные и относительные скорости тел системы и подсчитать проекции количества движения системы на оси координат. Необходимо иметь в виду, что в выражения
 ,
,  ,
, 
входят абсолютные скорости. Если направление скорости какой-либо точки заранее неизвестно, то скорость направляют в сторону положительных направлений осей координат.
6. Подставив выражения проекций количества движения системы в формулы теоремы (п. 4), определить неизвестные силы пли получить дифференциальные уравнения движения интересующей нас части системы.
7. Проинтегрировать полученные дифференциальные уравнения и найти искомые неизвестные.
8. Если выполняется закон сохранения количества движения или какой-либо его проекции (т. е. если  = 0 или
= 0 или 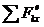 = 0 и, следовательно,
= 0 и, следовательно,  = const =
= const =  или
или
Qx= const = Qx0), то задача сводится к определению количеств движения системы (или их проекции) в начальный и заданный (или текущий) моменты времени и приравниванию их друг другу
Пример 1. На железнодорожной платформе, свободно стоящей на рельсах, установлена лебедка А с барабаном радиусом r (рис. 400). Лебедка предназначена для перемещения по платформе груза B массой т 1. Масса платформы с лебедкой m 2. При включении лебедки барабан вращается по закону, ω = f (t) рад/с. В начальный момент система неподвижна. Пренебрегая трением, найти закон изменения скорости платформы после включения лебедки.
 Решение. Чтобы исключить неизвестные силы взаимодействия между лебедкой и платформой, лебедкой и грузом, грузом и платформой, рассмотрим платформу, лебедку и груз как единую механическую систему. Тогда все внешние силы, действующие на эту систему (силы тяжести
Решение. Чтобы исключить неизвестные силы взаимодействия между лебедкой и платформой, лебедкой и грузом, грузом и платформой, рассмотрим платформу, лебедку и груз как единую механическую систему. Тогда все внешние силы, действующие на эту систему (силы тяжести  ,
,  и реакции
и реакции  ,
,  ) будут вертикальными. Проведем ось х перпендикулярно им и запишем теорему об изменении количества движения системы в проекциях на эту ось:
) будут вертикальными. Проведем ось х перпендикулярно им и запишем теорему об изменении количества движения системы в проекциях на эту ось:
 .
.
Таким образом, мы имеем
Риc. 400 случай сохранения проекции
количества движения системы: Qx= const = Qx0, поскольку в начальный момент система неподвижна, Qx0 = 0, и решение задачи сводится к тому, чтобы найти количество движении в момент времени t > 0 и приравнять полученное выражение нулю. Обозначим скорость тележки через  и направим ее в сторону положительного направления оси х. Скорость груза В относительно платформы обозначим
и направим ее в сторону положительного направления оси х. Скорость груза В относительно платформы обозначим 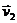 ; при этом v 2 = ωr. Абсолютная скорость груза равна vB = v 1+ v 2 = v 1 + ωr. Тогда
; при этом v 2 = ωr. Абсолютная скорость груза равна vB = v 1+ v 2 = v 1 + ωr. Тогда
Qx = m 2 v 1+ (т 1 v 1 – ωr) = 0,
откуда
 .
.
Знак минус показывает, что платформа будет перемещаться в сторону, противоположную относительному движению груза.
Пример 2. Электрический мотор массой т 1 установлен без креплений на гладком горизонтальном фундаменте (рис. 401). На валу мотора под прямым углом закреплен одним концом невесомый стержень длиной l, на другой конец стержня насажен точечный груз А массой m 2. В момент включения мотора стержень занимает вертикальное положение. После включения мотора угловая скорость его вала постоянна и равна ω. найти:
 1) горизонтальное движение мотора; 2) силу давления мотора на фундамент.
1) горизонтальное движение мотора; 2) силу давления мотора на фундамент.
Решение. Изобразим мотор в положении φ = ωt > 0. К системеприложены внешние силы: силы тяжести  ,
,  и реакция фундамента
и реакция фундамента 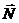 . Все они
. Все они
Рис. 401вертикальны, поэтому ось х проведем горизонтально. Начало отсчета выберем в положении, которое занимает центр мотора при φ = 0, т. е. при t = 0. Запишем теорему в проекциях на оси координат:
dQх/dt = 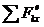 ,
,
следовательно, Qх = const = Qх0 = 0, так как до включения мотор и груз А были неподвижны; dQу/dt = =  = N- Р - Q, откуда N = g (m1+ m2)+ dQy/dt. Таким образом, задача сводится к определению проекций количества движения системы. Пусть центр мотора движется вправо со скоростью vc, тогда
= N- Р - Q, откуда N = g (m1+ m2)+ dQy/dt. Таким образом, задача сводится к определению проекций количества движения системы. Пусть центр мотора движется вправо со скоростью vc, тогда
Qx = m 1 vc + m 2 vAx, Qу = m 2 vAy,,
где 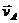 — абсолютная скорость груза А. Переносной скоростью груза является скорость мотора
— абсолютная скорость груза А. Переносной скоростью груза является скорость мотора  , относительной — скорость при вращении груза А вокруг точки С: vr = ωl. Тогда vAx = vс – ωl cos ωt, vAу =- ωl sin ωt и, следовательно,
, относительной — скорость при вращении груза А вокруг точки С: vr = ωl. Тогда vAx = vс – ωl cos ωt, vAу =- ωl sin ωt и, следовательно,
Qx = (m1 + m2) vc - m2ωl cos ωt, Qy = - m2 ωl sin ωt.
Так как Qх = 0, получаем, что
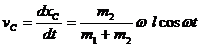
откуда  + С. Из начальных условий (t = 0, хС = 0) находим С = 0 и окончательно
+ С. Из начальных условий (t = 0, хС = 0) находим С = 0 и окончательно
 ,
,
т. е. центр мотора будет совершать горизонтальные гармонические колебания относительно своего начального положения с амплитудой m 1 l/ (m 1 + т 2). Сила давления мотора на фундамент по величине равна реакции фундамента, действующей на мотор, поэтому
N = g (т 1+ m 2) +  = g (т 1 + т 2) - m 2 ω2l cos ωt).
= g (т 1 + т 2) - m 2 ω2l cos ωt).
Минимальное значение реакции достигается при cos ωt = 1, т. е. при φ = 0, а максимальное — при φ = π:
Nmin = g (m 1 — m 2) + т 2 ω 2 l, Nmax = g (m 1+ m 2) + m 2 ω 2 l.
Если Nmin < 0, то мотор начинает подпрыгивать на фундаменте. В этом случае его угловаяскорость
 .
.
Пример 3. Призма А массой т 1 лежит на гладкой наклон-ной плоскости. По ней движется тело В массой т 2 причем это относительное движение происходит по закону s = nt 2 / 2. В начальный момент тело А находится в покое. Определить зависимость скорости тела А от времени (рис. 402).
Решение. Система состоит из двух тел: А и В. На нее действуют следующие внешние силы:  - сила тяжести тела А,
- сила тяжести тела А,  - сила тяжести тела В,
- сила тяжести тела В, 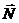 - реакция наклонной плоскости. Для решения задачи применим теорему об изменении количества движения системы в интегральной форме в проекциях на ось х:
- реакция наклонной плоскости. Для решения задачи применим теорему об изменении количества движения системы в интегральной форме в проекциях на ось х:
 ,
,
 где Q0x — проекция количества движения системы в начальный момент времени, а Qx — та же проекция в произвольный момент времени t.
где Q0x — проекция количества движения системы в начальный момент времени, а Qx — та же проекция в произвольный момент времени t.
Определим количество движения системы в момент t: 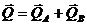 , где
, где  - количество движения тела А,
- количество движения тела А,  — количество движения тела В,
— количество движения тела В, 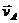 и
и  — абсолютные скорости тел А и В.
— абсолютные скорости тел А и В.
Для тела В переносной
Рис.402 скоростью является скорость тела А ( ), а относительная скорость
), а относительная скорость  nt, следовательно,
nt, следовательно,
 .
.
Проекция количества движения системы на ось х равна
Qx = (m 1+ m 2) vA + m 2 nt cos β.
По условию при t = 0, va = 0, и поэтому Qх0 = 0. Определим проекции импульсов внешних сил на ось х за время t:
 ,
,
 ,
,
 , так как Nx= 0.
, так как Nx= 0.
Подставив найденные величины в формулу теоремы, получим
(m 1 + m 2) vА + т 2 пt cos β = g (m 1+ m 2) t sin α,
или
 .
.
Таким образом, скорость призмы А пропорциональна времени, а ее направление зависит от знака выражения, стоящего в скобках. Призма будет двигаться вверх по наклонной плоскости, если g sin α – т 2 п cos β/(m 1 + m 2) < 0, т. е. если относительное ускорение аr = 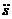 = п тела В превышает значение
= п тела В превышает значение
 .
.
Задачи
Моменты инерции
Осевые: 
Центробежные: 
Полярный  .
.
 .
.
Задачи
3.4.1. Определить момент инерции относительно плоскости Оху материальной точки массой 2 кг, если ее координаты х = 0,8 м, у = 0.6 м, z = 0,4 м. (0,32)
3.4.2. Определить момент инерции относительно плоскости Оху механической системы (рис. 425), состоящей из четырех одинаковых материальных точек, если масса каждой точки т = 1,5 кг, а радиус r = 0,4 м. (0,48)

 3.4.3. Определить момент инерции относительно оси Оу механической системы (рис. 426), состоящей из трех одинаковых материальных точек, если радиус r = 0,6 м, а масса каждой точки т = 3кг. (1,62)
3.4.3. Определить момент инерции относительно оси Оу механической системы (рис. 426), состоящей из трех одинаковых материальных точек, если радиус r = 0,6 м, а масса каждой точки т = 3кг. (1,62)

Рис. 425 Рис. 426 Рис. 427
3.4.4. Определить момент инерции относительно центральной оси Оу однородной тонкой квадратной пластины (рис. 427) массой т = 0,3 кг, имеющей отверстие радиуса r = 0,04 м. (4,89 ·10-4)
3.4.5. Определить полярный момент инерции механической системы (рис. 428), состоящей из трех одинаковых материальных точек, относительно начала координат О, если расстояние l = 0,3 м, а масса каждой точки т = 0,5 кг. (0,27)
3.4.6. Определить момент инерции однородного диска (рис. 429) относительно центра О, если его момент инерции относительно оси Ох равен 3 кг·м2. (6)
3.4.7. Определить центробежный момент инерции Jxy материальной точки массой 0,5 кг относительно осей Ох, Оу, если координаты точки х = 0,4 м, у = -0,5 м, z = 0,4 м. (-0,1)



Рис. 428 Рис. 429 Рис. 430
3.4.8. Определить центробежный момент инерции механической системы (рис. 430), состоящей из четырех
одинаковых материальных точек, относительно осей Ох, Оу, если расстояния l 1 = 0,4 м, l 2 = 0,8 м, а масса каждой точки т = 2 кг. (0,64)
3.4.9. Определить центробежный момент инерции механической системы (рис. 431), состоящей из двух материальных точек, относительно осей Ох, Оу. Массы точек т 1 = 1 кг, т 2 = 2 кг, расстояние l = 0,5 м. (-0,325)


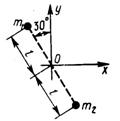
Рис. 431 Рис. 432 Рис. 433
3.4.10. Определить центробежный момент инерции Jxy однородного конуса (рис. 432) относительно осей Оу, Oz. (0)
3.4.11. Определить радиус инерции тела (рис. 433) массой т = 150 кг относительно оси Oz, если его момент инерции относительно этой оси равен 1,5 кг·м2. (0,1)
Кинетический момент системы
Кинетическим моментом системы называют главный момент количества движения всех точек системы:
 .
.
Кинетический момент твердого тела относительно неподвижной оси его вращения определяют формулой 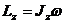
Задачи
3.4.12. Материальная точка массой т = 0,5 кг движется по оси Оу согласно уравнению у = 5 t 2. Определить момент количества движения этой точки относительно центра О в момент времени t = 2 c. (0)
3.4.13. Материальная точка массой т = 1 кг движется по закону: х = 2 t, у = t 3, z = t 4. Определить момент количества движения этой точки относительно оси Оу в момент времени t = 2 с. (-96)
3.4.14. Скорость материальной точки массой т = 1кг определяется выражением  . Определить модуль момента количества движения точки относитель-но начала координат в момент времени t = 2 с, когда ее координаты х = 2м, у = 3 м, z = 3 м. (10,0)
. Определить модуль момента количества движения точки относитель-но начала координат в момент времени t = 2 с, когда ее координаты х = 2м, у = 3 м, z = 3 м. (10,0)
3.4.15. Трубка (рис. 434) равномерно вращается с угловой скоростью ω = 10 рад/с. По трубке движется шарик массой m = 1 кг. Определить момент количества движения шарика относительно оси вращения трубки, когда расстояние ОМ = 0,5 м и скорость шарика относительно трубки vr = 2 м/с. (2,5)
3.4.16. Конус (рис. 435) вращается равномерно вокруг оси Az с угловой скоростью ω = 4 рад/с. По образующей конуса движется материальная точка М массой
1 кг. Определить момент количества движения материальной точки относительно оси Oz в положении, когда расстояние ОМ = 1 м, если угол α = 30°. (1)

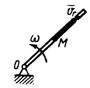

Рис. 434 Рис. 435 Рис. 436
3.4.17. Однородный стержень (рис. 436) длиной l = 1 м и массой т = 6 кг вращается с угловой скоростью ω = 10 рад/с. Определить кинетический момент стержня относительно центра О. (20)
3.4.18. Тонкостенная труба (рис. 437) массой т = 10 кг катится по горизонтальной плоскости с угловой скоростью ω = 10 рад/с. Определить кинетический момент цилиндра относительно мгновенной оси вращения, если радиус r = 10 см. (2)



Рис. 437 Рис. 438 Рис. 439
3.4.19. Кривошип ОА (рис. 438) вращается с постоян-ной угловой скоростью ω = 6 рад/с. Колесо 2 катится по неподвижному колесу 1. Определить кинетический момент колеса 2 относительно его мгновенного центра скоростей К, если радиус r = 0,15 м. Колесо 2 считать однородным диском массой т = 3 кг. (1,22)
 3.4.20. Конус катится по неподвижной плоскости без скольжения (рис. 439). Скорость центра основания конуса vC = 0,9 м/с, радиус r = 30 см. Определить модуль кинетического момента конуса относительно мгновенной оси вращения, если его момент инерции относительно этой оси равен 0,3 кг·м2. (1,04)
3.4.20. Конус катится по неподвижной плоскости без скольжения (рис. 439). Скорость центра основания конуса vC = 0,9 м/с, радиус r = 30 см. Определить модуль кинетического момента конуса относительно мгновенной оси вращения, если его момент инерции относительно этой оси равен 0,3 кг·м2. (1,04)

Рис. 440 Рис. 441
3.4.21. В плоскости Оху (рис. 440) движутся мате-риальные точки M 1 и M 2, массы которых m 1 = m 2 = 1 кг. Определить кинетический момент данной системы мате-риальных точек относительно точки О в положении, когда скорости v 1 = 2 v 2 = 4 м/с, расстояния ОМ 1= 2 ОМ 2 = = 4 м и углы a 1= α 2 = 30°. (6)
3.4.22. Материальные точки M 1, М 2, М 3, массы которых m 1 = m 2 = m 3 = 2 кг, движутся по окружности радиуса r = 0,5 м (рис. 441). Определить кинетический момент системы материальных точек относительно центра О окружности, если их скорости v 1= 2 м/с, v 2 = 4 м/с, v 3 = 6 м/с. (12)
3.4.3. Теорема об изменении кинетического момента системы
Кинетический момент механической системы относительно неподвижного центра равен геометрии-ческой сумме момента относительно этого центра количества движения системы, условно приложенного в центре масс, и кинетического момента системы относительно центра масс в ее относительном движении по отношению к центру масс.
 .
.
Теорема об изменении кинетического момента системы чаще всего применяется для исследования движения механической системы, состоящей из основного тела, несущего другие тела, при условии, что тело-носитель совершает вращательное движение относительно неподвижной оси или неподвижной точки (в частности, относительно центра масс), а движения несомых тел по отношению к основному заданы. При этом рекомендует-ся следующая последовательность решения задачи.
1. Изобразить материальную систему в промежуточный (или заданный) момент времени.
2. Изобразить на рисунке приложенныек системе внешние силы.
3. Провести оси координат. Их начало и их направления выбираются таким образом, чтобы суммы моментов внешних сил (активных и реакций) относительно наибольшего количества осей равнялись нулю. Если этого осуществить нельзя, то оси проводятся наиболее естественным образом, причем одна из них проводится вдоль оси вращения основного тела.
4. Записать формулы теоремы об изменении кинетического момента в проекциях на выбранные оси координат:
 ,
,  ,
,  .(a)
.(a)
5. Вычислить кинетические моменты системы Lx, Ly, Lz относительно осей для текущего момента времени, подставить их значения в уравнения теоремы и получить дифференциальные уравнения движения системы.
6. Используя дифференциальные уравнения, найти величины, подлежащие определению.
7. Если одна из правых частей уравнений (a) равна нулю, то относительно соответствующей оси выполняется закон сохранения кинетического момента системы/
Например, если  , то Lх = const = Lx 0. В этом случае решение задачи сводится к определению кинетического момента системы в начальный и текущий (или заданный) моменты времени и приравниванию этих значений друг другу.
, то Lх = const = Lx 0. В этом случае решение задачи сводится к определению кинетического момента системы в начальный и текущий (или заданный) моменты времени и приравниванию этих значений друг другу.
Пример 1. Круглая однородная горизонтальная платфор-ма радиусом r = √ 3 м и массой m 1= 20 кг вращается без трения вокруг вертикальной оси с угловой скоростью ω = 2рад/с (рис. 442). В точке А на ободе платформы находится материальная точка К массой m 2 = 10кг. В некоторый момент времени (t = 0) эта точка начинает двигаться по хорде АВ платформы с постоянной относительной скоростью vr = 4 м/с. Определить угловую скорость платформы, когда точка К попадает в точку В хорды АВ.
Решение. Изобразим механическую систему, состоящуюизплатформы и точки, в положении, когда материальная точка К находится в точке В платформы. В этот момент угловая скорость платформы равна ω. Изобразим внешние силы: силы тяжести 
 , и реакции подши-пников
, и реакции подши-пников  . Все они или параллельны оси вращения, или пересекают ее, следовательно, их моменты относительно этой оси равны нулю. Поэтому проведем ось z вдоль оси вращения платформы и составим уравнение теоремы об изменении кинетического момента системы в проекциях на эту ось:
. Все они или параллельны оси вращения, или пересекают ее, следовательно, их моменты относительно этой оси равны нулю. Поэтому проведем ось z вдоль оси вращения платформы и составим уравнение теоремы об изменении кинетического момента системы в проекциях на эту ось:
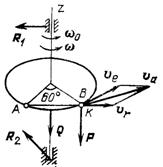
 = 0,
= 0,
т. е. выполняется закон сохранения кинетического момента системы относительно оси z, поэтому
Lz = Lz0,
и задача сводится к подсчету кинетического момента в началь-ный момент и в момент, когда точка К достигла точки В хорды
Рис. 442 АВ.
Так как система состоит из двух тел, то ее кинетический момент относительно оси z равен сумме кинетических моментов платформы и точки:
Lz точ =Lz пл + lz точ.
При подсчете кинетические моментов следует помнить, что вих выражения входят абсолютные скорости. Относи-тельная скорость точки К нам задана: vr = 4 м/с, а переносная — скорость точки В платформы — равна ve = ωr. Поэтому
lz точ = т 2 vrr cos 30˚ + m 2 ωr 2 ..
Для платформы кинетический момент определяется как для твердого тела относительно его оси вращения:
 .
.
Тогда
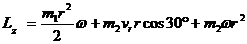 .
.
В начальный момент точка К относительно платформы не двигалась, т. е. vr0 = 0, поэтому
 .
.
Приравнивая значения кинетических моментов системы для двух положений точки К получаем
 =
=  ,
,
откуда
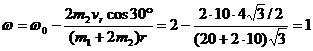 рад/с.
рад/с.
 Пример 2 Однородный блок Е массой т 1 и радиусом r может вращаться вокруг горизонтальной оси Оz (рис 443). Через блок перекинута гибкая нерастяжимая нить на конце А кото-рой подвешен груз М массой т 2, а конец В прикреплен к пружине BD жесткостью с. Конец D пружины закреплен неподвижно. Найти закон движения груза М, если в началь-ный момент он находился в положении статического равновесия и имел скорость v0 направленную вертикально вниз. Трением и проскаль-зыванием нити по блоку пренебречь.
Пример 2 Однородный блок Е массой т 1 и радиусом r может вращаться вокруг горизонтальной оси Оz (рис 443). Через блок перекинута гибкая нерастяжимая нить на конце А кото-рой подвешен груз М массой т 2, а конец В прикреплен к пружине BD жесткостью с. Конец D пружины закреплен неподвижно. Найти закон движения груза М, если в началь-ный момент он находился в положении статического равновесия и имел скорость v0 направленную вертикально вниз. Трением и проскаль-зыванием нити по блоку пренебречь.
Решение. Изобразим систему, состоящею из блока и груза, в произвольный момент времени. Изобразим на схеме действующие на систему внешние силы силы тяжести
Рис. 443  ,
,  ,
,
силу упругости пружины 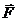 и реакцию оси блока
и реакцию оси блока 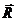 , неизвест-ную ни по модулю, ни по направлению Положение блока определяется его углом поворота φ а положение груза – координатой s. Проскальзывание нити по блоку отсутствует и поэтому φr = s. Выберем начало отсчета φ и s в положении статического равновесия систе
, неизвест-ную ни по модулю, ни по направлению Положение блока определяется его углом поворота φ а положение груза – координатой s. Проскальзывание нити по блоку отсутствует и поэтому φr = s. Выберем начало отсчета φ и s в положении статического равновесия систе



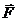 .
.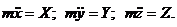 (75)
(75)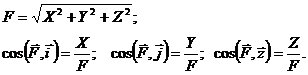 (76)
(76) ; (77)
; (77) ; (78)
; (78) 3.2.1*. Корпус кривошипно-ползунного механизма укреплен на гладком основании с помощью болтов (рис. 379). Кривошип вращается с постоянной угловой скоростью ω. Найти силу давления корпуса на основа-ние, а также горизонтальное усилие, воспринимаемое болта-ми при работе механизма, если ОА = АВ = l = 0,5м, масса кривошипа т 1 = 1 кг, масса шатуна m 2 = 1 кг, масса ползуна т 3 = 2 кг, масса корпуса m 4 = 5 кг, ω = 14 рад/с.
3.2.1*. Корпус кривошипно-ползунного механизма укреплен на гладком основании с помощью болтов (рис. 379). Кривошип вращается с постоянной угловой скоростью ω. Найти силу давления корпуса на основа-ние, а также горизонтальное усилие, воспринимаемое болта-ми при работе механизма, если ОА = АВ = l = 0,5м, масса кривошипа т 1 = 1 кг, масса шатуна m 2 = 1 кг, масса ползуна т 3 = 2 кг, масса корпуса m 4 = 5 кг, ω = 14 рад/с. . Определить статический момент масс этой системы относительно плоскости Оху. (250)
. Определить статический момент масс этой системы относительно плоскости Оху. (250) 3.2.4. Тело массой т = 2 кг движется по горизонтальным направляющим (рис. 381) согласно закону s = 2 t 2 + 1. Определить модуль главного вектора внешних сил, действующих на тело. (8)
3.2.4. Тело массой т = 2 кг движется по горизонтальным направляющим (рис. 381) согласно закону s = 2 t 2 + 1. Определить модуль главного вектора внешних сил, действующих на тело. (8)

 (рис. 384). Определить проекцию на ось Оу главного вектора внешних сил в момент времени t = 0,5 с, если масса системы m = 10 кг. (-197)
(рис. 384). Определить проекцию на ось Оу главного вектора внешних сил в момент времени t = 0,5 с, если масса системы m = 10 кг. (-197)



 3.2.10. Кривошип 1 шарнирного параллелограмма (рис. 387) вращается равномерно с угловой скоростью ω = 5 рад/с. Определить модуль главного вектора внешних сил, действующих на звено 2, если его масса т = 8кг, длина ОА = 0,4 м. (80)
3.2.10. Кривошип 1 шарнирного параллелограмма (рис. 387) вращается равномерно с угловой скоростью ω = 5 рад/с. Определить модуль главного вектора внешних сил, действующих на звено 2, если его масса т = 8кг, длина ОА = 0,4 м. (80)



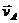 . Определить реакцию направляющей на ползун А в тот момент времени, когда ускорение ползуна В равно аB = 4 м/с2, если масса однородного стержня АВ равна 5 кг. Массой ползунов пренебречь. (10)
. Определить реакцию направляющей на ползун А в тот момент времени, когда ускорение ползуна В равно аB = 4 м/с2, если масса однородного стержня АВ равна 5 кг. Массой ползунов пренебречь. (10)


 . В начальный момент времени центр масс системы находился в точке О в покое. (1,2)
. В начальный момент времени центр масс системы находился в точке О в покое. (1,2)

 уравнению s = sin 4 t. (0,841)
уравнению s = sin 4 t. (0,841)

 ,
, .
.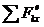 , dQy/dt=
, dQy/dt=  , dQz/dt =
, dQz/dt = 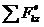 ,
, ,
,  ,
,  .
. ,
,  ,
, 
 = 0 или
= 0 или  = const =
= const =  или
или Решение. Чтобы исключить неизвестные силы взаимодействия между лебедкой и платформой, лебедкой и грузом, грузом и платформой, рассмотрим платформу, лебедку и груз как единую механическую систему. Тогда все внешние силы, действующие на эту систему (силы тяжести
Решение. Чтобы исключить неизвестные силы взаимодействия между лебедкой и платформой, лебедкой и грузом, грузом и платформой, рассмотрим платформу, лебедку и груз как единую механическую систему. Тогда все внешние силы, действующие на эту систему (силы тяжести  ,
,  и реакции
и реакции  ,
,  ) будут вертикальными. Проведем ось х перпендикулярно им и запишем теорему об изменении количества движения системы в проекциях на эту ось:
) будут вертикальными. Проведем ось х перпендикулярно им и запишем теорему об изменении количества движения системы в проекциях на эту ось: .
. и направим ее в сторону положительного направления оси х. Скорость груза В относительно платформы обозначим
и направим ее в сторону положительного направления оси х. Скорость груза В относительно платформы обозначим 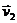 ; при этом v 2 = ωr. Абсолютная скорость груза равна vB = v 1+ v 2 = v 1 + ωr. Тогда
; при этом v 2 = ωr. Абсолютная скорость груза равна vB = v 1+ v 2 = v 1 + ωr. Тогда .
. 1) горизонтальное движение мотора; 2) силу давления мотора на фундамент.
1) горизонтальное движение мотора; 2) силу давления мотора на фундамент.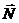 . Все они
. Все они , относительной — скорость при вращении груза А вокруг точки С: vr = ωl. Тогда vAx = vс – ωl cos ωt, vAу =- ωl sin ωt и, следовательно,
, относительной — скорость при вращении груза А вокруг точки С: vr = ωl. Тогда vAx = vс – ωl cos ωt, vAу =- ωl sin ωt и, следовательно,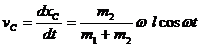
 + С. Из начальных условий (t = 0, хС = 0) находим С = 0 и окончательно
+ С. Из начальных условий (t = 0, хС = 0) находим С = 0 и окончательно = g (т 1 + т 2) - m 2 ω2l cos ωt).
= g (т 1 + т 2) - m 2 ω2l cos ωt). .
. ,
, где Q0x — проекция количества движения системы в начальный момент времени, а Qx — та же проекция в произвольный момент времени t.
где Q0x — проекция количества движения системы в начальный момент времени, а Qx — та же проекция в произвольный момент времени t.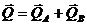 , где
, где  - количество движения тела А,
- количество движения тела А,  — количество движения тела В,
— количество движения тела В,  — абсолютные скорости тел А и В.
— абсолютные скорости тел А и В. ), а относительная скорость
), а относительная скорость  nt, следовательно,
nt, следовательно, .
. ,
, ,
, , так как Nx= 0.
, так как Nx= 0. .
.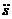 = п тела В превышает значение
= п тела В превышает значение .
.

 .
. .
.
 3.4.3. Определить момент инерции относительно оси Оу механической системы (рис. 426), состоящей из трех одинаковых материальных точек, если радиус r = 0,6 м, а масса каждой точки т = 3кг. (1,62)
3.4.3. Определить момент инерции относительно оси Оу механической системы (рис. 426), состоящей из трех одинаковых материальных точек, если радиус r = 0,6 м, а масса каждой точки т = 3кг. (1,62)






 .
.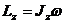
 . Определить модуль момента количества движения точки относитель-но начала координат в момент времени t = 2 с, когда ее координаты х = 2м, у = 3 м, z = 3 м. (10,0)
. Определить модуль момента количества движения точки относитель-но начала координат в момент времени t = 2 с, когда ее координаты х = 2м, у = 3 м, z = 3 м. (10,0)





 3.4.20. Конус катится по неподвижной плоскости без скольжения (рис. 439). Скорость центра основания конуса vC = 0,9 м/с, радиус r = 30 см. Определить модуль кинетического момента конуса относительно мгновенной оси вращения, если его момент инерции относительно этой оси равен 0,3 кг·м2. (1,04)
3.4.20. Конус катится по неподвижной плоскости без скольжения (рис. 439). Скорость центра основания конуса vC = 0,9 м/с, радиус r = 30 см. Определить модуль кинетического момента конуса относительно мгновенной оси вращения, если его момент инерции относительно этой оси равен 0,3 кг·м2. (1,04)
 .
. ,
,  ,
,  .(a)
.(a) , то Lх = const = Lx 0. В этом случае решение задачи сводится к определению кинетического момента системы в начальный и текущий (или заданный) моменты времени и приравниванию этих значений друг другу.
, то Lх = const = Lx 0. В этом случае решение задачи сводится к определению кинетического момента системы в начальный и текущий (или заданный) моменты времени и приравниванию этих значений друг другу.
 , и реакции подши-пников
, и реакции подши-пников  . Все они или параллельны оси вращения, или пересекают ее, следовательно, их моменты относительно этой оси равны нулю. Поэтому проведем ось z вдоль оси вращения платформы и составим уравнение теоремы об изменении кинетического момента системы в проекциях на эту ось:
. Все они или параллельны оси вращения, или пересекают ее, следовательно, их моменты относительно этой оси равны нулю. Поэтому проведем ось z вдоль оси вращения платформы и составим уравнение теоремы об изменении кинетического момента системы в проекциях на эту ось:
 = 0,
= 0, .
.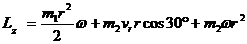 .
. .
. =
=  ,
,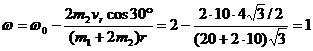 рад/с.
рад/с. Пример 2 Однородный блок Е массой т 1 и радиусом r может вращаться вокруг горизонтальной оси Оz (рис 443). Через блок перекинута гибкая нерастяжимая нить на конце А кото-рой подвешен груз М массой т 2, а конец В прикреплен к пружине BD жесткостью с. Конец D пружины закреплен неподвижно. Найти закон движения груза М, если в началь-ный момент он находился в положении статического равновесия и имел скорость v0 направленную вертикально вниз. Трением и проскаль-зыванием нити по блоку пренебречь.
Пример 2 Однородный блок Е массой т 1 и радиусом r может вращаться вокруг горизонтальной оси Оz (рис 443). Через блок перекинута гибкая нерастяжимая нить на конце А кото-рой подвешен груз М массой т 2, а конец В прикреплен к пружине BD жесткостью с. Конец D пружины закреплен неподвижно. Найти закон движения груза М, если в началь-ный момент он находился в положении статического равновесия и имел скорость v0 направленную вертикально вниз. Трением и проскаль-зыванием нити по блоку пренебречь. , неизвест-ную ни по модулю, ни по направлению Положение блока определяется его углом поворота φ а положение груза – координатой s. Проскальзывание нити по блоку отсутствует и поэтому φr = s. Выберем начало отсчета φ и s в положении статического равновесия систе
, неизвест-ную ни по модулю, ни по направлению Положение блока определяется его углом поворота φ а положение груза – координатой s. Проскальзывание нити по блоку отсутствует и поэтому φr = s. Выберем начало отсчета φ и s в положении статического равновесия систе


