

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...

Археология об основании Рима: Новые раскопки проясняют и такой острый дискуссионный вопрос, как дата самого возникновения Рима...

Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого...
Топ:
Особенности труда и отдыха в условиях низких температур: К работам при низких температурах на открытом воздухе и в не отапливаемых помещениях допускаются лица не моложе 18 лет, прошедшие...
Техника безопасности при работе на пароконвектомате: К обслуживанию пароконвектомата допускаются лица, прошедшие технический минимум по эксплуатации оборудования...
Методика измерений сопротивления растеканию тока анодного заземления: Анодный заземлитель (анод) – проводник, погруженный в электролитическую среду (грунт, раствор электролита) и подключенный к положительному...
Интересное:
Подходы к решению темы фильма: Существует три основных типа исторического фильма, имеющих между собой много общего...
Аура как энергетическое поле: многослойную ауру человека можно представить себе подобным...
Берегоукрепление оползневых склонов: На прибрежных склонах основной причиной развития оползневых процессов является подмыв водами рек естественных склонов...
Дисциплины:
|
из
5.00
|
Заказать работу |
|
|
|
|
Производной от функции 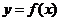 по аргументу
по аргументу 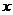 называется конечный предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:
называется конечный предел отношения приращения функции к приращению аргумента, когда последнее стремится к нулю:
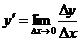 , или
, или 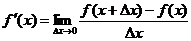
(производная обозначается также 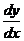 ).
).
Геометрически производная представляет собой угловой коэффициент касательной к графику функции 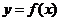 в точке
в точке 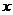 , т.е.
, т.е. 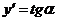 .
.
Производная есть скорость изменения функции в точке 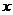 .
.
Отыскание производной называется дифференцированием функции.
Формулы дифференцирования основных функций.
| 1) | 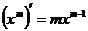
| 6) | 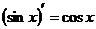
| 11) | 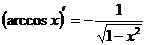
|
| 2) | 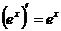
| 7) | 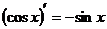
| 12) | 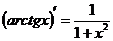
|
| 3) | 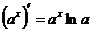
| 8) | 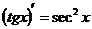
| 13) | 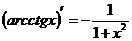
|
| 4) | 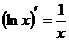
| 9) | 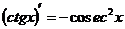
| ||
| 5) | 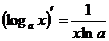
| 10) | 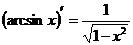
|
Основные правила дифференцирования
Пусть С – постоянная, 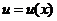 ,
, 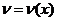 , имеющие производные. Тогда:
, имеющие производные. Тогда:
1) 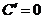
2) 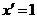
3) 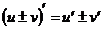
4) 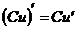
5) 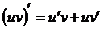
6) 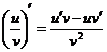
Дифференцирование сложной функции.
Если 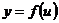 ,
, 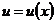 , т.е.
, т.е. 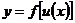 , где функции
, где функции 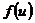 и
и 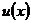 имеют производные, то
имеют производные, то
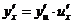
(правило дифференцирования сложной функции)
Дифференцирование неявных функций.
Пусть уравнение 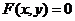 определяет
определяет 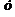 как неявную функцию от
как неявную функцию от 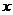 . В дальнейшем будем считать эту функцию дифференцируемой.
. В дальнейшем будем считать эту функцию дифференцируемой.
Продифференцировав по  обе части уравнения
обе части уравнения 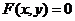 , получим уравнение первой степени относительно
, получим уравнение первой степени относительно 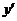 . Из этого уравнения легко находится
. Из этого уравнения легко находится 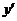 , т.е. производная неявной функции для всех значений
, т.е. производная неявной функции для всех значений 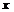 и
и 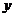 , при которых множитель при
, при которых множитель при 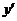 в уравнении не обращается в нуль.
в уравнении не обращается в нуль.
Примеры выполнения заданий.
Дифференцирование явных функций.
Пример 1. 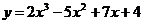 .
.
Решение:
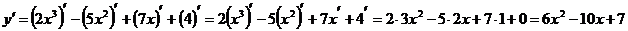 .
.
Ответ: 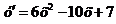
Пример 2. 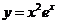 .
.
Решение:
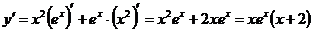 .
.
Ответ: 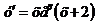 .
.
Пример 3. 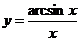 .
.
Решение:
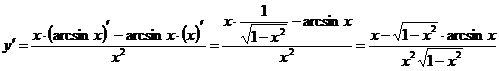 .
.
Ответ: 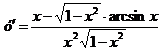 .
.
Дифференцирование сложной функции.
Пример 4. 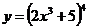 .
.
Решение:
Обозначим 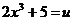 , тогда
, тогда 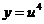 . По правилу дифференцирования сложной функции имеем
. По правилу дифференцирования сложной функции имеем
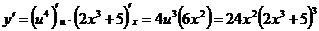 .
.
Ответ: 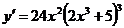 .
.
Пример 5. 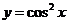 .
.
Решение:
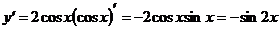
Ответ: 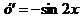 .
.
Пример 6. 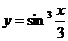 .
.
Решение:
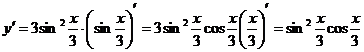
Ответ: 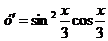 .
.
Пример 7. 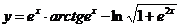 .
.
Решение:
Перепишем функцию 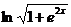 в другой вид
в другой вид 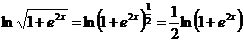 .
.
|
|
Тогда 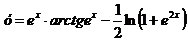 ,
,
получим
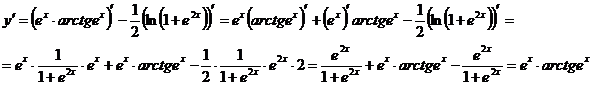 .
.
Ответ: 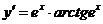 .
.
Пример 8. 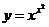 .
.
Решение:
Здесь основание и показатель степени зависят от х. Логарифмируя, получим 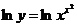 ,
, 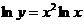 . Продифференцируем обе части последнего равенства по х. Так как у является функцией от х, то
. Продифференцируем обе части последнего равенства по х. Так как у является функцией от х, то 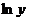 есть сложная функция х и
есть сложная функция х и 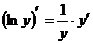 . Следовательно,
. Следовательно,
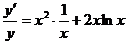 ,
,
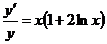 , т.е.
, т.е.
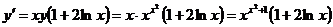 .
.
Ответ: 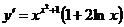
Дифференцирование неявных функций.
Пример 9. Найти производную 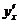 из уравнения
из уравнения 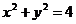 .
.
Решение:
Так как у является функцией от х, то будем рассматривать у2 как сложную функцию от х. Следовательно,  .
.
Продифференцировав по х обе части данного уравнения, получим 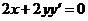 , т.е.
, т.е. 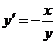 .
.
Ответ: 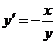 .
.
Пример 10. Найти производную 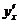 из уравнения
из уравнения 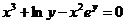 .
.
Решение:
Дифференцируя по х обе части уравнения, получаем
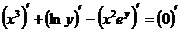
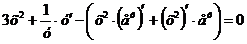
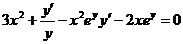
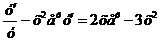
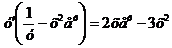
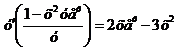
т.е. 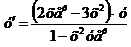 .
.
Ответ: 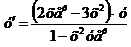 .
.
Задания для практической работы.
Вариант № 1.
Найти производные функций:
1. 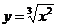 .
.
2. 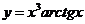 .
.
3. 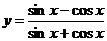 .
.
4. 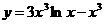 .
.
5. 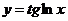 .
.
6. 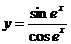 .
.
7. 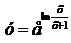 .
.
Найти производную 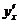 от неявных функций:
от неявных функций:
8. 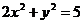 .
.
9. 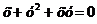 .
.
10. 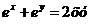 .
.
Вариант № 2.
Найти производные функций:
1. 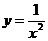 .
.
2. 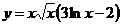 .
.
3. 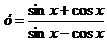 .
.
4. 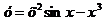 .
.
5. 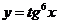 .
.
6. 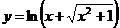 .
.
7. 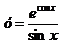 .
.
Найти производную 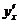 от неявных функций:
от неявных функций:
8. 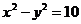 .
.
9. 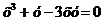 .
.
10. 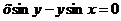 .
.
Практическая работа № 4.
Тема: Дифференциальные уравнения первого порядка.
Цели работы: познакомиться с понятием дифференциального уравнения, научиться находить общее и частное решение дифференциальных уравнений с разделяющимися переменными и линейных дифференциальных уравнений первого порядка.
Краткое изложение темы.
Уравнение вида
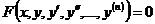 ,
,
связывающее аргумент  , неизвестную функцию
, неизвестную функцию 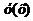 и ее производные, называется дифференциальным уравнением.
и ее производные, называется дифференциальным уравнением.
Решением дифференциального уравнения называется такая функция, которая обращает это уравнение в тождество.
Дифференциальным уравнением первого порядка называется уравнение вида
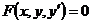
где 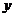 — неизвестная функция;
— неизвестная функция; 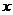 — независимая переменная.
— независимая переменная.
Общее решение уравнений имеет вид 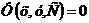 .
.
Частным решением называется решение, полученное из общего при различных числовых значениях произвольных постоянных.
Дифференциальным уравнением с разделяющимися переменными называется уравнение вида
|
|
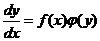 .
.
Для решения этого уравнения нужно сначала разделить переменные
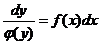 ,
,
а затем проинтегрировать обе части полученного равенства
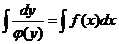 .
.
Линейным дифференциальным уравнением первого порядка называется уравнение вида
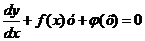 ,
,
где 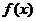 и
и 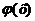 - функции от х.
- функции от х.
Это уравнение приводится к уравнению с разделяющимися переменными с помощью подстановки 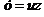 , где
, где 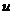 и
и 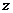 - новые функции от х.
- новые функции от х.
Примеры выполнения заданий.
1. Дифференциальные уравнения с разделяющимися переменными.
Пример 1. Найти общее решение уравнения 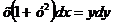 .
.
Решение:
1) Разделим переменные
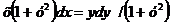 , тогда
, тогда
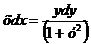
2) Интегрируем обе части полученного уравнения:
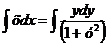 ;
;
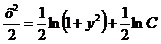 .
.
Так как произвольная постоянная С может принимать любые числовые значения, то для удобства дальнейших преобразований вместо С написали 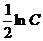 .
.
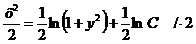
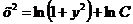
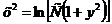
Это и есть общее решение данного уравнения.
Ответ: 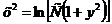 .
.
Пример 2. Найти частное решение уравнения 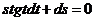 , удовлетворяющее начальным условиям
, удовлетворяющее начальным условиям 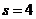 при
при 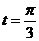 .
.
Решение:
1) Разделим переменные
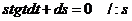
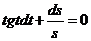
2) Интегрируем обе части полученного уравнения:
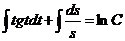
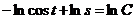
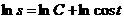
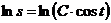
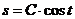 - это общее решение данного уравнения.
- это общее решение данного уравнения.
3) Для нахождения значения произвольной постоянной С подставим значения 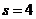 и
и 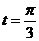 в выражение для общего решения:
в выражение для общего решения:
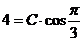 ,
,
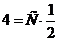 ,
,
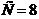 .
.
Следовательно, искомое частное решение, удовлетворяющее указанным начальным условиям, имеет вид 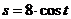 .
.
Ответ: 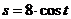 .
.
2. Линейные дифференциальные уравнения первого порядка.
Пример 3. Найти общее решение уравнения 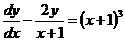 .
.
Решение:
Это линейное уравнение: здесь 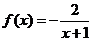 ,
, 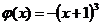 .
.
Положим 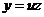 и продифференцируем это равенство по х:
и продифференцируем это равенство по х:
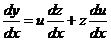 .
.
Подставив теперь выражения для 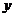 и
и 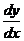 в данное уравнение, получим
в данное уравнение, получим
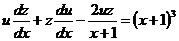 ,
,
или
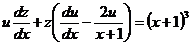 . (*)
. (*)
Так как одну из вспомогательных функций 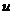 или
или 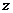 можно выбрать произвольно, то в качестве
можно выбрать произвольно, то в качестве 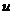 возьмем одно из частных решений уравнения
возьмем одно из частных решений уравнения 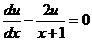 .
.
Разделим в этом уравнении переменные:
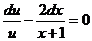
Интегрируем обе части уравнения:
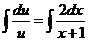 ,
,
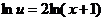 ,
,
(произвольную постоянную С принимаем равной 0, так как находим одно из частных решений)
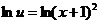 ,
,
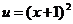 .
.
Подставим теперь выражение для 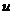 в уравнение (*); тогда получим уравнение
в уравнение (*); тогда получим уравнение
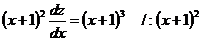
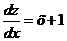 .
.
Разделим переменные
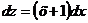
Интегрируем обе части уравнения
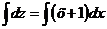
Отсюда находим
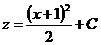
Зная 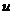 и
и 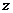 , теперь получаем общее решение данного уравнения:
, теперь получаем общее решение данного уравнения:
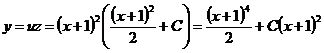 .
.
Ответ: 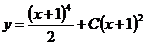 .
.
Пример 4. Найти частное решение уравнения 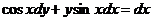 , если
, если 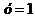 при
при 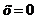 .
.
Решение:
Разделив все члены данного уравнения на 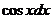 , получим уравнение
, получим уравнение
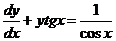 , которое является линейным.
, которое является линейным.
Положим 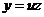 ; тогда
; тогда 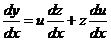 .
.
|
|
Подставив теперь выражения для 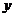 и
и 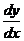 в данное уравнение, получим
в данное уравнение, получим
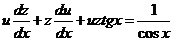 ,
,
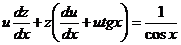 . (*)
. (*)
Для отыскания 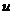 получаем уравнение
получаем уравнение
 ,
,
Разделим переменные:
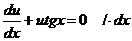
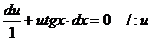
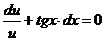
Интегрируем обе части уравнения:
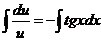 ,
,
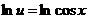 ,
,
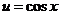 .
.
Подставляя выражение для 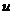 в уравнение (*), имеем
в уравнение (*), имеем
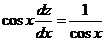 ,
,
Разделяем переменные
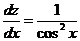 ,
,
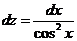 ,
,
Интегрируем обе части уравнения
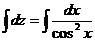 ,
,
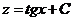 .
.
Общее решение данного уравнения:
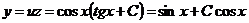 .
.
Используя начальные условия 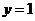 ,
,  , имеем
, имеем 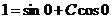 , откуда
, откуда 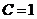 .
.
Таким образом, искомое частное решение имеет вид
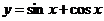 .
.
Ответ: 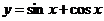 .
.
Задания для практической работы.
Вариант 1.
1. Найдите общее решение уравнения 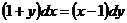 .
.
2. Найдите частное решение уравнения 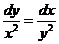 , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям 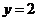 при
при  .
.
3. Найдите общее решение уравнения 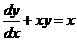 .
.
4. Найдите частное решение уравнения 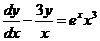 , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям 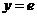 при
при 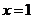 .
.
Вариант 2.
1. Найдите общее решение уравнения 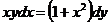 .
.
2. Найдите частное решение уравнения 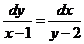 , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям 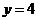 при
при  .
.
3. Найдите общее решение уравнения 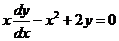 . (Приведите уравнение к общему виду линейного дифференциального уравнения первого порядка).
. (Приведите уравнение к общему виду линейного дифференциального уравнения первого порядка).
4. Найдите частное решение уравнения 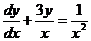 , удовлетворяющего начальным условиям
, удовлетворяющего начальным условиям 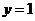 при
при 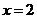 .
.
Практическая работа № 5.
|
|
|

Историки об Елизавете Петровне: Елизавета попала между двумя встречными культурными течениями, воспитывалась среди новых европейских веяний и преданий...

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим...

Организация стока поверхностных вод: Наибольшее количество влаги на земном шаре испаряется с поверхности морей и океанов (88‰)...

Биохимия спиртового брожения: Основу технологии получения пива составляет спиртовое брожение, - при котором сахар превращается...
© cyberpedia.su 2017-2024 - Не является автором материалов. Исключительное право сохранено за автором текста.
Если вы не хотите, чтобы данный материал был у нас на сайте, перейдите по ссылке: Нарушение авторских прав. Мы поможем в написании вашей работы!