Государственный Университет Управления
Институт управления
в машиностроительной промышленности
Кафедра прикладной математики
Курсовая работа по дисциплине
“Прикладная математика”
Выполнил: студент группы маш II-3,
Шерстобитов А. В.
Проверил: Онищенко А. М.
Москва, 2001
Содержание
Линейная производственная задача 3
2. Двойственная задача 5
Задача о "расшивке узких мест производства" 6
3. Транспортная задача линейного программирования 8
4. Динамическое программирование. Распределение капитальных вложений 11
5. Динамическая задача управления производством и запасами 14
6. Матричная игра как модель конкуренции и сотрудничества 16
8. Задача о кратчайшем пути 18
9. Задача о назначениях 19
14. Матричная модель производственной программы предприятия 20
15. Принятие решений в условиях неопределенности 21
16. Анализ доходности и риска финансовых операций 23
17. Задача формирования оптимального портфеля ценных бумаг 25
Двойственная задача
Ранее мы рассмотрели конкретную линейную производственную задачу по выпуску четырех видов продукции с использованием трех видов ресурсов по заданным технологиям.
Теперь представим себе, что возникла новая ситуация. Знакомый предприниматель, занимающийся производством каких-то других видов продукции, но с использованием трех таких же видов ресурсов, какие имеются у нас, предлагает нам "уступить" по определенным ценам все имеющиеся у нас ресурсы и обещает платить у1 рублей за каждую единицу первого ресурса, у2 руб – второго, у3 руб – третьего. Возникает вопрос: при каких ценах у1, у2, у3 мы можем согласиться с предложением.
Величины у1, у2, у3 принято называть расчетными, или двойственными, оценками ресурсов. Они прямо зависят от условий, в которых действует наше предприятие.
В моей задаче технологическая матрица А, вектор объемов ресурсов В и вектор удельной прибыли С имеют вид:

 4 0 8 7 316
4 0 8 7 316
A = 3 2 5 1 B= 216 C= (31 10 41 29)
5 6 3 7 199 
Для производства единицы продукции первого вида необходимо затратить, как видно из матрицы А, 4 единицы ресурса первого вида, 3 единицы ресурса второго вида и 5 единиц третьего (элементы первого столбца матрицы). В ценах у1, у2, у3 затраты составят 4у1 + 3у2 + 5у3, т.е. столько заплатит предприниматель за все ресурсы, идущие на производство единицы первой продукции. На рынке за единицу первой продукции мы получили бы прибыль 31 руб. Следовательно, мы можем согласиться с предложением П только в том случае, если он заплатит не меньше
4у1 + 3у2 + 5у3 ³ 31
Аналогично, во втором столбце матрицы А указаны затраты различных ресурсов на производство единицы продукции второго вида. Эти затраты составят 2у2 + 6у3, а на рынке за единицу продукции второго вида мы получили бы прибыль 10 рублей. Поэтому перед предпринимателем ставится условие
5у1 + 4у3 ³ 10
и так далее по всем видам продукции.
За все имеющиеся у нас ресурсы нам должны заплатить 316у1 + 216у2 + 199у3 рублей. При поставленных нами условиях предприниматель будет искать такие значения величин у1, у2, у3, чтобы эта сумма была как можно меньше. Здесь речь идет не о ценах, по которым мы когда-то приобретали эти ресурсы, а об этих ценах, которые существенно зависят от применяемых нами технологий, объемов ресурсов и от ситуации на рынке.
Таким образом, проблема определения расчетных оценок ресурсов приводит к задаче линейного программирования: найти вектор двойственных оценок
y (у1, y2, y3)
минимизирующий общую оценку всех ресурсов
W= 316y1 + 216y2 +199y3 (1)
при условии, что по каждому виду продукции суммарная оценка всех ресурсов, затрачиваемых на производство единицы продукции, не меньше прибыли, получаемой от реализации единицы этой продукции
 4у1 + 3у2 + 5у3 ³ 31
4у1 + 3у2 + 5у3 ³ 31
5у1 + 4у3 ³ 10 (2)
8у1 + 5у2 + 3у3 ³ 41
7у1 + 1у2 + 7у3 ³ 29
причем оценки ресурсов не могут быть отрицательными
y1  0, y2
0, y2  0, y3
0, y3  0 (3)
0 (3)
Решение полученной задачи легко найти с помощью второй основной теоремы двойственности, согласно которой для оптимальных решений
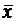 (х1, х2, х3, х4) и
(х1, х2, х3, х4) и  (y1, y2, y3)
(y1, y2, y3)
пары двойственных задач необходимо и достаточно выполнение условий
 23 (4у1 + 3у2 + 5у3 – 31) = 0
23 (4у1 + 3у2 + 5у3 – 31) = 0
0 (5у1 + 4у3 – 10) = 0
28 (8у1 + 5у2 + 3у3 – 41) = 0
0 (7у1 + 1у2 + 7у3 – 29) = 0
Так как x1 > 0 и x3 > 0, то

y1 (4*23 +8*28 - 316) = 0
y2 (3*23 +5*28 - 216) = 0
y3 (5*23 + 3*28 - 199) = 0
 4y1 + 3y2 + 5y3 = 31
4y1 + 3y2 + 5y3 = 31
8y1 + 5y2 + 3y3 = 41
y2=0
откуда следует у1=4, у3=3.
Таким образом, получили двойственные оценки ресурсов
у1=4; у2=0; у3=3, (4)
причем общая оценка всех ресурсов равна 1861.
Решение (4) содержалось в последней строке последней симплексной таблицы исходной задачи. Важен экономический смысл двойственных оценок. Например, двойственная оценка второго ресурса у1=4 показывает, что добавление одной единицы 1-го ресурса обеспечит прирост прибыли в 4 единицы.
Задача о "расшивке узких мест производства"
При выполнении оптимальной производственной программы первый и второй ресурсы используются полностью, т.е. образуют ²узкие места производства². Будем их заказывать дополнительно. Пусть T (t1, t2, t3) – вектор дополнительных объемов ресурсов. Так как мы будем использовать найденные двойственные оценки ресурсов, то должно выполняться условие:
H + Q -1T  0.
0.
Задача состоит в том, чтобы найти вектор T (t1, 0, t3), максимизирующий суммарный прирост прибыли
W = 4t1 + 3t3 (1)
при условии сохранения двойственных оценок ресурсов (и, следовательно, структуры производственной программы)
 (2)
(2)
предполагая, что можно надеяться получить дополнительно не более 1/3 первоначального объема ресурса каждого вида

 t1 316
t1 316
0 <=1/3* 216 (3)
t3 199
По смыслу задачи t1 ³ 0, t3 ³ 0
 28 + 1/28*t1 ³ 0
28 + 1/28*t1 ³ 0
7 - 4/7*t1 - 1/7*t3 ³ 0
23 –3/28*t1 + 2/7 t3 ³ 0
t1 £ 316/3
t3 £ 199/3
 t1 ³ -784
t1 ³ -784
4/7*t1 + 1/7*t3 £ 7
–3/28*t1 + 2/7 t3 ³ 23
t1 £ 316/3
t3 £ 199/3
t1 ³ 0, t3 ³0




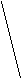


 Находим координаты точки А(t1,t2). t1 = 0, t2 =49, и прирост прибыли составляет 0*4+49*3=147 рублей.
Находим координаты точки А(t1,t2). t1 = 0, t2 =49, и прирост прибыли составляет 0*4+49*3=147 рублей.
| cj
|
|
|
|
| b
| x4+i
| yi
| ti
|
| aij
|
|
|
|
|
|
| -3/28
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 2/7
|
|
| xj
|
|
|
|
|
|
|
|
| Dj
|
|
|
|
|
|
|
|
|
Таблица 1
| xj
|
|
|
|
|
|
|
|
|
| f1 (x1)
|
|
|
|
|
|
|
|
|
| f2 (x2)
|
|
|
|
|
|
|
|
|
| f3 (x3)
|
|
|
|
|
|
|
|
|
| f4 (x4)
|
|
|
|
|
|
|
|
|
Прежде всего заполняем табл. 2. Значения f2(x2) складываем со значениями F1(x - x2) = f1(x- x2) и на каждой северо-восточной диагонали находим наибольшее число, которое отмечаем звездочкой и указываем соответствующее значение  . Заполняем таблицу 3.
. Заполняем таблицу 3.
Продолжая процесс, табулируем функции F3(x),  (x) и т.д. В табл. 6 заполняем только одну диагональ для значения x= 700. Наибольшее число на этой диагонали:
(x) и т.д. В табл. 6 заполняем только одну диагональ для значения x= 700. Наибольшее число на этой диагонали:
Zmax = 84 тыс. руб.,
причем четвертому предприятию должно быть выделено
х*4 = 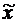 4 (700) = 0 тыс. руб.
4 (700) = 0 тыс. руб.
На долю остальных трех предприятий остается 700 тыс. руб. Из табл. 5 видно, что третьему предприятию должно быть выделено
x*3 = 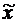 3 (700-x*4) =
3 (700-x*4) =  3 (700) = 200 тыс. руб.
3 (700) = 200 тыс. руб.
Продолжая обратный процесс, находим
x*2 =  2 (700 - x*4 - x*3) =
2 (700 - x*4 - x*3) =  2 (500) = 300 тыс. руб.
2 (500) = 300 тыс. руб.
На долю первого предприятия остается
x*1 = 700 - x*4 - x*3 - x*2 = 200 тыс. руб.
Таким образом, наилучшим является следующее распределение капитальных вложений по предприятиям:
x*1 =200; x*2 =300; x*3 = 200; x*4 = 0.
Оно обеспечивает производственному объединению наибольший воможный прирост прибыли 20 + 37 + 27 = 84 тыс. руб.
f1(x*1) + f2(x*2) + f3(x*3) + f4(x*4) = z max
Другим решением может служить распределение x*1 =100; x*2 =300; x*3 = 200; x*4 = 100. Оно получается, если в таблице 6 4-му предприятию выделить 100 тыс. руб. Прирост прибыли в этом случае составит также 84 тыс. руб (10 + 27 + 37 + 10).
 Таблица 2
Таблица 2
|
| x - x2
| 0 100 200 300 400 500 600 700
|
| x2
| F1(x - x2)
f2(x2)
| 0 10 20 30 38 43 49 52
|
 0 0
|
| 0 10 20 30 38 43 49 52
|
|
|
| 13 23 33 43 51 56 62
|
|
|
| 25 35 45 55 63 68
|
|
|
| 37 47 57 67 75
|
|
|
| 47 57 67 77
|
|
|
| 55 65 75
|
|
|
| 61 71
|
|
|
| 66.
|
Таблица 3
| x
| 0 100 200 300 400 500 600 700
|
| F2(x)
| 0 13 25 37 47 57 67 77
|
`  (x) (x)
| 0 100 200 300 300 300 300 400
|
 Таблица 4
Таблица 4
|
| x - x3
| 0 100 200 300 400 500 600 700
|
| x3
| F2(x - x3)
f3(x3)
| 0 13 25 37 47 57 67 77
|
 0 0
|
| 0 13 25 37 47 57 67 72
|
|
|
| 16 29 41 53 63 73 83
|
|
|
| 27 40 52 64 74 84
|
|
|
| 37 50 62 74 84
|
|
|
| 44 57 69 81
|
|
|
| 48 61 73
|
|
|
| 50 63
|
|
|
| 49.
|
Таблица 5
| x
| 0 100 200 300 400 500 600 700
|
| F3(x)
| 0 16 29 41 53 64 74 84
|
`  (x) (x)
| 0 100 100 100 100 200 200 200
|
Таблица 6
|
| x - x4
| 0 100 200 300 400 500 600 700
|
| x4
| F3(x - x4)
f4(x4)
| 0 16 29 41 53 64 74 84
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 41.
|
Задача о кратчайшем пути
Необходимо найти кратчайший путь между пунктами 0 и 8.
7 11
6 10 9
7 9
11 5 3




















 12 13
12 13
X0 = 0
X1 = +¥ = 3
X2 = +¥ = 6
X3 = +¥ = 12
X4 = +¥ = 13
6 + 7
3 + 11
X5 = +¥ = 15
3 + 12
X6 = +¥ = 16
7 + 12
6 + 10
X7 = +¥ = 18
13 + 5
X8 = +¥ = 21
12 + 11
16 + 9
13 + 9
13 + 5 + 3
15 + 13
Таким образом, кратчайшее расстояние между двумя пунктами 0 и 8 = 6 + 7 + 5 + 3 = 21
9. Задача о назначениях
Исходные данные предложены самостоятельно. Необходимо решить задачу о назначениях.
Проект “изготовление мебели”
X1 = 0
X2 = +¥
3 часа
 X3 = +¥
X3 = +¥
2 часа
3 часа
X4 = +¥
4 + 3 часа
X5 = +¥
7 + 5 часов
На изготовление одной единицы мебели необходимо потратить 7 + 5 = 12 часов.
Составим матрицу рисков.
Имеем q1=0;q2=16;q3=32;q4=40. Следовательно, матрица рисков есть

Принятие решений в условиях полной неопределенности.
Не все случайное можно "измерить" вероятностью. Неопределенность – более широкое понятие. Уникальные единичные случайные явления связаны с неопределенностью, массовые случайные явления обязательно допускают некоторые закономерности вероятностного характера. Ситуация полной неопределенности характеризуется отсутствием какой бы то ни было дополнительной информации.
Правило Вальда (правило крайнего пессимизма). Рассматривая  -e решение будем полагать, что на самом деле ситуация складывается самая плохая, т.е. приносящая самый малый доход
-e решение будем полагать, что на самом деле ситуация складывается самая плохая, т.е. приносящая самый малый доход  . Выберем решение
. Выберем решение  с наибольшим
с наибольшим 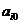 . Итак, правило Вальда рекомендует принять решение
. Итак, правило Вальда рекомендует принять решение  , такое что
, такое что 
Так, в вышеуказанном примере, имеем a1=0; a2= -6; a3=0; a4= -6. Теперь из этих чисел находим максимальное. Правило Вальда рекомендует принять 1-е или 3-е решение.
Правило Сэвиджа (правило минимального риска). При применении этого правила анализируется матрица рисков  . Рассматривая
. Рассматривая  -e решение будем полагать, что на самом деле складывается ситуация максимального риска
-e решение будем полагать, что на самом деле складывается ситуация максимального риска 
Выберем решение  с наименьшим
с наименьшим  . Итак, правило Сэвиджа рекомендует принять решение
. Итак, правило Сэвиджа рекомендует принять решение  , такое что
, такое что 
Так, имеем b1=22; b2=33; b3=0; b4=26 Теперь из этих чисел находим минимальное. Это – 0. Значит правило Сэвиджа рекомендует принять 3-е решение.
Правило Гурвица (взвешивающее пессимистический и оптимистический подходы к ситуации). Принимается решение  , на котором достигается максимум
, на котором достигается максимум
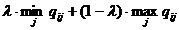
где  . Значение
. Значение  выбирается из субъективных соображений. Если
выбирается из субъективных соображений. Если  приближается к 1, то правило Гурвица приближается к правилу Вальда, при приближении
приближается к 1, то правило Гурвица приближается к правилу Вальда, при приближении  к 0, правило Гурвица приближается к правилу "розового оптимизма". При
к 0, правило Гурвица приближается к правилу "розового оптимизма". При  правило Гурвица рекомендует:
правило Гурвица рекомендует:
½(0)+1/2*22=11
½(-6)+1/2*33=13,5
½(0)+1/2*0=0
½(-6)+1/2*26=10 2-е решение.
Государственный Университет Управления
Институт управления
в машиностроительной промышленности
Кафедра прикладной математики
Курсовая работа по дисциплине
“Прикладная математика”
Выполнил: студент группы маш II-3,
Шерстобитов А. В.
Проверил: Онищенко А. М.
Москва, 2001
Содержание
Линейная производственная задача 3
2. Двойственная задача 5
Задача о "расшивке узких мест производства" 6
3. Транспортная задача линейного программирования 8
4. Динамическое программирование. Распределение капитальных вложений 11
5. Динамическая задача управления производством и запасами 14
6. Матричная игра как модель конкуренции и сотрудничества 16
8. Задача о кратчайшем пути 18
9. Задача о назначениях 19
14. Матричная модель производственной программы предприятия 20
15. Принятие решений в условиях неопределенности 21
16. Анализ доходности и риска финансовых операций 23
17. Задача формирования оптимального портфеля ценных бумаг 25




 4 0 8 7 316
4 0 8 7 316
 4у1 + 3у2 + 5у3 ³ 31
4у1 + 3у2 + 5у3 ³ 31 0, y2
0, y2  (х1, х2, х3, х4) и
(х1, х2, х3, х4) и  (y1, y2, y3)
(y1, y2, y3) 23 (4у1 + 3у2 + 5у3 – 31) = 0
23 (4у1 + 3у2 + 5у3 – 31) = 0
 4y1 + 3y2 + 5y3 = 31
4y1 + 3y2 + 5y3 = 31 (2)
(2)
 t1 316
t1 316 28 + 1/28*t1 ³ 0
28 + 1/28*t1 ³ 0 t1 ³ -784
t1 ³ -784





 Находим координаты точки А(t1,t2). t1 = 0, t2 =49, и прирост прибыли составляет 0*4+49*3=147 рублей.
Находим координаты точки А(t1,t2). t1 = 0, t2 =49, и прирост прибыли составляет 0*4+49*3=147 рублей. . Заполняем таблицу 3.
. Заполняем таблицу 3. (x) и т.д. В табл. 6 заполняем только одну диагональ для значения x= 700. Наибольшее число на этой диагонали:
(x) и т.д. В табл. 6 заполняем только одну диагональ для значения x= 700. Наибольшее число на этой диагонали: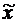 4 (700) = 0 тыс. руб.
4 (700) = 0 тыс. руб. Таблица 2
Таблица 2 0
0
 (x)
(x)





















 12 13
12 13


 X3 = +¥
X3 = +¥
 -e решение будем полагать, что на самом деле ситуация складывается самая плохая, т.е. приносящая самый малый доход
-e решение будем полагать, что на самом деле ситуация складывается самая плохая, т.е. приносящая самый малый доход  . Выберем решение
. Выберем решение  с наибольшим
с наибольшим 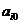 . Итак, правило Вальда рекомендует принять решение
. Итак, правило Вальда рекомендует принять решение 
 . Рассматривая
. Рассматривая 
 . Итак, правило Сэвиджа рекомендует принять решение
. Итак, правило Сэвиджа рекомендует принять решение 
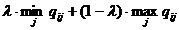
 . Значение
. Значение  выбирается из субъективных соображений. Если
выбирается из субъективных соображений. Если  правило Гурвица рекомендует:
правило Гурвица рекомендует:


