ГЛАВА II. ОСНОВЫ ЛИНЕЙНОЙ АЛГЕБРЫ
Векторы. Декартова система координат
Понятие вектора.
Определение 1. Вектором называется направленный отрезок  с начальной точкой А и конечной точкой В, который можно передвигать параллельно самому себе.
с начальной точкой А и конечной точкой В, который можно передвигать параллельно самому себе.
Определение 2. Длиной  =| а | вектора
=| а | вектора  = а называется неотрицательное число, равное длине отрезка АВ, соединяющего точки А и В. Будем также писать
= а называется неотрицательное число, равное длине отрезка АВ, соединяющего точки А и В. Будем также писать  =
=  .
.

| Таким образом, считается, что два направленных отрезка  и и  , имеющие равные длины ( , имеющие равные длины ( = =  ) и одно и то же направление, определяют один и тот же вектор а, и в этом смысле пишут а = ) и одно и то же направление, определяют один и тот же вектор а, и в этом смысле пишут а =  = =  (рис. 1).
Определение 3. Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными. (рис. 1).
Определение 3. Векторы, лежащие на одной прямой или на параллельных прямых, называются коллинеарными.
|
Определение 4. Если точки А и В совпадают, то  =
=  = 0 называется нулевым вектором. Его длина равна нулю, а направление для него не имеет смысла.
= 0 называется нулевым вектором. Его длина равна нулю, а направление для него не имеет смысла.
В геометрии рассматривают сложение и вычитание векторов, и умножение их на действительное число. По определению произведение а a=a а вектора а на число a или числа a на вектор а есть вектор, длина которого равна | a а |=| a |×| а |, а направление совпадает с а, если a> 0, или противоположно а, если a< 0. При a= 0 длина | a а | равна нулю и вектор a а превращается в нулевой вектор (точку), не имеющий направления.
Определение 5. Вектор е называется единичным, если его длина равна 1, то есть | е |=1.
Если b = a е и е – единичный вектор, то | b |=| a |, потому что
| b |=| a |×| е |=| a |×1=| a |.
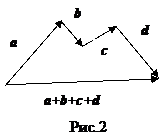
| 
| По определению векторы а, b, с,…, взятые в конечном числе, складываются по правилу замыкания цепочки этих векторов (рис. 2). На рис. 3 показано, кроме того, как вычитаются векторы.
|
Определители и их свойства
Матрицы и действия над ними
Понятие матрицы.
Определение 1. Таблица чисел аij (действительных или комплексных) вида
А=  =
=  , (1)
, (1)
состоящая из т строк и п столбцов, называется матрицей. Числа aij называются её элементами. Если т ¹ п, то матрица называется прямоугольной. При т=п она называется квадратной матрицей п -го порядка.
Определение 2. Если задана вторая матрица В= (bij) с элементами bij, тоже состоящая из т строк и п столбцов, то она считается равной матрице А тогда и только тогда, когда соответствующие элементы обеих матриц равны (aij=bij). В этом случае пишут А=В.
Необходимо помнить, что матрица  – это не число, а таблица, включающая тп чисел. Однако для квадратных матриц можно рассматривать число
– это не число, а таблица, включающая тп чисел. Однако для квадратных матриц можно рассматривать число  – определитель данной матрицы.
– определитель данной матрицы.
Определение 3. Пусть k – натуральное число, не превышающее наибольшего из чисел т и п (k£т и k£п). Зачеркнём в таблице (1) какие-либо k столбцов k строк. Элементы aij, находящиеся на пересечении зачеркнутых столбцов и строк, образуют квадратную матрицу, которая имеет определитель k -го порядка. Полученный определитель называется определителем k -го порядка, порождённым матрицей А.
Определение 4. Рангом матрицы А называется наибольшее число k, для которого существует не равный нулю определитель k -го порядка, порождаемый матрицей А.
Определение 5. Если все недиагональные элементы матрицы (т.е. все aij, у которых i ¹ j) равны нулю, то матрица называется диагональной. Если у квадратной диагональной матрицы все диагональные элементы равны единице, то матрица называется единичной. Она обозначается буквой Е:
Е=  .
.
Определение 6. Матрица (прямоугольная или квадратная) называется нулевой, если все её элементы равны нулю: aij =0 для всех i и j. Её обозначение: 0.
Определение 7. Пусть у матрицы (1) т£п. Она называется ступенчатой, если имеет следующий вид:
А=  ,
,
где аii ¹0, i =1,…, т.
2. Сумма матриц и произведение числа на матрицу. Матрицы одного и того же размера, то есть имеющие одинаковое количество строк и одинаковое количество столбцов, можно складывать.
Определение 1. Суммой двух матриц одного и того же размера А= (aij) и В= (bij) называется матрица С= (сij), элементы которой равны сумме соответствующих элементов матриц А и В: сij = aij + bij. Записывается это следующим образом:
С=А+В.
Легко видеть, что
А+В=В+А, (А+В)+ С=А+ (В+С).
Определение 2. Произведением числа l на матрицу А (или произведением матрицы А на число l) называется матрица, элементы которой равны произведениючисла l на соответствующие элементы матрицы А. Таким образом, l А=А l.
Пример 1. Пусть А=  , В=
, В=  . Найдём матрицу l А+mВ.
. Найдём матрицу l А+mВ.
n На основании определения суммы матриц и умножения матрицы на число имеем
l А=  , mВ=
, mВ=  , l А+mВ=
, l А+mВ=  . l
. l
3. Произведение матриц. Транспонированные матрицы. Произведение матриц – это специфическая операция, составляющая основу алгебры матриц. Она определена, когда число столбцов первой матрицы равно числу строк второй.
Пусть даны матрица А размером т ´ п и матрица В размером п ´ k.
Определение 1. Произведением матриц А и В называется матрица С, элементы которой сij равны сумме произведений элементов i -й строки матрицы А на соответствующие элементы j -го столбца матрицы В:
С=АВ= (сij), i= 1, …, т, j= 1, …, k. (1)
Произведение матриц А и В – матрица С – имеет размер т ´ k. Для удобства запоминания размера произведения матриц нужно перемножитьотношения размеров матриц-сомножителей: 
 =
=  , т.е. размер матрицы С равен произведению оставшихся в отношении чисел: т ´ k.
, т.е. размер матрицы С равен произведению оставшихся в отношении чисел: т ´ k.
Если А и В – прямоугольные матрицы и их произведение существует, то произведение В и А может и не существовать. Если матрицы А и В квадратные размером п ´ п, то имеет смысл как произведение матриц АВ, так и произведение матриц ВА, причем размер этих матриц такой же, как и у исходных сомножителей. При этом в общем случае перемножения матриц правило перестановочности не соблюдается, т.е. АВ ¹ ВА.
Рассмотрим примеры на умножение матриц.
Пример 1. А=  , В=
, В=  .
.
n Поскольку число столбцов матрицы А равно числу строк матрицы В, то произведение матриц АВ имеет смысл. По формулам (1) получаем в произведении матрицу размером 3´2:
АВ=  =
=  .
.
Произведение ВА не имеет смысла, так как число столбцов матрицы В не совпадает с числом строк матрицы А. l
Пример 2. А =  , В =
, В =  .
.
n Здесь мы найдем произведения данных матриц АВ и ВА:
АВ = 
 =
=  =
=  ,
,
ВА = 
 =
=  =
=  .
.
Как видно из результата, матрица произведения зависит от порядка расположения матриц в произведении. В обоих случаях произведения матриц имеют тот же размер, что и у исходных сомножителей: 2´2. l
Пример 3. А=  . Найдём матрицу А 3.
. Найдём матрицу А 3.
n Путем последовательного умножения матриц находим
А 3= А 2 А= (АА) А= 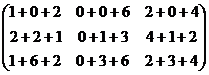
 =
=
= 
 =
=  . l
. l
Пусть А, В и С – матрицы соответствующих размеров (чтобы произведения матриц были определены), а α – действительное число. Тогда имеют место следующие свойства произведения матриц:
1. (АВ) С=А (ВС), 2. (А + В) С=AC+ВС,
3. А (В+С) =АВ+АС, 4. α (АВ) = (аА) В = А (аВ).
5. В п. 1 введено понятие единичной матрицы Е. Нетрудно убедиться, что в алгебре матриц она играет роль единицы, т.е. можно отметить еще одно свойство, связанное с умножением на эту матрицу слева и справа в случае квадратных матриц: АЕ = ЕА = А.
6. Из того, что АВ= 0 или Ап= 0 не следует, что А= 0 или В= 0. Например, А=  ¹ 0 и В=
¹ 0 и В=  ¹ 0, но, как легко проверить, АВ= 0 и А 2 = 0.
¹ 0, но, как легко проверить, АВ= 0 и А 2 = 0.
Определение 2. Если в матрице А сделать её строки столбцами с тем же номером, то получим матрицу
А Т =  ,
,
называемую транспонированной к А матрицей.
Система линейных уравнений
1. Системa из п линейных уравнений с п неизвестными.
Определение 1. Будем называть произвольную систему из п чисел  =(х 1,…, хп)Т п -мерным вектором и обозначать его х = (х 1,…, хп)Т.
=(х 1,…, хп)Т п -мерным вектором и обозначать его х = (х 1,…, хп)Т.
Зададим систему из из п линейных уравнений с п неизвестными
 (1)
(1)
Числа аuj (i, j =1,…, п) (действительные или комплексные), называемые коэффициентами системы (1), заданы. Будем ещё говорить, что система (1) определяется матрицей
А=  =
=  (2)
(2)
её коэффициентов.
Нас будет интересовать вопрос о разрешимости системы (1) для каждого вектора (столбца свободных членов) у = (y 1,…, yn)Т.
Определение 2. Вектор х = (х 1,…, хп)Т называется решением системы уравнений (1), если числа хj удовлетворяют этим уравнениям. В этом случае говорят, что система совместна. Если при этом система имеет только одно решение, то она называется определённой. Если система вообще не имеет решений, то она называется несовместной.
Определение 3. Две системы называются равносильными, или эквивалентными, если они имеют одно и то же множество решений.
Систему (1) можно записать в матричном виде
А х = у. (3)
2. Метод обратной матрицы и формулы Крамера. Вычисление определителей в MathCAD. Для получения решения системы (1) п.1 в общем виде предположим, что матрица система невырожденная, т. е. её определитель ∆=  ¹0. В этом случае существует обратная матрица А -1. Умножая слева обе части матричного уравнения (3) п.1 на матрицу А -1, получаем А -1(А х) =А -1 у. Так как
¹0. В этом случае существует обратная матрица А -1. Умножая слева обе части матричного уравнения (3) п.1 на матрицу А -1, получаем А -1(А х) =А -1 у. Так как
А -1(А х) = (А -1 А) х =Е х = х, то решением системы методом обратной матрицы будет матрица-столбец
х =А -1 у. (1)
Теорема 1 (Теорема Крамера). Пусть ∆=  – определитель матрицы А системы (1) п.1, ∆ j – определитель, получаемый из определителя ∆, если в нём заменить числа j -го столбца соответственно на числа y 1,…, yn:
– определитель матрицы А системы (1) п.1, ∆ j – определитель, получаемый из определителя ∆, если в нём заменить числа j -го столбца соответственно на числа y 1,…, yn:
∆ j=  . (2)
. (2)
Если определитель системы не равен нулю, ∆¹0, то система (1) п.1 имеет единственное решение для любого вектора у, вычисляемого по формулам (Крамера)
хj= ∆ j/ ∆ (j =1,…, п). (3)
Таким образом,
хj= 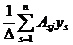 (j =1,…, п), (3¢)
(j =1,…, п), (3¢)
где Аsj – алгебраические дополнения элемента аsj в определителе ∆.
n Пусть (х 1,…, хп) есть решение системы (1) п.1. Чтобы найти неизвестное число х 1, умножим 1-е уравнение системы (1) п.1на алгебраическое дополнение А 11, второе – на А 21, …, п -е – на Ап 1 и сложим все уравнения системы. Тогда, учитывая, что
 = х 1
= х 1  = х 1∆
= х 1∆
и
 = хj
= хj  = хj ×0=0 (j ¹1),
= хj ×0=0 (j ¹1),
получаем х 1∆=∆1, где
∆1=  =
= 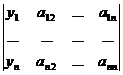 .
.
Следовательно, так как по условию ∆¹0, то х 1=∆1 / ∆.
Аналогично получаем
∆ j =  =
=  .
.
Отсюда в силу того, что ∆¹0, следует равенство (3).
Мы доказали, что если (х 1,…, хп) есть решение системы (1) п.1, то числа хj определяются равенствами (3¢).
Обратно, совокупность чисел хj= ∆ j/ ∆ (j =1,…, п) является решением системы (1) п.1. В самом деле, подставляя хj (j =1,…, п) в левую часть k – го уравнения (k =1,…, п), на основании свойств 6, 7 определителей имеем:
 =
= 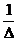
 =
= 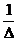
 =
= 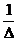 yk ∆= yk.
yk ∆= yk.
Т. о., (3¢) действительно является решением системы (1) п.1. l
Замечание. Можно показать, что если определитель системы ∆=  =0, а хотя бы один из определителей ∆ j ¹0 (j =1,…, п), то система несовместна. Если же определитель ∆=
=0, а хотя бы один из определителей ∆ j ¹0 (j =1,…, п), то система несовместна. Если же определитель ∆=  =0 и все определители ∆ j =0 (j =1,…, п), то система либо несовместна, либо имеет бесконечное количество решений.
=0 и все определители ∆ j =0 (j =1,…, п), то система либо несовместна, либо имеет бесконечное количество решений.
Пример 1. Решим систему уравнений

двумя способами: а) средствами матричного исчисления; б) по формулам Крамера.
n Исходную систему запишем в матричном виде А х = у. Здесь матрица коэффициентов А =  , х =
, х =  , у =
, у = 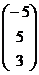 .Т.к. | А|= 7¹0 (см. пример 1 §2.3), то матрица А невырожденная, и у неё существует обратная А -1, найденная в примере 1 §2.4: А -1=
.Т.к. | А|= 7¹0 (см. пример 1 §2.3), то матрица А невырожденная, и у неё существует обратная А -1, найденная в примере 1 §2.4: А -1= 
 . Тогда по формуле (1) п.2
. Тогда по формуле (1) п.2
х =А -1 у = 

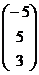 =
= 
 =
=  ,
,
т.е. х 1=1, х 2=-1, х 3=3.
б) Т.к. определитель системы | А|= 7¹0, то по теореме Крамера система имеет единственное решение: хj= ∆ j/ ∆ (j =1,…,3). Вычислим определители ∆1, ∆2 и ∆3, полученные из определителя ∆=| А| заменой соответственно 1-го, 2-го и 3-го столбцов столбцом свободных членов:
∆1=  =7, ∆2=
=7, ∆2=  =-7, ∆3=
=-7, ∆3=  =21
=21
(определители вычислены с помощью MathСAD, рис.1). Тогда по формулам Крамера (3) х 1 =  =
=  =1, х 2 =
=1, х 2 = 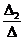 =
=  =-1, х 3 =
=-1, х 3 =  =
=  =3.
=3.
Вычисление определителей
    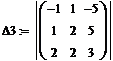 
|
| Рис.1
|
После этого рекомендуется сделать проверку, подставив найденное решение в уравнения системы и убедившись в том, что они обращаются в тождества.
3. Метод последовательного исключения неизвестных (метод Гаусса).
Определение 1. Расширенной матрицей системы (1) п.1 называется матрица А 1=  , полученная присоединением к А столбца свободных членов
, полученная присоединением к А столбца свободных членов
у =  .
.
Замечание 1. Обозначим рангматрицы А 1 через r 1 (r 1 = ранг А). Т.к. матрица А – часть А 1, то её ранг не может быть больше рангаматрицы А 1, т.е. справедливо неравенство r £ r 1.
Пусть дана система
 (1)
(1)
Определение 1. Следующие преобразования матрицы называют элементарными преобразованиями:
1) Перестановка местами любых двух строк (столбцов).
2) Умножение всех элементов любых строк (столбцов) на число k ¹0.
3) Умножение всех элементов любой строки (столбца) на постоянное число и прибавление их к соответствующим элементам другой строки (столбца).
4) Отбрасывание нулевой строки (столбца).
5) Транспонирование матрицы.
С помощью элементарных преобразований матрицы коэффициентов системы (1) п.1 получается система, равносильная данной.
Метод Гаусса заключается в том, что с помощью элементарных преобразований система уравнений приводится к системе ступенчатого вида, из которой последовательно, начиная с последних, находятся все остальные неизвестные.
Применяя подходящим образом элементарные операции над системой уравнений или, что всё равно, над расширенной матрицей  , добиться либо решения заданной системы (1), либо прийти к явно противоречивой системе. Так как последняя эквивалентна системе (1), то это докажет противоречивость системы (1).
, добиться либо решения заданной системы (1), либо прийти к явно противоречивой системе. Так как последняя эквивалентна системе (1), то это докажет противоречивость системы (1).
Ниже приводятся примеры применения этого метода.
Пример 1. Решим систему

n Конечно, согласно теореме Крамера, мы могли бы вычислить все пять определителей четвёртого порядка и найти х 1, х 2, х 3, х 4. Здесь было бы много повторяющихся вычислений.
Составим матрицу  ,
,  =
=  , где, как мы видим, последний столбец состоит из правых частей нашей системы. Умножая 1-ю строку на (-1) и прибавляя её к 3-й и 4-й строкам, получим матрицу
, где, как мы видим, последний столбец состоит из правых частей нашей системы. Умножая 1-ю строку на (-1) и прибавляя её к 3-й и 4-й строкам, получим матрицу  ~
~  . Дальнейшие преобразования матриц очевидны:
. Дальнейшие преобразования матриц очевидны:
 ~
~  ~
~  .
.
Последняя матрица эквивалентна системе

Тогда из 4-го уравнения х 4=2, из 3-го х 3=  =-3, из 2-го х 2=-2-2 х 3-3 х 4=-2, из 1-го х 1=-1-2 х 2-3 х 3-4 х 4=4. Чтобы не допустить ошибки, рекомендуется осуществить проверку, подставив полученные значения в исходные уравнения системы. l
=-3, из 2-го х 2=-2-2 х 3-3 х 4=-2, из 1-го х 1=-1-2 х 2-3 х 3-4 х 4=4. Чтобы не допустить ошибки, рекомендуется осуществить проверку, подставив полученные значения в исходные уравнения системы. l
Пример 2. Решим систему 
n Имеем:  =
= 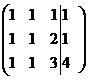 ~
~  ~
~  . Последняя строка полученной матрицы эквивалентна уравнению 0× х 1+0× х 2+0× х 3=3, что говорит о несовместности исходной системы. l
. Последняя строка полученной матрицы эквивалентна уравнению 0× х 1+0× х 2+0× х 3=3, что говорит о несовместности исходной системы. l
Пример 3. Решим систему 
n Имеем:  =
=  ~
~  ~
~  ~
~
~  . Последняя матрица эквивалентна системе
. Последняя матрица эквивалентна системе
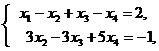
то есть система имеет бесконечное множество решений:
х 4= С 2, х 3= С 1, х 2=-  + С 1-
+ С 1-  С 2, х 1=
С 2, х 1=  -
-  С 2,
С 2,
где С 1, С 2 – любые числа (-¥< С 1, С 2<¥). l
4. Теорема Кронeкера-Капелли. Перейдём теперь к дальнейшему исследованию системы (1) п.1. Будем предполагать, что хотя бы один элемент её матрицы А не равен нулю и обозначим ранг матрицы А через r (r= ранг А). Таким образом, 1£ r £ п.
Теорема 1 (Кронeкера-Капелли). Система (1) совместна тогда и только тогда, когда ранграсширенной матрицы А 1 равен рангуматрицы А (r 1= r). В этом случае r называется рангом системы.
Теорема 2. Если ранг совместной системы равен числу неизвестных (т.е. r = п), то система является определённой. Если же r < п, то система неопределённа.
Теорема1 не означает, что для решения системы в общем случае необходимо вычислять отдельно, а затем сравнивать ранги матриц А и А 1. Для этого достаточно применить метод Гаусса для матрицы А 1. Метод Гаусса более универсален и значительно менее трудоёмок матричного метода и метода Крамера. Кроме того, метод Гаусса позволяет одновременно определить ранги матриц А и А 1 и найти решение системы, если оно существует.
Пример 1. Решим систему 
n Имеем:  =
=  ~
~  ~
~ 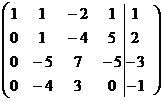 ~
~
~  ~
~  ~
~  . Ранг системы r равен 3, r =3. Матрица
. Ранг системы r равен 3, r =3. Матрица  эквивалентна системе
эквивалентна системе
 .
.
то есть система имеет бесконечное множество решений. Пусть х 4= С. Тогда
х 1=  +
+  С, х 2=-
С, х 2=-  +
+  С, х 3=-
С, х 3=-  +
+  С, х 4= С,
С, х 4= С,
где С – любое число (-¥< С <¥). l
Пример 2. Решим систему 
n Имеем:  =
= 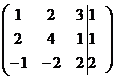 ~
~  ~
~  . При этом r (A)=2, т.к. её определитель (минор 3-го порядка) ∆= М 3=
. При этом r (A)=2, т.к. её определитель (минор 3-го порядка) ∆= М 3=  =0, а один из миноров 2-го порядка, например, М 2=
=0, а один из миноров 2-го порядка, например, М 2=  =-10¹0. Ранг же матрицы
=-10¹0. Ранг же матрицы  равен 3, т.к. её один из миноров наивысшего, 3-го порядка, например,
равен 3, т.к. её один из миноров наивысшего, 3-го порядка, например,  =-10¹0. Следовательно, по теореме Кронекера-Капелли система решений не имеет. l
=-10¹0. Следовательно, по теореме Кронекера-Капелли система решений не имеет. l
Однородная система.
Определение 1. Система уравнений
 (1)
(1)
называется однородной.
Эта система является частным случаем системы (1) п.1 при y 1=…= yт =0. Т.к. расширенная матрица А 1 однородной системыотличается от матрицы А только нулевым столбцом правых частей, то эти матрицы эквивалентны, и их ранги равны. Поэтому для однородной системы теорема Кронекера-Капелли всегда выполняется, и она совместна. Ясно, что вектор х 1=…= хп =0 удовлетворяет однородной системе (1).
Определение 2. Если однородная система (1) имеет решением ненулевой вектор х = (х 1,…, хп), то есть вектор, имеющий хотя бы одну компоненту хj ¹0, то это решение называют нетривиальным решением однородной системы (1). Нулевой вектор называют тривиальным решением однородной системы (1).
Если в системе (1) т=п, а её определитель | А |¹0, то по теореме Крамера система (1) имеет только тривиальное решение. Следовательно, нетривиальное решение возможно лишь для однородных систем, в которых число уравнений меньше числа неизвестных или при их равенстве, когда определитель системы равен нулю. Таким образом, справедлива следующая теорема:
Теорема 1. Линейная однородная система имеет нетривиальное решение тогда и только тогда, когда её ранг меньше числа неизвестных, т.е. при r (A)< n.
Пример 1. Решим однородную систему 
nИмеем: А =  ~
~  ~
~  ~
~  . Ранг матрицы A равен 2, т.к. её один из миноров наивысшего, 2-го порядка, например,
. Ранг матрицы A равен 2, т.к. её один из миноров наивысшего, 2-го порядка, например,  =-5¹0. Т.о., ранг меньше числа неизвестных, и система имеет нетривиальное решение. Последняя матрица эквивалентна системе
=-5¹0. Т.о., ранг меньше числа неизвестных, и система имеет нетривиальное решение. Последняя матрица эквивалентна системе

то есть система имеет бесконечное множество решений. Пусть х 3= С. Тогда
х 1=- С, х 2= С, х 3= С,
где С – любое число (-¥< С <¥). l
6. Нахождение ранга матрицы методом Гаусса. Следующие примеры иллюстрируют этот метод.
Пример 1. Найдём ранг матрицы  =
=  .
.
n Ясно, что ранг матрицы  не больше 4 – минимального из её размеров. В данном случае а 11=1¹0. Умножая 1-ю строку на (-1) и прибавляя её к 3-й строке, получаем: А ~
не больше 4 – минимального из её размеров. В данном случае а 11=1¹0. Умножая 1-ю строку на (-1) и прибавляя её к 3-й строке, получаем: А ~ 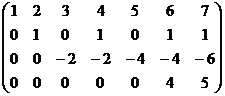 . Теперь, умножая 1-й столбец на соответствующие числа и прибавляя его к остальным столбцам, получим:
. Теперь, умножая 1-й столбец на соответствующие числа и прибавляя его к остальным столбцам, получим:
А ~  .
.
Второй столбец уже состоит из нулей, кроме элемента а 22=1¹0. Умножая 2-й столбец на (-1) и прибавляя его к 4, 6, 7 столбцам, получим
А ~  ~
~  ~
~  ~
~
~  ~
~  .
.
Определитель 4-го порядка последней матрицы не равен нулю, следовательно, её ранг, также как и ранг исходной матрицы, равен 4. l
| В MathCAD ранг матрицы вычисляется с помощью функции rank (рис.1):
|    Рис.1
Рис.1
|
Пример 2. Найдём ранг матрицы  =
=  .
.
n  ~
~  ~
~  ~
~ 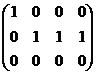 ~
~  ~
~
~ 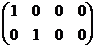 ~
~  ,
,
то есть ранг матрицы  равен 2. l
равен 2. l
Рассуждения в примерах 1 и 2 основаны на следующем общем утверждении: при элементарном преобразовании А ~ А¢ ранг матрицы сохраняется, то есть выполняется равенство r (А)= r (А ¢).
ГЛАВА II. ОСНОВЫ ЛИНЕЙНОЙ АЛГЕБРЫ



 с начальной точкой А и конечной точкой В, который можно передвигать параллельно самому себе.
с начальной точкой А и конечной точкой В, который можно передвигать параллельно самому себе. =| а | вектора
=| а | вектора  .
.
 , имеющие равные длины (
, имеющие равные длины ( ) и одно и то же направление, определяют один и тот же вектор а, и в этом смысле пишут а =
) и одно и то же направление, определяют один и тот же вектор а, и в этом смысле пишут а =  = 0 называется нулевым вектором. Его длина равна нулю, а направление для него не имеет смысла.
= 0 называется нулевым вектором. Его длина равна нулю, а направление для него не имеет смысла.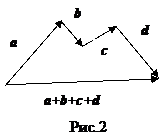

 =
=  , (1)
, (1) – определитель данной матрицы.
– определитель данной матрицы. .
. ,
, , В=
, В=  . Найдём матрицу l А+mВ.
. Найдём матрицу l А+mВ. , mВ=
, mВ=  , l А+mВ=
, l А+mВ=  . l
. l
 =
=  , т.е. размер матрицы С равен произведению оставшихся в отношении чисел: т ´ k.
, т.е. размер матрицы С равен произведению оставшихся в отношении чисел: т ´ k. , В=
, В=  .
. =
=  .
. , В =
, В =  .
. =
=  ,
, =
=  .
. . Найдём матрицу А 3.
. Найдём матрицу А 3.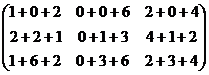

 . l
. l ¹ 0 и В=
¹ 0 и В=  ¹ 0, но, как легко проверить, АВ= 0 и А 2 = 0.
¹ 0, но, как легко проверить, АВ= 0 и А 2 = 0. ,
, =(х 1,…, хп)Т п -мерным вектором и обозначать его х = (х 1,…, хп)Т.
=(х 1,…, хп)Т п -мерным вектором и обозначать его х = (х 1,…, хп)Т. (1)
(1) (2)
(2) ¹0. В этом случае существует обратная матрица А -1. Умножая слева обе части матричного уравнения (3) п.1 на матрицу А -1, получаем А -1(А х) =А -1 у. Так как
¹0. В этом случае существует обратная матрица А -1. Умножая слева обе части матричного уравнения (3) п.1 на матрицу А -1, получаем А -1(А х) =А -1 у. Так как . (2)
. (2)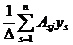 (j =1,…, п), (3¢)
(j =1,…, п), (3¢) = х 1
= х 1  = х 1∆
= х 1∆ = хj
= хj  = хj ×0=0 (j ¹1),
= хj ×0=0 (j ¹1), =
= 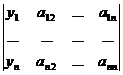 .
. =
=  =
= 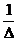
 =
=  =
= 
 , х =
, х =  , у =
, у = 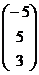 .Т.к. | А|= 7¹0 (см. пример 1 §2.3), то матрица А невырожденная, и у неё существует обратная А -1, найденная в примере 1 §2.4: А -1=
.Т.к. | А|= 7¹0 (см. пример 1 §2.3), то матрица А невырожденная, и у неё существует обратная А -1, найденная в примере 1 §2.4: А -1= 
 . Тогда по формуле (1) п.2
. Тогда по формуле (1) п.2 =
=  ,
, =7, ∆2=
=7, ∆2=  =-7, ∆3=
=-7, ∆3=  =21
=21 =
=  =1, х 2 =
=1, х 2 = 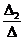 =
=  =-1, х 3 =
=-1, х 3 =  =
=  =3.
=3.



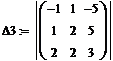

 , полученная присоединением к А столбца свободных членов
, полученная присоединением к А столбца свободных членов .
. (1)
(1) , добиться либо решения заданной системы (1), либо прийти к явно противоречивой системе. Так как последняя эквивалентна системе (1), то это докажет противоречивость системы (1).
, добиться либо решения заданной системы (1), либо прийти к явно противоречивой системе. Так как последняя эквивалентна системе (1), то это докажет противоречивость системы (1).
 , где, как мы видим, последний столбец состоит из правых частей нашей системы. Умножая 1-ю строку на (-1) и прибавляя её к 3-й и 4-й строкам, получим матрицу
, где, как мы видим, последний столбец состоит из правых частей нашей системы. Умножая 1-ю строку на (-1) и прибавляя её к 3-й и 4-й строкам, получим матрицу  . Дальнейшие преобразования матриц очевидны:
. Дальнейшие преобразования матриц очевидны: ~
~  .
.
 =-3, из 2-го х 2=-2-2 х 3-3 х 4=-2, из 1-го х 1=-1-2 х 2-3 х 3-4 х 4=4. Чтобы не допустить ошибки, рекомендуется осуществить проверку, подставив полученные значения в исходные уравнения системы. l
=-3, из 2-го х 2=-2-2 х 3-3 х 4=-2, из 1-го х 1=-1-2 х 2-3 х 3-4 х 4=4. Чтобы не допустить ошибки, рекомендуется осуществить проверку, подставив полученные значения в исходные уравнения системы. l
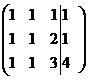 ~
~  ~
~  . Последняя строка полученной матрицы эквивалентна уравнению 0× х 1+0× х 2+0× х 3=3, что говорит о несовместности исходной системы. l
. Последняя строка полученной матрицы эквивалентна уравнению 0× х 1+0× х 2+0× х 3=3, что говорит о несовместности исходной системы. l
 ~
~  ~
~  ~
~ . Последняя матрица эквивалентна системе
. Последняя матрица эквивалентна системе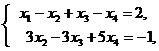
 + С 1-
+ С 1-  С 2, х 1=
С 2, х 1=  С 2,
С 2,
 ~
~  ~
~ 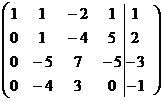 ~
~ ~
~  ~
~  . Ранг системы r равен 3, r =3. Матрица
. Ранг системы r равен 3, r =3. Матрица  .
. +
+  С, х 2=-
С, х 2=-  +
+  С, х 3=-
С, х 3=-  +
+  С, х 4= С,
С, х 4= С,
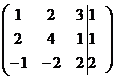 ~
~  ~
~  . При этом r (A)=2, т.к. её определитель (минор 3-го порядка) ∆= М 3=
. При этом r (A)=2, т.к. её определитель (минор 3-го порядка) ∆= М 3=  =0, а один из миноров 2-го порядка, например, М 2=
=0, а один из миноров 2-го порядка, например, М 2=  =-10¹0. Ранг же матрицы
=-10¹0. Ранг же матрицы  =-10¹0. Следовательно, по теореме Кронекера-Капелли система решений не имеет. l
=-10¹0. Следовательно, по теореме Кронекера-Капелли система решений не имеет. l (1)
(1)
 ~
~  ~
~  ~
~  . Ранг матрицы A равен 2, т.к. её один из миноров наивысшего, 2-го порядка, например,
. Ранг матрицы A равен 2, т.к. её один из миноров наивысшего, 2-го порядка, например,  =-5¹0. Т.о., ранг меньше числа неизвестных, и система имеет нетривиальное решение. Последняя матрица эквивалентна системе
=-5¹0. Т.о., ранг меньше числа неизвестных, и система имеет нетривиальное решение. Последняя матрица эквивалентна системе
 =
=  .
.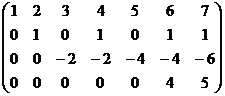 . Теперь, умножая 1-й столбец на соответствующие числа и прибавляя его к остальным столбцам, получим:
. Теперь, умножая 1-й столбец на соответствующие числа и прибавляя его к остальным столбцам, получим: .
. ~
~  ~
~  ~
~ ~
~  .
.

 Рис.1
Рис.1
 .
. ~
~  ~
~ 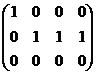 ~
~  ~
~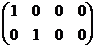 ~
~  ,
,