1. Модель Леонтьева многоотраслевой экономики (балансовый анализ). Макроэкономика функционирования многоотраслевого производства требует баланса между отраслями. С одной стороны, каждая отрасль выступает как производитель некоторой продукции, а с другой – как потребитель продукции и своей, и произведенной другими отраслями Цель балансового анализа – ответить на вопрос, возникающий в макроэкономике и связанный с эффективностью ведения многоотраслевого хозяйства: каким должен быть объем производства каждой из п отраслей, чтобы удовлетворить все потребности в продукции этой отрасли?
Связь между отраслями, как правило, отражается в таблицах межотраслевого баланса, а математическая модель, позволяющая их анализировать, разработана в 1936 г. американским экономистом В.Леонтьевым.
Предположим, что производственная сфера хозяйства представляет собой п отраслей, каждая из которых производит свою однородную продукцию. Часть продукции идет на внутрипроизводственное потребление данной отраслью и другими отраслями, а другая часть предназначена для целей конечного (вне сферы материального производства) личного и общественного потребления.
Рассмотрим процесс производства за некоторый период времени (например, год).
Введём следующие обозначения:
хi – общий (валовый) объём продукции i -й отрасли (i =1,2,…, п);
zij – объём продукции i -й отрасли, потребляемой j -й отраслью в процессе производства объёма продукции хj (i, j =1,2,…, п);
уi – объём конечного продукта i -й отрасли для потребления в непроизводственной сфере (так называемый продукт конечного потребления). Это личное потребление граждан, содержание государственных институтов и т. д.
Так как валовой объем продукции любой i -й отрасли равен суммарному объему продукции, потребляемой п отраслями, и конечного продукта, то
хi=  +уi, (i =1,2,…, п). (1)
+уi, (i =1,2,…, п). (1)
Уравнения (1) называются соотношениями баланса. Т.к. продукция разных отраслей имеет разные измерения, будем в дальнейшем рассматривать стоимостный межотраслевой баланс, когда все величины, входящие в (1), имеют стоимостное выражение.
Введем коэффициенты прямых затрат
аij=  , (i, j =1,2,…, п), (2)
, (i, j =1,2,…, п), (2)
показывающие затраты продукции i -й отрасли на производство единицы продукции j -й отрасли.
Можно полагать, что в некотором промежутке времени коэффициенты аij будут постоянными и зависящими от сложившейся технологии производства. Это означает линейную зависимость материальных затрат от валового выпуска, т.е.
zij=аijхj, (i, j=1,2,…,п), (3)
вследствие чего построенная на этом основании модель межотраслевого баланса получила название линейной. Теперь соотношения баланса (1) примут вид:
хi=  +уi, (i=1,2,…,п). (4)
+уi, (i=1,2,…,п). (4)
Обозначим x =  , А=
, А=  , y =
, y =  ,
,
где x – вектор валового выпуска, y – вектор конечного продукта, А – матрица прямых затрат (технологическая или структурная матрица).
Тогда систему (1) можно записать в матричном виде:
x =А x + y. (5)
Уравнение межотраслевого баланса можно использовать в двух целях. В первом, наиболее простом случае, когда известен вектор валового выпуска Х, требуется рассчитать вектор конечного продукта Y.
Во втором случае уравнение межотраслевого баланса используется для целей планирования: для периода времени Т (например, год) известен вектор y конечного продукта (потребления) и требуется определить вектор x валового выпуска. Тогда необходимо решать систему линейных уравнений с известной матрицей А и заданным вектором y. Эта задача является основной задачей межотраслевого баланса .
Перепишем уравнение (4) в виде:
(Е-А) x = y. (6)
Если матрица (Е-А) невырожденная, т.е. |Е-А| ¹0, то по формуле (4) §4.2
x = (Е-А)-1 y. (7)
Матрица S =(Е-А)-1 называется матрицей полных затрат. Чтобы выяснить экономический смысл элементов матрицы S= (sij), будем задаваться единичными векторами конечного продукта y ( 1)=(1,0,...,0)Т, y ( 2 ) =(0,1,...,0)Т, …, y ( п )=(0,0,...,1)Т. Тогда по (7) соответствующие векторы валового выпуска будут
x ( 1)=(s 11, s 21,..., sп 1)Т, x ( 2 ) =(s 12, s 22,..., sп 2)Т, …, x ( п )=(s 1 п, s 2 п,..., sпп)Т.
Следовательно, каждый элемент sij матрицы S есть величина валового выпуска продукции i -й отрасли, необходимого для обеспечения выпуска единицы конечного продукта j -й отрасли уj= 1 (j =1,2,..., п).
В соответствии с экономическим смыслом задачизначения хi должны быть неотрицательны при неотрицательных значениях уj и aij, где i,j= 1,2,.. .,п.
Определение. Матрица А с неотрицательными элементами называется продуктивной, если длялюбого вектора y с неотрицательными элементами существует решение x уравнения (5)с неотрицательными элементами. В этомслучае и модель Леонтьева называется продуктивной.
Существует несколько критериев продуктивности матрицы А. Один из них говорит о том, что матрица А продуктивна, если максимум сумм элементов ее столбцов не превосходит единицы, причем хотя бы для одного из столбцов сумма элементов строго меньше единицы, т.е. матрица А продуктивна, если aij ³0для любых i,j= 1,2 ,..., п и 
 £l, и существует номер j такой, что
£l, и существует номер j такой, что  < 1.
< 1.
2. Линейная модель торговли. Одним из примеров экономического процесса, приводящего к понятию собственного числа и собственного вектора матрицы, является процесс взаимных закупок товаров. Будем полагать, что бюджеты п стран, которые мы обозначим соответственно х 1, х 2, …, хn, расходуются на покупку товаров. Мы будем рассматривать линейную модель обмена, или, как ее еще называют, модель международной торговли.
Пусть aij – доля бюджета хj, которую j- я страна тратит на закупку товаров у i -й страны. Введем матрицу коэффициентов аij:
А=  (1)
(1)
Тогда если весь бюджет расходуется только на закупки внутри страны и вне ее (можно это трактовать как торговый бюджет), то справедливо равенство
 =1 (2)
=1 (2)
Матрица (1) со свойством (2), в силу которого сумма элементов ее любого столбца равна единице, называется структурной матрицей торговли. Для i -й страны общая выручка от внутренней и внешней торговли выражается формулой Pi=аi 1 x 1+ аi 2 x 2+…+ аinxn. Условие сбалансированной (бездефицитной) торговли формулируется естественным образом: для каждой страны ее бюджет должен быть не больше выручки от торговли, т.е. Pi ³ xi, или
аi1x1+аi2x2+…+аinxn³xi, i=1,2,..., п. (3)
Докажем, что в условиях (3) не может быть знака неравенства. Действительно, сложим все эти неравенства при i от 1 до п. Группируя слагаемые с величинами бюджетов xj, получаем
x 1(a 11+ a 21+…+ an 1)+ х 2(а 12 +а 22+…+ an 2)+...+ xn (a 1 n + а 2 n +…+ апп)³ x 1 +x 2 +...+xп.
Нетрудно видеть, что в скобках стоят суммы элементов матрицы А по ее столбцам от первого до последнего, которые равны единице по условию (2). Стало быть, мы получили неравенство x 1 +x 2 +...+xп³x 1 +x 2 +...+xп, откуда возможен только знак равенства.
Таким образом, условия (3) принимают вид равенств:
 (4)
(4)
Введем вектор бюджетов x, каждая компонента которого характеризует бюджет соответствующей страны; тогда систему уравнений (4) можно записать в матричной форме
А x = x. (5)
Это уравнение означает, что собственный вектор структурной матрицы А, отвечающий ее собственному значению l =1, состоит из бюджетов стран бездефицитной международной торговли.
Перепишем уравнение (5) в виде, позволяющем определить x:
(А - Е) x = 0. (6)
3. Решение примеров линейной алгебры с помощью MathCAD. Векторные и матричные операторы и функции системы MathCAD позволяют решать широкий круг задач линейной алгебры. К примеру, если заданы матрица А и вектор В для системы линейных уравнений в матричной форме Х=В, то вектор решения можно получить из выражения Х=А -1× В или с помощью встроенной функции isolve(А,B), а также с помощью символьной операции solve.
Пример 1. В таблице приведены данные об исполнении межотраслевого баланса за отчетный период, усл. ден. ед.:
| №№
| Отрасль
| Потребление
| Валовой
выпуск
|
|
|
|
|
|
|
|
| Станкостроение
Энергетика
Промышленное и с/х
машиностроение
Автомобильная промышленность
Газодобывающая промышленность
|
|
|
|
|
|
|
Вычислим:
1) Конечный продукт при данном валовом выпуске.
2) Необходимый объем валового выпуска каждой отрасли, если конечное потребление по отраслям составляет соответственно 120, 350, 70, 175 и 550 усл. ден. ед.
n Решение приведено на рис.1. Оно сопровождается комментариями, набранными с помощью команд Вставка–Текстовая область.
| 1. Определение вектора конечного продукта для непроизводственного потребления при заданном векторе валового продукта
|
 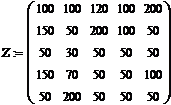  
|
Вектор валового продукта Х, его размерность n и объём продукции Z i-й отрасли, потребляемой j-й отраслью
|
   
|
Определение матрицы прямых затрат
|
     
|
Проверка продуктивности матрицы прямых затрат
|
   
|
Конечный продукта при данном объёме валового выпуска.
|
| Таким образом, конечный продукт при данном валовом выпуске и матрице прямых затрат должен быть следующим (в усл. ден. ед.):
станкостроение 380, энергетика 450, промышленное и с/х машиностроение 270,
автомобильная промышленность 80, газодобывающая промышленность 600.
|
| 2. Определение необходимого объёма валового выпуска каждой отрасли при заданном конечном потреблении
|

| Заданный вектор конечного продукта для непроизводственного потребления
|
  
|
Матричное решение системы линейных уравнений для определения необходимого вектора валового продукта Х1
|
 
| Решение системы с применением функции isolve для определения необходимого ветора валового продукта Х1
|
| Таким образом, чтобы обеспечить заданный вектор конечного продукта, необходимый валовый продукт должен быть следующим (в усл. ден. ед.):
станкостроение 1094, энергетика 1092, промышленное и с/х машиностроение 557,
автомобильная промышленность 567, газодобывающая промышленность 1143. l
|
| Рис.1
|
| | | |
Пример 2. Структурная матрица торговли четырех стран имеет вид:
А=  .
.
Найдём бюджеты этих стран для сбалансированной бездефицитной торговли.
n Решение приведено на рис. 2. При этом для решения однородной системы (6) использована символьная операция solve.
| РЕШЕНИЕ ЗАДАЧИ ЛИНЕЙНОЙ МОДЕЛИ ТОРГОВЛИ
|

| Заданная структурная матрица торговли
|
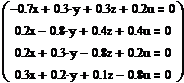 solve,x,y,z,u solve,x,y,z,u 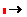 (1.222z; 1.259z; z; 0.897z) (1.222z; 1.259z; z; 0.897z)
| Решение однородной системы (А-Е)Х=0, заданной в векторной форме, с помощью символьной операции solve
|
| Здесь z может принимать любые действительные значения. Таким образом, сбалансированность торговли четырёх стран достигается при векторе национальных доходов Х=(1,22z; 1,26z; z; 0,90z), т.е. при соотношении национальных доходов примерно как 11:11,3:9:8.
|
| Рис.2 l
|



 +уi, (i =1,2,…, п). (1)
+уi, (i =1,2,…, п). (1) , (i, j =1,2,…, п), (2)
, (i, j =1,2,…, п), (2) +уi, (i=1,2,…,п). (4)
+уi, (i=1,2,…,п). (4) , А=
, А=  , y =
, y =  ,
,
 £l, и существует номер j такой, что
£l, и существует номер j такой, что  (1)
(1) (4)
(4)
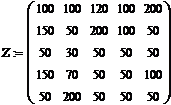




















 .
.
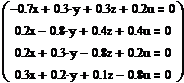 solve,x,y,z,u
solve,x,y,z,u  (1.222z; 1.259z; z; 0.897z)
(1.222z; 1.259z; z; 0.897z)



