Пусть Х(t) - марковский процесс с непрерывным временем и дискретными состояниями S1, S2,..., Sn. В дальнейшем для краткости будем его называть непрерывным марковским процессом. Обозначим  ,
,  , - вероятность того, что система, находящаяся в момент времени r в состоянии Si, окажется в момент времени t в состоянии Sj.
, - вероятность того, что система, находящаяся в момент времени r в состоянии Si, окажется в момент времени t в состоянии Sj.
Марковский процесс называется однородным, если при любых i, j, r, t вероятность  зависит только от длины интервала
зависит только от длины интервала  и не зависит от того, где он расположен на оси времени Ot.
и не зависит от того, где он расположен на оси времени Ot.
В дальнейшем будем рассматривать только однородные марковские процессы и через 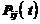 будем обозначать вероятность того, что система за время t перейдет из состояния Si в состояние Sj. Для непрерывного марковского процесса вероятность перехода из состояния Si в состояние Sj при
будем обозначать вероятность того, что система за время t перейдет из состояния Si в состояние Sj. Для непрерывного марковского процесса вероятность перехода из состояния Si в состояние Sj при  в любой момент времени равна нулю. Поэтому введем в рассмотрение
в любой момент времени равна нулю. Поэтому введем в рассмотрение  по формуле
по формуле
 , (1)
, (1)
где  называется плотностью или интенсивностью вероятности перехода из состояния Si в состояние Sj. Тогда вероятность того, что система, находящаяся в состоянии Si, за малый промежуток времени
называется плотностью или интенсивностью вероятности перехода из состояния Si в состояние Sj. Тогда вероятность того, что система, находящаяся в состоянии Si, за малый промежуток времени  перейдет в состояние Sj с точностью до бесконечно малых более высокого порядка равна
перейдет в состояние Sj с точностью до бесконечно малых более высокого порядка равна 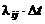 .
.
Обозначим  - вероятность того, что система в момент времени t находится в состоянии Si. Эти вероятности применяются для описания случайного процесса с дискретными состояниями. Можно показать, что если число состояний марковского процесса конечно и равно n, то вероятности
- вероятность того, что система в момент времени t находится в состоянии Si. Эти вероятности применяются для описания случайного процесса с дискретными состояниями. Можно показать, что если число состояний марковского процесса конечно и равно n, то вероятности  удовлетворяют системе дифференциальных уравнений.
удовлетворяют системе дифференциальных уравнений.
 (2)
(2)
Эти уравнения называются уравнениями Колмогорова. Чтобы система имела единственное решение, надо задать начальное состояние
 .
.
В частном случае, когда состояние системы в начальный момент времени  известно, например Sk, то
известно, например Sk, то  ,
, 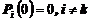 .
.
Замечание 1. Число уравнений системы (2) можно уменьшить на одно, если воспользоваться условием, что при любом t
 . (3)
. (3)
При составлении уравнений Колмогорова удобно пользоваться графом состояний системы, на котором состояния процесса изображены кружками, а возможные переходы из состояния в состояние обозначены стрелками с указанием соответствующей интенсивности.

0,8 0,2
0,4



 0,3
0,3
Рис. 1
Пример 1. Рассмотрим граф, приведенный на рисунке 1. У системы, описываемой этим марковским процессом, три состояния  , причем
, причем  ;
; 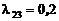 ;
;  ;
; 
 и не указываются на графе).
и не указываются на графе).
Потоком вероятности перехода из состояния Si в состояние Sj называется величина  . Уравнения Колмогорова удобно составлять по графу состояний, пользуясь правилом: производная вероятности каждого состояния равна сумме всех потоков вероятностей, идущих из других состояний в данное, минус сумма всех потоков вероятностей, идущих из данного состояния в другие. Например, для графа состояний на рис.1 получили систему уравнений
. Уравнения Колмогорова удобно составлять по графу состояний, пользуясь правилом: производная вероятности каждого состояния равна сумме всех потоков вероятностей, идущих из других состояний в данное, минус сумма всех потоков вероятностей, идущих из данного состояния в другие. Например, для графа состояний на рис.1 получили систему уравнений
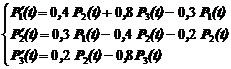 (4)
(4)
Предельный режим
Когда процесс, протекающий в системе, длится достаточно долго, возникает вопрос о значениях вероятностей  при
при  . Если существуют предельные вероятности состояний
. Если существуют предельные вероятности состояний  ,
,  то это означает, что с течением времени в системе устанавливается предельный стационарный режим, в ходе которого она переходит из одного состояния в другое, но вероятности состояний уже не меняются. В этом предельном режиме каждая предельная вероятность может быть истолкована как среднее относительное время пребывания системы в данном состоянии. Пусть число состояний конечно и равно n.
то это означает, что с течением времени в системе устанавливается предельный стационарный режим, в ходе которого она переходит из одного состояния в другое, но вероятности состояний уже не меняются. В этом предельном режиме каждая предельная вероятность может быть истолкована как среднее относительное время пребывания системы в данном состоянии. Пусть число состояний конечно и равно n.
Чтобы найти предельные вероятности состояний, надо составить систему линейных алгебраических уравнений, которая получается из уравнений Колмогорова (2), если положить в них левые части (производные) равными нулю. Затем решают полученную систему совместно с условием:
 . (5)
. (5)
Если система имеет единственное решение, то предельные вероятности состояний существуют и равны соответствующим решениям системы.
Пример 2. Найти предельные вероятности состояний системы, описываемой графом, приведенным на рис.1.
Решение.
Для этой системы по графу состояний были составлены уравнения Колмогорова (4). Положим в левых частях уравнений
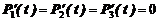 .
.
Тогда получим

Решая эту систему совместно с уравнением (5), найдем единственное решение, которое дает предельные вероятности состояний:
 ;
; 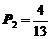 ;
;  .
.
Пример 3. В мастерской два мастера и одно место ожидания. Клиенты приходят через 10 минут и обслуживаются мастером 15 минут в среднем. Если место ожидания занято, клиент покидает мастерскую не обслуженным. Какую часть времени оба мастера заняты и какую свободны (потоки прихода и обслуживания клиентов считать пуассоновскими).
Решение.
Перечислим состояния системы: S0 -оба мастера свободны; S1 -один мастер занят, один свободен; S2 -оба мастера заняты, а место ожидания свободно; S3 -оба мастера и место ожидания заняты. Переход из состояния Si в состояние Si+1, i = 0, 1, 2..., происходит под действием потока прихода клиентов. Найдем его интенсивность  . Так как по условию среднее время между приходами двух последовательных клиентов равно 10 минут =
. Так как по условию среднее время между приходами двух последовательных клиентов равно 10 минут =  ч., то получим:
ч., то получим:  ; то есть
; то есть  . Переход из состояния S1 в состояние S0 происходит под действием потока выполнения заявок одним мастером. Его интенсивность m находится аналогично. Так как 15 минут =
. Переход из состояния S1 в состояние S0 происходит под действием потока выполнения заявок одним мастером. Его интенсивность m находится аналогично. Так как 15 минут =  ч., то
ч., то  . Переходы из состояния S2 в состояние S1 и из S3 в S2 происходят под действием потока, полученного объединением двух потоков выполнения заявок каждым из двух мастеров. Поэтому интенсивность его будет равна
. Переходы из состояния S2 в состояние S1 и из S3 в S2 происходят под действием потока, полученного объединением двух потоков выполнения заявок каждым из двух мастеров. Поэтому интенсивность его будет равна  . Интенсивности переходов из состояния Si в состояние Si-k, Si+k при
. Интенсивности переходов из состояния Si в состояние Si-k, Si+k при  , равны нулю, так как потоки ординарны, то есть события в потоках наступают «поодиночке». С учетом сказанного граф состояний будет иметь вид как на рисунке.
, равны нулю, так как потоки ординарны, то есть события в потоках наступают «поодиночке». С учетом сказанного граф состояний будет иметь вид как на рисунке.
6 6 6










4 8 8
Найдем предельные вероятности состояний Р0, Р1 , Р2 , Р3 . Для этого по графу состояний составим систему линейных уравнений Колмогорова.
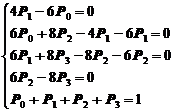
Эта система имеет единственное решение:
 ;
;  ;
;
 ;
; 
Таким образом, 22,4% времени оба мастера свободны, т.к. вероятность того, что система находится в состоянии S0 равна  .
.
Оба мастера заняты, если система находится в состоянии S2 или S3, значит вероятность этого равна  .
.
Таким образом, 44,1% времени оба мастера заняты.
СОДЕРЖАНИЕ
| 1.
| Тематический план дисциплины……………………………..
|
|
| 2.
| Рабочая программа дисциплины……………………………..
|
|
| 3.
| Список литературы (основная и дополнительная)………….
|
|
| 4.
| Контрольные вопросы для экзамена за 2 курс………………
|
|
| 5.
| Тематика контрольных работ………………………………...
|
|
| 6.
| Контрольная работа №3………………………………………
|
|
| 7.
| Методические указания по выполнению контрольной работы №3……………………………………………………..
|
|
| 8.
| Контрольная работа №4………………………………………
|
|
| 9.
| Методические указания по выполнению контрольной работы №4……………………………………………………..
|
|



 ,
,  , - вероятность того, что система, находящаяся в момент времени r в состоянии Si, окажется в момент времени t в состоянии Sj.
, - вероятность того, что система, находящаяся в момент времени r в состоянии Si, окажется в момент времени t в состоянии Sj. и не зависит от того, где он расположен на оси времени Ot.
и не зависит от того, где он расположен на оси времени Ot.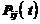 будем обозначать вероятность того, что система за время t перейдет из состояния Si в состояние Sj. Для непрерывного марковского процесса вероятность перехода из состояния Si в состояние Sj при
будем обозначать вероятность того, что система за время t перейдет из состояния Si в состояние Sj. Для непрерывного марковского процесса вероятность перехода из состояния Si в состояние Sj при  в любой момент времени равна нулю. Поэтому введем в рассмотрение
в любой момент времени равна нулю. Поэтому введем в рассмотрение  по формуле
по формуле , (1)
, (1) перейдет в состояние Sj с точностью до бесконечно малых более высокого порядка равна
перейдет в состояние Sj с точностью до бесконечно малых более высокого порядка равна 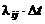 .
. - вероятность того, что система в момент времени t находится в состоянии Si. Эти вероятности применяются для описания случайного процесса с дискретными состояниями. Можно показать, что если число состояний марковского процесса конечно и равно n, то вероятности
- вероятность того, что система в момент времени t находится в состоянии Si. Эти вероятности применяются для описания случайного процесса с дискретными состояниями. Можно показать, что если число состояний марковского процесса конечно и равно n, то вероятности  (2)
(2) .
. известно, например Sk, то
известно, например Sk, то  ,
, 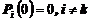 .
. . (3)
. (3)



 0,3
0,3 , причем
, причем  ;
; 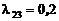 ;
;  ;
; 
 и не указываются на графе).
и не указываются на графе). . Уравнения Колмогорова удобно составлять по графу состояний, пользуясь правилом: производная вероятности каждого состояния равна сумме всех потоков вероятностей, идущих из других состояний в данное, минус сумма всех потоков вероятностей, идущих из данного состояния в другие. Например, для графа состояний на рис.1 получили систему уравнений
. Уравнения Колмогорова удобно составлять по графу состояний, пользуясь правилом: производная вероятности каждого состояния равна сумме всех потоков вероятностей, идущих из других состояний в данное, минус сумма всех потоков вероятностей, идущих из данного состояния в другие. Например, для графа состояний на рис.1 получили систему уравнений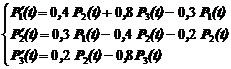 (4)
(4) . Если существуют предельные вероятности состояний
. Если существуют предельные вероятности состояний  ,
,  то это означает, что с течением времени в системе устанавливается предельный стационарный режим, в ходе которого она переходит из одного состояния в другое, но вероятности состояний уже не меняются. В этом предельном режиме каждая предельная вероятность может быть истолкована как среднее относительное время пребывания системы в данном состоянии. Пусть число состояний конечно и равно n.
то это означает, что с течением времени в системе устанавливается предельный стационарный режим, в ходе которого она переходит из одного состояния в другое, но вероятности состояний уже не меняются. В этом предельном режиме каждая предельная вероятность может быть истолкована как среднее относительное время пребывания системы в данном состоянии. Пусть число состояний конечно и равно n. . (5)
. (5)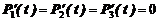 .
.
 ;
; 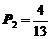 ;
;  .
. . Так как по условию среднее время между приходами двух последовательных клиентов равно 10 минут =
. Так как по условию среднее время между приходами двух последовательных клиентов равно 10 минут =  ч., то получим:
ч., то получим:  ; то есть
; то есть  . Переход из состояния S1 в состояние S0 происходит под действием потока выполнения заявок одним мастером. Его интенсивность m находится аналогично. Так как 15 минут =
. Переход из состояния S1 в состояние S0 происходит под действием потока выполнения заявок одним мастером. Его интенсивность m находится аналогично. Так как 15 минут =  ч., то
ч., то  . Переходы из состояния S2 в состояние S1 и из S3 в S2 происходят под действием потока, полученного объединением двух потоков выполнения заявок каждым из двух мастеров. Поэтому интенсивность его будет равна
. Переходы из состояния S2 в состояние S1 и из S3 в S2 происходят под действием потока, полученного объединением двух потоков выполнения заявок каждым из двух мастеров. Поэтому интенсивность его будет равна  . Интенсивности переходов из состояния Si в состояние Si-k, Si+k при
. Интенсивности переходов из состояния Si в состояние Si-k, Si+k при  , равны нулю, так как потоки ординарны, то есть события в потоках наступают «поодиночке». С учетом сказанного граф состояний будет иметь вид как на рисунке.
, равны нулю, так как потоки ординарны, то есть события в потоках наступают «поодиночке». С учетом сказанного граф состояний будет иметь вид как на рисунке.








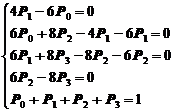
 ;
;  ;
; ;
; 
 .
. .
.


