Теорема 1. Если ограничения ЗЛП имеют допустимое решение, то они имеют и базисное решение.
Теорема 2. Базисных допустимых решений не больше, чем 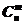 .
.
Теорема 3. Допустимая область является выпуклым множеством.
Теорема 4. Базисные допустимые решения соответствуют вершинам выпуклого множества.
Теорема 5. Все вершины выпуклого множества соответствуют базисным допустимым решениям.
Теорема 6. (Основная теорема ЗЛП). Оптимальное решение определяется допустимым базисным решением: если существует оптимальное решение ЗЛП, то существует и базисное оптимальное решение.
Если задача линейного программирования содержит только две переменные, то ее можно решить геометрическим (графоаналитическим) методом. Этот метод основан на следующих положениях.
I. Геометрически каждое решение неравенства можно представить как точку на плоскости  . Тогда множеством решений или, иначе говоря, областью решений неравенства является полуплоскость, расположенная выше или ниже прямой, описываемой уравнением
. Тогда множеством решений или, иначе говоря, областью решений неравенства является полуплоскость, расположенная выше или ниже прямой, описываемой уравнением 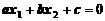 .
.
Если задана система линейных неравенств с двумя переменными:
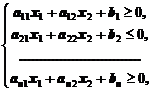
то областью решений будет служить некоторый многоугольник, образованный пересечением полуплоскостей, соответствующих области решения каждого неравенства системы.
Заметим, что область решений системы неравенств может быть и неограниченной; и пустой, когда система неравенств противоречива.
Пример 1. Найти область решений неравенства
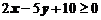 .
.
Построим прямую

на плоскости оху. Для этого найдем точки пересечения прямой с осями: имеем при 
 ; при
; при 
 .
.
Решением уравнения являются точки, принадлежащие этой прямой. Теперь рассмотрим строгое неравенство
 .
.
Для того чтобы выяснить, какая полуплоскость служит областью решения этого неравенства, решим его относительно переменной у:
 .
.
Отсюда следует, что областью решения неравенства является полуплоскость, расположенная ниже прямой (показано штрихами вниз).
Другой способ нахождения области решения неравенства заключается в использовании контрольной точки. Обычно за нее берется начало координат. Подставляя  и
и  в неравенство, получим
в неравенство, получим  . Так как полученное выражение справедливо, то точка с координатами (0,0) включается в область решения неравенства и, следовательно, искомой областью решения служит полуплоскость ниже прямой, включая и прямую.
. Так как полученное выражение справедливо, то точка с координатами (0,0) включается в область решения неравенства и, следовательно, искомой областью решения служит полуплоскость ниже прямой, включая и прямую.
II. Если задача линейного программирования имеет оптимальное решение, то линейная функция принимает оптимальное значение в одной из угловых точек многоугольника решений.
Каким образом найти эту точку покажем на примере 2.
Пример 2. Определить экстремумы функции
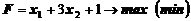
при системе ограничений:

Решение.
1. Разрешим каждое неравенство системы относительно х2; получим систему ограничений:

2. Заменим каждое неравенство системы ограничений равенством. Получим систему.


На системе 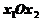 построим графики прямых системы и, учитывая знак неравенства в системе, заштрихуем соответствующую полуплоскость относительно построенной прямой.
построим графики прямых системы и, учитывая знак неравенства в системе, заштрихуем соответствующую полуплоскость относительно построенной прямой.
3. Многоугольник АВСDЕ, в котором сошлись штриховки всех полуплоскостей, образует область допустимых решений.
4. Далее на этой же системе координат построим  -вектор возрастания целевой функции
-вектор возрастания целевой функции  , и прямую F=0, то есть
, и прямую F=0, то есть  или
или  .
.
Будем перемещать F=0 параллельно самой себе в направлении вектора  (т.е. снизу вверх) до тех пор, пока прямая не выйдет из ОДР. Зафиксируем ту вершину многоугольника АВСDЕ, через которую F = 0 выходит из ОДР. Такой вершиной является С.
(т.е. снизу вверх) до тех пор, пока прямая не выйдет из ОДР. Зафиксируем ту вершину многоугольника АВСDЕ, через которую F = 0 выходит из ОДР. Такой вершиной является С.
Определим ее координаты. Для этого решим систему уравнений двух прямых, пересечением которых является точка
С 

Подставим координаты т. С (2; 4) в уравнение целевой функции F. Вычислим
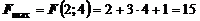 .
.
5. Чтобы определить минимум целевой функции F, построим вектор 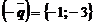 - вектор убывания F.
- вектор убывания F.
Теперь будем перемещать F=0 параллельно самой себе в направлении вектора  , то есть сверху вниз через ОДР до тех пор, пока прямая F=0 не станет выходить из ОДР. Зафиксируем ту вершину многоугольника АВСDЕ, через которую F=0 выходит из ОДР в направлении
, то есть сверху вниз через ОДР до тех пор, пока прямая F=0 не станет выходить из ОДР. Зафиксируем ту вершину многоугольника АВСDЕ, через которую F=0 выходит из ОДР в направлении 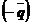 . Такой вершиной является точка А(1; 2). Подставим ее координаты (1; 2) в уравнение целевой функции F.
. Такой вершиной является точка А(1; 2). Подставим ее координаты (1; 2) в уравнение целевой функции F.
Вычислим
 .
.
Пример 3. Составить экономико-математическую модель следующей задачи.
Для выпуска изделий двух типов А и В на заводе используется сырье 4-х видов: I; II; III; IV. Расход сырья каждого вида на изготовление единицы продукции задан таблицей. Запасы сырья составляют I вида - 19 единиц; II вида - 13 единиц; III вида - 15 единиц; IV вида - 18 единиц. Выпуск одного изделия типа А приносит 7 денежных единиц, а одного изделия типа В - 5 денежных единиц.
| Виды
сырья
| Запасы
сырья
| Виды изделий
|
| А
| В
|
| I
|
|
|
|
| II
|
|
|
|
| III
|
|
|
|
| IV
|
|
|
|
| Доходы
|
|
|
Составить план производства, обеспечивающий наибольшую прибыль.
Решение.
1) Пусть  - количество изделий типа А;
- количество изделий типа А;
 - количество изделий типа В.
- количество изделий типа В.
2) Целевая функция (линейная форма), максимум которой следует определить:
 .
.
3) Система ограничений на расход сырья примет вид:

Симплексный метод
Симплексный метод является универсальным методом, которым можно решить любую задачу линейного программирования.
Идея симплекс – метода
1. Систему ограничений приводят к каноническому виду, то есть к системе m линейных уравнений с n неизвестными.
2. Находят любое ее базисное решение, по возможности наиболее простое.
3. Если первое базисное решение недопустимо, то с помощью симплекс - метода осуществляется переход к другим базисным решениям, пока не будет найдено допустимое базисное решение.
4. Если базисное решение допустимое, то проверяют его на оптимальность.
5. Если оно не оптимально, то переходят к другому допустимому базисному решению.
Симплекс - метод гарантирует на каждом шаге приближение целевой функции к оптимуму.
Таким образом, применение симплекс - метода состоит из двух этапов:
1. Нахождение допустимого базисного решения системы ограничений.
2. Нахождение оптимального решения.
Каждый этап может включать несколько шагов (итераций), соответствующих тому или иному базисному решению. Число этих шагов конечно, так как конечно число базисных решений.
Для перехода к новому базисному решению необходимо решить два вопроса:
1. Установить, какая неосновная переменная должна быть переведена в число основных.
2. Выбрать переменную, которую из основных следует перевести в неосновные на место выбывшей в основные переменные.
Ответ на первый вопрос.
Если базисное решение допустимое, а целевая функция есть функция на нахождение максимума, то берут переменную с наибольшим положительным коэффициентом и переводят ее в основные. Если целевая функция есть функция на нахождение минимума, то берут переменную с наибольшим по абсолютной величине отрицательным коэффициентом и переводят ее в основные.
Если базисное решение недопустимое, то в основные следует переводить те неосновные, которые в уравнении последней системы с отрицательным свободным членом имеют положительные коэффициенты. При этом могут представиться три случая:
1. В i -м уравнении системы уравнений нет неосновных переменных с положительными коэффициентами, то есть все коэффициенты при переменных отрицательные, как и свободный член.
В этом случае данная система ограничений - несовместна, так как она не имеет ни одного допустимого решения.
Если же нет ни одного допустимого решения системы ограничений, то нет и оптимального.
2. В i -м уравнении имеется одна переменная, коэффициент которой положителен. В этом случае в основные переводится именно эта переменная.
3. В i -м уравнении имеется несколько переменных с положительными коэффициентами. В этом случае следует определить минимальное значение для каждой из этих переменных и выбрать ту, минимальное значение которой меньше, чем у других.
Чтобы определить минимальное значение какой-либо переменной, вычисляют абсолютную величину отношения свободного члена уравнения к коэффициенту при этой переменной в этом уравнении.
Например: 
Здесь для х1 - это будет:  для х2 - это отношение будет равно ¥, так как при любом возрастании х2 переменная х3 не может стать отрицательной; для х4 - это будет
для х2 - это отношение будет равно ¥, так как при любом возрастании х2 переменная х3 не может стать отрицательной; для х4 - это будет  для х5 - это будет
для х5 - это будет  (то есть если переменная отсутствует в уравнении, то для нее отношение считают равным ¥).
(то есть если переменная отсутствует в уравнении, то для нее отношение считают равным ¥).
Таким образом, если в некоторых уравнениях знаки свободного члена и коэффициента при переменной совпадают или в каких-то уравнениях переменная, переводимая в основные, отсутствует, то отношение считают равным бесконечности, то есть ¥.
Ответ на второй вопрос.
Уравнение, из которого получено наименьшее отношение, выделяют (очерчивают рамочкой). Оно называется разрешающим.
Выделенное уравнение показывает, какая из основных переменных должна быть переведена в неосновные.
Выразив новые основные переменные через неосновные, переходят к следующему базисному решению.
Как только будет найдено допустимое базисное решение, переходят ко второму этапу симплексного метода; нахождению оптимального решения.
Правило 1. Отсутствие на каком-то шаге симплексного метода в выражении линейной формы 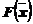 , максимум которой ищется, неосновных переменных с положительными коэффициентами, является критерием оптимальности.
, максимум которой ищется, неосновных переменных с положительными коэффициентами, является критерием оптимальности.
(Другими словами, если в выражении 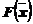 , максимум которой ищется, все переменные входят с отрицательными коэффициентами, то ее дальнейшее увеличение невозможно, то есть максимум функции достигнут).
, максимум которой ищется, все переменные входят с отрицательными коэффициентами, то ее дальнейшее увеличение невозможно, то есть максимум функции достигнут).
Правило 2. Отсутствие на каком-то шаге симплексного метода в выражении линейной формы 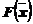 , минимум которой ищется, неосновных переменных с отрицательными коэффициентами, является критерием оптимальности. (Другими словами, если в выражении
, минимум которой ищется, неосновных переменных с отрицательными коэффициентами, является критерием оптимальности. (Другими словами, если в выражении 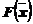 , минимум которой ищется, все переменные входят с положительными коэффициентами, то ее дальнейшее уменьшение невозможно, то есть минимум функции достигнут).
, минимум которой ищется, все переменные входят с положительными коэффициентами, то ее дальнейшее уменьшение невозможно, то есть минимум функции достигнут).
Пример 4. Для выпуска изделий двух типов А и В на заводе используется сырье 4-х видов: I; II; III; IV. Расход сырья каждого вида на изготовление единицы продукции задан таблицей. Запасы сырья составляют I вида - 19 единиц; II вида - 13 единиц; III вида - 15 единиц; IV вида - 18 единиц. Выпуск одного изделия типа А приносит 7 денежных единиц, а одного изделия типа В - 5 денежных единиц.
| Виды
сырья
| Запасы
сырья
| Виды изделий
|
| А
| В
|
| I
|
|
|
|
| II
|
|
|
|
| III
|
|
|
|
| IV
|
|
|
|
| Доходы
|
|
|
Составить план производства, обеспечивающий наибольшую прибыль.
Решение.
I. Составим экономико-математическую модель ЗЛП.
1) Пусть  - количество изделий типа А;
- количество изделий типа А;
 - количество изделий типа В.
- количество изделий типа В.
2) Система ограничений на расход сырья примет вид:
 (1)
(1)
3) Целевая функция (линейная форма), максимум которой следует определить:
 .
.
II. Приведем систему ограничений к каноническому виду, т.е. заменим неравенства равенствами, введя добавочные неотрицательные переменные х3, х4, х5, х6.
Это объемы остатков сырья каждого вида после выполнения плана по выпуску продукции. Получим систему:
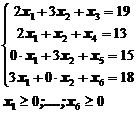
или
 (2)
(2)
Если составим минор из коэффициентов при х3, х4, х5, х6 .

то, видим, что он не равен нулю.
Значит, переменные х3, х4, х5, х6 можно принять за основные, а переменные х1 и х2 - за неосновные, то есть  .
.
Шаг 1. Основные переменные (ОП): х3; х4; х5; х6.
Неосновные переменные (НП): х1; х2.
Выразим основные переменные через неосновные.
 (3)
(3)
Базисное решение  .
.
Это базисное решение допустимо, так как все переменные неотрицательные. Подставим его в целевую функцию 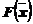 . Получим
. Получим  . Исходя из вида целевой функции, переведем в основные переменные х1, так как коэффициент 7 при х1 больше коэффициента 5 при х2.
. Исходя из вида целевой функции, переведем в основные переменные х1, так как коэффициент 7 при х1 больше коэффициента 5 при х2.
Система (3) накладывает ограничения на рост переменной х1. Так как необходимо сохранять допустимость решений, т.е. все переменные должны оставаться неотрицательными, то должны выполняться следующие неравенства (при этом переменная  как неосновная переменная):
как неосновная переменная):
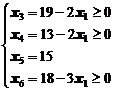 откуда следует, что
откуда следует, что  .
.
Каждое уравнение системы (3), кроме третьего, определяет оценочное отношение – границу роста переменной х1, которая должна сохранять неотрицательность соответствующей переменной.
Еще раз констатируем, что эта граница определяется абсолютной величиной отношения свободного члена уравнения к коэффициенту при х1, в этом уравнении, при условии, что эти числа имеют противоположные знаки.
Третье уравнение, в котором переменная х1 отсутствует, (или входит с нулевым коэффициентом) не ограничивает рост этой переменной. В таком случае условимся обозначать границу роста переменной символом бесконечность, т.е. ¥.
Примечание.
1) Символ ¥ будем использовать и тогда, когда знаки свободного члена и коэффициента при переменной в уравнении одинаковые, т.к. и в этом случае нет ограничений на рост переменной.
2) Если в уравнении свободный член отсутствует, точнее сказать, равен нулю, тогда а) если коэффициент при переменной отрицательный, то оценочное отношение – граница роста переменной – принимается равной нулю; б) если коэффициент при переменной положительный, то оценочное отношение – граница роста переменной – принимается равной ¥.
В нашей задаче наибольшее возможное значение для переменной х1 определяется как
 .
.
Так как меньшее значение x1 получено из последнего уравнения (его обведём рамочкой), то оно показывает, что переменную x6 следует перевести в неосновные переменные.
Вывод: Перевести x1 - в ОП; x6 - в НП.
Выразим x1 из последнего уравнения


Шаг 2. ОП: x1; x3; x4; x5;
НП: x2; x6
Выразим ОП через НП.

или
 (4)
(4)
Базисное решение (6; 0; 7; 1; 15; 0) - допустимое решение.
Подставим его в целевую функцию.
Получим
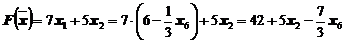 .
.
Так как коэффициент при x2 в выражении для целевой функции больше нуля, то возможно дальнейшее увеличение значения целевой функции за счёт переменной х2. Поэтому переведём в основные переменные х2. Чтобы выяснить, какую переменную из основных перевести в неосновные, определим:

Значение 1 получено из третьего уравнения системы (4).
Обведём рамочкой уравнение 3 системы (4) и переведем в НП переменную х4.
Вывод: перевести х2 - в ОП; х4 - в НП.
Выразим х2 из 3-его уравнения:
 .
.
Шаг 3. ОП: x1; x2; x3; x5;
НП: x4; x6
Выразим ОП через НП.

или
 (5)
(5)
Базисное решение (6; 1; 4; 0; 12; 0) - допустимое.
Подставим его в целевую функцию.
Получим:
 .
.
Итак,  .
.
Увеличение значения целевой функции 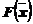 возможно за счёт переменной х6, так как она входит в
возможно за счёт переменной х6, так как она входит в 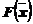 с положительным коэффициентом. Следовательно, переменную х6 переведём в ОП. Чтобы выяснить, какую переменную следует перевести в НП, определим
с положительным коэффициентом. Следовательно, переменную х6 переведём в ОП. Чтобы выяснить, какую переменную следует перевести в НП, определим
 .
.
Значение 3 получено из третьего уравнения для х3 системы (5).
Уравнение 3 системы (5) обведем рамочкой.
Вывод: Перевести х6 - в ОП;
х3 - в НП.
Выразим х6 из 3-его уравнения системы (5). Получим:
 .
.
Шаг 4. ОП: x1; x2; x5; x6;
НП: x3; x4
Выразим ОП через НП.
 . (6)
. (6)
Базисное решение (5; 3; 0; 0; 6; 3) - допустимое.
Подставим его в целевую функцию.
Получим выражение для целевой функции:
 ;
;
 .
.
Так как коэффициенты при переменных x3 и x4 отрицательные, то дальнейшее увеличение целевой функции 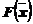 не возможно. Значит, достигнуто оптимальное значение функции
не возможно. Значит, достигнуто оптимальное значение функции 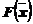 :
:  при оптимальном базисном решении (5; 3; 0; 0; 6; 3).
при оптимальном базисном решении (5; 3; 0; 0; 6; 3).
Ответ. Для получения наибольшей прибыли, равной 50 денежным единицам, из данных видов сырья завод должен изготовить 5 единиц изделий типа А, 3 единицы изделий типа В. При этом сырьё I и II видов используется полностью, а 6 единиц сырья вида III и 3 единицы сырья вида IV останутся неизрасходованными.
Пример 5. Задача о смесях (задача о диете).
При откорме животных каждое животное ежедневно должно получать не менее 6 единиц вещества К, 8 единиц вещества Z, 12 единиц вещества М. (Вещества К, Z, M могут в частности означать жиры, белки, углеводы). Для откорма животных можно закупить 3 вида кормов (например, картофель, жмых, комбикорм). Содержание единиц питательных веществ в 1 ед. каждого вида корма и стоимость 1 ед. каждого вида корма приведены в таблице.
| Вид корма
| Вещества
| Стоимость ед. корма
|
| K
| Z
| M
|
| I
|
|
|
|
|
| II
|
|
|
|
|
| III
|
| 1,5
|
| 2,5
|
| Кол-во веществ
|
|
|
|
|
Составить дневной рацион, обеспечивающий получение необходимого количества веществ при минимальных денежных затратах. (Другими словами, требуется обеспечить наиболее дешёвый рацион откорма).
Решение.
I. Составим экономико-математическую модель задачи.
1. Пусть х1 - количество единиц I вида корма,
х2 - количество единиц II вида корма,
х3 - количество единиц III вида корма.
2. Требуется определить минимум линейной формы 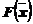 :
:

при следующих ограничениях:
 (1)
(1)
II. Вычислим оптимум функции симплексным методом
1. Введём добавочные неотрицательные переменные х4, х5, х6 и приведём систему неравенств (1) к системе уравнений (к каноническому виду) (2):

или
 (2)
(2)
2. Проще всего получить базисное решение системы (2), если за основные переменные взять добавочные переменные х4, х5, х6 (минор из коэффициентов при х4, х5, х6 отличен от 0).
Шаг 1. Основные переменные (ОП) - х4; х5; х6.
Неосновные переменные (НП) - х1; х2; х3.
Выразим ОП через НП. Получим систему уравнений (3).
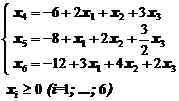 (3)
(3)
Базисное решение (0; 0; 0; -6; -8; -12) - недопустимое, так как х4, х5 и х6 - отрицательные. Чтобы определить, какую неосновную переменную перевести в основные, определим:
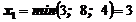 ;
;
 ;
;
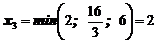 .
.
Выводы:
1) В основные переменные следует перевести х3 из 1-го уравнения системы (3) (у х3 наименьшее значение и оно получено из 1-го уравнения).
2) В неосновные переменные следует перевести х4.
Итак, 
Шаг 2. ОП х3; х5; х6.
НП х1; х2; х4.
Выразим ОП через НП. Получим систему уравнений (4).
 (4)
(4)
Базисное решение (0; 0; 2; 0; -5; -8) - недопустимое.
В основные переменные могут быть переведены или х2, или х4. Для однозначного ответа определим

 .
.
Выводы:
1) В основные переменные следует перевести х2 из 3-го уравнения системы (4). Его можно обвести рамочкой.
2) В неосновные переменные следует перевести х6.
Итак, 
Шаг 3. ОП х2; х3; х5.
НП х1; х4; х6.
Выразим ОП через НП. Получим систему уравнений (5).
 (5)
(5)
Базисное решение ( 0 ;  ) - недопустимое.
) - недопустимое.
Так как 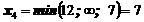 ;
;  , то из последнего уравнения системы (5) следует, что в ОП нужно перевести х6, а в НП - х5.
, то из последнего уравнения системы (5) следует, что в ОП нужно перевести х6, а в НП - х5.
Выводы:  .
.
Шаг 4. ОП х2; х3; х6.
НП х1; х4; х5.
Выразим ОП через НП. Получим систему уравнений (6).
 (6)
(6)
Базисное решение  - допустимое решение.
- допустимое решение.
Выразим целевую функцию через полученное допустимое решение, т.е. выразим
 (7)
(7)
через неосновные переменные, подставив в (7) соответствующие выражения для х2 и х3 из системы уравнений (6):

Так как все коэффициенты при переменных х1, х4, х5 - положительные, то дальнейшее уменьшение целевой функции 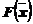 невозможно. Значит, полученное допустимое базисное решение является и оптимальным.
невозможно. Значит, полученное допустимое базисное решение является и оптимальным.
Критерий оптимальности минимума целевой функции 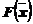 достигнут:
достигнут:
 (денежных единиц).
(денежных единиц).
Итак, чтобы обеспечить наиболее дешёвый рацион питания, нужно в основном покупать самый дорогой корм II вида; корма III вида нужно закупать почти в 4 раза меньше, а корм I вида, хотя и самый дешевый, но не выгодный.
При этом оптимальном решении будут обеспечены нормы веществ K, Z, M. К тому же вещества М на 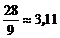 ед. окажется больше нормы.
ед. окажется больше нормы.
Алгоритм симплекс-метода
1. Задачу приводят к каноническому виду. (Введением добавочных переменных заменить неравенства равенствами).
2. Выбирают основные и неосновные переменные. В качестве основных переменных на первом шаге проще всего взять добавочные переменные.
3. Выражают основные переменные через неосновные и находят базисное решение. Если базисное решение допустимое, то переходят к п.5, если недопустимое - то к п.4.
4. От недопустимого переходят к допустимому, или устанавливают, что система несовместна.
5. Получив допустимое базисное решение, выражают через неосновные переменные этого решения целевую функцию.
Правило 1. Критерий оптимальности решения при отыскании максимума линейной функции: если в выражении линейной (целевой) функции через неосновные переменные отсутствуют положительные коэффициенты при неосновных переменных, то оптимум функции достигнут. Базисное решение, при котором достигнут оптимум, оптимальное.
Правило 2. Критерий оптимальности решения при отыскании минимума линейной функции: если в выражении линейной (целевой) функции через неосновные переменные отсутствуют отрицательные коэффициенты при неосновных переменных, то оптимум функции достигнут. Базисное решение, при котором достигнут оптимум, оптимальное.
6. Если критерий оптимальности не выполнен, то переходят к новому базисному решению.
В основные переменные переводят ту неосновную, которая входит в выражение целевой функции с наибольшим по абсолютной величине из отрицательных коэффициентов, если отыскивается минимум целевой функции F и с наибольшим положительным коэффициентом, если отыскивается максимум целевой функции F.
7. Для переменной, переводимой в основные, вычисляют абсолютную величину отношения свободного члена уравнения к коэффициенту при этой переменной в этом уравнении, если знаки свободного члена и коэффициента при переменной противоположны.
Если знаки свободного члена и коэффициента при переменной в уравнении совпадают, или коэффициент при переменной равен нулю, то отношение считают равным бесконечности (¥).
Если в уравнении свободный член отсутствует, точнее сказать, равен нулю, то
а) оценочное отношение равно нулю, если коэффициент при переменной отрицательный;
б) оценочное отношение равно ¥, если коэффициент при переменной положительный.
Из полученных значений оценочных отношений выбирают наименьшее. Уравнение, в котором получено это отношение, выделяют (очерчивают рамочкой). Оно показывает, какая основная переменная перейдет в неосновные.
8. Выражают новые основные переменные и целевую функцию через неосновные.
9. Повторяют п. 6-8 до тех пор, пока не будет достигнут критерий оптимальности. Записывают оптимальное решение и находят оптимум функции.
10. Если критерий оптимальности выполнен, а в выражении целевой функции отсутствует хотя бы одна неосновная переменная, то оптимальное решение не единственное.
11. Если в выражении линейной функции 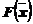 имеется неосновная переменная с положительным коэффициентом в случае ее максимизации (с отрицательным - в случае минимизации), а во все уравнения системы ограничений этого шага указанная переменная входит с положительными коэффициентами или отсутствует, то линейная функция F неограничена при данной системе ограничений. В этом случае ее максимальное (минимальное) значение записывают в виде
имеется неосновная переменная с положительным коэффициентом в случае ее максимизации (с отрицательным - в случае минимизации), а во все уравнения системы ограничений этого шага указанная переменная входит с положительными коэффициентами или отсутствует, то линейная функция F неограничена при данной системе ограничений. В этом случае ее максимальное (минимальное) значение записывают в виде  или
или 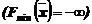 .
.
8. КОНТРОЛЬНАЯ РАБОТА №4
ВАРИАНТ 0
1. В трех хранилищах 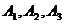 имеется соответственно 70 т., 90 т. И 50 т. топлива. Требуется спланировать перевозку топлива четырем потребителям
имеется соответственно 70 т., 90 т. И 50 т. топлива. Требуется спланировать перевозку топлива четырем потребителям  , спрос которых равен соответственно 50, 70, 40 и 70 т. так, чтобы затраты на транспортировку были минимальными, если
, спрос которых равен соответственно 50, 70, 40 и 70 т. так, чтобы затраты на транспортировку были минимальными, если
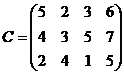 .
.
2. Полагая матрицу А во второй задаче матрицей игры с природой найти решение игры используя критерии Вальда, Сэвиджа и Гурвица (коэффициент к для критерия Гурвица положить равным 0,7).

3. В порту имеется один причал для разгрузки судов. Интенсивность потока судов равна 0,4 (судов в сутки). Среднее время разгрузки одного судна составляет 2 суток. Предполагается, что очередь может быть неограниченной длины. Найти показатели эффективности работы причала, а также вероятность того, что ожидают разгрузки не более чем 2 судна.
ВАРИАНТ 1
1. С 3-х складов 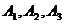 необходимо доставить овощи в 5 торговых точек
необходимо доставить овощи в 5 торговых точек  . Требуется закрепить склады за торговыми точками так, чтобы общая сумма затрат на перевозку была минимальной, если
. Требуется закрепить склады за торговыми точками так, чтобы общая сумма затрат на перевозку была минимальной, если  ;
; 

2. Полагая матрицу А во второй задаче матрицей игры с природой найти решение игры используя критерии Вальда, Сэвиджа и Гурвица (коэффициент к для критерия Гурвица положить равным 0,7).

3. Вход на станцию метрополитена оборудован системой из m=5 турникетов. При выходе из строя одного из турникетов остальные продолжают нормально функционировать. Вход на станцию перекрывается, если выйдут из строя все турникеты. Поток отказов каждого турникета – простейший, среднее время безотказной работы одного турникета t=29 часов. При выходе из строя каждый турникет начинает сразу же ремонтироваться. Время ремонта распределено по показательному закону и в среднем составляет s=4 часа. В начальный момент все турникеты исправны. Найти среднюю пропускную способность системы турникетов в процентах от номинальной, если с выходом из строя каждого турникета система теряет (100/k)% своей номинальной пропускной способности.
ВАРИАНТ 2
1. Составить план перевозки зерна из районов 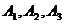 и
и  области, в которых запасы составляют соответственно 800, 700, 1000, 500 ц на три элеватора
области, в которых запасы составляют соответственно 800, 700, 1000, 500 ц на три элеватора  мощностью соответственно 1000, 1100 и 900 ц. Затраты на перевозку 1 ц. зерна из районов на элеваторы заданы матрицей:
мощностью соответственно 1000, 1100 и 900 ц. Затраты на перевозку 1 ц. зерна из районов на элеваторы заданы матрицей:
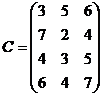
2. Полагая матрицу А во второй задаче матрицей игры с природой найти решение игры используя критерии Вальда, Сэвиджа и Гурвица (коэффициент к для критерия Гурвица положить равным 0,7).

3. АТС имеет k=4 линий связи. Поток вызова простейший с интенсивностью 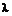 =1.4 вызовов в минуту. Среднее время переговоров составляет t =2.1 минут. Время переговоров распределено по показательному закону. Найти абсолютную и относительную пропускные способности АТС: вероятность того, что все линии связи заняты: среднее число занятых линий связи. Определить, сколько линий связи должна иметь АТС, чтобы вероятность отказа не превышала
=1.4 вызовов в минуту. Среднее время переговоров составляет t =2.1 минут. Время переговоров распределено по показательному закону. Найти абсолютную и относительную пропускные способности АТС: вероятность того, что все линии связи заняты: среднее число занятых линий связи. Определить, сколько линий связи должна иметь АТС, чтобы вероятность отказа не превышала  =0.050.
=0.050.
ВАРИАНТ 3
1. На трех хлебокомбинатах ежедневно производится 110, 190 и 90 т муки. Эта мука потребляется 4-мя хлебозаводами, ежедневные потребности которых равны соответственно 80, 60, 160, 80 т. тарифы перевозок 1 т муки с хлебокомбинатов к каждому из хлебозаводов задается матрицей:
 .
.
Составить такой план доставки муки, при котором общая стоимость затрат на перевозки была минимальной.
2. Полагая матрицу А во второй задаче матрицей игры с природой найти решение игры используя критерии Вальда, Сэвиджа и Гурвица (коэффициент к для критерия Гурвица положить равным 0,7).

3. Билетные касс



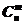 .
. . Тогда множеством решений или, иначе говоря, областью решений неравенства является полуплоскость, расположенная выше или ниже прямой, описываемой уравнением
. Тогда множеством решений или, иначе говоря, областью решений неравенства является полуплоскость, расположенная выше или ниже прямой, описываемой уравнением 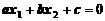 .
. 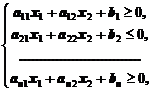
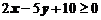 .
.


 ; при
; при 
 .
. .
. .
. . Так как полученное выражение справедливо, то точка с координатами (0,0) включается в область решения неравенства и, следовательно, искомой областью решения служит полуплоскость ниже прямой, включая и прямую.
. Так как полученное выражение справедливо, то точка с координатами (0,0) включается в область решения неравенства и, следовательно, искомой областью решения служит полуплоскость ниже прямой, включая и прямую.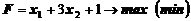




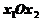 построим графики прямых системы и, учитывая знак неравенства в системе, заштрихуем соответствующую полуплоскость относительно построенной прямой.
построим графики прямых системы и, учитывая знак неравенства в системе, заштрихуем соответствующую полуплоскость относительно построенной прямой.
 -вектор возрастания целевой функции
-вектор возрастания целевой функции  , и прямую F=0, то есть
, и прямую F=0, то есть  или
или  .
. (т.е. снизу вверх) до тех пор, пока прямая не выйдет из ОДР. Зафиксируем ту вершину многоугольника АВСDЕ, через которую F = 0 выходит из ОДР. Такой вершиной является С.
(т.е. снизу вверх) до тех пор, пока прямая не выйдет из ОДР. Зафиксируем ту вершину многоугольника АВСDЕ, через которую F = 0 выходит из ОДР. Такой вершиной является С.

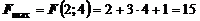 .
.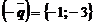 - вектор убывания F.
- вектор убывания F. , то есть сверху вниз через ОДР до тех пор, пока прямая F=0 не станет выходить из ОДР. Зафиксируем ту вершину многоугольника АВСDЕ, через которую F=0 выходит из ОДР в направлении
, то есть сверху вниз через ОДР до тех пор, пока прямая F=0 не станет выходить из ОДР. Зафиксируем ту вершину многоугольника АВСDЕ, через которую F=0 выходит из ОДР в направлении 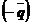 . Такой вершиной является точка А(1; 2). Подставим ее координаты (1; 2) в уравнение целевой функции F.
. Такой вершиной является точка А(1; 2). Подставим ее координаты (1; 2) в уравнение целевой функции F. .
. - количество изделий типа А;
- количество изделий типа А; - количество изделий типа В.
- количество изделий типа В. .
.

 для х2 - это отношение будет равно ¥, так как при любом возрастании х2 переменная х3 не может стать отрицательной; для х4 - это будет
для х2 - это отношение будет равно ¥, так как при любом возрастании х2 переменная х3 не может стать отрицательной; для х4 - это будет  для х5 - это будет
для х5 - это будет  (то есть если переменная отсутствует в уравнении, то для нее отношение считают равным ¥).
(то есть если переменная отсутствует в уравнении, то для нее отношение считают равным ¥).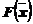 , максимум которой ищется, неосновных переменных с положительными коэффициентами, является критерием оптимальности.
, максимум которой ищется, неосновных переменных с положительными коэффициентами, является критерием оптимальности. (1)
(1) .
.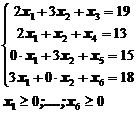
 (2)
(2)
 .
. (3)
(3) .
. . Исходя из вида целевой функции, переведем в основные переменные х1, так как коэффициент 7 при х1 больше коэффициента 5 при х2.
. Исходя из вида целевой функции, переведем в основные переменные х1, так как коэффициент 7 при х1 больше коэффициента 5 при х2. как неосновная переменная):
как неосновная переменная):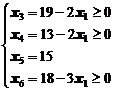 откуда следует, что
откуда следует, что  .
. .
.


 (4)
(4)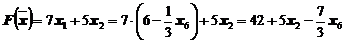 .
.
 .
.
 (5)
(5) .
. .
. .
. .
. . (6)
. (6) ;
; .
. при оптимальном базисном решении (5; 3; 0; 0; 6; 3).
при оптимальном базисном решении (5; 3; 0; 0; 6; 3).
 (1)
(1)
 (2)
(2)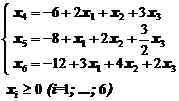 (3)
(3)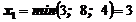 ;
; ;
;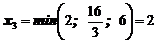 .
.
 (4)
(4)
 .
.
 (5)
(5) ) - недопустимое.
) - недопустимое.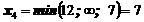 ;
;  , то из последнего уравнения системы (5) следует, что в ОП нужно перевести х6, а в НП - х5.
, то из последнего уравнения системы (5) следует, что в ОП нужно перевести х6, а в НП - х5. .
. (6)
(6) - допустимое решение.
- допустимое решение. (7)
(7)
 (денежных единиц).
(денежных единиц).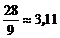 ед. окажется больше нормы.
ед. окажется больше нормы. или
или 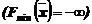 .
.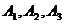 имеется соответственно 70 т., 90 т. И 50 т. топлива. Требуется спланировать перевозку топлива четырем потребителям
имеется соответственно 70 т., 90 т. И 50 т. топлива. Требуется спланировать перевозку топлива четырем потребителям  , спрос которых равен соответственно 50, 70, 40 и 70 т. так, чтобы затраты на транспортировку были минимальными, если
, спрос которых равен соответственно 50, 70, 40 и 70 т. так, чтобы затраты на транспортировку были минимальными, если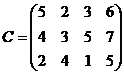 .
.
 . Требуется закрепить склады за торговыми точками так, чтобы общая сумма затрат на перевозку была минимальной, если
. Требуется закрепить склады за торговыми точками так, чтобы общая сумма затрат на перевозку была минимальной, если  ;
; 


 области, в которых запасы составляют соответственно 800, 700, 1000, 500 ц на три элеватора
области, в которых запасы составляют соответственно 800, 700, 1000, 500 ц на три элеватора  мощностью соответственно 1000, 1100 и 900 ц. Затраты на перевозку 1 ц. зерна из районов на элеваторы заданы матрицей:
мощностью соответственно 1000, 1100 и 900 ц. Затраты на перевозку 1 ц. зерна из районов на элеваторы заданы матрицей: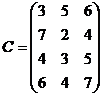

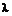 =1.4 вызовов в минуту. Среднее время переговоров составляет t =2.1 минут. Время переговоров распределено по показательному закону. Найти абсолютную и относительную пропускные способности АТС: вероятность того, что все линии связи заняты: среднее число занятых линий связи. Определить, сколько линий связи должна иметь АТС, чтобы вероятность отказа не превышала
=1.4 вызовов в минуту. Среднее время переговоров составляет t =2.1 минут. Время переговоров распределено по показательному закону. Найти абсолютную и относительную пропускные способности АТС: вероятность того, что все линии связи заняты: среднее число занятых линий связи. Определить, сколько линий связи должна иметь АТС, чтобы вероятность отказа не превышала  =0.050.
=0.050. .
.



