1. Сходящаяся последовательность имеет единственный предел.
2. Всякая подпоследовательность сходящейся последовательности сходится к тому же пределу.
3. Сходящаяся последовательность ограничена.
4. Если  , то, начиная с некоторого номера N, члены последовательности сохраняют знак а.
, то, начиная с некоторого номера N, члены последовательности сохраняют знак а.
Следствие: если  ,
,  и
и  , то, начиная с некоторого номера N выполняется неравенство
, то, начиная с некоторого номера N выполняется неравенство  .
.
5. Пусть  ,
,  , если начиная с некоторого номера N выполняется неравенство
, если начиная с некоторого номера N выполняется неравенство  , то
, то  .
.
6. Пусть для последовательностей  выполняются неравенства
выполняются неравенства  и
и  , то
, то  .
.
Теорема: если последовательности  сходятся и
сходятся и  ,
,  , то справедливы равенства:
, то справедливы равенства:
 ;
;
 ;
;
 ;
;
если  , то
, то  .
.
Монотонные последовательности
Определение. Числовая последовательность  называется неубывающей, если
называется неубывающей, если  . Последовательность называется строго возрастающей, если
. Последовательность называется строго возрастающей, если  . Аналогично, числовая последовательность
. Аналогично, числовая последовательность  называется невозрастающей, если
называется невозрастающей, если  . Последовательность называется строго убывающей, если
. Последовательность называется строго убывающей, если 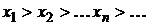 . Возрастающие и убывающие последовательности образуют класс монотонных последовательностей.
. Возрастающие и убывающие последовательности образуют класс монотонных последовательностей.
Монотонно возрастающая последовательность всегда ограничена снизу своим первым членом, а монотонно убывающая последовательность ограничена сверху своим первым членом.
Для монотонных последовательностей их ограниченность является достаточным условием сходимости.
Теорема: Если  для любого n ∊N и
для любого n ∊N и  монотонная последовательность, а также существует
монотонная последовательность, а также существует 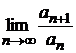 , то:
, то:
1.  ; (5.1)
; (5.1)
2.  .
.
Пример:
Найти предел последовательности  ,
,  .
.
Решение:

Очевидно, начиная с некоторого номера n, выполняется неравенство  , то есть
, то есть  . Следовательно, последовательность монотонно убывает. Так как
. Следовательно, последовательность монотонно убывает. Так как  , то согласно формуле (5.1) следует, что
, то согласно формуле (5.1) следует, что  .
.
5.4. Число е
Рассмотрим последовательность  . Согласно неравенству Бернулли,
. Согласно неравенству Бернулли,  ,
,  . Обозначим
. Обозначим  . Тогда для последовательности
. Тогда для последовательности  имеем
имеем  .
.  . Согласно неравенству Бернулли получим
. Согласно неравенству Бернулли получим  . То есть
. То есть  или последовательность
или последовательность  монотонно убывает и ограничена снизу числом 2. Следовательно, она имеет конечный предел:
монотонно убывает и ограничена снизу числом 2. Следовательно, она имеет конечный предел:
 .
.
Итак, последовательность  тоже имеет предел. Этот предел принято обозначать е:
тоже имеет предел. Этот предел принято обозначать е:

Вопросы для самоподготовки
1. Определение числовой последовательности.
2. Предел числовой последовательности.
3. Определение сходящееся последовательности.
4. Свойства сходящихся числовых последовательностей.
5. Монотонные последовательности.
6. Число е.
Введение в математический анализ
Функциональная зависимость
Понятие функции
Две физические или геометрические величины будем называть однородными, если их можно складывать по законам арифметики. При сравнении однородных величин (отвечая на вопрос во сколько раз) возникают действительные (или вещественные) числа, которые делятся на рациональные и иррациональные числа. Каждое действительное число можно изобразить точкой на числовой оси.
Действительные числа могут быть как независимые, так и зависимые. Пусть даны два непустых множества X и Y.
Определение. Говорят, что задано отображение множества Х во множество Y, или задана функция на Х со значениями в Y, если каждому элементу х ∊Х по определённому правилу f ставится в соответствие один и только один элемент у ∊Y. Это можно записать так

 ,
, 
Элемент y = f (x) называется образом элемента х при отображении f. Множество X называется областью определения функции f (x) и обозначается D(f). Множество Y – множеством значений функции f (x) и обозначается Е(f).
Элементу x из множества X может ставиться в соответствие элемент у, выбираемый случайным образом из подмножества Y1 (Y1 ∈ Y). Говорят, что между х и у существует корреляционная зависимость, если для каждого х существует определённое правило выбора подмножества Y1. Если такого правила нет, то величины х и у считаются независимыми.
Функциональную зависимость можно задать несколькими способами: в виде таблицы чисел, в виде графического рисунка, в виде условной записи функции, в виде арифметической комбинации основных элементарных функций.
Определение. Если  и
и  , то функция
, то функция  , определенная равенством F (x) = g(f (x)) называется сложной функцией.
, определенная равенством F (x) = g(f (x)) называется сложной функцией.
Определение. Если отображение  взаимно-однозначно, то для y = f (x) Î Y существует единственный прообраз x = f –1(y). Правило
взаимно-однозначно, то для y = f (x) Î Y существует единственный прообраз x = f –1(y). Правило  которое для у ÎY определяет единственный образ f –1(y) = x Î Xназывается обратной функцией или обратным отображением.
которое для у ÎY определяет единственный образ f –1(y) = x Î Xназывается обратной функцией или обратным отображением.
Частные классы отображений
В зависимости от строения множества Х и Y можно рассмотреть четыре класса отображений:
1.  y = f(x) – числовая функция одного числового аргумента, например,
y = f(x) – числовая функция одного числового аргумента, например,  и др.
и др.
2.  если
если  , то
, то  – числовая функция векторного аргумента, или числовая функция многих скалярных переменных, например,
– числовая функция векторного аргумента, или числовая функция многих скалярных переменных, например, 
3.  – вектор-функция одной переменной, ставящая в соответствие каждому вещественному числу x ÎX вектор
– вектор-функция одной переменной, ставящая в соответствие каждому вещественному числу x ÎX вектор  из
из 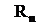 , т.е. каждая координата вектора
, т.е. каждая координата вектора  есть скалярная функция скалярного аргумента х:
есть скалярная функция скалярного аргумента х:
 .
.
Функции этого класса широко используются в физике для описания движения материальной точки М, координаты которой являются функциями времени  , что можно записать в виде
, что можно записать в виде  .
.
4.  вектор-функция векторного аргумента. Полагая
вектор-функция векторного аргумента. Полагая  , получим
, получим
 .
.
Изучение функций класса 3 и 4 сводится к изучению скалярных функций одного и многих переменных.
Примеры:
Укажите область определения функций:
1. 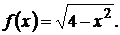
Решение: Для данной функции областью определения D(f) является множество значений переменной х, удовлетворяющих неравенству

2. 
Решение: областью определения D(f) является круг 
Определение. Множество точек  называется графиком функции
называется графиком функции  . В случае скалярной функции одного скалярного аргумента графиком функции
. В случае скалярной функции одного скалярного аргумента графиком функции  является некоторая кривая, а в случае скалярной функции двух скалярных аргументов графиком функции
является некоторая кривая, а в случае скалярной функции двух скалярных аргументов графиком функции  является некоторая поверхность. Например, графиком функции
является некоторая поверхность. Например, графиком функции  является верхняя часть сферы с центром в начале координат радиусом r = 3.
является верхняя часть сферы с центром в начале координат радиусом r = 3.
Элементарные функции
Основными элементарными функциями являются:
Степенная функция  , где α Î R. В общем случае её область определения
, где α Î R. В общем случае её область определения 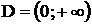 . При
. При  функция
функция  определена на всей числовой оси.
определена на всей числовой оси.
Показательная функция  , где а > 0, а ≠ 1. Её область определения – вся числовая ось.
, где а > 0, а ≠ 1. Её область определения – вся числовая ось.
Логарифмическая функция  , где а > 0, а ≠ 1. Область определения
, где а > 0, а ≠ 1. Область определения 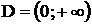 .
.
Тригонометрические функции 
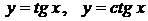 . Функции
. Функции  определены на всей числовой оси. Функция
определены на всей числовой оси. Функция  определена при
определена при 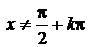 , а
, а  при
при  , где k – любое число.
, где k – любое число.
Обратные тригонометрические функции 
 y = arctg x, y = arcctg x. Областью определения функций
y = arctg x, y = arcctg x. Областью определения функций 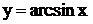 и
и  является отрезок
является отрезок 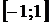 . Функции y = arctg x и y = arcctg x определены на всей числовой оси.
. Функции y = arctg x и y = arcctg x определены на всей числовой оси.
Гиперболические функции  гиперболический синус,
гиперболический синус,  гиперболический косинус (
гиперболический косинус ( натуральное число [3.4]),
натуральное число [3.4]),  гиперболический тангенс,
гиперболический тангенс, 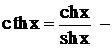 гиперболический котангенс.
гиперболический котангенс.
Предлагается самостоятельно построить графики основных элементарных функций.
Среди функций выделяют:
Функции монотонно возрастающие, если для любых  x ∊D(f) всегда
x ∊D(f) всегда  (монотонно убывающие, если для любых
(монотонно убывающие, если для любых  x ∊D(f) всегда
x ∊D(f) всегда  ).
).
Функции чётные, если для любого x ∊D(f)  (для нечётных функций
(для нечётных функций 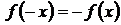 ).
).
Периодические – если существует число Т≠0, такое что для любых х,  и x + Т ∊D(f) выполняются равенства:
и x + Т ∊D(f) выполняются равенства:  . Т называется периодом.
. Т называется периодом.
Функции ограниченные сверху (снизу) – если для любого x ∊D(f)  К ∊ R (для функций ограниченных снизу
К ∊ R (для функций ограниченных снизу  ).
).
Предел функции в точке
Определение. Число А называется пределом функции f (x) при х → а, если для всякого сколь угодно малого ε > 0 найдётся такое δ(ε) > 0, что при  < δ выполняется неравенство
< δ выполняется неравенство 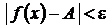 . Пишут
. Пишут
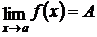 .
.
Аналогично, число А называется пределом функции f (x) при  , если для любого ε > 0 существует число М(ε) > 0 такое, что при x >M(ε) выполняется неравенство
, если для любого ε > 0 существует число М(ε) > 0 такое, что при x >M(ε) выполняется неравенство 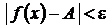 . В этом случае пишут
. В этом случае пишут
 .
.
в зависимости от нахождения х относительно а определяют левосторонний и правосторонний пределы функции. При х < а пишут
 (левосторонний предел).
(левосторонний предел).
При х > а пишут
 (правосторонний предел).
(правосторонний предел).
 Геометрическая иллюстрация определения предела функции f (x) в точке а изображена на рис. 6.1, из которого следует, что для значений х из некоторой δ-окрестности точки а соответствующие значения f (х) попадают в ε-окрестность точки А.
Геометрическая иллюстрация определения предела функции f (x) в точке а изображена на рис. 6.1, из которого следует, что для значений х из некоторой δ-окрестности точки а соответствующие значения f (х) попадают в ε-окрестность точки А.
В данной точке функция может иметь только один конечный или определенного знака бесконечный предел.
Условие существования конечного предела функции в точке дает критерий Коши: для того чтобы функция f (х) имела в точке х = а предел, необходимо и достаточно, чтобы для любого ε > 0 существовала такая проколотая окрестность  точки а, что для любых
точки а, что для любых  и
и  выполнялось бы условие
выполнялось бы условие

Свойства функций, имеющих предел
1. Если функция f (х) имеет в точке х = а предел, то он единственный.
Прежде, чем сформулировать второе свойство, дадим определение ограниченной функции.
Определение. Функция  называется ограниченной на множестве Х, если существует число С > 0, такое, что
называется ограниченной на множестве Х, если существует число С > 0, такое, что  для любых x ÎX.
для любых x ÎX.
Например,  arctg x
arctg x  .
.
2. Функция, имеющая предел в точке, ограничена в некоторой проколотой окрестности этой точки.
3. Если  , то существует такая проколотая окрестность точки х = а, в которой
, то существует такая проколотая окрестность точки х = а, в которой 
4. Если 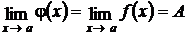 и в некоторой проколотой окрестности этой точки х = а имеет место неравенство
и в некоторой проколотой окрестности этой точки х = а имеет место неравенство  , то
, то  .
.
5. Если определена сложная функция 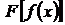 и существуют конечные или бесконечные пределы
и существуют конечные или бесконечные пределы

то существует предел

6. Если  то
то
а) для любых λ и μ существует предел

б) существует предел

в) существует предел
 при
при 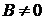 .
.
7. Если С – постоянная величина, то существует предел




 , то, начиная с некоторого номера N, члены последовательности сохраняют знак а.
, то, начиная с некоторого номера N, члены последовательности сохраняют знак а. ,
,  и
и  , то, начиная с некоторого номера N выполняется неравенство
, то, начиная с некоторого номера N выполняется неравенство  .
. , то
, то  .
. выполняются неравенства
выполняются неравенства  и
и  , то
, то  .
. сходятся и
сходятся и  ;
; ;
; ;
; , то
, то  .
. называется неубывающей, если
называется неубывающей, если  . Последовательность называется строго возрастающей, если
. Последовательность называется строго возрастающей, если  . Аналогично, числовая последовательность
. Аналогично, числовая последовательность  называется невозрастающей, если
называется невозрастающей, если  . Последовательность называется строго убывающей, если
. Последовательность называется строго убывающей, если 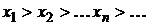 . Возрастающие и убывающие последовательности образуют класс монотонных последовательностей.
. Возрастающие и убывающие последовательности образуют класс монотонных последовательностей. для любого n ∊N и
для любого n ∊N и  монотонная последовательность, а также существует
монотонная последовательность, а также существует 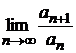 , то:
, то: ; (5.1)
; (5.1) .
. ,
,  .
.
 , то есть
, то есть  . Следовательно, последовательность монотонно убывает. Так как
. Следовательно, последовательность монотонно убывает. Так как  , то согласно формуле (5.1) следует, что
, то согласно формуле (5.1) следует, что  .
. . Согласно неравенству Бернулли,
. Согласно неравенству Бернулли,  ,
,  . Обозначим
. Обозначим  . Тогда для последовательности
. Тогда для последовательности  имеем
имеем  .
.  . Согласно неравенству Бернулли получим
. Согласно неравенству Бернулли получим  . То есть
. То есть  или последовательность
или последовательность  .
.

 ,
, 
 , то функция
, то функция  , определенная равенством F (x) = g(f (x)) называется сложной функцией.
, определенная равенством F (x) = g(f (x)) называется сложной функцией. которое для у ÎY определяет единственный образ f –1(y) = x Î Xназывается обратной функцией или обратным отображением.
которое для у ÎY определяет единственный образ f –1(y) = x Î Xназывается обратной функцией или обратным отображением. y = f(x) – числовая функция одного числового аргумента, например,
y = f(x) – числовая функция одного числового аргумента, например,  и др.
и др. , то
, то  – числовая функция векторного аргумента, или числовая функция многих скалярных переменных, например,
– числовая функция векторного аргумента, или числовая функция многих скалярных переменных, например, 
 – вектор-функция одной переменной, ставящая в соответствие каждому вещественному числу x ÎX вектор
– вектор-функция одной переменной, ставящая в соответствие каждому вещественному числу x ÎX вектор  из
из 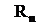 , т.е. каждая координата вектора
, т.е. каждая координата вектора  есть скалярная функция скалярного аргумента х:
есть скалярная функция скалярного аргумента х: .
. , что можно записать в виде
, что можно записать в виде  .
. вектор-функция векторного аргумента. Полагая
вектор-функция векторного аргумента. Полагая  , получим
, получим .
.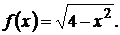



 называется графиком функции
называется графиком функции  . В случае скалярной функции одного скалярного аргумента графиком функции
. В случае скалярной функции одного скалярного аргумента графиком функции  является некоторая поверхность. Например, графиком функции
является некоторая поверхность. Например, графиком функции  является верхняя часть сферы с центром в начале координат радиусом r = 3.
является верхняя часть сферы с центром в начале координат радиусом r = 3. , где α Î R. В общем случае её область определения
, где α Î R. В общем случае её область определения 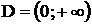 . При
. При  функция
функция  определена на всей числовой оси.
определена на всей числовой оси. , где а > 0, а ≠ 1. Её область определения – вся числовая ось.
, где а > 0, а ≠ 1. Её область определения – вся числовая ось. , где а > 0, а ≠ 1. Область определения
, где а > 0, а ≠ 1. Область определения 
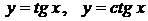 . Функции
. Функции  определены на всей числовой оси. Функция
определены на всей числовой оси. Функция  определена при
определена при 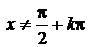 , а
, а  при
при  , где k – любое число.
, где k – любое число.
 y = arctg x, y = arcctg x. Областью определения функций
y = arctg x, y = arcctg x. Областью определения функций 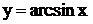 и
и  является отрезок
является отрезок 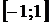 . Функции y = arctg x и y = arcctg x определены на всей числовой оси.
. Функции y = arctg x и y = arcctg x определены на всей числовой оси. гиперболический синус,
гиперболический синус,  гиперболический косинус (
гиперболический косинус ( натуральное число [3.4]),
натуральное число [3.4]),  гиперболический тангенс,
гиперболический тангенс, 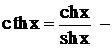 гиперболический котангенс.
гиперболический котангенс. x ∊D(f) всегда
x ∊D(f) всегда  (монотонно убывающие, если для любых
(монотонно убывающие, если для любых  ).
). (для нечётных функций
(для нечётных функций 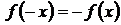 ).
). и x + Т ∊D(f) выполняются равенства:
и x + Т ∊D(f) выполняются равенства:  . Т называется периодом.
. Т называется периодом. К ∊ R (для функций ограниченных снизу
К ∊ R (для функций ограниченных снизу  ).
). < δ выполняется неравенство
< δ выполняется неравенство 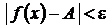 . Пишут
. Пишут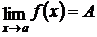 .
. , если для любого ε > 0 существует число М(ε) > 0 такое, что при x >M(ε) выполняется неравенство
, если для любого ε > 0 существует число М(ε) > 0 такое, что при x >M(ε) выполняется неравенство  .
. (левосторонний предел).
(левосторонний предел). (правосторонний предел).
(правосторонний предел). Геометрическая иллюстрация определения предела функции f (x) в точке а изображена на рис. 6.1, из которого следует, что для значений х из некоторой δ-окрестности точки а соответствующие значения f (х) попадают в ε-окрестность точки А.
Геометрическая иллюстрация определения предела функции f (x) в точке а изображена на рис. 6.1, из которого следует, что для значений х из некоторой δ-окрестности точки а соответствующие значения f (х) попадают в ε-окрестность точки А. точки а, что для любых
точки а, что для любых  и
и  выполнялось бы условие
выполнялось бы условие
 называется ограниченной на множестве Х, если существует число С > 0, такое, что
называется ограниченной на множестве Х, если существует число С > 0, такое, что  для любых x ÎX.
для любых x ÎX. arctg x
arctg x  .
. , то существует такая проколотая окрестность точки х = а, в которой
, то существует такая проколотая окрестность точки х = а, в которой 
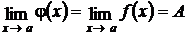 и в некоторой проколотой окрестности этой точки х = а имеет место неравенство
и в некоторой проколотой окрестности этой точки х = а имеет место неравенство  , то
, то  .
.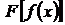 и существуют конечные или бесконечные пределы
и существуют конечные или бесконечные пределы

 то
то

 при
при 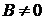 .
.



