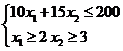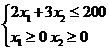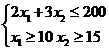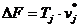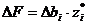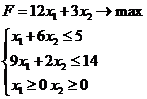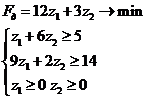Оптимальные решения исходной и двойственной задач связаны соотношениями:
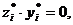
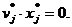
Эта теорема означает, что между переменными исходной и двойственной задач существует взаимосвязь, которая заключается в том, что одна переменная из пары должна быть нулевой.
Рассмотрим связь между 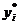 (остаток ресурса i-го вида) и
(остаток ресурса i-го вида) и 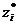 (теневая цена ресурса i-го вида).
(теневая цена ресурса i-го вида).
Если 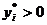 , то имеется остаток ресурса i -го вида, т.е. ресурс не дефицитен. Увеличение количества этого ресурса не вызовет увеличение прибыли, а только увеличится его остаток. Поэтому соответствующая теневая цена должна быть равна нулю:
, то имеется остаток ресурса i -го вида, т.е. ресурс не дефицитен. Увеличение количества этого ресурса не вызовет увеличение прибыли, а только увеличится его остаток. Поэтому соответствующая теневая цена должна быть равна нулю: 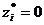 .
.
Если 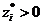 , то i -й ресурс является дефицитным, поскольку при его увеличении прибыль растет. Следовательно, он был использован полностью, т.е. остатка нет:
, то i -й ресурс является дефицитным, поскольку при его увеличении прибыль растет. Следовательно, он был использован полностью, т.е. остатка нет: 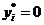 .
.
Рассмотрим теперь связь между  (оптимальный объем производства продукции j-го типа) и
(оптимальный объем производства продукции j-го типа) и  (потери при производстве единицы продукции j-го типа).
(потери при производстве единицы продукции j-го типа).
Если 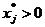 , то этот вид продукции согласно оптимальному плану должен быть произведен в каком-то количестве. Следовательно, он является выгодным. Поэтому соответствующие потери равны нулю:
, то этот вид продукции согласно оптимальному плану должен быть произведен в каком-то количестве. Следовательно, он является выгодным. Поэтому соответствующие потери равны нулю:  .
.
Если 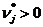 , то данный вид продукции не является выгодным, поэтому в оптимальный план он не войдет:
, то данный вид продукции не является выгодным, поэтому в оптимальный план он не войдет:  .
.
6.3.7 Пример анализа отчетов для задачи планирования производства продукции
Для производства продукции четырех типов Прод1, Прод2, Прод3 и Прод4 требуются ресурсы трех видов: трудовые, сырье, финансы. Нормы расхода ресурсов и другие исходные данные приведены в таблице 6.3.
Таблица 6.3 - Исходные данные к задаче планирования производства продукции
| Ресурсы
| Прод1
| Прод2
| Прод3
| Прод4
| Наличие ресурса
|
| Трудовые, чел.-ч
|
|
|
|
|
|
| Сырье, кг
|
|
|
|
|
|
| Финансы, тыс.р.
|
|
|
|
|
|
| Прибыль, ден.ед.
|
|
|
|
|
|
Найти оптимальный план производства продукции, а также дать ответ на следующие вопросы:
1. Какие типы продукции вошли в оптимальный план производства? Какова максимальная прибыль?
2. Какие ресурсы при этом израсходованы полностью, а какие нет?
3. Какая продукция является выгодной, а какая – нет? Какая продукция является наиболее невыгодной? Как изменится общая прибыль, если придется выпускать 1 или 3 единицы этой продукции?
4. Какой ресурс является наиболее дефицитным? Насколько увеличится общая прибыль, если количество наиболее дефицитного ресурса увеличить на 1, а также 3 и 5 единиц?
5. Прибыль от продажи единицы продукции в принципе может измениться (например, под влиянием конкурентов). Как повлияет на оптимальное решение ситуация, когда прибыль от единицы продукции третьего типа уменьшится на 10 ден.ед. (т.е. составит не 120, а 110 ден.ед.)? А если уменьшение прибыли составит 15 ден. ед.?
6. Покажите выполнение второй теоремы двойственности.
7. Предприятию предлагают начать выпуск нового (пятого) вида изделия, нормы затрат на одну единицу которого равны 2 чел.-ч. трудовых ресурсов, 5 кг сырья, 3 тыс. р. финансов, а прибыль составляет 65 ден. ед. за единицу. Целесообразно ли введение в план производства предприятия этой продукции?
Решение. Составим математическую модель этой задачи. Для этого выполним три шага:
1. Введем переменные. Нужно найти план производства, т.е. количество продукции каждого вида, которые следует производить. Таким образом, будет 4 переменных:
x1 - количество продукции 1 вида;
x2 –количество продукции 2 вида;
x3 –количество продукции 3 вида;
x4 –количество продукции 4 вида.
2. Запишем целевую функцию. Она должна выражать собой критерий оптимальности (т.е. тот показатель, который в задаче должен достигнуть максимума или минимума). В нашей задаче указано, что должна быть максимальна прибыль. Поэтому целевая функция должна представлять собой формулу расчета прибыли. Прибыль от единицы продукции первого типа составляет 60 денежных единиц, а поскольку мы собираемся выпускать x1 таких изделий, прибыль от них составит 60x1 ден. ед. Аналогично прибыль от продукции второго типа равна 70x2 ден. ед., и т.д. Общая прибыль от всей продукции равна сумме:
F=60x1+70x2+120x3+130x4 → max
3. Запишем систему ограничений. Очевидно, что расход каждого вида ресурса не должен превышать его запас. Расход трудовых ресурсов на продукцию первого типа равен 1x1, на продукцию второго типа – 1x2, и т.д. Общий расход трудовых ресурсов выражается с помощью формулы: х1+х2+х3+х4, а запас равен 16. Поэтому имеем неравенство:
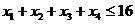 .
.
Аналогично записываются другие ограничения. Кроме того, здравый смысл требует, чтобы количество производимой продукции было величиной неотрицательной. Таким образом, модель задачи имеет вид:
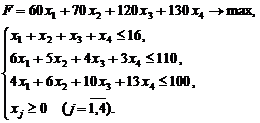
Приведем исходную задачу к каноническому виду, введя дополнительные переменные:
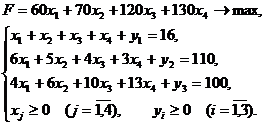
Дополнительные переменные yi – это остатки ресурсов каждого вида. Т.е. y1 – это остаток трудовых ресурсов, y2 – остаток сырья, а y3 – остаток финансов.
Составим двойственную задачу, используя формальные правила составления двойственных задач:
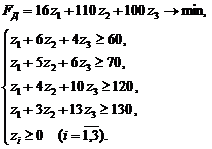
Экономический смысл этой задачи вытекает из предположения о том, что все ресурсы можно продать некоторой сторонней организации вместо того, чтобы производить собственную продукцию. Тогда двойственные переменные zi - это оценки ресурсов задачи (цена единицы каждого ресурса). Целевая функция задачи представляет собой общую стоимость ресурсов, которую покупающая организации стремится уменьшить. Ограничения выражают условия продающего ресурсы предприятия, которое хочет получить за них не меньше чем, если бы само производило продукцию. Например, предприятие откажется от выпуска продукции первого типа при условии, что стоимость всех ресурсов, которые будут потрачены на выпуск единицы этой продукции (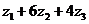 ) будет не менее, чем прибыль от производства готовой единицы продукции (60).
) будет не менее, чем прибыль от производства готовой единицы продукции (60).
В двойственной задаче приведем ограничения к виду равенства, вычитая из левых частей ограничений дополнительные переменные:
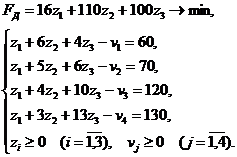
Дополнительные двойственные переменные vj есть потери при производстве единицы продукции j -го типа. Т.е эти переменные означают разность между той суммой, что можно было бы получить при продаже ресурсов, и прибылью, получаемой при производстве самой продукции (например, для продукции первого типа 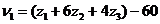 ). Т.е. это величина показывает, насколько выгоднее было бы продать ресурсы, чем производить данный тип продукции.
). Т.е. это величина показывает, насколько выгоднее было бы продать ресурсы, чем производить данный тип продукции.
Решим исходную задачу с помощью надстройки MS Excel «Поиск решения».
Исходные данные должны быть представлены в виде таблицы, которая содержит формулы вычисления целевой функции, левых и правых частей ограничений. Ячейки, которые отведены под значения переменных, называются изменяемыми. В них должны быть введены начальные приближения для переменных (например, нулевые). Когда надстройка “Поиск решения” закончит вычисления, в эти ячейки будут записаны найденные оптимальные значения переменных.
Ячейка, которая содержит формулу вычисления значения целевой функции, называется целевой.
1 шаг. Подготовка исходных данных задачи на листе Excel. Исходные данные для надстройки «Поиск решения» могут быть подготовлены, как показано на рисунке 6.1.
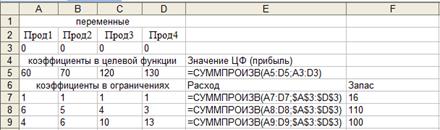
Рисунок 6.1 – Лист Excel с исходными данными и формулами для решения задачи с помощью надстройки «Поиск решения»
Изменяемыми ячейками будут ячейки A3:D3, которые отведены под значения переменных. В них введены начальные значения переменных (нулевые).
Целевой ячейкой будет являться ячейка Е5, которая содержит формулу вычисления значения целевой функции (т.е, прибыли от продажи готовой продукции). При большом числе переменных эту формулу удобно задавать с помощью стандартной функции Excel СУММПРОИЗВ(). Для облегчения её ввода применяется мастер функций, вызываемый кнопкой  . Данная функция относится к категории Математические. Выбрав ее название в меню, нужно заполнить окно параметров. При этом Массив 1 – это диапазон коэффициентов целевой функциии, а Массив 2 – диапазон изменяемых ячеек (в нашем примере A3:D3). Функция СУММПРОИЗВ() соответствующие ячейки диапазонов перемножает и находит сумму этих произведений. Например, формула в ячейке Е5 записана в виде CУММПРОИЗВ(A5:D5;A3:D3), что соответствует формуле расчета прибыли 60x1+70x2+120x3+130x4.
. Данная функция относится к категории Математические. Выбрав ее название в меню, нужно заполнить окно параметров. При этом Массив 1 – это диапазон коэффициентов целевой функциии, а Массив 2 – диапазон изменяемых ячеек (в нашем примере A3:D3). Функция СУММПРОИЗВ() соответствующие ячейки диапазонов перемножает и находит сумму этих произведений. Например, формула в ячейке Е5 записана в виде CУММПРОИЗВ(A5:D5;A3:D3), что соответствует формуле расчета прибыли 60x1+70x2+120x3+130x4.
В ячейки E7:E9 введены формулы вычисления левых частей ограничений (расход ресурса каждого вида). Они также заданы с помощью функции СУММПРОИЗВ(). При этом на изменяемые ячейки поставлены абсолютные ссылки (знаки $). Для этого при вводе параметров функции, выделив диапазон изменяемых ячеек, нужно нажать клавишу F4. Абсолютные ссылки не изменяются при копировании формулы. Поэтому, если навести курсор на правый нижний угол ячейки E7 и, нажав левую кнопку мыши, протянуть вниз (скопировать методом автозаполнения), то формулы будут скопированы правильно. Изменятся коэффициенты в ограничениях, а ссылки на изменяемые ячейки останутся теми же. Если не использовать копирование формулы, а вводить функцию СУММПРОИЗВ() в каждую ячейку заново, то абсолютные ссылки не нужны.
2 шаг. Вызов надстройки «Поиск решения» выполняется командой Сервис/Поиск решения. Если этого пункта нет в меню, то следует загрузить надстройку командой Сервис/Надстройки и в окне диалога Надстройки установить флажок в строке «Поиск решения».
3 шаг. Задание условий поиска. В окне «Поиск решения» следует указать адрес целевой ячейки и цель, которая должна быть достигнута (максимальное или минимальное значение целевой функции), адреса изменяемых ячеек (в которых «Поиск решения» должен подобрать значения), а также задать ограничения задачи. Пример заполнения полей окна «Поиск решения» показан на рисунке 6.2.
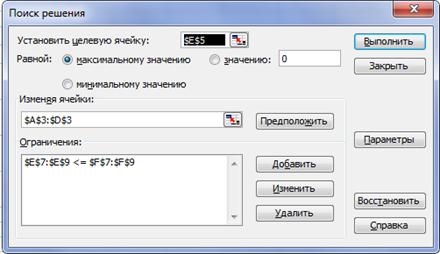
Рисунок 6.2 – Окно «Поиск решения» для задачи планирования производства продукции
Для ввода ограничений нужно нажать кнопку Добавить. Появляется окно «Добавление ограничений» (рисунок 6.3). В поле Ссылка на ячейку указывается ячейка, содержащая формулу левой части ограничения. Затем из раскрывающегося списка можно выбрать знак ограничения. В поле Ограничение указывается ячейка, содержащая правую часть ограничения, или непосредственно его числовое значение. После ввода первого ограничения следует нажать кнопку Добавить, т.к. ввод еще не закончен. После ввода последнего ограничения нужно нажать кнопку ОК и вернуться в окно “Поиск решения”.
Поскольку все ограничения по ресурсам имеют одинаковый знак, то их можно задать одновременно: E7:E9<=F7:F9. C помощью кнопок Добавить, Изменить, Удалить в окне “Поиск решения” можно редактировать введенное ограничение.
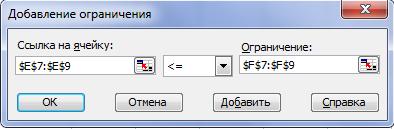
Рисунок 6.3 – Окно «Добавление ограничения»
4 шаг. Задание параметров поиска. Нажав кнопку Параметры, можно установить параметры алгоритма поиска (рисунок 6.4).
В данном примере нужно все параметры оставить по умолчанию, установить только два флажка:
§ флажок Линейная модель, который указывает, что это задача линейного программирования и позволяет получать в дальнейшем правильные отчеты;
§ флажок Неотрицательные значения, который задает условия неотрицательности переменных, которые учтены в математической модели задачи.
После установки флажков нужно нажать кнопку OK, чтобы вернуться в окно ”Поиск решения”.
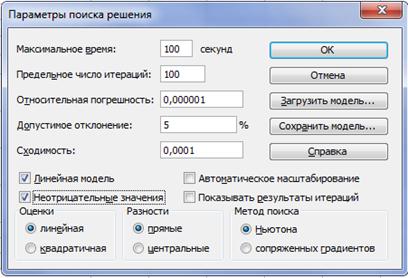
Рисунок 6.4 – Окно «Параметры поиска решения»
5 шаг. Запуск процесса решения. Нажатие кнопки Выполнить активизирует процесс поиска решения. В процессе поиска его отдельные шаги будут отображаться в строке состояния. По окончании поиска на экране появляется окно «Результаты поиска решения» (рисунок 6.5).
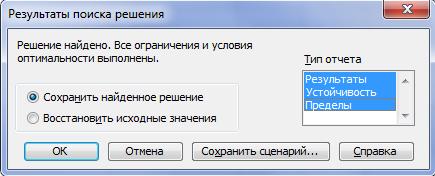
Рисунок 6.5 – Окно «Результаты поиска решения»
Если задача успешно решена, то в этом окне появляется сообщение «Решение найдено. Все ограничения и условия оптимальности выполнены». Нужно переключатель установить в положение Сохранить найденное решение, в списке «Тип отчета» выделить все названия отчетов (используя клавишу Shift или Ctrl), а затем нажать кнопку OK. На листе Excel с условием задачи будет зафиксирован результат решения (изменяемые ячейки получат оптимальные значения, а также изменится результат в ячейках с формулами), а на отдельных листах будут сформированы отчеты по результатам, по устойчивости и по пределам.
Если же в окне «Результаты поиска решения» показано другое сообщение, то это означает ошибку в математической модели или в процессе решения в Excel. Список «Тип отчета» в этом случае будет недоступен. Следует поставить переключатель в положение Восстановить исходные значения, нажать OK, и заняться поиском ошибки.
6 шаг. Интерпретация результатов решения. Лист Excel с результатами решения показан на рисунке 6.6. Из него следует, что оптимальные значения переменных следующие:  =10,
=10,  =0,
=0, 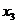 =6,
=6, 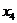 =0. Максимальное значение целевой функции (прибыль) составит
=0. Максимальное значение целевой функции (прибыль) составит 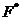 =1320 денежных единиц.
=1320 денежных единиц.
Отчет по результатам показан на рисунке 6.7. В нем содержится та же информация, что и на листе с решением задачи. Т.е., из этого отчета можно было также получить оптимальные значения переменных 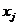 и значение целевой функции. Кроме того, в графе «Разница» показаны остатки неиспользованных ресурсов. Таким образом, можно выписать значения дополнительных переменных:
и значение целевой функции. Кроме того, в графе «Разница» показаны остатки неиспользованных ресурсов. Таким образом, можно выписать значения дополнительных переменных:  .
.
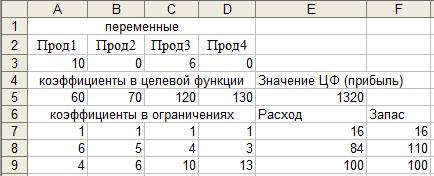
Рисунок 6.6 – Результаты решения задачи планирования производства продукции

Рисунок 6.7 – Отчет по результатам
Отчет по устойчивости представлен на рисунке 6.8. Из него можно выписать оптимальные значения двойственных переменных. Оценки ресурсов содержатся в графе «Теневая цена». Т.е.,  z1*=20; z2*=0; z3*=10. Из графы «Нормированная стоимость» можно выписать оптимальные значения дополнительных двойственных переменных:
z1*=20; z2*=0; z3*=10. Из графы «Нормированная стоимость» можно выписать оптимальные значения дополнительных двойственных переменных: 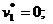
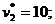
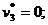
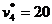 .
.
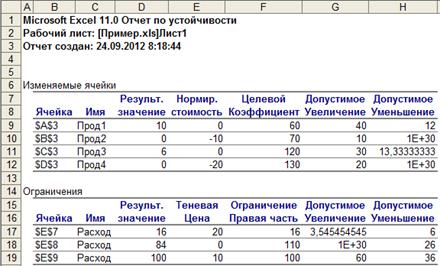
Рисунок 6. 8 – Отчет по устойчивости
Ответы на вопросы задания:
1. В оптимальный план производства входит продукция первого типа в количестве 10 единиц ( ) и продукция третьего типа в количестве 6 единиц (
) и продукция третьего типа в количестве 6 единиц (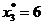 ). Вторую и четвертую продукцию производить невыгодно (
). Вторую и четвертую продукцию производить невыгодно (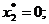
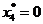 ). При этом будет достигнута максимальная прибыль в количестве 1320 ден. ед. (F* =1320).
). При этом будет достигнута максимальная прибыль в количестве 1320 ден. ед. (F* =1320).
2. При оптимальном плане производства трудовые ресурсы и финансы будут использованы полностью ( ), а сырья будет остаток в 26 единиц
), а сырья будет остаток в 26 единиц 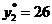 .
.
3. Для продукции первого и третьего типа значение потерь при производстве равно нулю (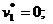
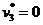 ), следовательно, эта продукция является выгодной. Вторая и четвертая продукция имеет положительные потери при производстве (т.е. для нее выгоднее продавать ресурсы, а не готовую продукцию).
), следовательно, эта продукция является выгодной. Вторая и четвертая продукция имеет положительные потери при производстве (т.е. для нее выгоднее продавать ресурсы, а не готовую продукцию).
Наиболее невыгодной в данном примере является продукция четвертого типа, т.к. ее нормированная стоимость наибольшая (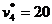 ). При выпуске единицы этой продукции общая прибыль уменьшается на 20 единиц, согласно свойству нормированной стоимости. При выпуске трех единиц этой продукции уменьшение прибыли составит
). При выпуске единицы этой продукции общая прибыль уменьшается на 20 единиц, согласно свойству нормированной стоимости. При выпуске трех единиц этой продукции уменьшение прибыли составит 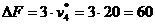 денежных единиц.
денежных единиц.
4. Наиболее дефицитным видом ресурсов в данном примере являются трудовые ресурсы, поскольку их теневая цена наибольшая (z1*=20). Согласно теореме об оценках, если количество трудовых ресурсов увеличить на 1, то общая прибыль возрастет на 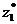 =20 единиц. Увеличение трудовых ресурсов на 3 единицы дает увеличение прибыли на DF=3×
=20 единиц. Увеличение трудовых ресурсов на 3 единицы дает увеличение прибыли на DF=3× 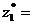 3×20=60 единиц, если структура решения при этом не изменится. Из отчета по устойчивости допустимое увеличение количества трудовых ресурсов
3×20=60 единиц, если структура решения при этом не изменится. Из отчета по устойчивости допустимое увеличение количества трудовых ресурсов 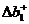 = 3,55; допустимое уменьшение
= 3,55; допустимое уменьшение 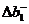 =6. Это означает, что структура решения не изменяется, если
=6. Это означает, что структура решения не изменяется, если
16-6 ≤ b1 ≤ 16+3,55, т.е. 10 ≤ b1 ≤ 19,55.
Поэтому, если количество трудовых ресурсов возрастет на 5 единиц, теорема об оценках перестанет действовать, и мы не можем количественно измерить увеличение прибыли.
5. Согласно отчету по устойчивости (рисунок 6.8) допустимое уменьшение целевого коэффициента для переменной x3 составляет 13,3. Это означает, что если прибыль от производства и продажи продукции типа 3 уменьшится более чем на эту величину, то оптимальный план изменится. Поэтому, при уменьшении прибыли на 10 ден. ед. оптимальный план останется тем же: 10 единиц продукции №1 и 6 единиц продукции №3. Если же прибыль уменьшится на 15 ден.ед, то произойдет выход за пределы устойчивости, и оптимальный план поменяется. Как именно – без повторного решения неизвестно. Скорее всего, продукция третьего типа станет относительно невыгодной.
6. Соотношение 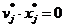 выполняется для всех видов продукции. Продукция второго и четвертого типа имеет положительную нормированную стоимость (
выполняется для всех видов продукции. Продукция второго и четвертого типа имеет положительную нормированную стоимость (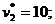
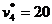 ), т.е. невыгодна относительно других видов продукции, поэтому она не вошла в оптимальный план (
), т.е. невыгодна относительно других видов продукции, поэтому она не вошла в оптимальный план (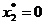 и
и 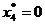 ). Продукция первого и третьего типа вошла в оптимальный план производства (
). Продукция первого и третьего типа вошла в оптимальный план производства (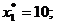
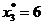 ) поскольку является выгодной (
) поскольку является выгодной (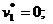
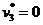 ).
).
Для сырья, которое имеется в остатке (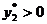 ), теневая цена равна нулю. А для трудовых ресурсов и финансов, которые использованы полностью (т.е.
), теневая цена равна нулю. А для трудовых ресурсов и финансов, которые использованы полностью (т.е. 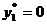 и
и  ) теневые цены положительны. Т.е. соотношение
) теневые цены положительны. Т.е. соотношение 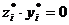 второй теоремы двойственности также выполняется.
второй теоремы двойственности также выполняется.
7. Продукция будет невыгодной и не войдет в план производства в том случае если соответствующая нормированная стоимость окажется больше 0, т.е. оценка ресурсов, которые идут на производство единицы этой продукции, окажется больше прибыли от этой продукции. Учитывая значения теневых цен ресурсов, полученных в отчете по устойчивости  z1*=20; z2*=0; z3*=10, найдем оценку всех ресурсов, которые будут потрачены на производство нового вида продукции:
z1*=20; z2*=0; z3*=10, найдем оценку всех ресурсов, которые будут потрачены на производство нового вида продукции: 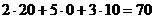 . Эта оценка больше прибыли от данной продукции (65 ден. ед.), поэтому ее невыгодно вводить в план производства (
. Эта оценка больше прибыли от данной продукции (65 ден. ед.), поэтому ее невыгодно вводить в план производства (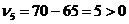 ).
).
Примеры тестовых заданий по теме 6
1. Целевая функция задачи линейного программирования выражает:
a) наилучшие значения переменных
b) количество израсходованных ресурсов
c) критерий оптимальности
d) максимальную прибыль при минимальных затратах
Ответ: c). Целевая функция выражает критерий оптимальности, т.е. показатель, который служит для выбора оптимального решения. Ответ d) неверен, т.к. должно быть только одно значение целевой функции (либо максимальная прибыль, либо минимальные затраты).
2. Дана следующая задача линейного программирования: «Предприятие может выпускать изделия двух видов, которые продаются по ценам соответственно 10 у.е. и 15 у.е. за штуку. Сырья для производства продукции имеется 200 кг. На производство изделия первого вида затрачивается 2 кг сырья, второго вида – 3 кг. Найти оптимальную производственную программу выпуска изделий, которая обеспечивает предприятию максимальную выручку. Выберите правильный вариант системы ограничений:
a) 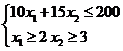
b) 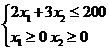
с) 
d) 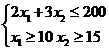
Ответ: b)
3. Выберите верный вариант формулировки теоремы об оценках:
a) 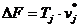
b) 
c) 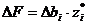
d) max F=min FД
Ответ: c).
5. Дана задача линейного программирования:
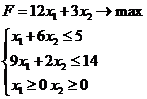
Какой вариант двойственной задачи ей соответствует?
a) 
b) 
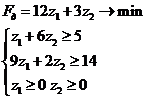
c) 
Ответ: a)





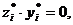
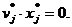
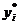 (остаток ресурса i-го вида) и
(остаток ресурса i-го вида) и 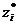 (теневая цена ресурса i-го вида).
(теневая цена ресурса i-го вида).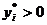 , то имеется остаток ресурса i -го вида, т.е. ресурс не дефицитен. Увеличение количества этого ресурса не вызовет увеличение прибыли, а только увеличится его остаток. Поэтому соответствующая теневая цена должна быть равна нулю:
, то имеется остаток ресурса i -го вида, т.е. ресурс не дефицитен. Увеличение количества этого ресурса не вызовет увеличение прибыли, а только увеличится его остаток. Поэтому соответствующая теневая цена должна быть равна нулю: 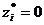 .
.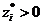 , то i -й ресурс является дефицитным, поскольку при его увеличении прибыль растет. Следовательно, он был использован полностью, т.е. остатка нет:
, то i -й ресурс является дефицитным, поскольку при его увеличении прибыль растет. Следовательно, он был использован полностью, т.е. остатка нет: 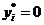 .
. (оптимальный объем производства продукции j-го типа) и
(оптимальный объем производства продукции j-го типа) и  (потери при производстве единицы продукции j-го типа).
(потери при производстве единицы продукции j-го типа).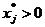 , то этот вид продукции согласно оптимальному плану должен быть произведен в каком-то количестве. Следовательно, он является выгодным. Поэтому соответствующие потери равны нулю:
, то этот вид продукции согласно оптимальному плану должен быть произведен в каком-то количестве. Следовательно, он является выгодным. Поэтому соответствующие потери равны нулю:  .
.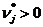 , то данный вид продукции не является выгодным, поэтому в оптимальный план он не войдет:
, то данный вид продукции не является выгодным, поэтому в оптимальный план он не войдет:  .
.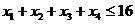 .
.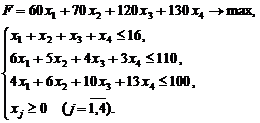
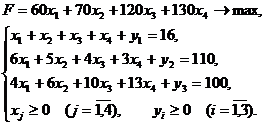
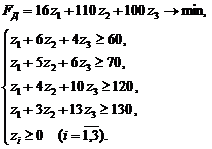
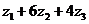 ) будет не менее, чем прибыль от производства готовой единицы продукции (60).
) будет не менее, чем прибыль от производства готовой единицы продукции (60).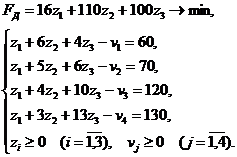
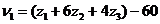 ). Т.е. это величина показывает, насколько выгоднее было бы продать ресурсы, чем производить данный тип продукции.
). Т.е. это величина показывает, насколько выгоднее было бы продать ресурсы, чем производить данный тип продукции.
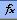 . Данная функция относится к категории Математические. Выбрав ее название в меню, нужно заполнить окно параметров. При этом Массив 1 – это диапазон коэффициентов целевой функциии, а Массив 2 – диапазон изменяемых ячеек (в нашем примере A3:D3). Функция СУММПРОИЗВ() соответствующие ячейки диапазонов перемножает и находит сумму этих произведений. Например, формула в ячейке Е5 записана в виде CУММПРОИЗВ(A5:D5;A3:D3), что соответствует формуле расчета прибыли 60x1+70x2+120x3+130x4.
. Данная функция относится к категории Математические. Выбрав ее название в меню, нужно заполнить окно параметров. При этом Массив 1 – это диапазон коэффициентов целевой функциии, а Массив 2 – диапазон изменяемых ячеек (в нашем примере A3:D3). Функция СУММПРОИЗВ() соответствующие ячейки диапазонов перемножает и находит сумму этих произведений. Например, формула в ячейке Е5 записана в виде CУММПРОИЗВ(A5:D5;A3:D3), что соответствует формуле расчета прибыли 60x1+70x2+120x3+130x4.



 =10,
=10,  =0,
=0, 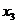 =6,
=6, 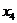 =0. Максимальное значение целевой функции (прибыль) составит
=0. Максимальное значение целевой функции (прибыль) составит 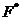 =1320 денежных единиц.
=1320 денежных единиц.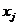 и значение целевой функции. Кроме того, в графе «Разница» показаны остатки неиспользованных ресурсов. Таким образом, можно выписать значения дополнительных переменных:
и значение целевой функции. Кроме того, в графе «Разница» показаны остатки неиспользованных ресурсов. Таким образом, можно выписать значения дополнительных переменных:  .
.

 z1*=20; z2*=0; z3*=10. Из графы «Нормированная стоимость» можно выписать оптимальные значения дополнительных двойственных переменных:
z1*=20; z2*=0; z3*=10. Из графы «Нормированная стоимость» можно выписать оптимальные значения дополнительных двойственных переменных: 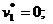
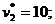
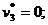
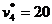 .
.
 ) и продукция третьего типа в количестве 6 единиц (
) и продукция третьего типа в количестве 6 единиц (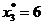 ). Вторую и четвертую продукцию производить невыгодно (
). Вторую и четвертую продукцию производить невыгодно (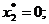
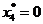 ). При этом будет достигнута максимальная прибыль в количестве 1320 ден. ед. (F* =1320).
). При этом будет достигнута максимальная прибыль в количестве 1320 ден. ед. (F* =1320). ), а сырья будет остаток в 26 единиц
), а сырья будет остаток в 26 единиц 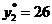 .
.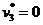 ), следовательно, эта продукция является выгодной. Вторая и четвертая продукция имеет положительные потери при производстве (т.е. для нее выгоднее продавать ресурсы, а не готовую продукцию).
), следовательно, эта продукция является выгодной. Вторая и четвертая продукция имеет положительные потери при производстве (т.е. для нее выгоднее продавать ресурсы, а не готовую продукцию).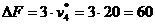 денежных единиц.
денежных единиц.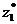 =20 единиц. Увеличение трудовых ресурсов на 3 единицы дает увеличение прибыли на DF=3×
=20 единиц. Увеличение трудовых ресурсов на 3 единицы дает увеличение прибыли на DF=3× 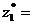 3×20=60 единиц, если структура решения при этом не изменится. Из отчета по устойчивости допустимое увеличение количества трудовых ресурсов
3×20=60 единиц, если структура решения при этом не изменится. Из отчета по устойчивости допустимое увеличение количества трудовых ресурсов 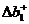 = 3,55; допустимое уменьшение
= 3,55; допустимое уменьшение 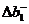 =6. Это означает, что структура решения не изменяется, если
=6. Это означает, что структура решения не изменяется, если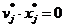 выполняется для всех видов продукции. Продукция второго и четвертого типа имеет положительную нормированную стоимость (
выполняется для всех видов продукции. Продукция второго и четвертого типа имеет положительную нормированную стоимость (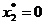 и
и 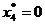 ). Продукция первого и третьего типа вошла в оптимальный план производства (
). Продукция первого и третьего типа вошла в оптимальный план производства (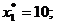
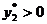 ), теневая цена равна нулю. А для трудовых ресурсов и финансов, которые использованы полностью (т.е.
), теневая цена равна нулю. А для трудовых ресурсов и финансов, которые использованы полностью (т.е. 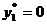 и
и  ) теневые цены положительны. Т.е. соотношение
) теневые цены положительны. Т.е. соотношение 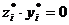 второй теоремы двойственности также выполняется.
второй теоремы двойственности также выполняется.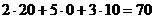 . Эта оценка больше прибыли от данной продукции (65 ден. ед.), поэтому ее невыгодно вводить в план производства (
. Эта оценка больше прибыли от данной продукции (65 ден. ед.), поэтому ее невыгодно вводить в план производства (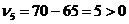 ).
).