6.3.1 Постановка задачи планирования производства продукции
Рассмотрим частный случай задачи линейного программирования – задачу планирования производства продукции.
Для производства продукции n типов требуются ресурсы m видов. Нормы расхода ресурсов на производство единицы продукции каждого типа заданы матрицей  , где
, где  – количество ресурса i–го вида, необходимое для производства единицы продукции j-го типа. Известно количество ресурсов
– количество ресурса i–го вида, необходимое для производства единицы продукции j-го типа. Известно количество ресурсов  (
( ) каждого вида, которое имеется в наличии у предприятия. Известны также величины прибыли Сj (
) каждого вида, которое имеется в наличии у предприятия. Известны также величины прибыли Сj ( ), которую получит предприятие при реализации единицы продукции j-го типа. Требуется найти оптимальный план производства продукции, т.е. количество продукции каждого типа, которое нужно произвести, чтобы получить наибольшую прибыль. Условие задачи можно представить в виде таблицы 6.1.
), которую получит предприятие при реализации единицы продукции j-го типа. Требуется найти оптимальный план производства продукции, т.е. количество продукции каждого типа, которое нужно произвести, чтобы получить наибольшую прибыль. Условие задачи можно представить в виде таблицы 6.1.
Таблица 6.1. - Исходные данные к задаче планирования производства продукции
| Ресурсы
| Продукция
| Наличие
ресурсов
|
| Тип 1
| Тип 2
| …
| Тип n
|
| Ресурс 1
| a11
| a12
| …
| a1n
| b1
|
| Ресурс 2
| a21
| a22
| …
| a2n
| b2
|
| …
| …
| …
| …
| …
| …
|
| Ресурс m
| am1
| am2
| …
| amn
| bm
|
| Прибыль
| C1
| C2
| …
| Cn
|
|
Обозначим через xj – количество продукции j-го типа, которое планируется выпустить ( ). Тогда математическая модель задачи будет выглядеть следующим образом:
). Тогда математическая модель задачи будет выглядеть следующим образом:
 (6.1)
(6.1)
 (6.2)
(6.2)
 (6.3)
(6.3)
Целевая функция (6.1) этой задачи представляет собой общую прибыль от производства всей продукции. Ограничения (6.2) выражают условие того, что потребление ресурса i-го вида не должно превышать запаса этого ресурса. Условия неотрицательности переменных (6.3) вытекают из смысла переменной x j ( ): количество продукции не может быть отрицательным.
): количество продукции не может быть отрицательным.
Каноническая форма записи ЗЛП
Канонической называется форма записи ЗЛП, в которой целевая функция стремится к максимуму, все ограничении имеют вид равенства и на все переменные наложено условие неотрицательности.
Чтобы привести к каноническому виду задачу с ограничениями-неравенствами, вводят дополнительные переменные. Причем если неравенство имеет вид “меньше или равно”(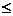 ), то дополнительную переменную прибавляют к левой части ограничения, а если вид “больше или равно”(
), то дополнительную переменную прибавляют к левой части ограничения, а если вид “больше или равно”( ), то дополнительную переменную вычитают из его левой части. В целевую функцию дополнительные переменные вводят с коэффициентами, равными 0.
), то дополнительную переменную вычитают из его левой части. В целевую функцию дополнительные переменные вводят с коэффициентами, равными 0.
Таким образом, задача (6.1) – (6.3) может быть записана в следующей канонической форме:

 (6.4)
(6.4)


Дополнительные переменные yi ( ) представляют собой остатки ресурсов каждого вида. Если в оптимальном решении какой-либо ресурс будет использован полностью, то ограничение исходной задачи (6.2) будет выполнено в виде равенства и yi=0. Такое ограничение в отчетах Exсel называется связанным. Ресурс, который использован полностью, считается дефицитным.
) представляют собой остатки ресурсов каждого вида. Если в оптимальном решении какой-либо ресурс будет использован полностью, то ограничение исходной задачи (6.2) будет выполнено в виде равенства и yi=0. Такое ограничение в отчетах Exсel называется связанным. Ресурс, который использован полностью, считается дефицитным.



 , где
, где  – количество ресурса i–го вида, необходимое для производства единицы продукции j-го типа. Известно количество ресурсов
– количество ресурса i–го вида, необходимое для производства единицы продукции j-го типа. Известно количество ресурсов  (
( ) каждого вида, которое имеется в наличии у предприятия. Известны также величины прибыли Сj (
) каждого вида, которое имеется в наличии у предприятия. Известны также величины прибыли Сj ( ), которую получит предприятие при реализации единицы продукции j-го типа. Требуется найти оптимальный план производства продукции, т.е. количество продукции каждого типа, которое нужно произвести, чтобы получить наибольшую прибыль. Условие задачи можно представить в виде таблицы 6.1.
), которую получит предприятие при реализации единицы продукции j-го типа. Требуется найти оптимальный план производства продукции, т.е. количество продукции каждого типа, которое нужно произвести, чтобы получить наибольшую прибыль. Условие задачи можно представить в виде таблицы 6.1. (6.1)
(6.1) (6.2)
(6.2) (6.3)
(6.3)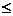 ), то дополнительную переменную прибавляют к левой части ограничения, а если вид “больше или равно”(
), то дополнительную переменную прибавляют к левой части ограничения, а если вид “больше или равно”( ), то дополнительную переменную вычитают из его левой части. В целевую функцию дополнительные переменные вводят с коэффициентами, равными 0.
), то дополнительную переменную вычитают из его левой части. В целевую функцию дополнительные переменные вводят с коэффициентами, равными 0.
 (6.4)
(6.4)




